基于非参数核密度估计与Copula方法的山东省小麦收入保险定价研究
2019-10-19
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
科学厘定农作物收入保险费率,对分散农业生产风险、促进农业可持续发展具有重要意义。收入保险费率厘定的关键在于两个方面:一是对单产风险、价格风险的测算,即确定单产和价格的边缘分布;二是确定两类风险的相关关系,即产量和价格的联合分布。常用的风险测算方法有参数法和非参数法两种。国外研究最早假设农作物单产服从正态分布[1],而Ramírez、Mcdonald发现农作物单产受诸多因素影响,是否服从正态分布要取决于当地的条件。此后,国外学者进一步提出农作物单产可能服从Beta分布、Lognormal分布和Weibull分布等[3-4]。由于价格具有非负性,所以大多学者认为农作物价格服从Log normal分布[5-6]。尽管学者们分别采用了不同的分布来提高风险测算的准确性,但事先对其分布进行假定,就可能导致估计结果不精确或费率估计结果不稳定等问题,本身就存在不合理之处。因此,非参数法逐步发展起来,Woodard[7]采用非参数核密度法对农作物单产、价格风险进行了测算,结果表明非参数核密度估计更加灵活,且能够体现出单产损失数据的非对称性和左偏性特点。文献[8]分别采用参数法和非参数法厘定了我国粮食单产纯费率,发现非参数核密度法厘定的费率结果更为准确,更加符合实际。在确定了单产、价格边缘分布的基础上,如何确定其联合分布至关重要,Copula理论的出现及发展使这一问题得到解决。Tejeda通过Copula方法发现农作物单产与价格之间存在微弱负相关性,并得出在风险“对冲效应”下,收入保险相较于产量保险具有更低费率的结论[3]。随后,有学者对Copula函数进行了改进,Woodard发现相较于单一Copula函数,混合Copula函数能够有效提高玉米收入保险费率厘定的准确性[9]。Goodwin等[10]采用vine-Copula对美国玉米和大豆收入保险进行了研究,结果表明vine-Copula具有更小的AIC和BIC值,相较于高斯Copula能更好的衡量尾部风险。国内当前只有少数学者通过Copula方法对农作物收入保险进行定价研究,且均采用参数法并依据AD统计量来选取最优分布对农作物单产、价格风险进行测算[11-13]。
综上,国外通过Copula方法研究农作物收入保险理论较为成熟,研究成果也较为丰富,而我国对这方面的研究才刚刚起步,尤其在非参数核密度估计与Copula函数在农作物收入保险综合应用研究方面。因此,本文在已有研究的基础上,通过非参数核密度估计与Copula函数相结合的方法来研究农作物收入保险费率厘定问题。具体来说,以山东省1975—2016年小麦单产、价格数据为基础,通过小波分析进行去趋势处理后,采用非参数核密度估计测算小麦单产、价格风险,依据平方欧式距离从常用Copula函数中选取最优Copula形式,采用极大似然估计得到Copula函数参数,结合蒙特卡罗方法随机抽样5 000次,最终得到不同保障水平下山东省小麦收入保险费率。
1 基本理论
1.1 非参数核密度估计
设X1,X2,…,Xn是取自一元连续总体的样本,在任意点x处总体密度函数f(x)的核密度估计[14]
(1)

(2)
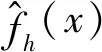
(3)
其中,A=min{样本四分位距/1.34,样本标准差}。
1.2 Copula函数
1998年,Nelsen给出了Copula函数的定义:
定义[16]Copula函数是指具有以下性质的函数C(u1,u2,…,uN):
1)C(u1,u2,…,uN)定义域为[0,1]N;
2)C(u1,u2,…,uN)有零基面,并且是N维递增的;
3)C(u1,u2,…,uN)有边缘分布函数Ci(ui)(i=1,2,…,N),且满足
Ci(ui)=C(1,…,1,ui,1,…,1)=ui
其中ui∈[0,1](i=1,2,…,N)。
下面的Sklar定理是Copula理论中的一个关键结果。
Sklar定理[16]Copula函数是随机变量x1,x2,…,xn的联合分布函数F(x1,x2,…,xn)与各自的边缘分布函数F1(x1),…,Fn(xn)相连接的一个函数,即存在函数C(u1,u2,…,un),满足
F(x1,x2,…,xn)=C[F1(x1),F2(x2),…,Fn(xn)]。
(4)
若F1(x1),…,Fn(xn)连续,则Copula函数C(u1,u2,…,un)唯一确定。F(x1,x2,…,xn)的密度函数为
(5)
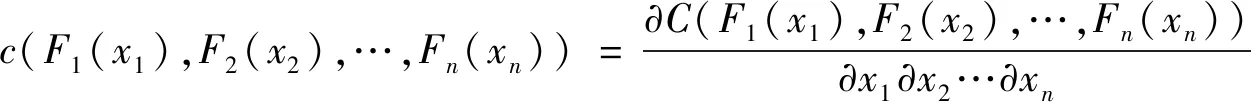
2 费率厘定方法
小麦收入保险定价主要涉及两个问题,一是对小麦单产、价格风险的估计,二是对二者相关性的测算。分别采用非参数核密度估计和Copula方法解决以上两个问题,在此基础上结合蒙特卡罗模拟方法计算出小麦收入保险费率,具体方法如下:
1)通过非参数核密度估计分别拟合小麦单产及价格风险分布,得到两个边际分布密度函数f1(x1),f2(x2),对应的分布函数为F1(x1),F2(x2);
2)通过Copula函数建立单产、价格风险分布的联合分布。采用极大似然估计法估计Copula参数,并依据平方欧式距离最小的原则从常用Copula函数中选取最优Copula形式;
3)以C(F1(x1),F2(x2))作为“随机数发生器”,生成服从[0,1]均匀分布的随机变量u,v各5 000个;
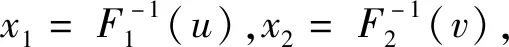
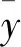

(6)
(7)
3 实证研究
3.1 数据处理

对每千克主产品平均出售价格数据进行相同处理,原始数据处理结果及去趋势处理后的小麦单产及价格序列描述性统计量分析见表1、表2。
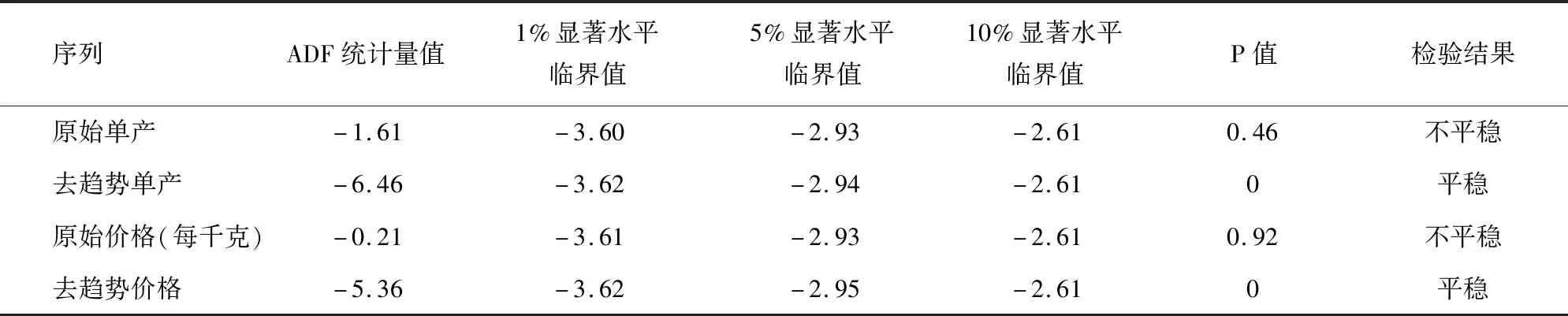
表1 原始序列及去趋势处理后序列单位根检验结果Tab.1 Unit root test results of original sequence and detrended sequence

表2 去趋势处理后小麦单产、价格描述性统计Tab.2 Descriptive statistics of wheat yield and price after detrending treatment
由表1、表2可知,去趋势处理后的单产、价格数据峰度系数均大于3,呈尖峰状态;偏度系数均大于0,呈右偏分布,且在1%显著性水平下均拒绝存在单位根的假设,即去趋势处理后的单产、价格序列为平稳序列。因此,可以通过非参数核密度估计对其分布进行拟合。
3.2 边缘分布确定
对小麦单产数据进行检验(KS检验、W检验)发现,小麦单产并不符合常见参数分布(正态分布、对数正态分布、伽马分布、指数分布),因此采用非参数核密度估计对小麦单产、价格数据边缘分步进行拟合。根据Silverman的“经验法则”计算单产、价格数据的窗宽分别为8.139和0.097,考虑到选取不同核函数可能对核密度估计结果产生影响,分别选取4种常用核函数对小麦单产、价格数据进行拟合,结果如图1、图2所示。可以看出,不同核函数之间差异不大,但高斯核函数更为平滑,更能反映小麦单产和价格的真实分布情况。
3.3 联合分布的确定
在得到小麦单产和价格的边际分布的基础上,可以通过Copula方法来计算两者的相关关系并模拟其联合分布。目前常用的二元Copula函数有5种,分别为正态Copula、t-Copula、Frank Copula、Gumbel Copula和Clayton Copula[14],采用极大似然估计法对Copula参数进行估计,结果如表3所示。

3.4 小麦收入保险费率的厘定
确定农户小麦收入的最优联合分布函数(t-Copula函数)后,由于Copula函数的具体解析式较为复杂,难以直接计算费率。因此,通过蒙特卡罗模拟方法模拟5 000对单产和价格数据,通过式(6)和(7)计算小麦收入保险纯费率。目前,山东省现行小麦保险费率在80%保障水平下为4%,为方便比较并考虑到农户选择保险的多样性,计算了75%~100%保障水平下的小麦收入保险费率,结果如图4和表4所示,图4中的左、下方柱状图分别表示蒙特卡罗模拟小麦价格及单产样本点的边际分布情况。
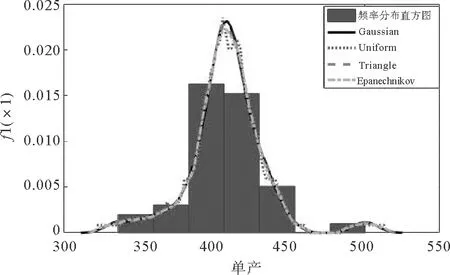
图1 小麦单产非参数核密度估计结果 Fig.1 Estimation results of nonparametric kernel density for wheat yield

图2 小麦价格非参数核密度估计结果Fig.2 Nonparametric kernel density estimation of wheat price

表3 Copula函数估计结果Tab.3 Copula function estimation results
需要指出的是,此处得到的费率为纯费率,不包括保险公司实际运营所需的附加营业费用等。从表4可以看出,保障水平的降低会使预期损失发生的概率下降,从而费率降低。在75%~100%保障水平下,山东省小麦收入保险纯费率在1.13%~6.71%之间,不同保障下费率存在较大的差异。
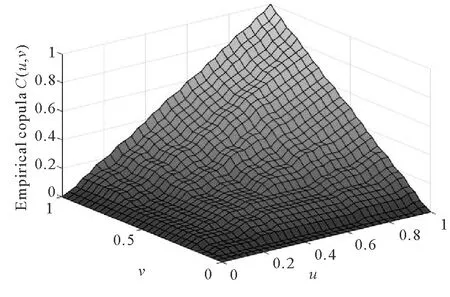
图3 小麦单产、价格经验Copula分布函数图Fig.3 Copula distribution function diagram of wheat yield and price experience

图4 蒙特卡罗模拟结果Fig.4 Monte Carlo simulation results
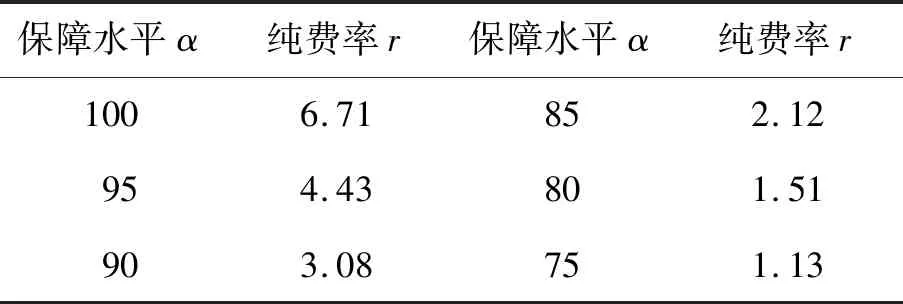
表4 山东省小麦收入保险费率厘定结果Tab.4 Determining results of wheat income insurance premium rate in Shandong Province %
4 结论
以山东省小麦历史单产、价格数据为基础,运用非参数核密度估计与Copula方法得到两变量的联合概率分布,最终得到不同保障水平下小麦收入保险费率,所得结论如下:
1)采用非参数核密度估计对小麦单产和价格风险进行测算,而不是事先假设其服从某种特定分布,避免了由于分布选择的主观性引起费率结果估计不稳定的问题,所测风险更加符合实际。
2)根据最小平方欧式距离选取t-Copula得到了山东省小麦单产和价格的联合概率分布,kendall-τ相关系数为-0.086 2,说明山东省小麦单产和价格数据并不是完全独立的,而是呈现出微弱的负相关性。
3)目前山东省实施的小麦产量保险在80%保障水平下费率为4%,高于通过本文方法测算的收入保险费率1.51%,原因是小麦单产与价格风险之间存在对冲效应,因此收入保险费率一般会低于同保障水平的产量保险费率,并且计算结果为纯费率,并未考虑保险公司的附加营业费用和巨灾风险等因素,这也是所得费率偏低的原因之一。另外,测算的不同保障水平下小麦收入保险纯费率差异明显,保险者应当根据自身情况选择适当的保障水平购买保险。
