抑制油气井钻柱黏滑振动控制器设计与应用

付 蒙，吴亚锋，宋叔飚，李江红，张文龙

(西北工业大学 动力与能源学院，西安 710072)

应用于油气井钻进的钻柱系统主要包括位于地上的顶驱、由许多节钻杆连接而成的钻柱以及井底钻具组合(Bottom Hole Assembly,BHA)。近年来，钻柱系统的驱动主要由顶驱取代转盘而完成。顶驱主要包括驱动电机、减速器等。顶驱提供了恒定的钻柱系统扭矩(或者驱动转速)；钻柱用于向井底钻具传递驱动扭矩，同时为钻井液循环提供流通通道；井底钻具组合用于提供转动惯量；位于井底钻具组合的钻头用于钻探[1-2]。由于钻柱(钻杆)横截面积很小、钻柱长度可达几千米导致钻柱扭转刚度低，井底钻具组合转动惯量小，钻头和岩石间存在非线性摩擦力和剪切应力。钻柱系统受到非线性扰动(Torque on Bit,TOB)的作用，容易引发钻柱黏滑振动现象[3]。

钻柱黏滑振动主要表现为，驱动扭矩振荡，顶驱驱动转速小幅度波动，钻头转速“黏滞-滑动-黏滞”周期性交替出现[4]。钻柱黏滑振动属于一种剧烈的低频振动，钻头转速振动幅值可以达到正常转速的3～9倍[5]。钻柱黏滑振动会使钻进速度降低，导致钻柱和钻头使用寿命减短，进而严重影响钻进效率，威胁钻井安全[6]。钻柱黏滑振动属于由非线性摩擦力引发的自激振动[7]。

为抑制钻柱黏滑振动，消除振动对钻进的影响，相关文献提出一些控制方案。Jansen等设计一种主动阻尼控制系统，降低钻柱系统的临界转速，扩大系统无振动旋转的工作范围。Pavkovic等在主动阻尼系统基础上提出基于钻柱扭矩估计的比例积分控制器。Serrarens等提出H∞控制器，提高钻柱系统的鲁棒性。Tucker等[8]基于钻柱分布式空间模型，设计比例积分控制器。但是，以上方案中只有一个状态反馈回路，导致其控制效果受到限制。Abdulgalil等[9]与Al-Hiddabi等[10]分别提出一种多维非线性状态反馈控制器，Navarro-López等[11]与Liu[12]分别提出滑模控制器来抑制钻柱的黏滑振动，Puebla等[13]提出基于模型误差补偿的控制方法。这些方案仍然需要获取所有的状态反馈量，但是钻柱系统只有顶驱驱动转速与驱动扭矩可测。并且这些方案只适用于理论研究，没有考虑到电机动力学，没有进行井上实验。

针对上述不足，本文提出了一种速度补偿反馈控制器抑制钻柱黏滑振动，提高系统抗干扰能力，基于此设计了钻柱黏滑振动控制系统，并应用于钻井现场实验。该研究的主要创新在于，一方面只需要获取可测的顶驱驱动转速和驱动扭矩，即可完成多维状态反馈速度控制器的设计；另一方面提出的控制方案通过PLC(Programmable Logic Controller)、变频器和电机等执行器得以实现，并将设计的控制系统应用于钻井现场。文章建立了钻柱系统非线性动力学模型；设计了估计井底状态的观测器和抑制钻柱黏滑振动的速度补偿反馈控制器；为测试控制效果，首先在MATLAB中完成了对闭环控制系统的仿真验证；将设计的钻柱黏滑振动控制系统应用于钻井现场。

1 钻柱系统非线性动力学模型

为实现钻柱系统仿真，验证所设计控制器的性能，建立了钻柱系统非线性动力学模型，如图1所示。该动力学模型包括双自由度集中质量模型和非线性扰动扭矩模型。Serrarens等指出，图1所示的钻柱系统模型可以满足钻柱系统振动机理研究和抑制黏滑振动控制算法研究的需求。

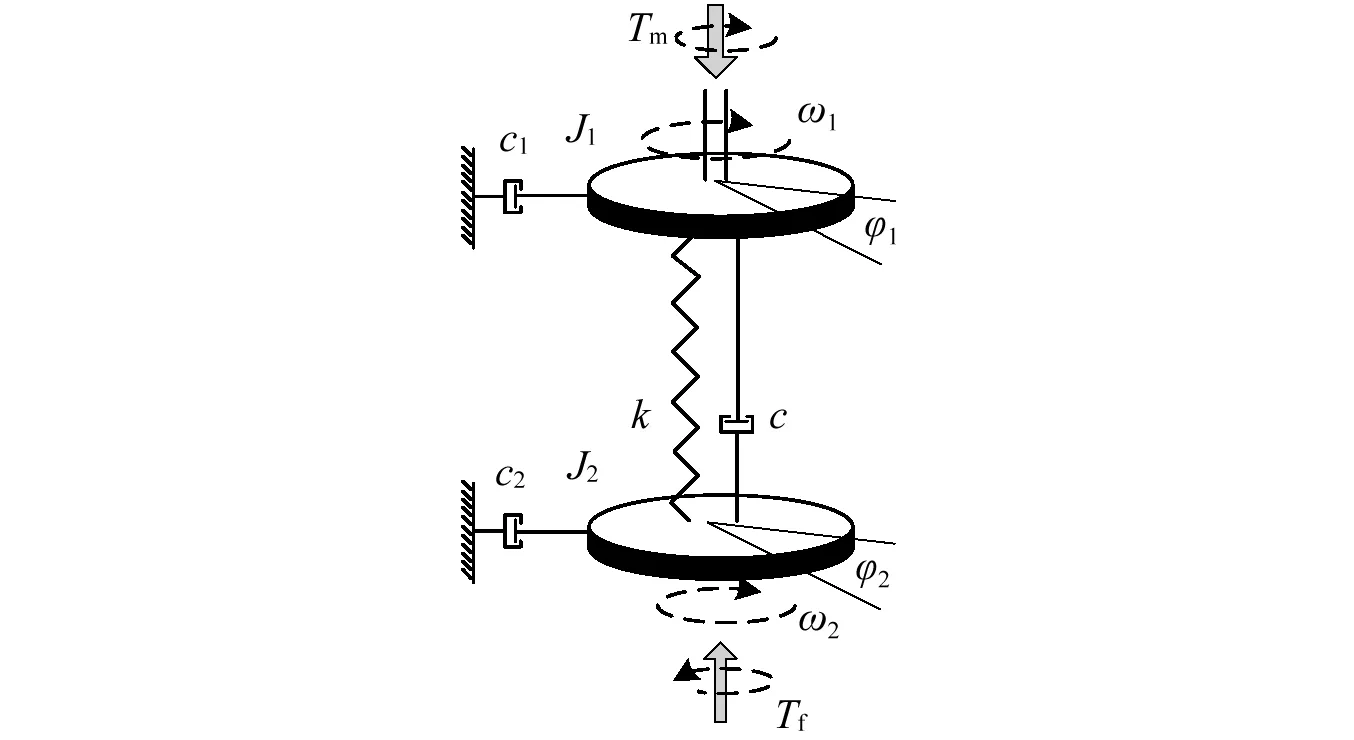
图1 钻柱系统双自由度集中质量模型Fig.1 Lumped parameter model of drill string system

基于Jansen等对钻柱系统的假设，忽略电机动力学，钻柱双自由度集中质量模型可以表示为

(1a)

(1b)

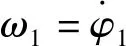
式(1a)和式(1b)的模型参数中，J1可直接由顶驱变频器辨识，J2可通过对BHA转动惯量测量获取，c1可通过对顶驱能量实验获取，c2一般难以获取并且数值并不唯一(井底钻具组合阻尼系数一般比较小，范围大概为0～50 N·m·s/rad)，钻柱阻尼系数c

(2)

式中：cl为钻柱单位长度阻尼系数;L为钻柱长度。

式(1)中，钻柱刚度系数k为

(3)

式中:G为钻柱剪切模量；do为钻柱(钻杆)外径；di为钻柱(钻杆)内径。

式(1b)中的非线性扰动扭矩Tf为钻头转速的函数。为较准确地描述钻具和岩石间的相互作用过程，特别地为较准确地描述钻具转速在黏滞区间的连续性，利用Karnopp摩擦模型模拟钻具受到的扰动扭矩Tf[14]。该非线性扰动扭矩的表达式

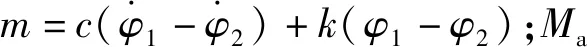
2 控制方案设计

根据钻柱黏滑振动的表现特征和钻柱系统的工作环境，文章有针对性地设计了速度补偿反馈控制器，进而抑制钻柱黏滑振动。设计的速度补偿反馈控制器为一种线性控制器。Pavkovic等指出，线性电机速度控制器可以抑制非线性钻柱黏滑振动的发生。设计的控制方案如图2所示。

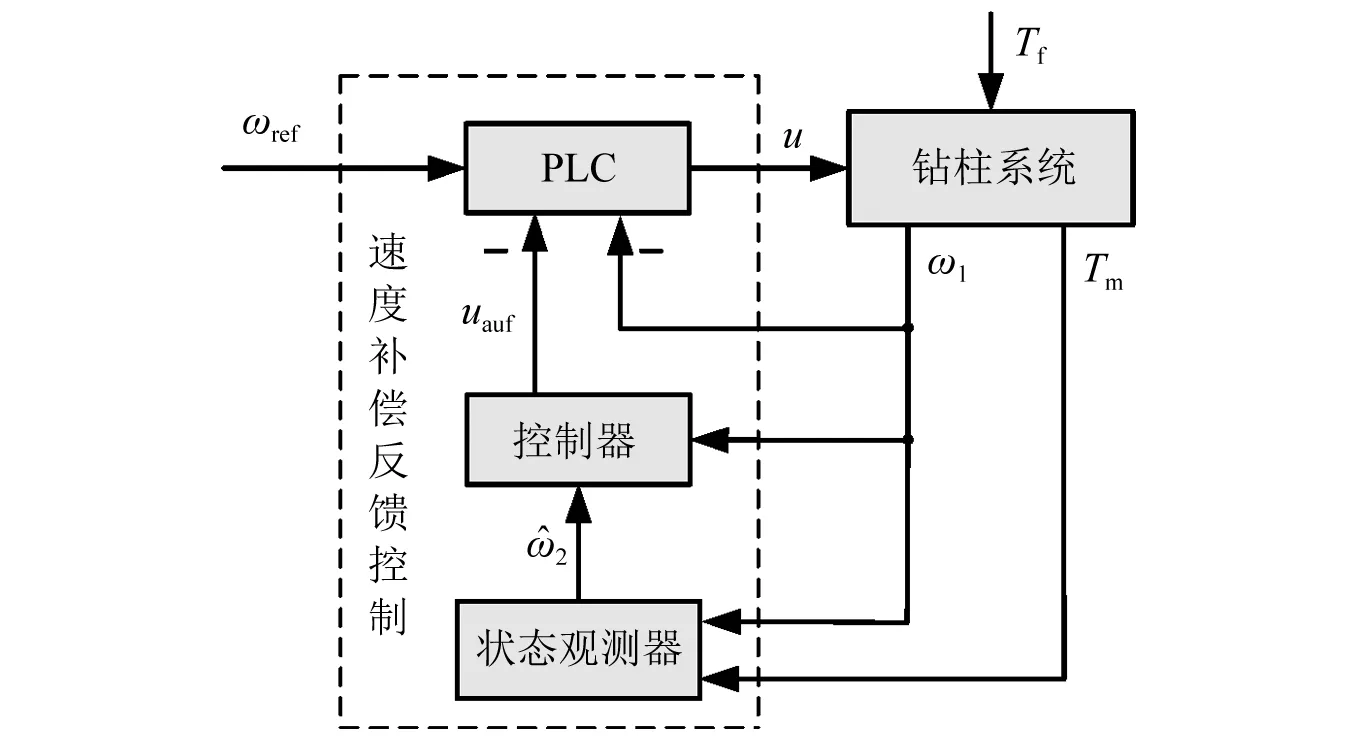
图2 控制方案结构图Fig.2 Lumped parameter model of drill string system

钻柱系统深入地下几千米，只有顶驱驱动转速与驱动扭矩可测，其他系统状态量位于地下难以直接测量。为实现多维状态反馈控制器，设计了状态观测器估计井底钻头转速ω2。控制器设计过程中，假定顶驱阻尼系数c1、井底钻具组合阻尼系数c2及钻柱阻尼系数c为零。这样会增加控制难度，同时也会增加闭环控制系统的鲁棒性。速度补偿反馈控制器设计主要包括：①状态观测器设计；②辅给定转速控制器设计；③速度补偿反馈控制器。

2.1 状态观测器

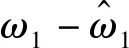
(5)

(6)

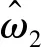
状态观测器(式(5)与式(6))设计的最大优点在于，只需要顶驱转动惯量J1和钻柱刚度系数k，不需要获取其他系统参数，即可完成观测器的设计。在实际钻进中，顶驱转动惯量J1和钻柱刚度系数k抗外部干扰能力强，不容易被改变，这样就降低了钻柱系统建模误差对状态观测器设计的影响。

2.2 辅给定转速控制器

根据钻柱黏滑振动的表现特征，控制目标可以表示为ω2→ω1。基于状态观测器，设计控制器计算辅给定转速指令补偿驱动转速。辅给定转速指令可以表示为

(7)

式中:kP2和kI2为控制器增益。

2.3 速度补偿反馈控制器

假定顶驱内变速箱的减速比为n，则顶驱驱动转速转换到电机侧为nω1，辅给定转速转换到电机侧为nuauf，控制目标表示为(nω1+nuauf)→ωref。结合PI(Proportional Integral)控制器(嵌入于PLC中)，设计速度补偿反馈控制器

(8)

式中：kP1和kI1为控制器增益;u为控制器输出。如果考虑实际钻柱系统的执行器，u为电机的驱动扭矩，则钻柱侧驱动扭矩Tm=nu。

由式(7)与式(8)可知，设计的速度补偿反馈控制器属于状态反馈控制器，并不包含钻柱参数。这样有效地避免了由建模误差对控制效果的影响。

观测器增益和控制器增益由最优阻尼原理计算。最优阻尼原理指出，当闭环系统特征比为0.5时，系统阶跃响应超调大约为6%，调整时间大约为1.8倍的控制时间常数[15]。最优阻尼原理是一种基于闭环特征多项式的解析设计方法，一方面可以保证系统有比较好的动态特性；另一方面可以使观测器的阻尼最佳。

3 仿真分析

基于非线性动力学模型(式(1a)、式(1b)和式(4))，在MATLAB中完成了对钻柱系统的仿真。以该模型为被控对象，分析了状态观测器(式(5)与式(6))的估计效果和速度补偿反馈控制器(式(8))抑制钻柱黏滑振动的控制效果及其动态性能。在仿真环境下，忽略电机动力学，忽略减速比(n=1)。控制器的输出为驱动扭矩，并直接作为钻柱系统的输入。为仿真钻柱黏滑振动现象，钻柱双自由度集中质量模型参数主要来源于文献[1]、文献[4]、文献[9]。其中，钻柱长度L=2 000 m，钻柱剪切模量G=7.96×1010N/m2，钻柱单位长度阻尼系数cl=0.034 8 N·m·s/rad。非线性扰动扭矩模型主要来源于文献[5]、文献[11]。具体参数如表1所示。

表1 钻柱模型力学参数Tab.1 Parameters of drilling system

根据最优阻尼原理，计算状态观测器的增益Ko=[13.33,188 622,628 740]。选择速度补偿反馈控制器增益[kP1=100,kI1=50,kP2=0.2,kI2=0.1]。仿真中，系统输入参考值为ωref=15 r/min。

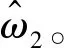
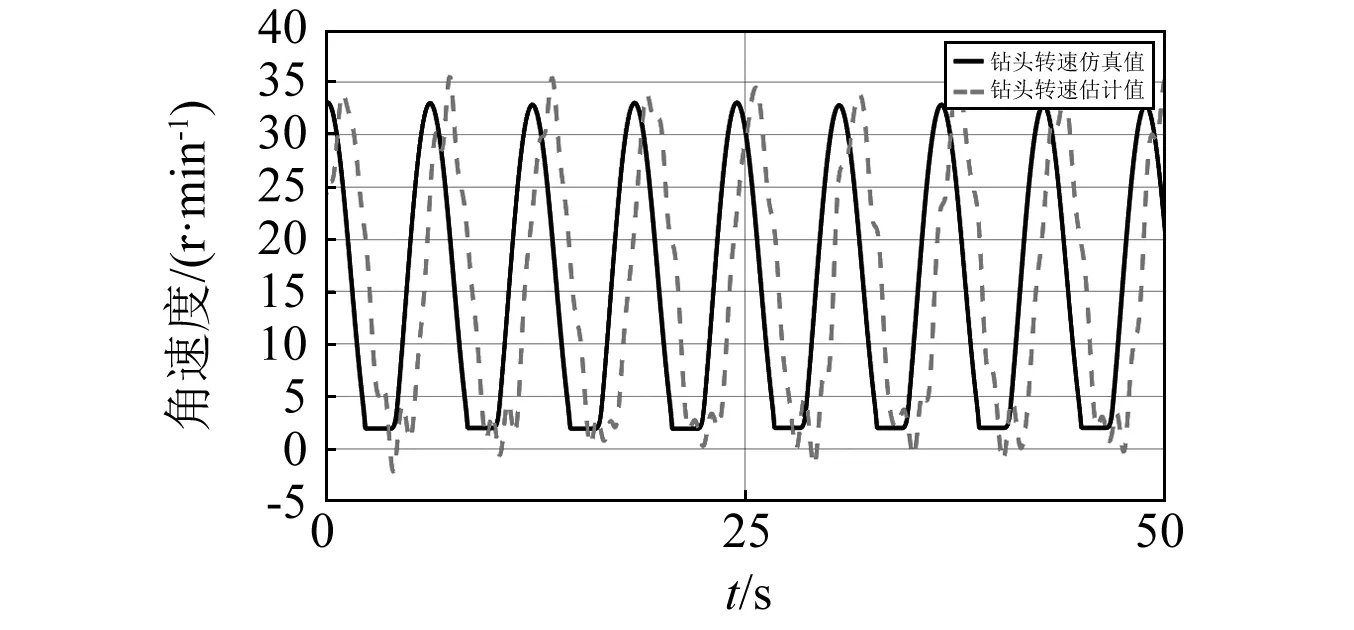
图3 钻头转速ω2和钻头转速估计值时间响应曲线Fig.3 True drill bit speed ω2 and estimated speed

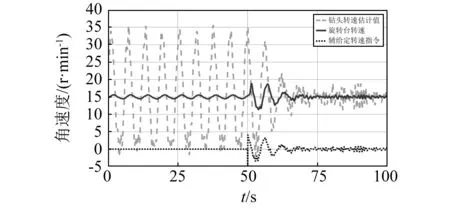
图4 钻头转速估计值顶驱驱动转速ω1和辅给定转速指令uauf时间响应曲线Fig.4 Estimated drill bit speed rotary table speed ω1 and auxiliary speed uauf

如图5所示，在发生黏滑振动时(小于50 s)，驱动扭矩表现出比较剧烈的波动。控制器启动之后，驱动扭矩波动幅值被有效地抑制。综上所述，设计的速度补偿反馈控制器可以有效地抑制钻柱黏滑振动，可以试用于钻井现场。

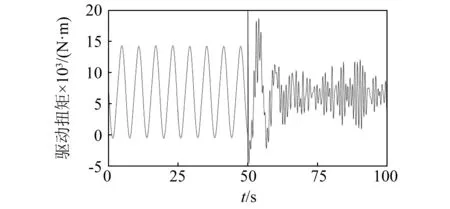
图5 驱动扭矩Tm时间响应曲线Fig.5 Drive torque Tm

4 井场实验

为了验证设计的速度补偿反馈控制器(式(8))对钻柱黏滑振动的控制性能、自抗扰性和实用性，进行了井场实验。基于速度补偿反馈控制器设计了钻柱黏滑振动控制系统，如图6所示。图6中所包含的控制算法为式(7)。PI控制算法以程序方式嵌入于变频器的PLC中。该系统还包括硬件设计、软件设计、控制算法的实现、信号处理的方法、与变频器的通讯等诸多方面。在此并不做详细赘述。图7为钻井现场。

图6 钻柱黏滑振动控制系统Fig.6 The control system

图7 钻井现场Fig.7 Drilling field

实际系统中，系统输入参考值ωref由操作员在变频器面板设定(或者在司钻台设定)。变频器内PLC的输入还包括辅给定指令(速度补偿指令)uauf和顶驱驱动转速反馈值ω1。变频器的输出与顶驱内电机连接。为防止异常操作，对顶驱的输出扭矩做限幅处理。

系统输入参考值约为960 r/min。顶驱变速箱的减速比10.3，所以输入参考值转换到钻柱一侧大概ωref=94 r/min。钻井压力大概WOB=100 000 N。实时钻井深度为3 500 m。所使用钻杆的内径为85 mm，外径为107 mm。按照式(3)可知，钻柱的刚度系数约为k=176 N·m·rad。顶驱转动惯量转换到钻柱一侧J1=1 473 kg·m2。尽管钻柱系统会受到井下环境中不确定性因素的影响，但是设计的控制器并不依赖于其他钻柱系统参数。闭环控制系统可以提高抗不确定性因素的能力。

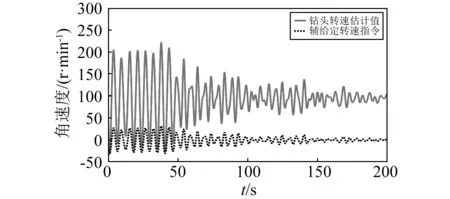
图8 钻井现场钻头转速估计值顶驱驱动转速ω1和辅给定转速指令uaufFig.8 Estimated drill bit speed rotary table speed ω1 and auxiliary speed uauf in drilling field

因此，设计的观测器可以用于诊断钻进过程中钻柱黏滑振动是否发生。图9为顶驱驱动扭矩Tm。由图9可知，发生钻柱黏滑振动时驱动扭矩Tm会剧烈波动。

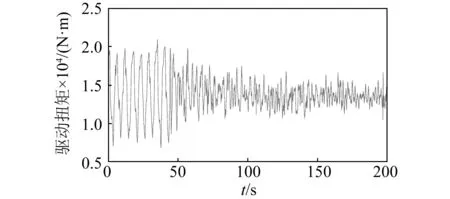
图9 钻井现场驱动扭矩TmFig.9 Drive torque Tm in drilling field

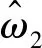
钻井现场，还可以通过Starter软件来实时监测电机实际转速和驱动扭矩，并检测控制器的控制效果和控制性能。Starter软件是与变频器相配套的现场检测工具。电机驱动扭矩发生剧烈波动时，启动钻柱黏滑振动控制系统，其Starter软件检测到的控制效果，如图10所示(Starter软件只能显示电机侧的实时数据)。其中，实时钻井深度为2 800 m，则钻柱的刚度系数约为k=220 N·m·rad。

图10中，灰线代表电机的实际转速为nω1，白线代表电机的驱动扭矩为Tm/n，黑线代表辅给定转速为uauf，横坐标单位为ms。由图10可知，启动钻柱黏滑振动控制系统后(约106 s处)，电机的驱动扭矩Tm/n振动程度被得到有效抑制。值得注意的是，图8中的辅给定转速指令uauf为辅给定转速控制器的输出指令，而图10中检测到的辅给定转速uauf为PI控制器的输入指令。因此，在启用控制系统之前，图8中有辅给定转速输出，图10中辅给定转速为零。

图10 钻井现场由Starter检测到的顶驱驱动转速nω1、驱动扭矩T/n和辅给定转速指令uaufFig.10 Rotary table speed ω1,drive torque Tm and auxiliary speed uauf obtained by Starter in drilling field

综合上述实验结果可知，基于速度补偿反馈控制器设计的钻柱黏滑振动控制系统可以应用于抑制钻井过程中发生的钻柱黏滑振动。

5 结 论

建立了钻柱系统非线性动力学模型，提出了速度补偿控制方案提高闭环系统抗干扰能力，设计了钻柱黏滑振动控制系统。在仿真环境下，测试控制器的性能。然后将设计的控制系统直接应用于钻井现场。得到的主要结论如下：

(1)仿真结果表明，非线性动力学模型可以应用于模拟钻柱系统，设计的状态观测器可以诊断井底钻具组合是否发生钻柱黏滑振动。

(2)仿真中，启用速度补偿控制器后，波动的钻头转速估计值与驱动扭矩逐渐收敛，表明钻柱黏滑振动被有效抑制，且闭环控制系统调节时间短、超调小、动态性能好。

(3)现场实验表明，钻柱黏滑振动控制系统可以有效抑制钻井过程中发生的钻柱黏滑振动；控制效果符合钻进要求，设计的钻柱黏滑振动控制系统可以应用于钻井现场。