高速角接触球轴承保持架不稳定运动机理分析

张 涛，陈晓阳，顾家铭，赵利锋

(1.上海大学 机电工程与自动化学院，上海 200072；2.上海天安轴承有限公司，上海 201108；3.上海集优机械股份有限公司轴承研发中心，上海 201108)

作为关键支承部件的角接触球轴承，在精密机床、新能源汽车、航空航天等领域有着十分广泛的应用。随着主机工作性能要求的提高，对轴承的转速、旋转精度和可靠性提出了更高的要求。保持架的不稳定运动，一方面会使轴承摩擦力矩波动，产生振动和啸叫声；另一方面，会导致保持架与球及套圈挡边的碰撞力增大，从而加剧接触副的摩擦磨损，当磨损量达到一定值时，会使轴承不能满足主机工作精度要求而提前失效[1]。保持架的过量磨损和严重失稳甚至会导致保持架突然断裂，致使轴承卡死而引起灾难性的后果。自20世纪70年代以来，高速滚动轴承的动态性能特别是保持架的不稳定性问题就引起了人们的重视，并且一直是研究的热点、难点。Walters[2]最早建立了球4自由度，保持架6自由度的球轴承动力学模型，模型中考虑了润滑的影响但对球的运动进行了约束。Kannel等[3]建立了保持架平面运动的角接触球轴承动力学模型，详细分析了球与保持架的摩擦、润滑剂黏度及球与滚道弹流润滑拖动性对保持架运动稳定性的影响。Gupta[4]详细分析了球与滚道，保持架与球及套圈挡边的相互作用，建立了滚动轴承完全动力学模型，可以模拟时变工况下轴承零件的瞬态运动特性。Meeks等[5]对动力学模型进行了简化，球的运动和载荷分布由拟静力学结果确定，只需求解保持架的运动微分方程，从而提高了计算效率，并以球与保持架兜孔的摩擦功耗和碰撞力峰值为准则，对保持架兜孔和挡边间隙进行了优化分析。与此同时，Gupta等[6]通过对球的平衡约束消除球与滚道的高频弹性振动，从而增大积分步长，提高计算效率，并能够有效地研究保持架的低频特性。在此模型基础上，Gupta[7-9]系统研究了工况、几何、摩擦等因素对保持架稳定性的影响，对滚动轴承的性能优化具有重要参考价值。在过去的几十年里，滚动轴承动力学模型不断发展完善，越来越贴近实际工况，对保持架几何缺陷、结构不对称、柔性体化的仿真都已成为可能[10-13]。国内对滚动轴承动力学的研究近些年才有较快发展，主要采用两种方法研究保持架的动态特性：一种是以Gupta模型为基础，开发的滚动轴承动力学分析程序[14-15]；另一种是以通用多体动力学和有限元软件为平台进行仿真分析[16-18]。Liu等和Ye等课题组分别开发了高速滚动轴承动力学分析程序，但主要针对充分供油的航空发动机主轴轴承，结合具体算例探讨了工况和几何参数对保持架稳定性的影响。保持架不稳定运动的试验研究相对较少。Kingsbury[19]首先分析了配对角接触仪表球轴承摩擦力矩的扰动和保持架的运动，指出保持架的涡动是球与保持架摩擦耦合的结果，导致了摩擦力矩的低频扰动；Kingsbury等[20]后来对仪表球轴承稳定运转时和发生啸叫时保持架的运动进行了试验研究，发生啸叫时，发现保持架在随球组旋转运动的基础上有高频的涡动，涡动频率与球的自旋速率有关。

综上所述，文献中所讨论的工况、几何、摩擦等因素对保持架稳定性的影响都是间接的，而保持架的运动是由保持架与球及套圈挡边的相互作用决定的。套圈挡边平衡球对保持架的作用力及保持架的离心力，起到约束保持架不稳定运动的作用。据此推断，保持架的不稳定运动主要与球的作用有关。本文以惯性仪表中支承高速转子的角接触球轴承为研究对象，建立球轴承动力学磨损数值仿真模型，分析不同工况下保持架的运动，试图从球与保持架兜孔碰撞点的位置、碰撞力的大小和频率以及碰撞点切向力的方向阐释保持架不稳定运动的机理。

1 模型建立及程序校验

1.1 高速仪表转子轴承动力学模型的建立

根据Gupta研究中的滚动轴承动力学建模方法，建立了高速仪表转子轴承动力学磨损数值仿真模型。模型中假定轴承组件的质心与几何中心重合；球和保持架具有6个自由度，外圈质心固定，内圈质心具有3个自由度；润滑的影响通过设定合理的摩擦系数来考虑，对于含油保持架自给润滑的仪表球轴承，不考虑球与保持架及保持架与套圈挡边之间的流体动压作用；所有接触按Hertz弹性接触和Coulomb摩擦计算法向力和切向力。利用变步长四阶Runge-Kutta法求解轴承的运动微分方程。模型简要介绍如下，详细的建模过程参考文献[21-22]。

1.1.1 坐标系定义及运动学方程

轴承零件的质心运动在惯性坐标系中描述，绕质心的转动在定体或方位坐标系中描述。坐标系定义见图1。惯性坐标系原点Oi位于外圈沟曲率中心轨迹圆的圆心，Xi沿轴承轴向，Zi垂直向上。方位坐标系原点Oa固定于球心，Xa沿轴承轴向，Za轴径向外指，其中dm为轴承节圆直径，ψ为球的方位角。保持架坐标系原点Oc固定于保持架几何中心，Xc沿保持架轴向，Zc指向第一个兜孔中心。

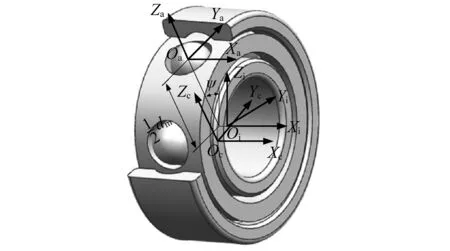
图1 坐标系定义Fig.1 Coordinate system

从惯性坐标系到定体坐标系的转换可通过三次相继的旋转实现，转换矩阵为

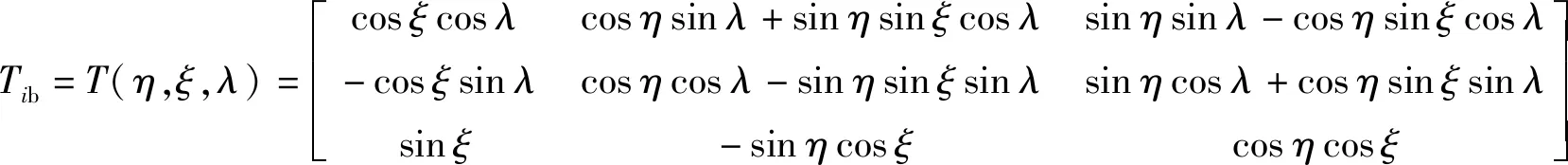
(1)

Gupta推导了轴承零件角速度与旋转角 (η,ξ,λ)之间的关系，得到如下运动学方程

(2)

式中:(ω1,ω2,ω3)为轴承零件角速度分量。

1.1.2 平衡约束及运动微分方程

图2 载荷作用前后角位置ψj处球中心和沟道曲率中心的位置Fig.2 Positions of ball center and raceway groove curvature centers at angular position ψj with and without applied load

为消除球与滚道之间弹性接触引起的高频振动，并能有效地研究保持架的低频特性，模型中对球的运动采用了平衡约束。即在每一时间步，球心的轴、径向运动微分方程由球与滚道的法向力平衡方程代替。球心的位置在惯性圆柱坐标系中描述，其轴、径向位置由平衡方程确定。角位置ψj处球受到的作用力如图3所示，球的平衡约束方程为

Qijsinαij-Qojsinαoj=0

Qijcosαij-Qojcosαoj+Fcj=0

(3)

式中：Qij,Qoj为球与内、外圈的法向接触力，其中下标i,o指内、外圈。Fcj为球的离心力。图3中，Fitxj,Fityj为内圈作用于球上的切向力，Mgj为陀螺力矩，Qcj为保持架与球的碰撞力。

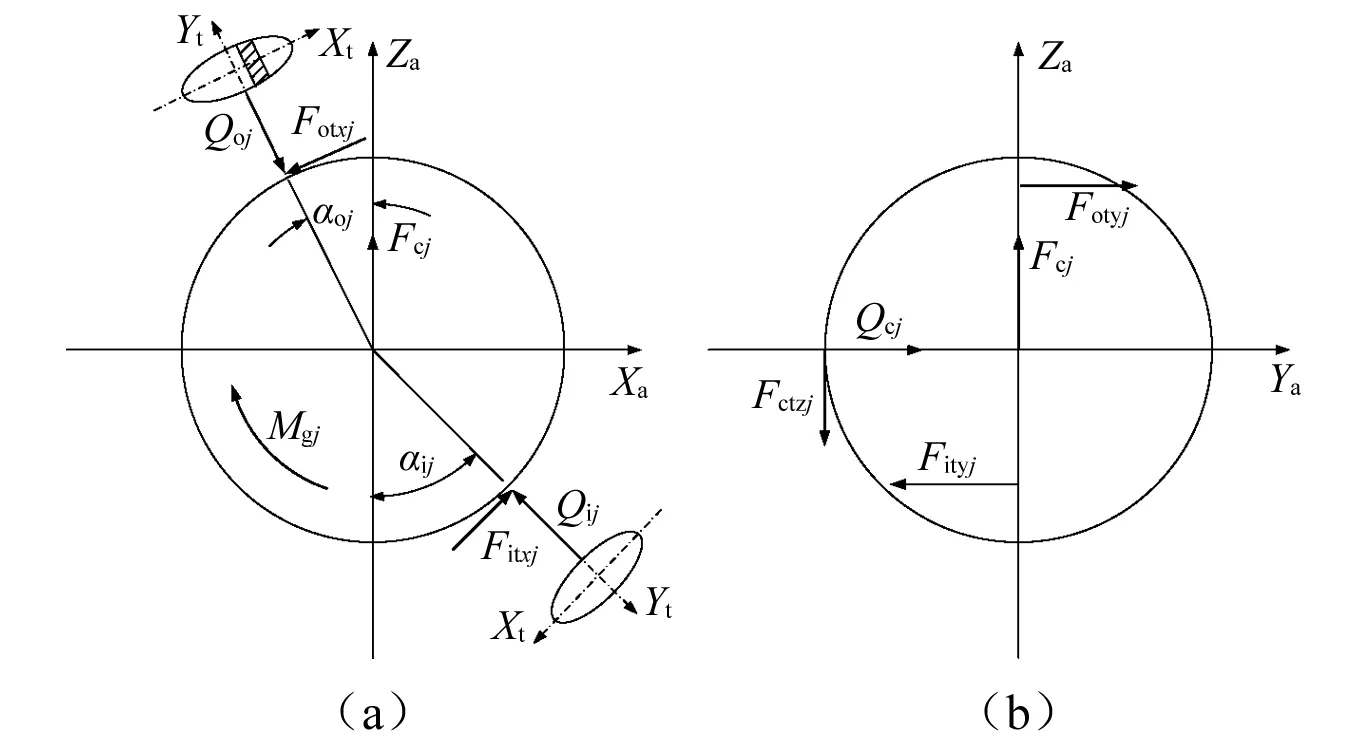
图3 角位置ψj处球上的作用载荷Fig.3 Ball loading at angular position ψj

内圈质心的位置同样由平衡方程确定，内圈质心具有3个自由度，其平衡方程为

(4)

式中：Fx,Fy,Fz为作用于内圈的轴向、径向外载荷；N为球数。

由于球与滚道的切向力相对法力较小，为提高计算效率，平衡方程中未考虑切向力。

球心的轴、径向位置及内圈质心位置由以上平衡方程联立求解确定，球心在圆周方向的位置由微分方程式(5)确定。球的质心运动和动量矩方程为

(5)

(6)

保持架的质心运动和动量矩方程为

(7)

(8)

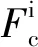
由质心运动方程和动量矩方程，与Gupta运动学方程联立求解，即可描述轴承零件的一般运动规律。

1.1.3 轴承零件时间平均磨损率的计算

对于高速角接触球轴承，球与滚道之间存在差动滑动、自旋滑动和陀螺滑动，且保持架与球及套圈挡边之间也存在较大滑动，接触区摩擦发热和磨损不可避免。根据Archard黏着磨损理论公式[23]

(9)

式中：w为零件的磨损率；K为Archard磨损系数；H为材料的布氏硬度；Q，V分别为载荷和滑动速度。对球与滚道的接触，接触椭圆短轴一般较窄，滑动速度沿短轴的变化可以忽略。因此将椭圆接触区沿长轴等距条形划分，如图4所示。分别计算各窄条上等效载荷和滑动速度的乘积QkVk，然后求和得到整个接触区内QV值，代入上述公式计算磨损率。对于球/保持架及保持架/引导套圈的相互作用，由于滑动速度较大且接触区较小，可以作为点或线接触来计算瞬时磨损率。得到了任意时刻的瞬时磨损率，即可计算时间T内的平均磨损率

(10)

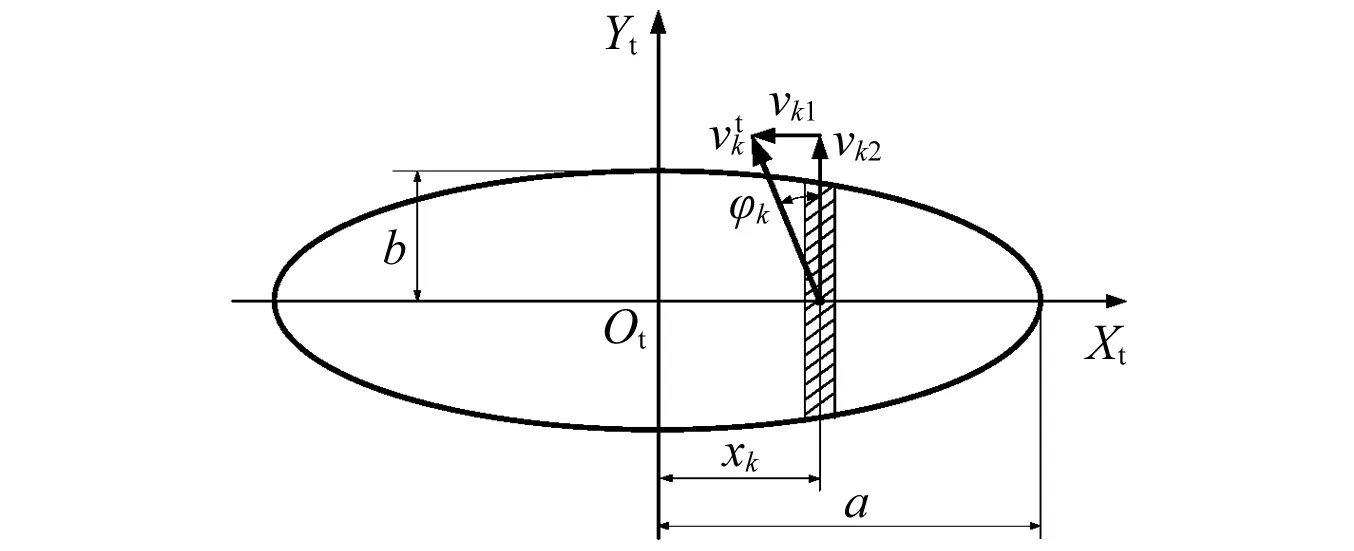
图4 接触椭圆内窄条中心处的滑动速度Fig.4 Sliding velocity in the contact ellipse

时间平均磨损率综合反映了零件间相互作用力的大小和频率，可以作为保持架稳定性定量判断的依据。

1.2 动力学程序框图及校验

根据上述动力学模型，编写了角接触球轴承动力学磨损数值仿真分析程序。图5所示为程序流程图。

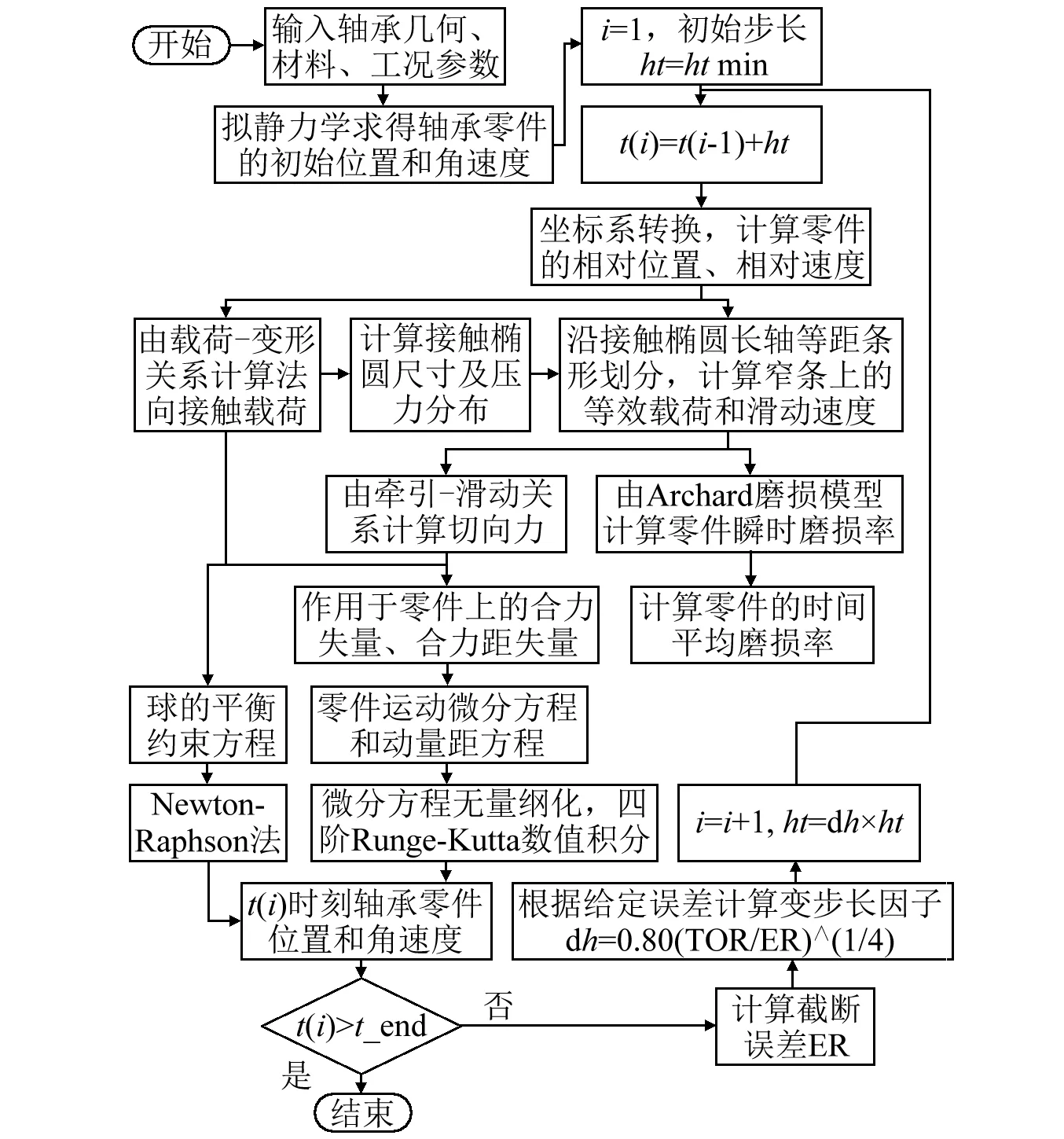
图5 角接触球轴承动力学磨损数值仿真程序框图Fig.5 Flow chart of the dynamic wear simulation program of angular contact ball bearings

与Gupta研究中2号角接触球轴承算例对比校验球和保持架的时间平均磨损率，与3号角接触球轴承算例的仿真和试验结果对比校验保持架的质心运动。图6所示为保持架和球(No.1指初始时刻方位角ψ=0)的时间平均磨损率可以看出，本文结果与Gupta滚动轴承动力学分析程序ADORE的仿真结果变化趋势一致，数量级一致，数值上也较为接近。图7所示为保持架质心运动轨迹，本文结果与Adore仿真结果及Gupta试验结果相吻合，保持架质心涡动半径约等于保持架/套圈的径向半径间隙。以上对比验证了本文程序的正确性、可靠性。

图6 球与保持架的时间平均磨损率Fig.6 Time-averaged wear rates of ball and cage

图7 保持架质心运动轨迹Fig.7 Orbits of cage mass center

2 结果与分析

利用已校验的程序，以某仪表转子轴承为算例，分析了不同载荷工况和保持架间隙比下保持架的运动。深入研究了球与保持架兜孔碰撞点角位置、碰撞力的大小和频率以及碰撞点切向力的方向对保持架不稳定运动的影响。保持架间隙比定义为球/保持架兜孔间隙(B)与保持架/套圈挡边间隙(R)之比，如图8所示。球与保持架兜孔碰撞点角位置的定义见图9。轴承结构和材料参数列于表1。根据Archard磨损公式，时间平均磨损率与磨损系数成正比，目前程序引用文献[23]中的磨损系数计算得到磨损率的变化趋势。根据文献[24-25]中拖动系数与油膜参数的关系，对含油保持架自给润滑轴承计算得球与滚道的拖动系数为0.11，保持架与球及引导挡边的摩擦系数设为0.05。

2.1 不同载荷工况的结果

某仪表转子轴承的工况为，轴向预紧载荷7 N，内圈转速30 000 r/min。为便于对比分析，假定由于转子重力产生的径向载荷为5 N，转子质心偏移产生的旋转径向负荷也为5 N。分析得到了纯轴向载荷、轴向径向联合载荷以及轴向旋转径向联合负荷下保持架的质心运动轨迹，球与保持架的角速度，球与兜孔碰撞点角位置、碰撞力及保持架兜孔的磨损率，结果如图10所示。

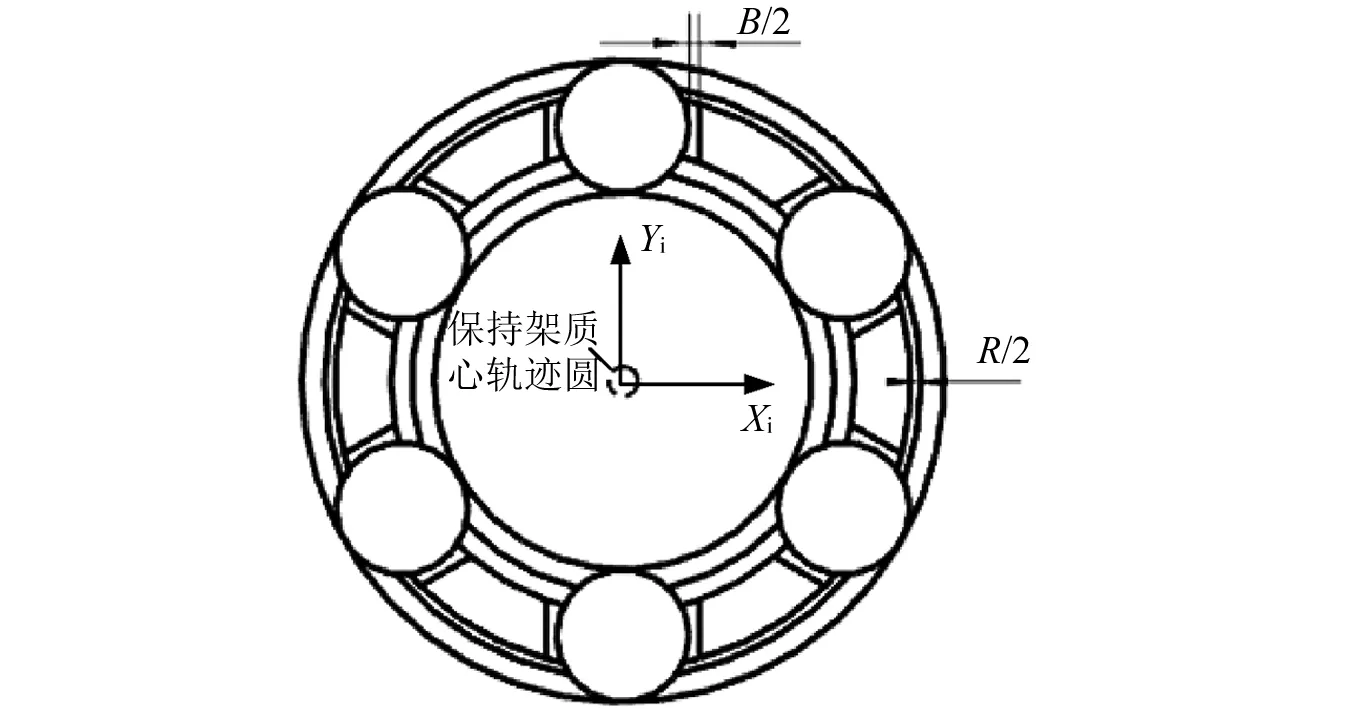
图8 保持架间隙Fig.8 Cage clearance

图9 球与保持架兜孔碰撞点角位置Fig.9 Angle position of ball and cage pocket collision

表1 轴承几何和材料参数Tab.1 Bearing geometry and material properties

表1 轴承几何和材料参数(续)Tab.1 Bearing geometry and material properties

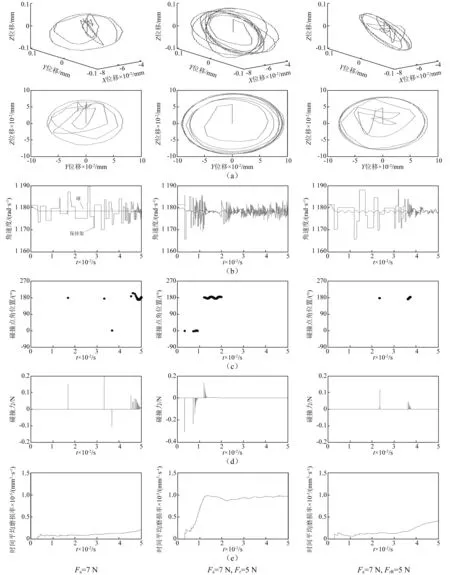
图10 不同载荷工况下的结果比较Fig.10 Results under different load conditions

图10(a)所示为保持架质心三维和二维轨迹图。可以看出在轴向载荷下，保持架质心运动不在径向平面内，轴向方向上有摆动，并趋于绕轴承中心稳定涡动，涡动半径约等于保持架兜孔直径间隙的一半。在轴向径向联合载荷下，保持架质心轴向摆动明显，质心涡动半径较大，说明保持架运动不稳定。轴向和旋转径向负荷下，保持架质心运动有偏斜，达到稳定涡动时的轨道半径比兜孔半径间隙稍大，是因为在径向载荷下，球组中心偏离轴承中心，保持架中心随之偏移，在离心力的作用下产生稳定的涡动，球组的径向位移加上保持架的离心力使保持架的涡动半径增大。

图10(b)所示为1#球轨道角速度和保持架自转角速度。由于保持架随球组转动，其角速度约等于球的轨道角速度，轴承运转过程中球与保持架的无规律碰撞导致保持架的角速度频繁波动。在轴向载荷下，球的公转速度恒定，球与保持架碰撞较少；轴向径向联合载荷下，球的公转角速度随接触角呈现周期性的变化，进入径向载荷区球的转速升高，而离开径向载荷区时球的转速降低，由于球在转动过程中存在加速减速过程，导致球与保持架的碰撞较为频繁，保持架的角速度也波动较大。参数化仿真的结果表明，在径向载荷区和非径向载荷区球公转速度的变化不一定，球的转速也可能会在径向载荷区降低，而在非径向载荷区升高。根据Harris在套圈控制假设下推导的球公转角速度与套圈速度之比的公式，通过定性分析可得知：外滚道控制条件下，内滚道旋转的轴承，球进入径向载荷区转速降低，而离开径向载荷区时转速升高；内滚道控制、外滚道旋转的条件下，球的公转速度有相同的变化规律，而在其它条件下，球的公转速度变化不定。以上分析与动力学的结果相吻合，说明角接触球轴承在联合载荷作用下，球的公转速度的变化不一定是通常认为的载荷增大转速升高，载荷减小转速降低，还与接触角、旋滚比和转速等因素有关。需要注意的是，虽然球的公转速度随接触角周期性变化，但幅度其实很小，为0.085%。在轴向、旋转径向负荷共同作用下，球的公转速度的变化周期减小，由于几何和工况因素的耦合，球与保持架的碰撞也较少，保持架角速度波动的大小和频率均减小。

图10(c)所示为1#球与保持架兜孔碰撞点角位置，碰撞点角位置在0°或180°上下波动，即球滞后或超前保持架的运动。碰撞点在0°附近时，保持架推球，在180°附近时球推保持架。纯轴向载荷下，由于保持架重力和离心力的作用，各球在保持架兜孔中的前后位置也会不同。球与兜孔碰撞点的滑动速度分量产生对保持架的轴向力，不同兜孔碰撞点处产生的轴向分力形成力偶作用于保持架，从而使保持架沿轴向发生摆动。轴向载荷下球在径向平面内运动，球与保持架兜孔碰撞点的位置因保持架的摆动而在0°或180°附近变动。在轴向径向联合载荷作用下，因接触角的变化，球在不同角位置处有微小的轴向位移(与保持架兜孔间隙相差两个数量级)，加上保持架本身的摆动，导致了球与兜孔碰撞点角位置在0°或180°上下波动。

图10(d)所示为1#球与保持架兜孔的碰撞力。可以看出在轴向径向联合载荷下，碰撞力较大，频率也较高，是因为在径向载荷下球有加速和减速过程，各球的转速不一致导致球与保持架更容易碰撞。而在旋转径向载荷下，由于保持架的涡动与球的转速的耦合，使球与保持架的碰撞较少。

图10(e)所示的保持架时间平均磨损率是所有兜孔的磨损率。因为是球引导保持架，保持架与套圈挡边没有碰撞，磨损主要发生在兜孔上。纯轴向载荷下保持架的磨损率最小，轴向径向联合载荷下保持架的磨损率最大，此时对应保持架的运动最不稳定，质心轨迹摆动较大，且轨道半径发散。保持架的时间平均磨损率综合反映了球与保持架碰撞力的大小和频率。

2.2 不同间隙比的结果

球与保持架兜孔间隙和保持架引导面与套圈挡边间隙是影响保持架稳定性的重要设计参数。通常用兜孔间隙与挡边间隙之比B/R进行参数化分析，得到最优的保持架结构参数。不同的间隙比对应不同的保持架引导方式，一般地B/R<1时为球引导，B/R=1时为球与套圈混合引导，B/R>1时为套圈引导。对于转速较高的仪表转子轴承，当转子中心与支承中心不重合或转子质心偏移时会产生较大的惯性负荷，相当于对轴承施加一个旋转径向负荷。转子质量一般较小(50 g)，重力产生的径向力可以忽略，轴向预紧载荷加旋转径向负荷是高速仪表转子轴承典型的工况。根据某仪表转子轴承的实际工况，轴向预紧载荷7 N，内圈转速30 000 r/min，旋转径向负荷假定为5 N。在该工况下分析了不同间隙比对保持架的运动、碰撞和磨损的影响，结果如图11所示。

图11(a)所示的保持架质心运动轨迹可知，当兜孔间隙小于挡边间隙即球引导保持架时，保持架的质心运动轨迹接近于圆形，随着间隙比的增大，保持架的质心轨迹由圆形变为多边形直至无规律的涡动，轨迹半径随之减小。说明球引导保持架时有利于形成圆形的涡动轨迹，套圈引导保持架时容易形成多边形的涡动轨迹。

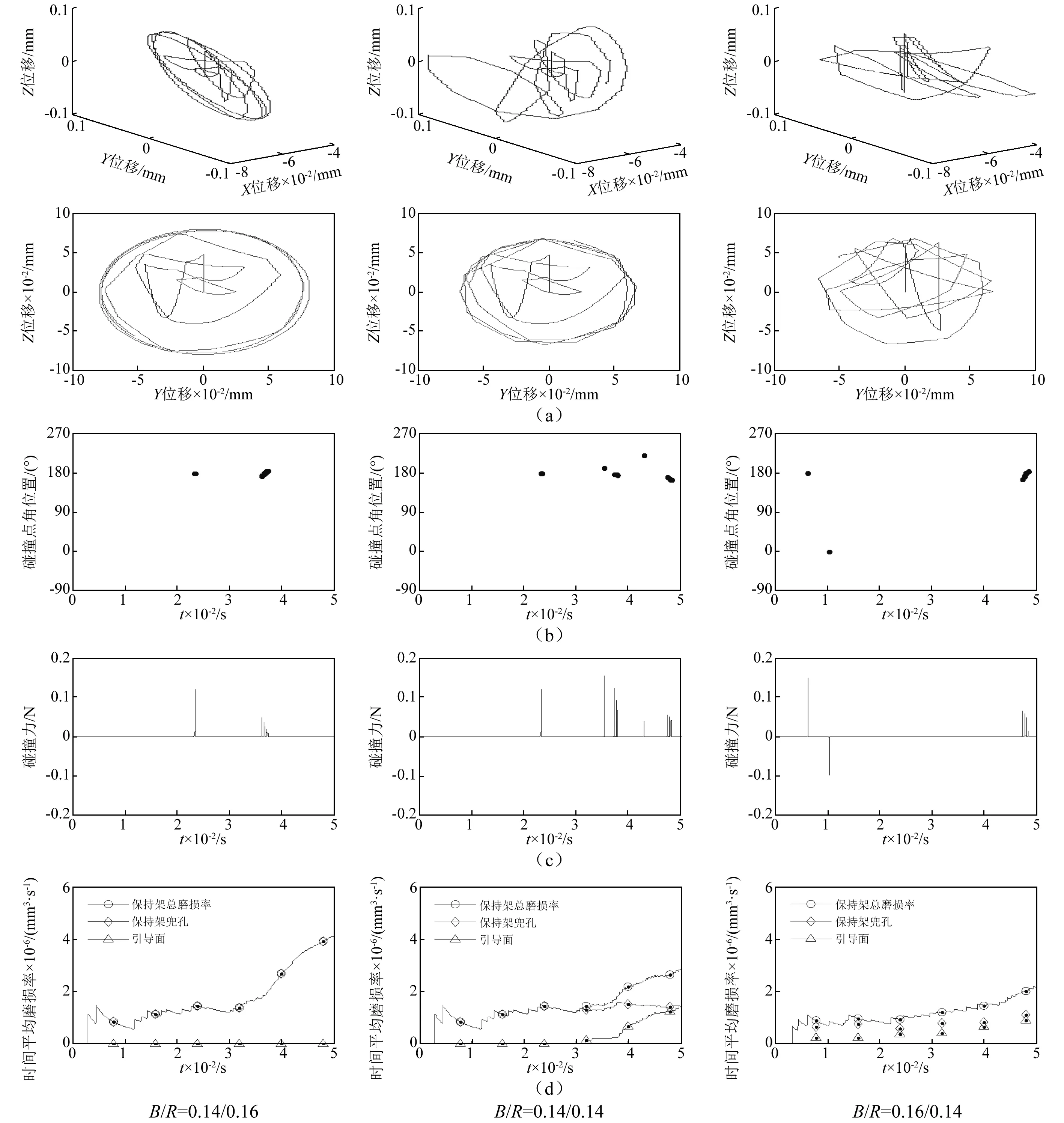
图11 轴向旋转径向负荷下不同间隙比的结果Fig.11 Results of different clearance ratio under combined axial and rotating radial load

图11(b)中，间隙比为1时球与保持架兜孔碰撞点角位置范围最大，说明保持架的轴向摆动较大，兜孔间隙较小时，保持架由球引导，保持架的离心力主要作用于球上，限制了保持架的自由摆动；而当兜孔间隙较大变为套圈引导保持架时，保持架的离心力主要作用在套圈挡边上，球与保持架的相互作用减少，保持架的摆动幅度又减小。因此，保持架由球与套圈挡边共同引导时，保持架容易发生摆动。

图11(c)所示的1#球与保持架兜孔的碰撞力可以看出，间隙比为1时，球与兜孔的碰撞较为频繁，兜孔间隙增大，碰撞力的大小变化不明显，相对于球引导，套圈引导时，球与兜孔的碰撞力稍大。

图11(d)给出了不同间隙比下保持架兜孔和引导面的磨损率分布。单看保持架兜孔的磨损率，球引导时保持架兜孔的磨损率最高，兜孔间隙增大，兜孔的磨损率降低，而保持架引导面的磨损率升高。保持架兜孔和引导面总的时间平均磨损率可以看出，随着间隙比的增大，保持架的总磨损率降低。这是因为球引导保持架时，保持架质心沿圆形轨道涡动，保持架的离心力作用于球上，增大了球与保持架兜孔之间的碰撞和摩擦。保持架由套圈挡边引导时，保持架质心没有形成稳定的涡动，其离心力较小，且有套圈挡边对保持架运动的约束会减小球与兜孔的相互作用，所以保持架兜孔和总的磨损率都较低。需要注意的是，图中所示为1#球与保持架兜孔的碰撞情况，保持架兜孔的磨损率为所有兜孔总的时间平均磨损率。

以上分析可以得出，保持架质心运动轨迹与兜孔磨损率存在对应关系。保持架质心运动轨迹为圆形且轨道半径发散，对应的兜孔磨损率较大；保持架质心轨迹呈多边形或不规则涡动且涡动半径较小时，保持架兜孔的磨损率减小。因此，从保持架磨损和能耗的观点看，圆形的质心运动轨迹未必最优。保持架质心运动轨迹越圆，说明质心涡动速度的大小稳定，波动小，但保持架涡动速度的方向不断变化，这也说明保持架与球有频繁的相互作用。保持架质心运动轨迹为多边形或无规律涡动时，虽然质心涡动速度变化较大，但球与兜孔碰撞较少，而碰撞力没有明显变化，所以保持架兜孔的磨损率较小。Meeks等分别以球与兜孔碰撞力和磨损能耗最小为准则，对保持架几何参数进行优化的结果也表明，保持架兜孔间隙与挡边间隙之比大于1时是有利的，此时对应的保持架质心运动轨迹是随机的。因此，对高速角接触球轴承保持架结构参数进行优化时，不能单纯追求保持架质心运动轨迹为圆形或涡动速度稳定，应结合球与保持架兜孔的碰撞力和磨损功耗进行综合优化。

3 结 论

利用建立的高速角接触球轴承动力学磨损数值仿真模型，分析了不同载荷工况和保持架间隙比下保持架的质心运动。从球与保持架兜孔碰撞点位置、碰撞力的大小和频率以及碰撞点切向力的方向阐释了保持架不稳定运动的机理。在给定的轴承几何、工况和润滑条件下，通过动力学仿真研究得到如下结论：

(1)纯轴向载荷下，由于保持架重力和离心力的影响，各球与保持架碰撞点的位置不同，碰撞点沿轴向的切向分力组成的力偶作用于保持架引起了保持架的轴向摆动。

(2)轴向、径向联合载荷下，球的公转角速度随接触角呈现周期性变化，但幅值较小，为0.085%。球进入和离开径向载荷区公转速度的变化与接触角、旋滚比和套圈转速有关。由于球公转一周有加速减速过程，导致球与保持架的运动不协调，容易发生碰撞，保持架的角速度波动频率较高。轴向、旋转径向联合负荷下，球的公转速度的变化周期减小，由于几何和工况因素的耦合，球与保持架的碰撞减少，保持架角速度的波动频率也减小。

(3)轴向、旋转径向联合负荷下，保持架兜孔间隙与引导面间隙之比B/R<1时，保持架质心运动轨迹接近于圆形，因为球引导保持架，保持架的离心力作用于球上，增大了球与保持架兜孔之间的碰撞和摩擦，保持架兜孔的磨损率较大；B/R=1时，保持架由球与套圈挡边共同引导，保持架质心轨迹呈多边形，保持架的轴向摆动较大，球与兜孔的碰撞频率也较高；B/R>1时，套圈引导保持架，球与保持架的相互作用减少，保持架质心涡动不规则，但球与兜孔碰撞力没有明显增大。

(4)保持架质心运动轨迹与兜孔磨损率存在对应关系，质心运动轨迹为圆形是保持架稳定运动的一种状态，但对保持架的磨损寿命不利。以保持架磨损和能耗为优化准则时，B/R>1是较优的选择。保持架兜孔的时间平均磨损率综合反映了球与兜孔碰撞力的大小和频率，可以作为保持架动态性能优化和稳定性判断的准则。