空间圈套式绳索捕获动力学建模及接触碰撞分析

张 龙

(1.中国科学院 太空应用重点实验室，北京 100094；2.中国科学院 空间应用工程与技术中心，北京 100094)

随着空间探索的不断深入，空间机械臂在空间站的组建与维护、卫星的回收与释放、在轨单元更换及目标载荷转移等方面的作用愈加凸显[1-2]。空间捕获装置作为空间机械臂最重要的一种末端执行器，其在在轨捕获任务中扮演着极其重要的角色。空间捕获装置数量众多，国际上主要航天机构都为其空间机械臂设计出相应的末端捕获装置，如德国ROTEX机械臂手爪，日本ETS-Ⅶ机械臂末端执行器，以及目前仍处在概念设计的飞网捕获装置等[3]，其结构形式、捕获原理及控制模式不尽相同，按照具体实施抓取部件的特点可将空间捕获装置分为刚性捕获装置、柔性捕获装置和刚柔耦合捕获装置。

空间圈套式绳索捕获装置属于刚柔耦合捕获装置，其捕获子系统由固定环、旋转环和三根柔性钢丝绳组成。柔性钢丝绳作为捕获元件直接与目标载荷接触，具有大容差、软接触的捕获特点，可以大大提高空间机械臂在轨捕获的成功率并降低对机械臂和目标载荷的损伤。由于其显著的优点，已经逐渐的被应用于空间捕获任务中，如加拿大SRMS末端执行器[4]，哈尔滨工业大学也已经设计出类似的捕获装置[5]。

针对空间圈套式绳索捕获过程中的动力学建模问题，已经有一些学者进行了研究。谭益松等[6]提出了一种基于扭转阻尼弹簧的平面弯曲柔性钢丝绳模型，通过在柔性钢丝绳的末端添加驱动力建立系统的力和力矩平衡方程，该方法简化了柔性钢丝绳的建模过程，但是其抗拉特性及接触碰撞特性未予考虑；李龙等[7]利用牛顿-欧拉混合坐标法建立圈套式绳索捕获过程中的动力学模型，该文中将圈套式绳索捕获机构简单的视为一个可伸缩的刚性圆环，不能全面的反映柔性钢丝绳的物理特性；潘冬等[8]将柔性钢丝绳离散成一组单元梁模型，每两个单元之间通过六维力/力矩连接以充分考虑绳索的拉伸、剪切、弯曲及扭转等变形特性，基于此建立了各离散段之间的受力与相对位移之间的关系，但是在处理接触碰撞问题时，忽略了柔性钢丝绳的抗弯特性；荣吉利等[9]采用绝对点坐标方法描述各向同性柔性钢丝绳的缠绕运动，并引入绳索与目标间的非线性动力学模型，建立了绳索与目标杆之间的刚柔耦合动力学模型，柔性钢丝绳的接触碰撞问题并未考虑；Abiko等[10-11]针对柔性钢丝绳的接触碰撞问题均作了大量的地面实物实验，通过传感器采集柔性钢丝绳接触力信息，并通过经验公式对接触力进行拟合。

针对空间圈套式绳索捕获任务，本文基于拉伸/扭转弹簧-质点的柔性钢丝绳离散模型，建立了以离散段长度、偏转角及俯仰角为变量的柔性钢丝绳动力学模型，通过引入捕获机构的约束条件，可模拟空间圈套式绳索捕获过程中柔性钢丝绳的运动状态；同时，引入虚拟弹簧的概念，分析目标载荷与柔性钢丝绳间的接触力、压缩量与柔性钢丝绳始末端距离的映射关系，建立了目标载荷与柔性钢丝绳的接触力模型，可实现对捕获过程中接触碰撞力的评估。

1 问题描述

圈套式绳索捕获装置主要由3个模块组成：绳索捕获模块，拖动模块及锁紧模块。其具体的工作原理如图1所示。绳索捕获模块的主要作用是抓捕目标载荷限制其在空间内的自由移动，该模块安装在支撑壳体上，由固定环、旋转环和三根柔性钢丝绳组成。每根柔性钢丝绳的一端安装在固定环上保持不动(称为定点)，而另外一端与旋转环相连并随之转动(称为动点)。当驱动器驱动旋转环转动时，三根柔性钢丝绳开始随之运动，形成的封闭捕获区域逐渐缩小，最终将目标载荷包围锁紧。具体的实施步骤1如下[12]：

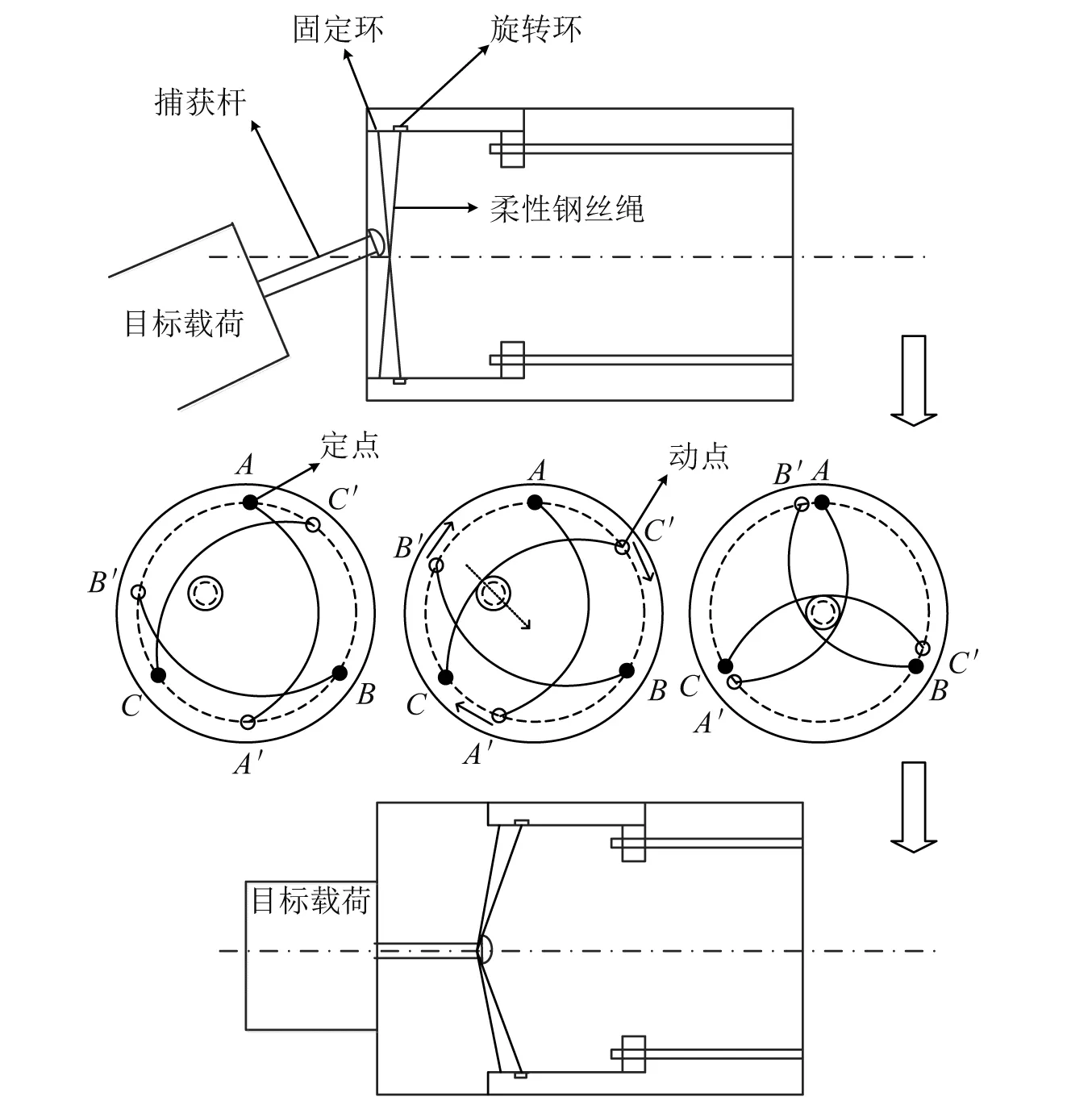
图1 空间圈套式绳索捕获过程Fig.1 The process of space snare capture

步骤1空间机械臂携带圈套式绳索捕获装置接近目标载荷，使目标载荷捕获杆进入到由三根柔性钢丝绳形成的捕获区域内；

步骤2驱动捕获装置上旋转环转动，则柔性钢丝绳的动点随着旋转环的转动而运动，使得形成的捕获区域不断的收缩，最终将限制目标载荷在空间内的自由移动，在此过程中目标载荷可能与柔性钢丝绳发生多次接触碰撞；

步骤3当捕获区域收缩完毕将目标载荷固定在捕获装置的中央，利用拖动系统拖动目标载荷，当目标载荷与捕获装置完全贴合时，利用锁紧装置将其锁紧。

2 柔性钢丝绳动力学建模

在微重力环境下，柔性钢丝绳与目标载荷之间的接触碰撞是一个非常复杂的过程，为了求得柔性钢丝绳与目标载荷之间的接触碰撞力，首先需要建立柔性钢丝绳的动力学模型。根据柔性钢丝绳在捕获过程中的具体作用和运动特点，可知其需具备两种典型的物理特性，即抗拉特性和抗弯特性。因此，需要建立兼顾抗拉和抗弯特性的柔性钢丝绳动力学模型。

2.1 数学描述

将柔性钢丝绳在空间上离散为一组依次连接的节点，节点编号由绳的一端向另一端依次增加(B1,B2,B3,…,BN)，相邻节点之间由无质量的拉伸弹簧连接，以此表现出柔性钢丝绳的抗拉特性。建模时将柔性钢丝绳所受外力集中施加在各个节点上，根据线密度通过集中质量法可确定每个节点质量

(1)

(2)

式中：mtot为柔性钢丝绳的总质量。

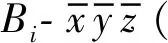
图2 柔性钢丝绳坐标系Fig.2 The coordinate systems of flexible cable

2.2 基本运动方程

(3)

(4)

式中：S(ωi)称为角速度算子矩阵，由式(4)可求得

(5)

若设ωi=[ωix,ωiy,ωiz]T，由于角速度算子矩阵元素具有反对称性质，则可定义为

(6)

(7)

对式(7)求导可得其旋转角加速度

(8)

定义第i段柔性钢丝绳的即时长度向量为li，则第i段柔性钢丝绳的速度向量可表示为

(9)

对式(9)求导可得第i段柔性钢丝绳的加速度向量

(10)

将式(3)、式(7)～式(9)代入式(10)中可得

(11)

式(11)为第i段柔性钢丝绳的加速度向量在惯性系下的表示，其计算结果相当复杂，二阶导数项耦合在一起很难对其进行有效的分离，将其转换到第i个动坐标系下可得其极简的表达式，结果为

(12)

以上从运动学层面建立了柔性钢丝绳的运动方程，下面从动力学角度对其运动特性进行描述。首先对节点Bi,Bi+1进行受力分析，如图3所示。

图3 节点Bi,Bi+1处的受力情况Fig.3 Force analysis of nodes Bi,Bi+1

依据牛顿第二定律可得第i段柔性钢丝绳的加速度与所受外力的关系为

(13)

(14)

(15)

将式(12)和式(13)联立即可得到以偏转角ϑ、俯仰角φ及柔性钢丝绳离散段拉伸长度l为变量的柔性钢丝绳动力学方程，通过分离二阶导数项可得其最终表达式为

(16)

式中：xr=[ϑi,φi,li]T为柔性钢丝绳的变量；Hr为柔性钢丝绳系统惯性矩阵；Cr为系统的非线性项；Pr为系统的势能项；Fr为等效外力项。其中，i=1～N-1。若i=1，所有下标为i-1的变量取值均为0，若i=N-1，Ti+1,ϑi+1,φi+1则为0。至此，柔性钢丝绳的基本运动方程已经建立，由于拉伸弹簧的引入该模型可以反映出柔性钢丝绳的抗拉特性。

2.3 抗弯特性等效

对于空间圈套式绳索捕获来说，为保证由柔性钢丝绳形成的捕获区域具有尽量大的容差性，钢丝绳的抗弯特性显得很重要。柔性钢丝绳的抗弯特性可以使得捕获机构拥有较大的有效捕获区域(见图4)，上一节中推导的柔性钢丝绳运动方程中，拉伸弹簧用来模拟柔性钢丝绳的抗拉特性，本节中在每个节点处加装一个扭转弹簧以模拟柔性钢丝绳的抗弯特性。

图4 圈套式绳索捕获有效捕获区域Fig.4 Effective capture region of snare capture

每个节点处的弯曲力矩大小可由式(17)计算

(17)

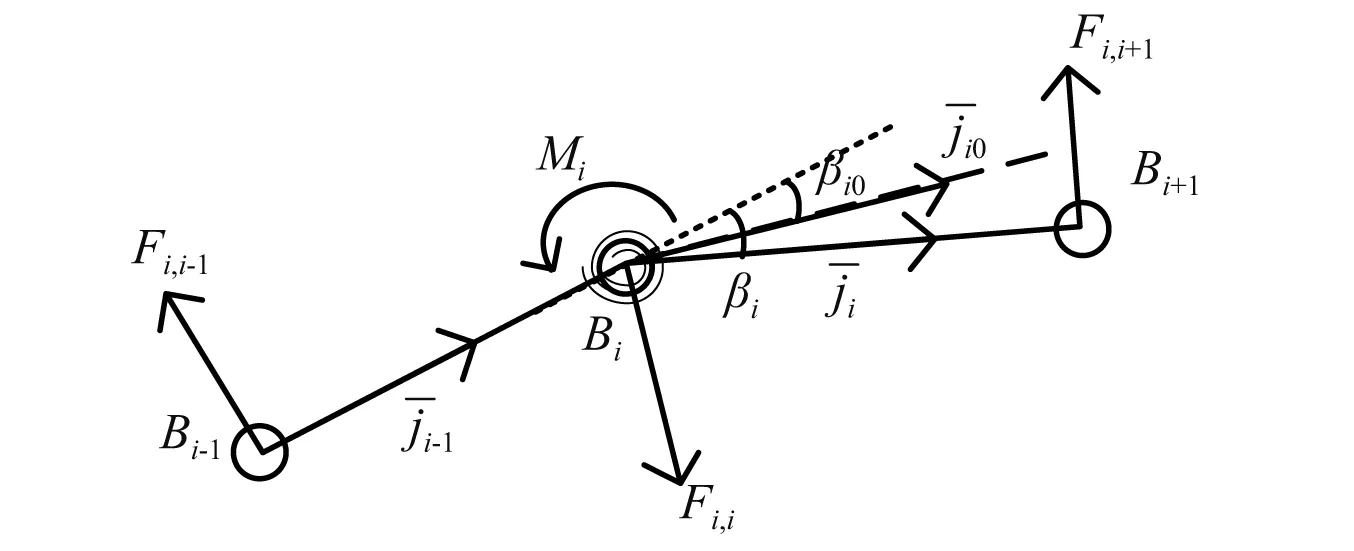
图5 柔性钢丝绳弯矩结构等效力Fig.5 The equivalent structural forces of bending moment

等效结构力在平衡节点处弯矩的同时，还需要满足自身结构力的平衡，即满足

Fi,i=-(Fi,i-1+Fi,i+1)

(18)

(19)

式中：i=1～N，若i=1，则Fi,i-1=0；若i=N，则Fi,i+1=0；ei,i-1,ei,i+1分别为Fi,i-1,Fi,i+1的单位方向向量可由式(20)计算

(20)

以上计算所得出弯矩等效结构力Fi,i-1，Fi,i和Fi,i+1可以作为外力直接代入式(16)中对柔性钢丝绳的运动状态进行求解。至此便建立了完整的柔性钢丝绳动力学方程，基于拉伸和扭转弹簧该模型可以反映出柔性钢丝绳在圈套式绳索捕获过程中基本的抗拉和抗弯曲的物理特性。

3 圈套式绳索捕获约束分析

假设圈套式绳索捕获机构的固定环和旋转环处于同一平面上，且半径为Rcm。初始状态下柔性钢丝绳AA′的A端安装在固定环上，A′端连接在旋转环上，相邻离散段之间的初始夹角为β1,β2,…,βN-1(见图6)，其初始处于静态平衡状态。为求得柔性钢丝绳的初始状态，对其进行受力分析。

图6 柔性钢丝绳初始位置Fig.6 Initial position of flexible cable

依据图7，对各个节点可列平衡方程

-Ti-1+Ti+Fi,i+Fi-1,i+Fi+1,i=0

(21)

式中：i=2～N-1；Ti-1,Ti为柔性钢丝绳第i-1段和第i段产生的弹性拉力；Fi,i,Fi-1,i,Fi+1,i为Bi，Bi-1和Bi+1处扭转弹簧在节点Bi处产生的等效结构力。由于式(21)可以拆分为y和z方向上两组标量方程组，因此共建立了2(N-2)个静态力平衡方程。此外，从几何约束的角度分析，由于柔性钢丝绳AA′在平面yz内运动，可令ϑi=0，则以下两个方程可以建立

(22)

式中：dse为柔性钢丝绳始末端的距离。

图7 柔性钢丝绳初始状态受力分析Fig.7 Initial force analysis of flexible cable

联立式(21)和式(22)可得到2(N-1)个方程，同时易知βi=(φi-1-φi)，则基础未知变量(li,φi)个数同样为2(N-1)个，方程组可解。初始状态下的拉伸和弯曲预紧力即可求得

(23)

Mi 0=ktor(βi-βi 0)

(24)

以上便对柔性钢丝绳在圈套式绳索捕获机构中的约束及初始状态进行了分析，同时，由于捕获装置的结构特点，动点A′需要跟随旋转环旋转，对于定点A来说，此处由于是铰接没有弯曲力矩产生。

4 柔性钢丝绳接触动力学建模

4.1 接触碰撞假设

空间微重力环境下，柔性钢丝绳与目标载荷之间的接触碰撞是一个非常复杂的过程，精确的接触碰撞动力学模型很难获得，为了简化建模过程，做了以下几个接触碰撞假设：

(1)柔性钢丝绳与目标载荷之间仅发生单点接触，并且接触力仅施加在节点上，事实上，当柔性钢丝绳离散模型划分的很细、节点足够多的时候该种假设是易实现的；

(2)为保证捕获过程的安全性及操作的可靠性，假设柔性钢丝绳与目标载荷之间的相对接触速度很小；

(3)假设接触碰撞这段极小时间内接触碰撞力的方向并未发生改变；

(4)与法向接触碰撞力相比，切向的摩擦力可以忽略不计。

4.2 虚拟弹簧

当柔性钢丝绳受到外力作用时，根据其受力时的反应状态，可以假定在柔性钢丝绳与支撑壳体之间存在一根虚拟的弹簧(见图8)，弹簧的一端连接在柔性钢丝绳的节点上，另一端连接在支撑壳体上。由于虚拟弹簧的刚度系数不是常量，接触碰撞力不能简单的依据Hertz-阻尼模型计算。经分析可知虚拟弹簧的刚度系数与压入深度δv及柔性钢丝绳始末端的距离dse有关，其中压入深度δv定义为柔性钢丝绳从初始位置压入至当前位置在接触方向上移动的距离。

图8 柔性钢丝绳接触碰撞虚拟弹簧模型Fig.8 The virtual spring model of flexible cable

假设接触碰撞发生在节点n上，受力如图9所示。依次针对节点2～(N-1)建立力的静态平衡方程

(25)

式中：Fc为施加在节点n上的外力。

图9 柔性钢丝绳受力分析(含接触力)Fig.9 Force analysis of flexible cable(considering contact force)

式(25)结合几何约束式(22)可得柔性钢丝绳在存在外力情况下的平衡方程组。当给出一组Fc和dse时，则对应的压入深度δv即可求得。柔性钢丝绳的接触情况可与弹簧的接触进行类比，但不同的是柔性钢丝绳在接触过程中的刚度不是唯一不变的，它是与压入深度、柔性钢丝绳始末端距离有关的量。定义虚拟弹簧的刚度系数为接触点处法向压力与对应压入深度的比值，可采用以下步骤对其进行求解：

步骤1首先设定初始取值范围dse∈[dmin,dmax]，Fc∈[Fmin,Fmax]，其中，dse的取值范围由机构的约束决定；而对于外力Fc，其施加的力方向为各个节点处的法向方向，其大小由一个试探性的过程最终确定，最小值为0，假设最大值为FA；

步骤2按一定的间隔在取值范围内各自取出一组值，[dmin,ds1,ds2,…,dmax]∈R1×m，[0,Fn1,Fn2,…,FA]∈R1×n，dmin

Fc=f(δv)+g(dse)+h(δv,dse)

(26)

式中：f(δv),g(dse)分别为以δv,dse为单变量的多项式函数;h(δv,dse)为多变量耦合函数。值得注意的是，当单一曲面函数拟合精度不足时，可以采用分段函数对数据进行拟合。

依据定义可得出虚拟弹簧接触刚度系数的表达式

(27)

步骤3在空间圈套式绳索捕获过程中，当压入深度、柔性钢丝绳始末端距离已知时，虚拟弹簧接触刚度系数即可由式(27)求得。更进一步的，目标载荷与柔性钢丝绳之间的动态接触碰撞力即可依据Hertz-阻尼模型计算

(28)

值得注意的是，提出的采用多项式函数拟合方法求取柔性钢丝绳虚拟弹簧的接触刚度系数，其具有一定的适用范围，即dse∈[dmin,dmax]，Fc∈[Fmin,Fmax]。在空间圈套式绳索捕获过程中只有上述两个变量在此范围内时，其计算精度才能保证。如果发现接触碰撞过程中的最大压缩位置δv max处的接触力Fc max=kvδv max大于已经设定拟合范围的上限值FA时，那么需要重新设定上限值为FB以使得FB>Fc max，然后重复上述计算过程，直到计算结果满足约束条件。为避免类似的重复性工作，在初始阶段可以将Fc的上限值设置的尽量大，但是这会使得在数据拟合阶段耗费较多的时间。

5 仿真实验

5.1 柔性钢丝绳运动状态仿真

设定圈套式绳索捕获机构的固定环与旋转环的内径均为Rcm=0.5 m，柔性钢丝绳初始总长度为ltot=1 m，线密度为ρlin=0.344 kg/m。将柔性钢丝绳离散为50段共计51个节点，各节点处的拉伸弹簧及扭转弹簧的刚度系数和阻尼系数分别为ktes=5×104N/m，ctes=1×102N·s/m，ktor=1×103N·m/rad，ctor=1 N·m·s/rad。设柔性钢丝绳各个节段之间的初始弯曲角度为βi 0=1°。

由上述驱动引起的柔性钢丝绳运动状态如图10所示，图10(a)表示单根柔性钢丝绳的运动状态，图10(b)则表示圈套式绳索捕获过程中三根柔性钢丝绳相互配合的整体运动状态，图中黑色圆圈代表柔性钢丝绳的固定点，白色圆圈代表动点。从图10中可以看到柔性钢丝绳的动点处由于与旋转环固连，会随着旋转环做圆弧运动进而带动整个柔性钢丝绳运动形成捕获区域。

图10 柔性钢丝绳的运动状态Fig.10 The motion of flexible cable

5.2 圈套式绳索捕获接触碰撞分析

设定目标载荷的质量为mtar=20 kg，末端坐标系下初始位置Ptar=[0,0.20,0.30] m，初始速度Vtar=[0,0.05,0.01] m/s。检测到目标载荷首先与柔性钢丝绳AA′上的节点17接触(节点编号从固定点A开始)。依据文中定义可得节点17处的虚拟弹簧接触刚度系数拟合方程为

(29)

式中：p00～p22为变量系数，取值如表1所示。

表1 节点17处接触刚度拟合方程系数Tab.1 Coefficient of fitting equation of node 17 contact stiffness

设定阻尼系数为cv=1 N·m·s/rad，则目标载荷与柔性钢丝绳接触过程中的动态接触力可由式(28)计算。接下来目标载荷与柔性钢丝绳BB′，CC′的接触碰撞采用上述类似的方法，在已知柔性钢丝绳始末端距离dse及压入深度δv的情况下，即可求得柔性钢丝绳与目标载荷之间的接触碰撞力曲线，整个捕获运动过程如图11所示。图12为柔性钢丝绳与目标载荷接触碰撞时目标载荷受到的碰撞力，目标载荷第一次与柔性钢丝绳AA′接触发生在约1.10 s，持续时间约为0.79 s，-y和-z方向的最大接触碰撞力为2.78 N和2.37 N。第二次与柔性钢丝绳BB′的第22个节点发生碰撞在约15.51 s，持续时间约为0.75 s，y和z方向的最大接触碰撞力为0.17 N和4.24 N。第三次与柔性钢丝绳CC′的第31个节点发生碰撞在约29.12 s，持续时间约为0.90 s，y和-z方向的最大碰撞力为2.36 N和2.65 N。

图11 圈套式绳索捕获接触碰撞过程Fig.11 The contact during snare capture

图12 圈套式绳索捕获过程中接触力Fig.12 The contact force during snare capture

6 结 论

空间圈套式绳索捕获装置由于具有大捕获容差、高刚性连接及软接触的优点，已经逐渐被应用于太空中大型航天器的捕获任务中。本文针对空间圈套式绳索捕获动力学及接触碰撞问题进行研究，提出了一种基于拉伸/扭转弹簧-质点的柔性钢丝绳动力学建模方法，可以表现出柔性钢丝绳抗拉及抗弯等基本物理特性，可以模拟空间圈套式绳索捕获过程中柔性钢丝绳的运动情况；提出了一种基于虚拟弹簧的柔性钢丝绳接触力建模方法，可以计算目标载荷与柔性钢丝绳间的接触碰撞力。研究成果可以实现对空间圈套式绳索捕获过程的预演，及时发现捕获任务中潜在的问题，避免风险。