基于最优决策的国际铁路多式联运合作伙伴选择模型

刘 澜，黄 豪

(1.西南交通大学 交通运输与物流学院，四川 成都 610031；2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 610031)

随着“一带一路”倡议的推进，我国加快了与周边国家物流通道建设的进程。作为陆上运输大通道，国际铁路的建设和发展为国际多式联运的开展打下了坚实的基础。现阶段，我国已广泛开展对中亚、欧洲等地的公铁、铁水集装箱多式联运[1]。在多式联运联盟构建过程中，多式联运合作伙伴的选择是联盟中主体企业最为关注的问题之一[2]。然而，大多数企业在发展多式联运业务时，对合作伙伴的选择缺乏科学依据[3]，合作伙伴之间的不兼容不仅仅会增加各企业的成本，更会严重影响多式联运的效率。因此，为了促进“一带一路”倡议下国际铁路多式联运的发展，研究其合作伙伴选择模型具有重要的现实意义。

国内外学者关于合作伙伴选择问题的研究主要集中于“合作伙伴选择影响因素和指标”及“合作伙伴选择方法”2个方面。Ohmae[4]提出了适用于一般战略联盟合作伙伴选择的4项影响因素：信任度和理解度、联盟高柔性、企业文化协同能力、互益程度。Michael D.Hutt[5]通过实例研究提出了影响合作伙伴行为的3个主要因素：信任、关系承诺以及兼容性。在合作伙伴选择方法方面，S.Lozano[6]运用DEA法对横向合作伙伴的选择进行了研究，谢军[7]对国内外有关供应链合作伙伴选择方法的研究进行了综述，总结了合作伙伴选择的10种方法，但基本上都为单一评价方法。近年来，根据不同方法的优劣势进行组合成为了新的研究趋势，如徐红梅[8]、肖赟[9]、Xiao[10]运用多种方法组合对合作伙伴选择问题进行了研究。学者们在多式联运合作伙伴选择方面研究较少，陈宇[11]以运营成本、运营时间和运营风险的最小化为目标函数建立基于遗传算法的集装箱多式联运合作伙伴选择的模型，刘舰[12]运用决策理论和博弈论设计了多式联运分运人2阶段选择模型。

从国内外研究可知，国际铁路多式联运合作伙伴选择问题还未被深入探讨过，且对于多式联运合作伙伴的选择问题往往只是考虑公铁水企业的合作，而基于国际铁路发展多式联运的实际需要，应发挥其具有第三方物流公司的货源“蓄水池”的作用[1]。本文借鉴以往的研究成果，以构建国际铁路的公铁水及第三方物流多式联运合作伙伴选择模型为目的，通过引入对合作伙伴选择步骤的分析，将模型构建与选择步骤相对应，依次通过AHP-FCE法对潜在合作伙伴进行综合评价，并将综合评价值作为输入值代入DEA法中，对潜在合作伙伴进行效率评价并选择出可行合作伙伴，最后构建综合考虑运营成本及运输时间的0-1整数规划模型对可行合作伙伴进行优化组合。通过对中老铁路设计算例分析，以验证模型在多式联运合作伙伴选择中的可行性及优越性。

1 国际铁路多式联运合作伙伴选择步骤

通常来说，可以将国际铁路合作伙伴选择的步骤分为合作伙伴选择准备、合作伙伴优选以及合作伙伴优化组合3个阶段，如图1所示。

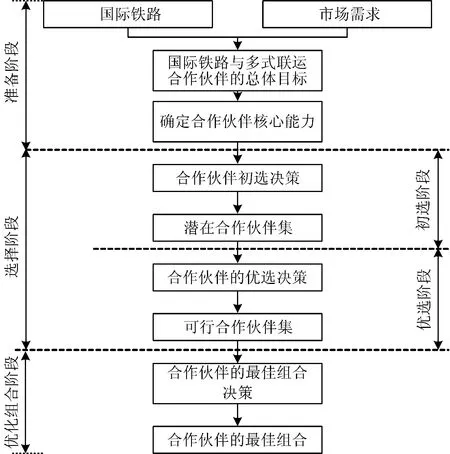
图1 合作伙伴选择步骤

合作伙伴选择准备阶段是指国际铁路在社会市场需求的驱动下，制定多式联运的总体目标，确定合作伙伴应该具备的核心能力。合作伙伴的选择阶段可分为初选阶段和优选阶段，经过初选和优选决策选择潜在合作伙伴集以及可行合作伙伴集。合作伙伴优化组合阶段是指通过最佳组合决策，在可行合作伙伴集合的基础上进行优化组合，选出使整体效益能达到最优的组合方案。

2 多式联运合作伙伴选择模型构建

根据合作伙伴选择步骤中的初选、优选以及优化组合3阶段分别构建评价及选择模型，依次选择出潜在合作伙伴集、可行合作伙伴集以及合作伙伴最佳组合。

2.1 AHP-FCE法对合作伙伴进行综合评价

层次分析法(Analytic Hierarchy Process，AHP法)是一种定性与定量分析相结合的多目标决策分析方法[13]。模糊综合评判法(Fuzzy Comprehensive Evaluation，FCE法)是在模糊数学的隶属度理论基础上，将模糊和难以量化的因素定量化后进行综合评价的方法[14]。AHP—FCE是将层次分析法和综合模糊评判法联合起来形成的评价方法[15]，具体步骤如下所示。

1)建立评价指标体系

结合既有研究的经验，基于多式联运的特点，将多式联运联盟潜在合作伙伴评价指标体系U进行分类，分为m个因素子集Ui，i=1，2，…，m，得到相应的准则层U={U1，U2，U3，U4}={基于情况，兼容性，适应性，多式联运技术指标}。其中，对应每1个Ui又有个因素，得到对应得指标集Ui={Ui1，Ui2，…，Uin}，如U2={U21，U22}={企业文化兼容性，战略目标兼容性}，具体如图2所示。

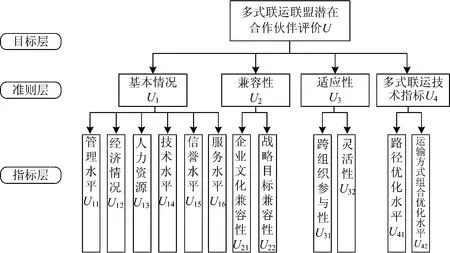
图2 多式联运合作伙伴综合评价指标体系

2)基于AHP法的指标权重确定

以准则层为例，依据标度理论[13]，由专家调查法对多式联运合作伙伴综合评价指标体系中同一层次的不同因素进行两两比较，构造判断矩阵

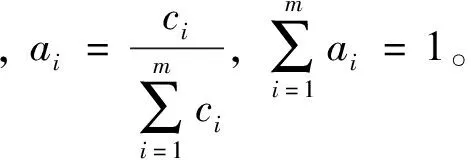
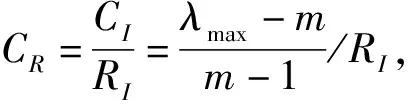
一般认为，若CR<0.1，可接受一致性检验，否则修正判断矩阵。

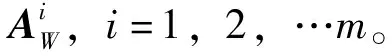
3)FCE法对企业进行综合评价

首先需确定评语集V={v1，v2，…，vk}，评语集代表了对每个指标所做出的评价程度，如V={好，较好，良，较差，差}，与评语集对应的有评分向量G={g1，g2，…，gk}，本文取G={1，0.75，0.5，0.25，0}。

依据构建的评语集，由专家对各指标层进行等级判定，并根据各评价等级的人数比例形成隶属矩阵Ri为

对指标层中的各类进行模糊综合评价，可得到评判矩阵Bi为

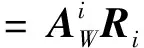
=(bi1,bi2, …，bik)

形成隶属矩阵R=(B1，B2，…，Bm)T，考虑准则层各因素权重，得到综合评价向量D为

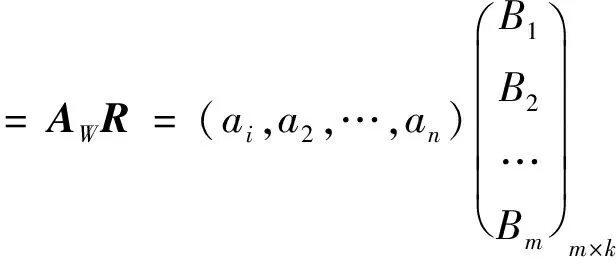
=(d1，d2，…，dk)

最后，求得综合评价分数F=DGT。

依据上述AHP-FCE法，依次对多式联运联盟潜在合作伙伴进行综合评价。

2.2 DEA法分析潜在合作伙伴的相对效率

数据包络分析(Data Envelopment Analysis)简称DEA法，DEA法是运用数学规划模型对具有多个输入和输出的“单位”(称为决策单元，简记为DMU)进行评价，判断其相对有效性(称为DEA有效)[16]。

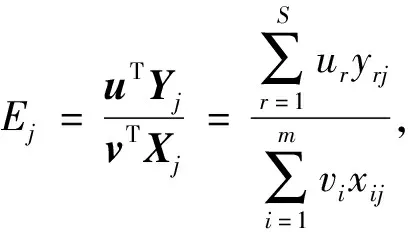
假设对第j0个潜在合作伙伴进行效率评价，根据CCR模型建立相关线性规划模型来评定该潜在合作伙伴的效率。

minE

(2)

s.t.

(3)

(4)

(5)

E，λj≥0

(6)

式中：λj为输入输出的加权系数。

依据上述CCR模型，依次对经过AHP-FCE法选出的潜在合作伙伴建立相关模型，评价各自的相对效率，筛选出可行合作伙伴集。

2.3 0-1整数规划优化组合

为了使多式联运联盟达到整体最优，用0-1整数规划选择1组最优合作伙伴组合。

考虑可行合作伙伴的个体内在成本、个体内在运输时间以及与其他企业的连接成本、连接时间，以多式联运联盟总运营成本及运输时间与最小值偏差最小为目标函数，建立0-1整数规划模型为

minZ=λ1V1+λ2V2

(7)

s.t.

V1=Cmin

(8)

V2=Tmin

(9)

(10)

(11)

λ1，λ2，V1，V2>0

(12)

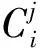
V1和V2为偏移系数，λ1和λ2为其权重。

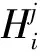
依据上述模型，即可在可行合作伙伴集的基础上筛选出最优合作伙伴集合。

3 算例分析

中老铁路是连接我国与东南亚国家的重要运输通道，其在中国段的起点为昆明市，依附昆明国际陆港，充分发挥国际陆港对多种运输方式的集合作用以及对物流服务的提升作用，开展公铁水多式联运。借鉴欧美国家铁路发展多式联运的先进经验[1]，考虑第三方物流企业的加入。根据市场需求和对相关企业的了解，选取了2家公路运输企业，2家水路运输企业和6家第三方物流企业。由于公路运输企业和水路运输企业数目小，选择较为容易，第三方物流企业数目众多，需从中选出效率相对较高的第三方物流企业，然后将选出的第三方物流企业与公路运输和水路运输企业优化组合，选出最优合作伙伴集合。

3.1 AHP-FCE法对潜在合作伙伴进行综合评价

依据多式联运合作伙伴综合评价指标体系，构造相应判断矩阵并确定权重如表1—表5所示。

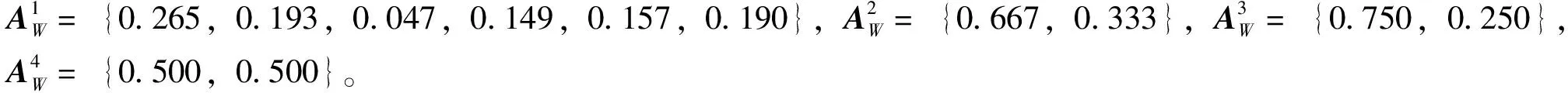
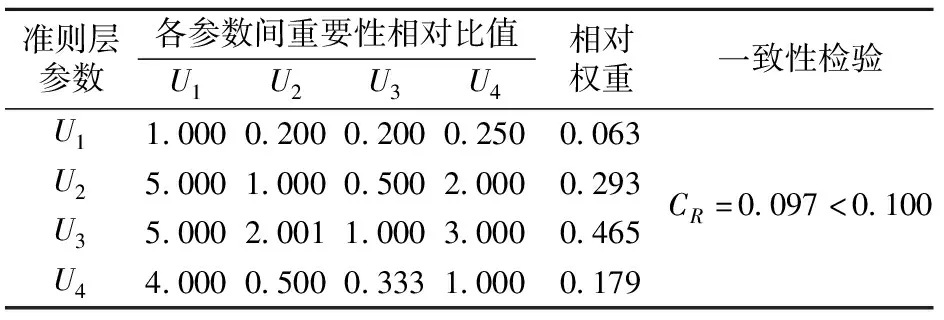
表1 准则层相对权重确定

表2 U1指标层相对权重确定

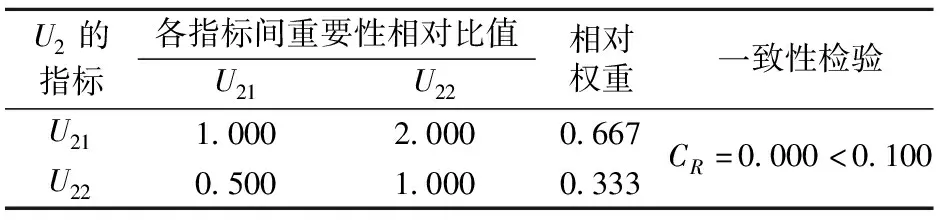
表3 U2指标层相对权重确定

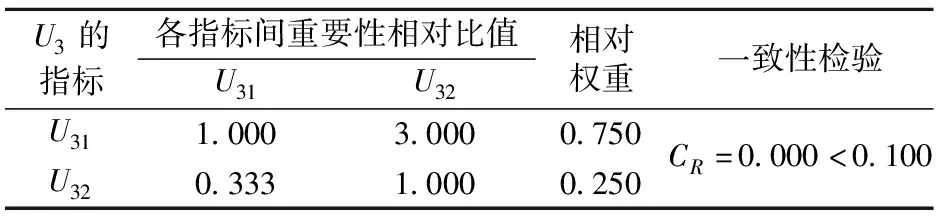
表4 U3指标层相对权重确定

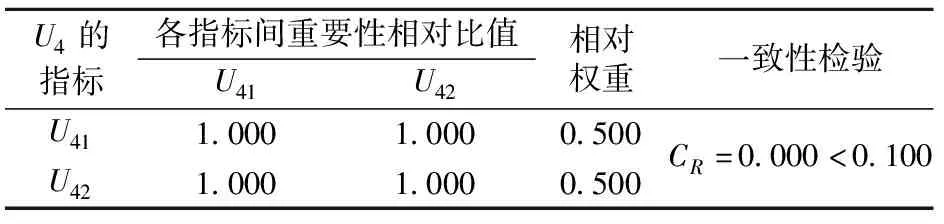
表5 U4指标层相对权重确定

以企业编号为1的第三方物流企业为例，假设由专家对该企业各指标层进行等级判定，得到隶属矩阵为

则相应的评判矩阵Bi为

则隶属矩阵R为

综合评价向量D=AWR=(0.379，0.258，0.201，0.141，0.032)

则1号第三方物流企业的综合评价分数F=DGT=0.708。

同理，依次求得其余第三方物流企业的综合评价分数如表6所示。

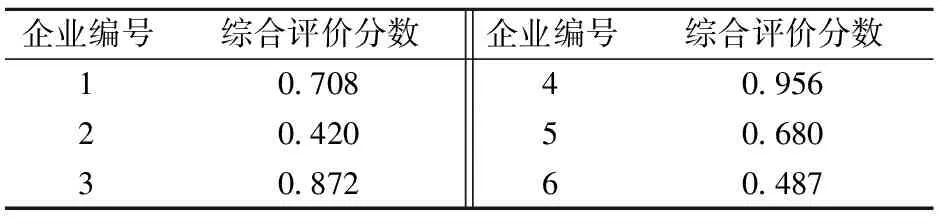
表6 潜在第三方物流企业的综合评价分数值

从表6可知，第三方物流企业4的综合评价分数明显高于其它企业，若只采用AHP-FCE法选择合作伙伴，无疑将选择第三方物流企业4作为多式联运联盟的主体企业之一。但此处不对第三方物流企业进行筛选处理，而是将其评价结果代入DEA法中进行效率分析。

3.2 DEA法分析潜在合作伙伴的相对效率

DEA线性规划模型中选择的输入输出量指标及其数据如表7所示。

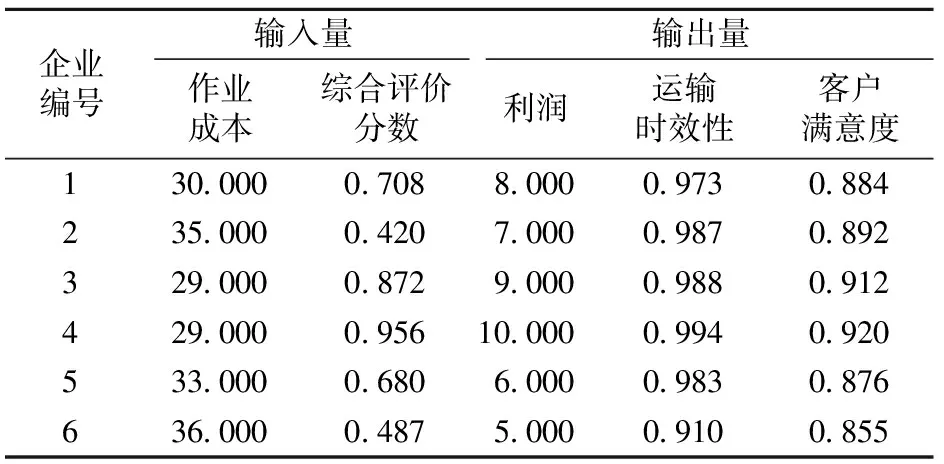
表7 潜在第三方物流企业的指标值

根据DEA线性规划模型，通过Lingo软件计算出各个第三方物流企业的相对效率，如表8所示。

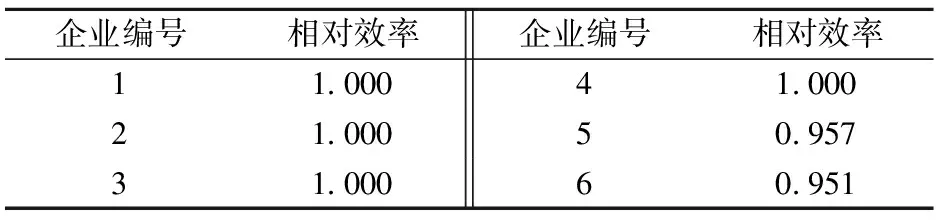
表8 潜在第三方物流企业的相对效率值

从表8可知，第三方物流企业1，2，3，4为DEA有效单元，因此选择企业1，2，3，4作为可行合作伙伴进入下一步规划求解过程。

3.3 0-1整数规划优化组合

给出连接成本及连接时间矩阵：R表示中老铁路，G1和G2表示2家公路运输企业，S1和S2表示2家水路运输企业，L1，L2，L3和L4分别表示第1，2，3，4个第三方物流运输企业。由于每种核心能力的企业只选择1家，因此同种核心能力的企业间的连接成本、连接时间为M,M为足够大的正数。可行合作伙伴间连接成本及连接时间矩阵如表9和表10所示。

根据上文0-1整数规划模型，因为H中老铁路=1，可以不考虑中老铁路内在成本及运输时间在此模型中的影响，因此有各可行合作伙伴内在成本及运输时间如表11所示。

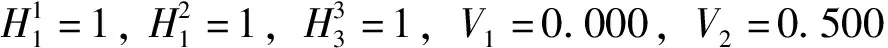
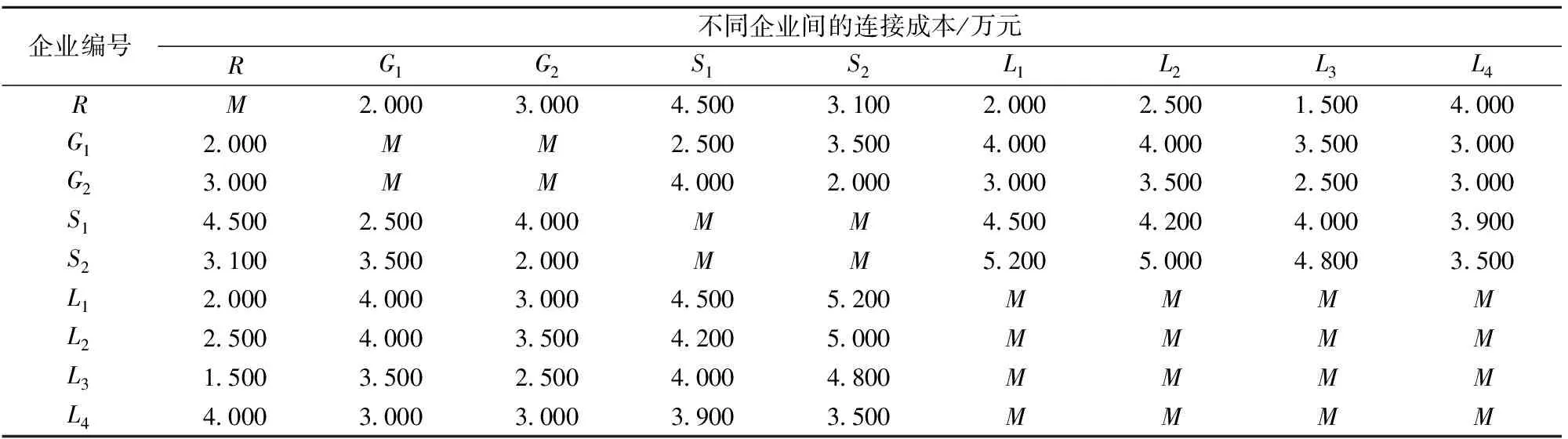
表9 可行合作伙伴间连接成本矩阵

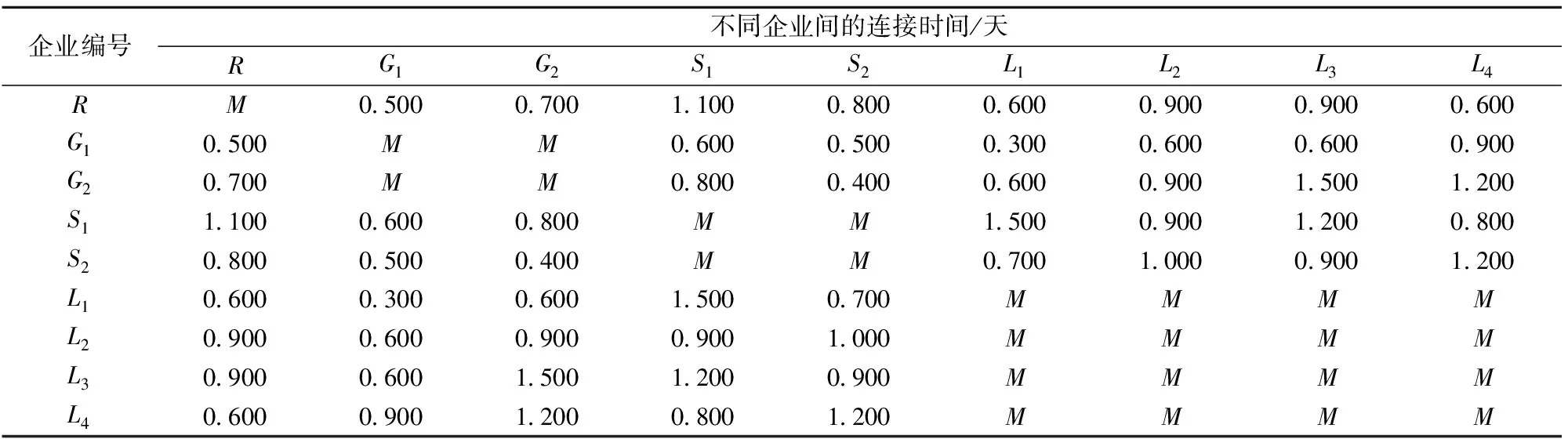
表10 可行合作伙伴间连接时间矩阵

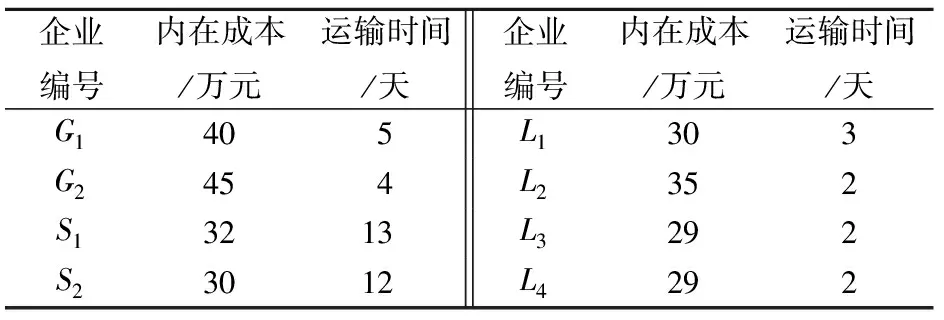
表11 各可行合作伙伴的内在成本及内在运输时间

经过0-1整数规划对合作伙伴进行优化组合后选择了L3，即第3个第三方物流企业，其在AHP-FCE评价中的综合评价分数为0.872，低于L4的综合评价分数。若仅仅通过AHP-FCE评价选择L4作为合作伙伴，此时的多式联运联盟较最优组合总运营成本将增加0.700万元，总运输时间将增加0.800天，即V1=0.700，V2=1.300，Z=0.880。

4 结 语

本文通过引入对合作伙伴选择步骤的分析，将模型构建与选择步骤相对应，提出了基于AHP-FCE，DEA和0-1整数规划的多式联运合作伙伴选择模型。运用AHP-FCE法对多联运合作伙伴进行综合评价，在AHP层次分析结构模型中既考虑了企业的基本情况，又考虑了企业加入联盟后的兼容性、灵活性及多式联运指标的好坏，将AHP法与FCE法结合既能体现出评价过程的模糊性，又能减少个人臆断带来的弊端，提高评价的可靠性。将AHP-FCE法的综合素质评价结果代入DEA法中，选择效率相对较高的可行合作伙伴集。综合考虑多式联运联盟总运营成本及总运输时间，构建0-1整数规划对多式联运合作伙伴进行优化组合，使得多式联运联盟总运营成本及运输时间与最小值偏差达到最小。本文以中老铁路为研究对象，考虑第三方物流企业加入的国际铁路公铁水及第三方物流多式联运合作伙伴选择问题。采用本文模型对中老铁路合作伙伴进行了选择，结果证明了模型的可行性，通过与单阶段合作伙伴选择模型(AHP-FCE评价选择)的对比，突出了本文模型的优越性。