基于POT理论的城市桥梁车辆荷载效应研究
2019-10-19姜福香崔佳庆周均法
王 宁,姜福香,崔佳庆,周均法
(青岛理工大学 土木工程学院 青岛市 266033)
0 引言
随着经济的高速发展,城市车辆荷载在车流量、车重等方面都呈现出了上升的趋势,这一结果必然导致车辆荷载效应的增大,车辆荷载效应又作为桥梁工作者关心的重要指标之一。因此,城市车辆荷载效应的研究就显得尤为重要。
“公路桥梁车辆荷载研究”课题组基于测得车辆荷载效应截口分布,假设“一天代表一年”并极值外推得到了车辆荷载效应标准值;贡金鑫、李文杰等人[1-2]利用某函数对车辆荷载效应截口分布进行拟合,采用上述同样的假设,并进行了极值外推。但这种假设虽有一定理论基础,其精确度还需进一步研究。Christian Cremona等人[3-5]利用Rice公式对车辆荷载效应进行极值外推,但是Rice公式假设荷载效应为平稳高斯过程,这种假设对结果的正确性影响程度如何需要进一步研究。结合国内外对比发现,对车辆荷载效应进行研究,车辆荷载效应的尾部数据对外推值的精确性有着重要的影响,因此,选取了更能反应尾部数据的POT理论[6-7]对车辆荷载效应进行研究,此理论在水文、金融等领域得到了广泛的应用[8]。
借用Matlab编程软件,运用蒙特卡洛法模拟出随机荷载流并进行影响线加载计算,得出各跨径简支梁(10~60m)车辆荷载效应样本数据,并在此基础上进行极值外推,得到不同设计基准期内(10a~100a)外推值,并与《城市桥梁设计规范CJJ11-2011》[9]中城市-A级值作对比分析。
1 调查地区车辆荷载参数
1.1 车辆荷载模型及比例
青岛市环湾大桥双埠立交桥是设计等级为城市A级的重要桥梁,是连接主城区和高新区、城阳工业区的主要交通节点。通过现场调研、视频监控等途径,获取该桥上全天为期一个月的车流量信息,总车流量基本维持在18553~21470辆/d,其中快车道为6318~7914辆/d,中间车道685~9897辆/d,慢车道749~4658辆/d。利用加权平均法,分析依据车辆手册调查得到的各种车型数据(前悬、轴距、后悬和轴重分配比例),提出了7种车辆荷载模型及各车道车型所占比例,见表1。
1.2 车重分布拟合
分析发现,7种类型车辆的车重均为多峰正态分布,这与其他学者[10-11]研究的结论一致。在此仅以M6、M7两种车型车重为例说明,见图1和图2。根据K-S检验法和最优拟合发现,利用三峰正态分布分别对M6和M7进行拟合可以达到良好的拟合效果。7种车型分布参数见表2,其中,μ、σ、ρ分别为多峰正态分布参数中平均值、标准差、权重系数。
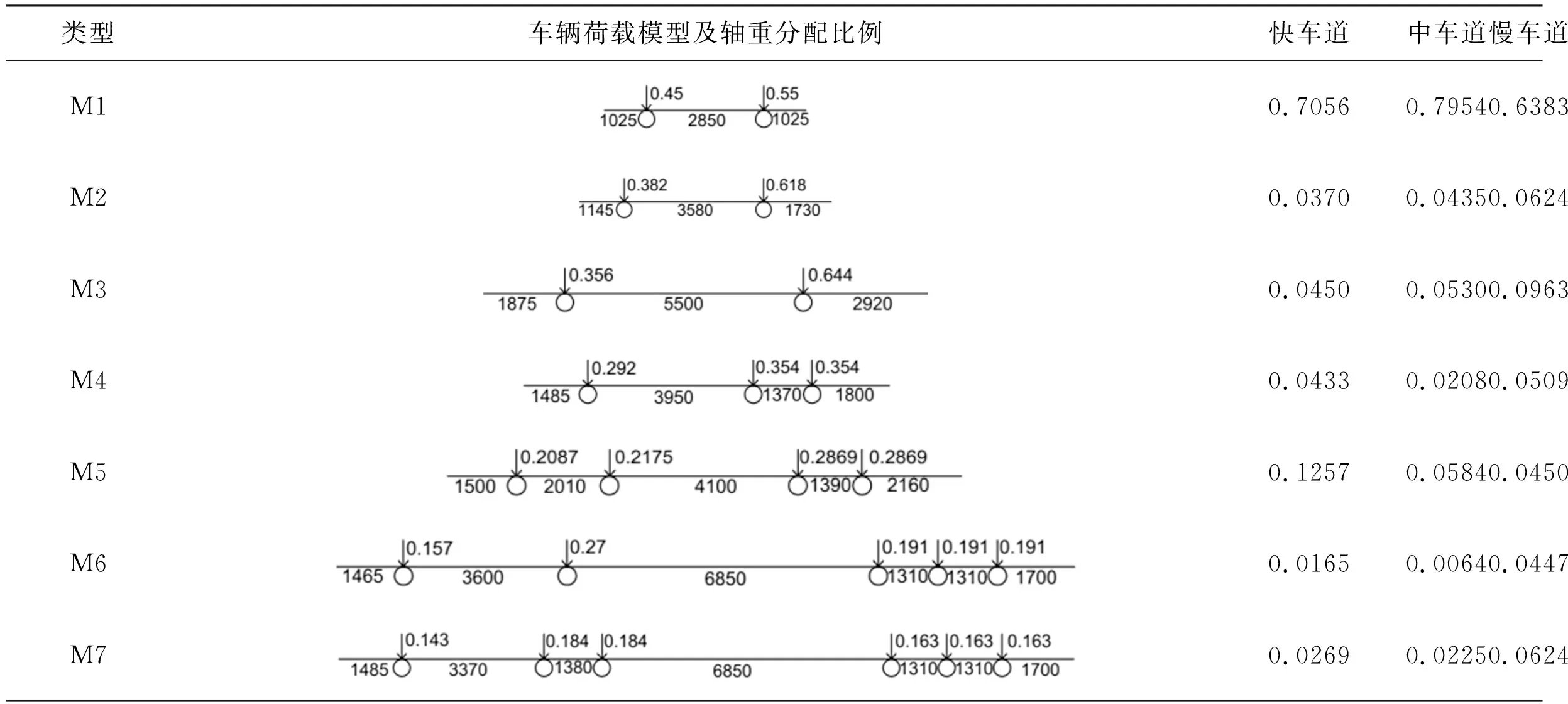
表1 车辆荷载模型及各车道车型比例(单位:mm)
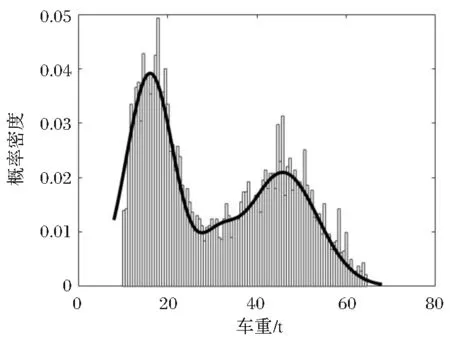
图1 M6车重分布拟合

图2 M7车重分布拟合
1.3 车间距分布
一定时间段内,通过该桥的车流量特别是大型货车流量极大,同时由于桥头平交路口的限制造成桥上经常性的车辆拥堵,因此,主要研究了密集和拥堵两种运行状态:在密集运行状态研究中,采用了文献[1]中提供的车辆间距概率密度函数,见式(1):

表2 各车型车重多峰正态分布参数(单位:t)
(1)
利用该函数,采用蒙特卡洛(M-C法)模拟的反函数法生成所需的车辆间距;对于拥堵运行状态的研究,取实际测量值平均值:2m。
1.4 蒙特卡洛模拟
运用Matlab软件编制荷载流加载程序,其大致流程为:输入车辆数量N,由车辆比例确定每类车型数量;利用M-C法由车间距、各车型车重分布类型随机生成车间距、各车型车重随机数;提出研究对象影响线数据,进行影响线加载运算,荷载每向前移动0.1m计算一次荷载效应值,将10次计算结果中最大值保存下来,作为车辆荷载效应样本数据。计算流程见图3:
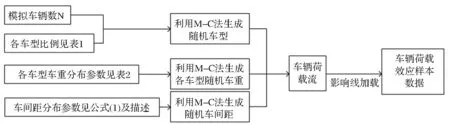
图3 车辆荷载效应计算流程图
2 POT理论
由于车辆荷载效应尾部数据对极值外推的影响甚大,故选取POT理论公式拟合荷载效应尾部数据。
2.1 理论简介
设X1,X2,…,Xn是来自同一分布F(x)的样本且随机变量X能满足下面的分布函数:
(2)
则称随机变量X服从广义帕累托分布[12-13](General Pareto Distribution,GPD),其中,u,ξ∈ R分别是位置函数和形状参数,σ > 0是尺度参数。
由GPD分布可知,当u足够大时,其高尾部分的条件分布可以用GPD模型来表示。随机变量X的低、中、高尾的分布函数F(x)的表达式为:
(3)
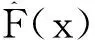
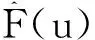
(4)
2.2 阈值的确定
阈值u的选取有图解法和计算法。图解法对阈值u的选取是判断阈值改变所引起参数估计量的变化或根据平均超出量函数的线性变化,但其存在较强的主观性。故选取计算法当中的峰度法[14],其大致流程为:
(1)计算样本数据峰度值Kn:
(5)
(2)对Kn进行判断,当Kn≥3,剔除|Xi- Xn|中最大值对应的Xi;
(3)重复以上两个步骤,直至Kn<3;
(4)选取保存下来的数据中最大值为u。
2.3 参数估计
矩估计法和极大似然估计法是参数估计的常用方法。经对比分析,对参数进行估计本文选取了极大似然估计法,其大致过程为:
(1)求出GPD分布对应密度函数的似然函数:
(6)
(2)对似然函数取对数并求偏导数,令其为0得:
(7)
3 车辆荷载效应的POT模型参数及外推
3.1 POT模型参数分析
基于调查分析数据和POT理论,得到不同运行状态下各跨径简支梁桥跨中弯矩的荷载效应值参数,见表3、表4。图4是密集运行状态下跨径为10m的简支梁桥荷载效应尾部数据的拟合情况,可见,利用POT理论对大于阈值u的车辆荷载效应值进行拟合有着良好的效果。
3.2 车辆荷载效应极值外推
由极值理论[7]可知,设计基准期T内车辆荷载效应最大值分布为:
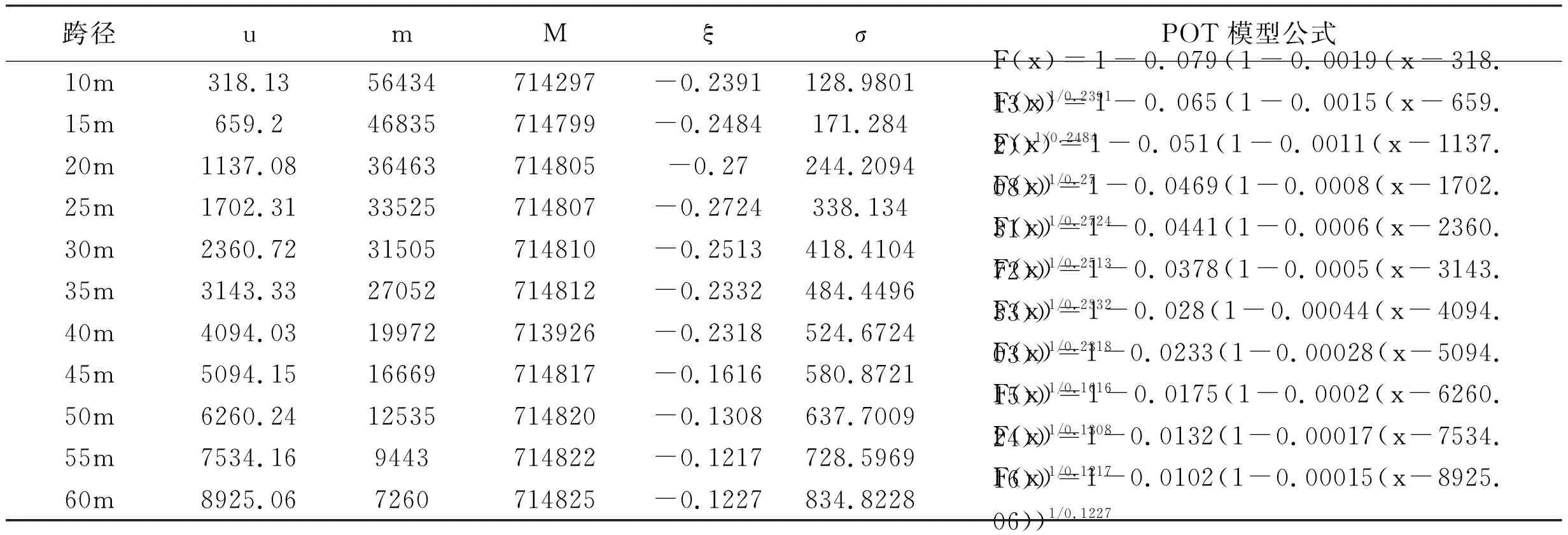
表3 密集运行状态各参数
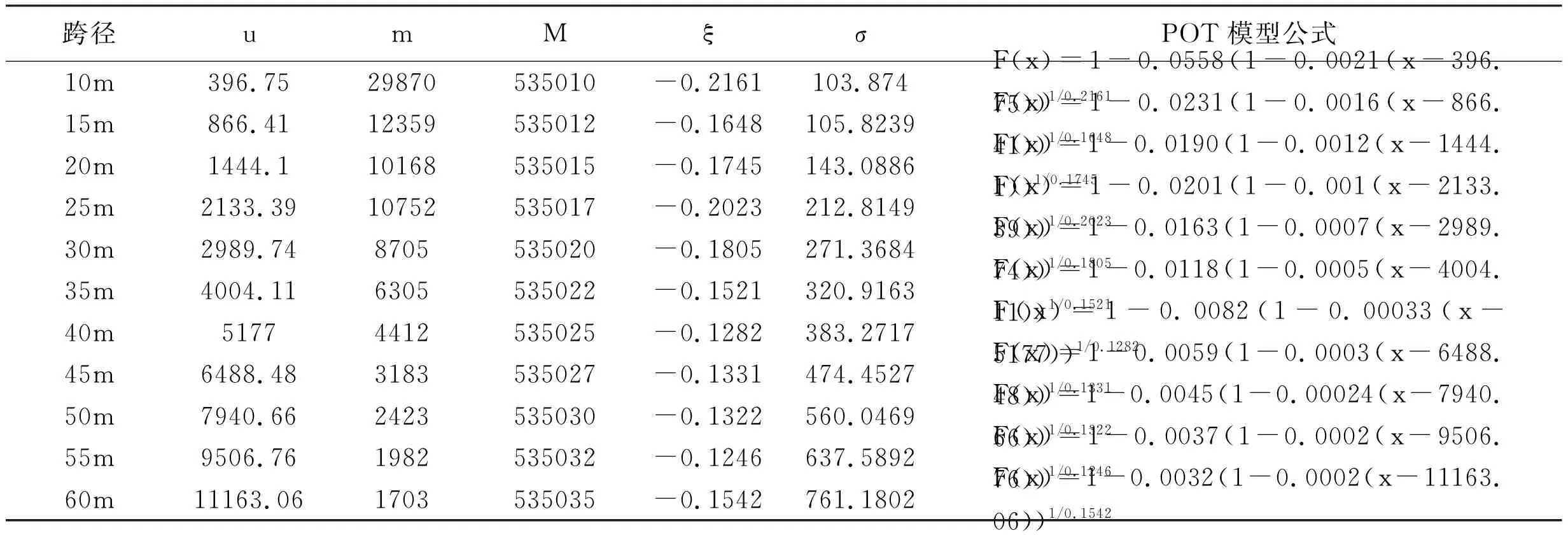
表4 拥堵运行状态各参数
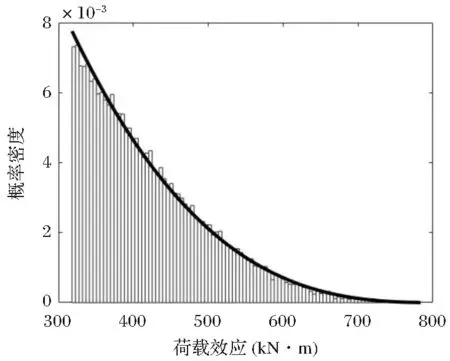
图4 10m简支梁荷载效应尾部数据拟合
FT(x)=[F(x)]N
(8)
对于桥梁工程中常取保证率为95%[15],可得[F(x)]N=0.95,其中,F(x)为车辆荷载效应样本数据分布函数,N为不同设计基准期对应的天数365×a,a为设计基准期对应的年份。
利用式(8)对POT理论得出的F(x)进行极值外推,得到不同设计基准期内车辆荷载效应极大值分布FT(x),并取0.95分位值作为效应标准值S,将S值与规范值S0相除即可得无量纲弯矩比K=S/S0。S0的取值为城市-A级中均布荷载qk和集中荷载pk共同决定的,其中,qk=10.5kN/m,pk值由桥梁计算跨径L0确定:当L0≤5m时,pk=180kN;5m
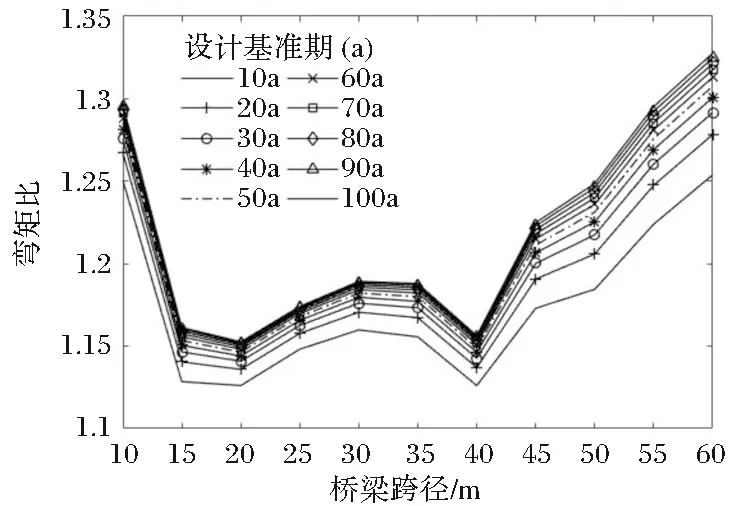
图5 密集运行状态下跨径-弯矩比关系图
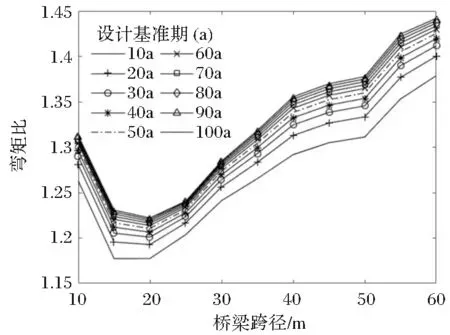
图6 拥堵运行状态跨径-弯矩比关系图
由分析可知,随着桥梁跨径的增加,两种运行状态的弯矩比都有着下降段和上升段,出现这种情况是因为实际荷载效应值的增长率比规范值增长率慢或快的原因造成的,但比值均大于1。而且,桥梁跨径的增加,不同设计基准期内弯矩比最大值和最小值之差也随着增大。总体而言,密集运行状态下不同设计基准期内外推值是规范值的1.13~1.38倍,拥堵运行状态下是规范值的1.18~1.46倍。
4 结论
(1)运用蒙特卡洛法模拟车辆荷载流并计算出不同运行状态下不同跨径简支梁桥的跨中弯矩值,利用POT理论对大于阈u的尾部数据进行处理,拟合效果良好,减少了因尾部数据拟合的误差对荷载效应外推值而产生的影响。
(2)不同设计基准期内,对各个跨径的荷载效应比值的分析可知,虽不同跨径有着不同的比值,但实际值都要比规范值大,即密集运行状态实际值是规范值1.13~1.38倍,拥堵运行状态下是规范值的1.18~1.46倍。可见,为了安全起见,一方面,在以后的桥梁设计中应适当地提高规范中均布荷载qk或集中荷载pk的取值;另一方面,政府应该加大治超政策的落实。
