基于机器学习的毫米波大规模MIMO混合预编码技术
2019-10-18刘斌任欢李立欣
刘斌 任欢 李立欣


【摘 要】毫米波大规模多输入多输出技术是提高5G移动通信容量的核心技术之一,其中混合预编码技术作为大规模MIMO系统中最关键的技术而被广泛研究。采用传统的迭代算法解决混合预编码问题通常导致较高的计算复杂度和严重的系统性能损失。机器学习方法由于其具有自适应学习和决策的优势而被应用于混合预编码器的设计工作中。在机器学习的基础理论上提出了一种采用交叉熵优化策略的混合预编码算法,通过迭代更新具有稳健误差的交叉熵损失函数得到最佳的混合预编码器组合,该组合被证明可以实现理想的传输总和速率,可以显著提高系统的能量效率。
【关键词】机器学习;交叉熵;混合预编码;大规模MIMO
doi:10.3969/j.issn.1006-1010.2019.08.002 中图分类号:TN929.5
文献标志码:A 文章编号:1006-1010(2019)08-0008-06
引用格式:刘斌,任欢,李立欣. 基于机器学习的毫米波大规模MIMO混合预编码技术[J]. 移动通信, 2019,43(8): 8-13.
Millimeter wave (mmWave) massive multi-input and multi-output (MIMO) is one of the key technologies to improve the capacity of 5G mobile communications, where hybrid precoding has been widely studied as the most critical problem in massive MIMO systems. The traditional iterative algorithms for hybrid precoding problems usually lead to high computational complexity and severe system performance loss. Machine learning is adopted in the design of hybrid precoders due to its advantages of adaptive learning and decision making. Based on the fundamental theory of machine learning, a hybrid precoding algorithm using cross-entropy optimization strategy is proposed. By iteratively updating the cross-entropy loss function with robust error, the optimal hybrid precoder combination is obtained. The combination has been shown to achieve an ideal transmission sum rate and significantly increase the energy efficiency of the system.
machine learning; cross-entropy; hybrid precoding; massive MIMO
1 引言
大规模多输入多输出(MIMO)通信技术将在第五代移动通信系统中得到广泛的应用,MIMO天线的数量可以是成千上百个,理论上可以实现无限的通信容量。与此同时,该技术的实现需要理想的低功耗射频组件,并要求所有的复杂处理运算在基站处进行,例如信道估计、预编码和权值计算等。具体而言,基站作为发射端通常包含预编码器,该编码器能够进行复杂的混合预编码,利用信道状态信息(Channel State Information, CSI)生成预编码矩阵,也就是对发射信号进行预处理操作。因此,高效而准确地建模并求解传统的混合预编码问题受到了业界的广泛关注。
机器学习作为自适应学习和决策的人工智能工具之一,已经在图像/音频处理、社会行为分析和项目管理等方面得到广泛应用[1]。近年来,机器学习与无线移动通信领域的结合不仅仅停留在理论的研究阶段,高速和强大计算能力的硬件技术的出现,使得机器学习理论已经成为现实。智能基站和移动终端可以模仿人类的复杂学习和决策能力,对耗时和计算密集的多样化问题迅速做出最优决策。通过对毫米波大规模MIMO系统中的混合预编码问题进行严格建模,可以采用机器学习的方法训练出最优的预编码矩阵。在机器学习领域中的交叉熵[2]方法被應用于解决组合优化问题,这启发了将其应用于毫米波大规模MIMO系统中的复杂混合预编码方法的研究。
交叉熵方法来源于Kulback-Leibler距离,最早是在1997年由Rubinstein在估计随机网络稀有事件概率的自适应方法最小化算法中提出的。交叉熵理论是一种测量两个随机向量之间信息差异的计算方法,本质上是一种基于数学统计的全局随机优化算法。到目前为止,交叉熵方法已经被成功应用于建模为组合优化的各种问题中,包括缓冲区分配、电信系统的排队模型、神经计算、控制和导航、DNA序列比对、信号处理、调度、车辆路线、项目管理和可靠性系统[3]等。
本文在机器学习的基础理论上提出了一种采用交叉熵优化策略的混合预编码算法,通过迭代更新具有稳健误差的交叉熵损失函数得到最佳的混合预编码器组合,可以实现理想的传输总和速率,显著提高系统的能量效率。
2 研究背景
2.1 混合预编码
模数混合预编码是一项目前为止用于毫米波大规模MIMO系统中最有前景的混合预编码技术,旨在设计出低维的数字预编码器和高维的模拟预编码器,从而实现高效节能的混合预编码。混合预编码技术通过在数字预编码部分使用少量的射频链,在模拟预编码部分设计低成本的模拟电路从而实现接近全数字预编码的最优系统性能。
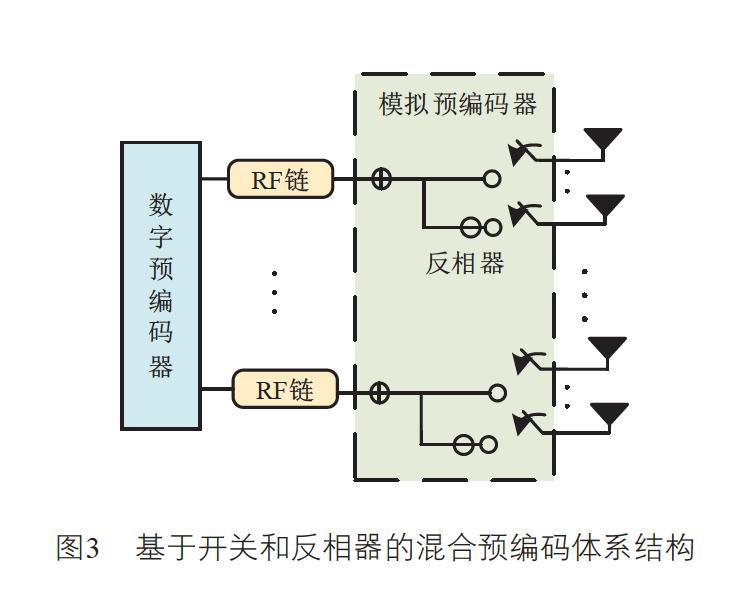
传统的混合预编码器中,模拟预编码部分可以使用移相器网络[6](如图1所示)或者开关选择网络[7](如图2所示),但是这两种方案分别在系统成本和性能上存在明显的缺陷。在大多数现有的文献中,移相器的能量消耗被证明是相对较高的(例如,4位移相器的能耗高达40 mW),而开关的能量消耗是很理想的(开关的能耗低至5 mW),但是图2所示的体系结构不能完全实现毫米波大规模MIMO阵列增益,导致了严重的系统性能损失。现如今,已有在无人机毫米波大规模MIMO场景中采用基于透镜阵列天线的混合预编码方案的研究[8],由此启发本文采用一种折中的混合预编码体系结构,模拟预编码部分由开关和反相器实现(图3所示)。事实证明,該体系结构的能量消耗远远低于移相器网络,同时,随着大规模MIMO中所有天线被使用,该体系结构还可以实现毫米波大规模MIMO阵列增益。
2.2 组合优化问题建模
交叉熵方法可以解决一般性的组合优化问题,其主要思想是通过构造随机序列,使其以一定的概率收敛到最优或次优的结果。设χ是一组有限的状态,S是χ上的实值性函数,实值函数S(x)的定义域为{x|x∈χ},若S(x)的最大值为γ*,则要使得下式取得最大值,本质在于寻找其对应的最佳状态,如公式(1)和(2)所示:
S(x*) γ*=S(x) (1)
其中,x*表示最佳的状态,在集合χ中寻找最佳的状态最大化实值函数S(x)。
首先,定义指示函数I{S(χi)}和参考概率密度函数族{f(.;v),v∈V},对于给定的实数γ,得到下面的关联估计表达式为:
其中,Pu是随机状态X 具有概率密度函数{f(.;v),v∈V}的概率度量,Eu表示相对应的期望算子,u 是某已知初始化概率分布的参数。如公式(2)所示,实值函数的最小化问题就转化为随机优化问题。
实际中应用交叉熵方法的应用主要有两个关键阶段:第一是根据一定的随机性或概率分布构造一个随机序列样本;第二是更新概率分布的参数,从而在下一轮迭代计算中产生更优的随机序列样本。
2.3 交叉熵方法
交叉熵量化信息量之间的“距离”——Kullback-leible距离[9],描述了两个概率分布之间的差异。当两个模型的概率分布保持一致时,交叉熵值更小,并且这两个模型之间的接近程度更大。更直观地讲,交叉熵的表达式为:
D(g,h)=Egln=∫g(x)lnh(x)-∫h(x)lng(x)
∫g(x)dx=1 (5)
∫h(x)dx=1 (6)
交叉熵方法解决了四个基本特征的问题:首先,根据优化目标建立概率密度函数,形成交叉熵目标函数;其次,根据概率分布函数生成样本集,并且参考目标函数的影响更新概率密度函数;然后,新概率分布函数用于生成一组新的样本,迭代重复目标函数;最后,当目标函数达到最优时,概率密度功能也达到了最佳解决方案。
交叉熵算法具有全局优化。它根据参数的概率分布密度函数生成样本解,在已经搭建好的组合优化问题模型中,概率分布和参数的形式决定了样本解决方案的整体质量。与其他智能算法相比,它避免了陷入局部最优和计算速度太慢的缺点。在优化过程中,交叉熵算法不要求每个生成的解决方案都优于样本解决方案的先前迭代的解决方案,但是在整个迭代过程中,预测结果往往越来越靠近理想中的标签样本。
3 基于机器学习的交叉熵混合预编码算法
3.1 混合预编码优化问题建模
本文采用如图3所示的基于开关和反相器的混合预编码架构,优化目标是设计出模拟波束形成器和数字预编码器的最优组合,使得系统可实现的总和速率达到最大,该优化问题可以表示为:
其中,表示满足由于图3的混合预编码体系结构带来的约束的所有模拟预编码器的集合,||FRFFBB||2F=ρ表示功率约束,η n 表示用户n 接收到的信干噪比。
在图3所示的体系结构中,每根射频链通过反相器和开关选择网络连接到天线子集,该连接方式导致模拟预编码矩阵成为块对角矩阵,如公式(8)所示。同时,由于反相器和开关被使用,模拟预编码矩阵中的元素取值有限,如公式(9)所示:
其中,表示第n个天线阵列上的模拟波束形成器。
第n个用户接受到的SINR可以表示为:
其中,hnFRF fBBnFHRFhHn表示用户n接收到的有用信号功率,hnFRF fBBiFHRFhHn表示用户n接收到的来自其他用户的干扰功率,σ2表示噪声功率。
因为公式(8)和(9)的存在,问题(7)成为一个模拟预编码矩阵FRF和数字预编码矩阵FBB的组合优化问题,本文要采用交叉熵方法得到最优的预编码矩阵组合,从而实现最大的系统总和速率。
3.2 具有稳健误差的交叉熵混合预编码算法
将交叉熵方法应用于上述组合优化问题,本文对传统的交叉熵方法加以改进,提出一种具有稳健误差的交叉熵混合预编码算法,与传统交叉熵方法类似,主要关注两个关键问题:第一:根据一定的随机性或概率分布构造一个随机序列样本;第二:更新概率分布的参数,从而在下一轮迭代计算中产生更优的随机序列样本。
本文所提出的具有稳健误差的高效节能混合预编码方案,步骤详细解释如下:
在算法具体实施之前,必要的准备工作有:将FRF中对角线的非零元素表示为N×1向量组,其中表示FRF矩阵中对角线的非零元素。FRF中元素的分布概率参数表示为N×1向量组u=[u1,u2,…,uN]T,其中un表示fn=的概率,fn是 f的第n个元素。
(1)对算法中的变量进行初始化,对于概率分布初始化u(0)=×1N×1,给迭代次数i赋初值i=0。
(2)基于概率模型(FRF;u(i))随机生成S个模拟波束形成器{FsRF}sS=1,其中概率模型即模拟预编码矩阵中元素的取值{-1,+1}的概率分布容易得到,该取值遵循伯努利概率分布。
(3)通过经典迫零数字预编码方法计算数字预编码矩阵{FsBB}sS=1,根据有效信道矩阵和模拟预编码矩阵之间的关系表达式Heq=HFRF,计算出有效信道矩阵Hseq,基带预处理之后的数字预编码矩阵可以表示为:
FsBB=(Hseq)H(Hseq(Hseq)H)-1 (11)
对数字预编码矩阵FBB的每一列进行功率归一化处理,即||FsRFFsBB||2F=1,确定生成最终的数字预编码矩阵FBB。
(4)计算经过迭代更新的预编码矩阵所实现的系统总和速率{R(FsRF)}Ss=1(由公式(7)和公式(10)计算可得),并且根据计算所得的总和速率对其排序R(F[1] RF)≥
R(F[2] RF)≥…≥R(F[s]RF)。
(5)计算FsRF的权重,通过公式(12)估计每个模拟预编码矩阵中元素的权重:
(6)更新FRF中元素的概率分布,也是交叉熵方法中最为关键的一步。
参考相对误差估计公式得到更新概率分布元素的公式(13):
最后,重复上述步骤,直到达到最大的迭代次数I,最终,模拟波束形成器FRF[1]将由接近最优概率分布的元素构成,从而得到数字预编码矩阵FBB[1]。
该程序中γ为可变参数,当γ>0时,γ为控制鲁棒程度的参数;当γ=0时,对应目标函数为负对数似然函数,并且随着γ增加,程序对于异常值的鲁棒程度增强。在实际中,可以通过基于γ-交叉熵的交叉验证来选择γ的值。该程序对异常值具有鲁棒性,该程序基于γ-交叉熵函数,已有仿真结果表明,该程序在预测精度方面比普通相对误差估计程序更加精确。
4 仿真结果
4.1 信道模型
本文采用几何信道模型获取毫米波MIMO信道的特征,信道矩阵如公式(22)所示:
4.2 仿真结果
这一部分提供了算法的仿真结果,如图4和图5所示。信道带宽设置为1 MHz;射频链的数量和数据流的数量是相等的,即NS=NRF=4;基站和射频链同时服务的单天线用户数为K=4;接收端的天线数目设置为N=64。信道矩阵中具体的参数设置如下:损失路径数目L=3,路径增益遵循标准正态分布αln~CN(0,1),方位角和到达角遵循均匀分布φnl ~U(0,2π)和θnl ~U(0,2π)(1≤l≤L)。实验设置参数如下:S=250,I=20。另外,在本文中,根據现有方法[10]的模拟结果,取γ值为0.5。
本文分别比较了全数字预编码方案、两阶段混合预编码方案、天线选择混合预编码方案以及本文所改进的具有稳健误差的混合预编码方案所能实现的系统总和速率和能量效率。
实验比较了不同算法所能实现的系统总和速率,结果如图4所示。在图4中,全数字预编码和两阶段预编码算法获得了良好的总和速率性能,天线选择预编码的总和速率性能最差,这是因为开关选择网络无法实现毫米波大规模MIMO系统潜在的阵列增益。而本文所提的具有稳健误差的交叉熵混合预编码可以达到远远高于天线选择预编码所能达到的系统总和速率。
另外,实验对比了系统的能耗随着用户数量(1~16)变化的性能,结果如图5所示。在图5中,随着用户数量的增加,两阶段混合预编码和本文所提的具有稳健误差的交叉熵混合预编码可以获得比其他两种预编码方案更高的能量效率。这是因为在前两种方案中低能耗的开关和其他少量耗能元件(反相器和移相器等)被使用,而在天线选择混合预编码中,仅由开关实现模拟预编码,导致系统的总和速率很低(如图4所示),从而无法实现理想的能量效率。而全数字预编码中复杂的移相器存在巨大的能量消耗,所以该方案下系统的能量效率是不理想的,在实际中,不建议采用此方案。
综合上述的实验结果,本文所提出的具有稳健误差的混合预编码算法可以取得预期的系统总和速率和理想的能量效率,验证了基于开关和反相器的混合预编码体系结构和本文所提算法的有效性。
5 结束语
本文提出了一种应用机器学习方法解决实际中毫米波大规模MIMO中的混合预编码器设计问题的方案,具体阐述了机器学习中交叉熵方法的应用原理和关键步骤,并将此方法应用于毫米波大规模MIMO场景中,解决可以构建为组合优化问题的混合预编码器设计问题,并通过实验解释验证了该方法的高效性和可行性。未来机器学习与无线通信结合的理论研究将是人工智能时代的重点,本文旨在为今后的研究工作提供思路和参考。
参考文献:
[1] M J Er, Y Zhou. Theory and Novel Applications of Machine Learning[M]. InTech, 2009.
[2] R Y Rubinstein, D P Kroese. The Cross-Entropy Method: A Unified Approach to Combinatorial Optimization, Monte-Carlo Simulation, and Machine Learning[J]. Technometrics, 2006,48(1): 147-148.
[3] X Huang, W Xu, G Xie, et al. Learning Oriented Cross-Entropy Approach to User Association in Load-Balanced HetNet[J]. IEEE Wireless Communications Letters, 2018,7(6): 1014-1017.
[4] G Alon, D P Kroese, T Raviv, et al. Application of the Cross-Entropy Method to the Buffer Allocation Problem in a Simulation-Based Environment[J]. Annals of Operations Research, 2005(1): 137-151.
[5] H Xie, F Gao, S Jin. An Overview of Low-Rank Channel Estimation for Massive MIMO Systems[J]. IEEE Access, 2016(4): 7313-7321.
[6] A Alkhateeb, Y H Nam, J Zhang, et al. Massive MIMO Combining with Switches[J]. IEEE Wireless Communications Letters, 2016,5(3): 232-235.
[7] J Gu, W L Liu, S J Jang, et al. Cross-Entropy Based Spectrum Sensing[C]//2010 IEEE International Conference on Communication Technology, 2010: 373-376.
[8] H Ren, L Li, W Xu, et al. Machine Learning-Based Hybrid Precoding with Robust Error for UAV mmWave Massive MIMO[C]//2019 IEEE International Conference on Communications (ICC). Shanghai, China, 2019: 1-6.
[9] S Buzzi, C D Andrea. Doubly Massive mmWave MIMO Systems: Using Very Large Antenna Arrays at Both Transmitter and Receiver[C]//2016 IEEE Global Communications Conference (GLOBECOM). 2016: 1-6.
[10] K Hirose, H Hirose. Robust Relative Error Estimation[J]. Entropy, 2018,20(9).★
