基于车辆动态响应的车轮多边形自动识别方法
2019-10-18徐晓迪刘金朝孙善超王卫东胡晓依
徐晓迪,刘金朝,孙善超,王卫东,胡晓依
(1.中国铁道科学研究院研究生部,北京 100081;2.中国铁道科学研究院集团有限公司基础设施检测研究所,北京 100081;3.中国铁道科学研究院集团有限公司铁道科学技术研究发展中心,北京 100081)
车轮磨损形式主要包括轮缘磨损、车轮擦伤、踏面沟槽磨损、踏面凹形磨损、车轮多边形磨损等[1]。车轮多边形磨损是铁路车轮沿踏面圆周方向的波浪形状磨损[2]。当列车高速运行时,车轮多边形会导致高频轮轨冲击,对车轴、车轮、钢轨等车辆-轨道系统零部件疲劳寿命产生极为不利的影响。为保障列车运行安全性和舒适性,对车轮多边形的研究有重要意义。车轮多边形变化的圆周曲线依次定义为1 阶(偏心)、2阶(椭圆)、3阶多边形以至18阶多边形,见图1。
国内外专家学者关于车轮失圆做了大量研究工作。文献[3-4]在北美东北走廊的高速线路上发现了车轮非圆化磨耗现象,并利用试验与数值仿真的方法进行了研究。文献[5-6]总结了车轮失圆的研究成果,并且对车轮失圆进行了分类,如扁疤、车轮多边形等。李奕璠等[7]提出了基于Hilbert-Huang变换的列车车轮失圆故障诊断方法,通过形态滤波-能量原则算法进行分析,结果表明:正常车轮与故障车轮间以及不同类型的故障车轮之间Hilbert 谱差异显著。陈博等[8]提出了基于改进EEMD(Ensemble Empirical Mode Decomposition)和遗传算法支持向量机的诊断方法,用于识别车轮多边形故障。

图1 不同阶次车轮多边形磨耗示意
高阶车轮多边形磨耗对应高激励频率,更容易激发起高能量的系统共振[9]。在带有局部故障的车辆动态响应信号中,平稳成分与故障成分会出现在同一时间内,但是分布在不同的频段内。车辆动态响应信号中的平稳成分一般分布在低频中,而包含轮轨系统故障信息的瞬时成分一般分布在高频中。高频共振解调技术是根据实际情况选择某一固有振动频率作为研究对象,通过中心频率等于该固有频率的带通滤波器将信号的固有振动分量分离出来,从而清楚地看出隐含的故障信息。文献[10]和文献[11]分别利用自适应共振解调方法和基于STFT(Short-time Fourier Transform,短时傅里叶变换)的振动信号解调方法对轴承故障进行了诊断。本文借鉴以上2种思想,提出了基于同步压缩STFT的自适应共振解调方法,并利用该方法分析车辆动态响应数据,对高速列车多边形磨耗进行了诊断。
1 基于同步压缩STFT的广义共振解调方法
以车辆动态响应数据作为试验对象,研究基于同步压缩STFT的广义共振解调方法,诊断车轮多边形的有效性和实用性。高速列车运行速度在200~350 km/h,当车轮出现多边形时,轮轨系统容易出现高频激振,同时在相应的频带内会出现等间隔谐波成分。在故障发生时,有时这些谐波成分会因工况的变换隐藏于其他成分中,通过共振解调可以挖掘出其频率间隔Δf与车辆运行速度和车轮周长的对应关系。
基于同步压缩STFT的广义共振解调方法的步骤如下:
1)利用同步压缩STFT对车辆动态响应信号进行时频变换得到其时频谱,变换中的窗长通过集中性度量准则来确定;
2)利用Lp范数准则选取解调频带;
3)利用广义Hilbert包络解调分析得出解调信号的幅值谱。
基于广义共振解调的车轮多边形磨耗在线自动识别过程见图2。
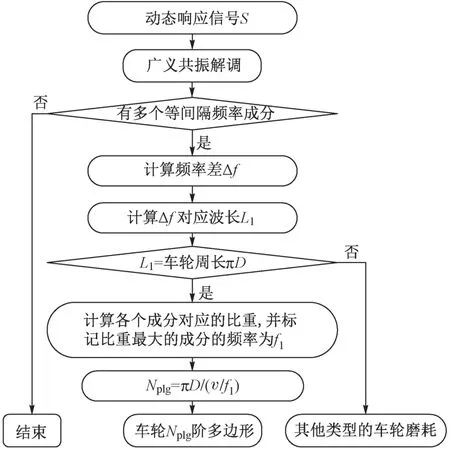
图2 车轮多边形磨耗在线自动识别过程
1.1 同步压缩STFT
假设f为具有下列形式的K个AM-FM成分的叠加:
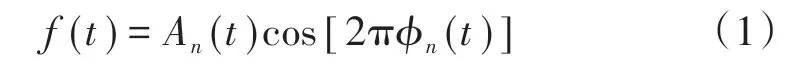
式中,φn(t)的导数
基于同步压缩STFT的瞬时频率提取步骤如下:
1)对于信号f(t)和固定的窗函数g,进行STFT变换:

2)计算信号的瞬时频率,表达式为

3)根据计算得到的瞬时频率,对通过STFT计算得到的时频平面进行时频重排,亦即同步压缩。其过程可以表示为
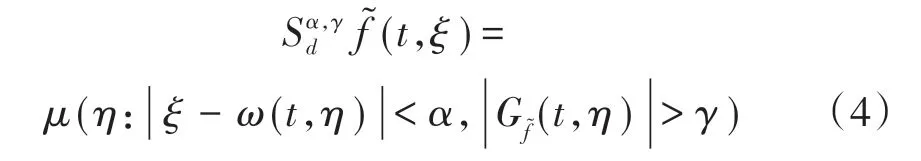
式中:d为两个连续分离成分的下界;阈值γ≥0;(t,ξ)∈R×αN;分辨率α>0;μ为R上的Lebesgue测度。
有效的集中度量CM可以刻画信号的不同分布特性,信号的集中性越好含有的成分就越单一,因此,采用信号在时频谱上的最大集中度量来决定最佳变换窗长是合理的。记ξi所处频带的集中度量[8]为

式中:
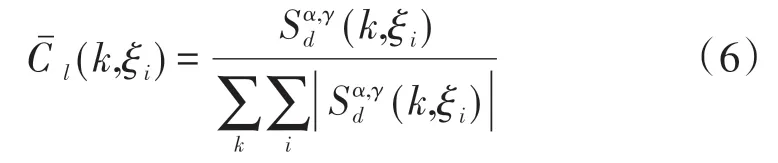
定义ξi所处频带的最佳窗长
根据以上法则即可确定变换的最佳窗长,从而清晰地看出信号中隐藏的故障特征。
1.2 Lp范数准则
对车辆动态响应信号解调分析的目的是将车辆动态响应数据中的周期性故障信号提取出来,但是没有必要将所有的被调制成分完全解调出来。所以需要利用一种合适的准则,将最佳滤波频带选取出来,同时这个选定的频带要包含最丰富的被调制信号的信息,然后利用该选定的频段解调出的信号进行幅值谱分析。本文中选取的准则为Lp范数准则[10]。
对于车辆动态响应数据S(k),k=1,2,…,N/2,N为采样点数,对它进行同步压缩STFT,得到的时频谱为S(k,ωj),k=1,2,…,N;j=0,2,…,N/2。定义时频能量谱为
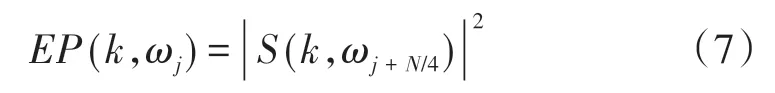
基于式(7),利用Lp范数准则可以得到车辆动态响应数据S(k)的时间-能量信号为
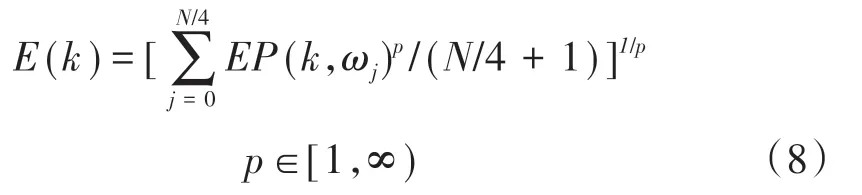
式(8)中增加常数项是为了避免当采样点数发生变化时对时间-能量信号进行频谱分析的结果会改变。当p→∞时,式(8)可以写成

显然,式(8)和式(9)量纲一致。
1.3 广义Hilbert包络解调分析
在实际运用中,包络谱与车轮多边形磨耗的理论特征缺陷频率有较明确的对应关系,但是只需要将被调制信号中含有的周期性成分解调出来即可,并不需要完全恢复被调制信号。所以本文选择利用广义Hilbert包络解调方法进行分析[11]。
假设调制信号为
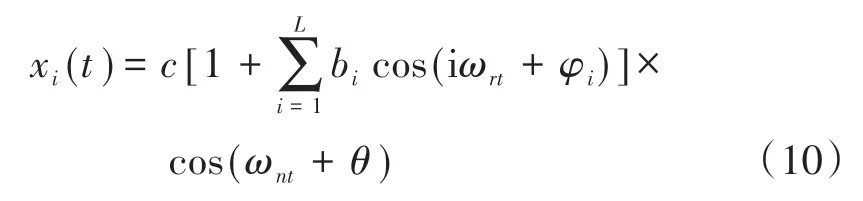
对上述信号进行复解析带通滤波,假设通带包含频率成分ωn+kωr+iωr,k∈[-L,L],i=1,2,…,n。令ωi=ωn+kωr+iωrk,那么处理后的信号可以表示为
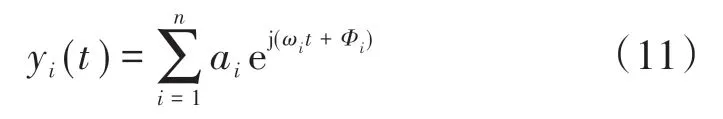
对照Hilbert包络解调方法,对式(11)取模以后进行Taylor级数展开并取一次项,可得

因为

所以,解调出的信号成分包含ωr,2ωr,…,(n-1)ωr等频率。
即使车辆动态响应信号的带通滤波器的中心频率与调制信号的载波频率不同时,也可以解调出被调制信号中的周期成分。但由于该方法并非严格意义上的Hilbert包络解调,不能完全恢复被调制信号[11]。
2 应用实例
利用广义共振解调方法对车辆动态响应数据进行分析,轴箱加速度信号见图3,其功率谱和同步压缩STFT之后的时频见图4。可见,故障频率主要集中在550~660 Hz。
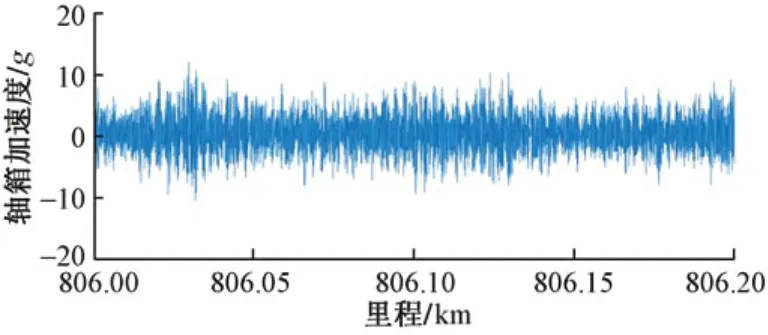
图3 轴箱加速度

图4 功率谱和时频
通过本文提出的方法共振解调以后,信号的包络谱见图5(a)。用传统方法对数据进行共振解调计算,结果见图5(b)。
对比图5(a)和5(b)可知,传统共振解调方法经过试选滤波频带最终计算结果与本文提出的方法计算结果相近,但是并没有更加完全地将各成分解调出来,在70 Hz 和100 Hz 附近的能量不明显。而利用本文所提出的方法,可以清晰地看出车辆动态响应故障频率及其倍频成分。其峰值间隔恰好等于车轮多边形磨耗响应周期,即

式中:D为车轮直径;v为行车速度。
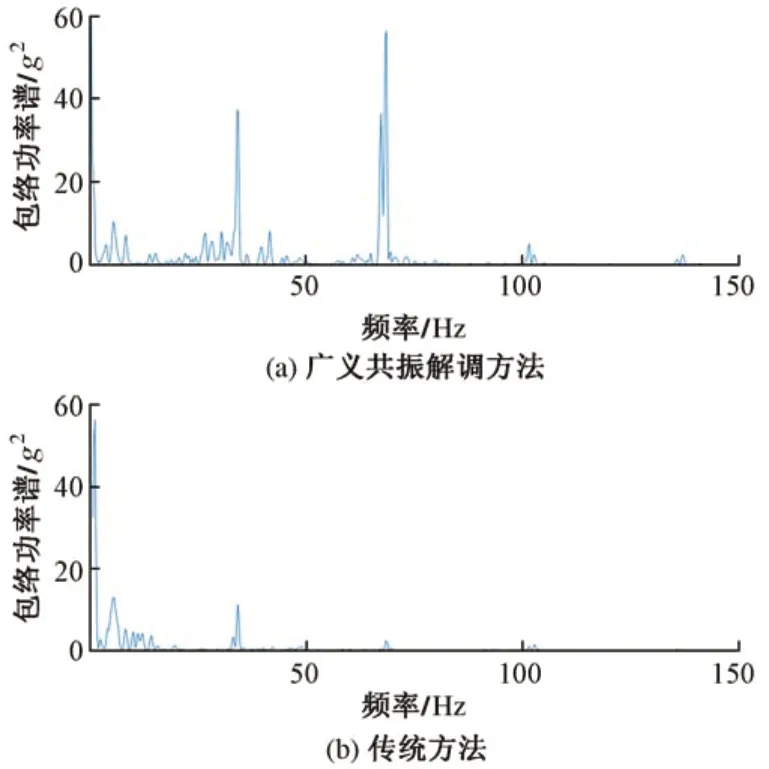
图5 包络谱
通过数据的功率谱和时频图可知,所分析的车辆动态响应数据的主频为548 Hz。通过计算可知该数据对应车轮存在高阶多边形,多边形阶数为16 阶。
通过对轮对的测试,可知该车轮的确存在16阶多边形,车轮表面磨耗数据见图6。图6(b)中的数值表示与标准车轮半径的差。由图6(c)可见,粗糙度水平已经超过了10 dB/μm。
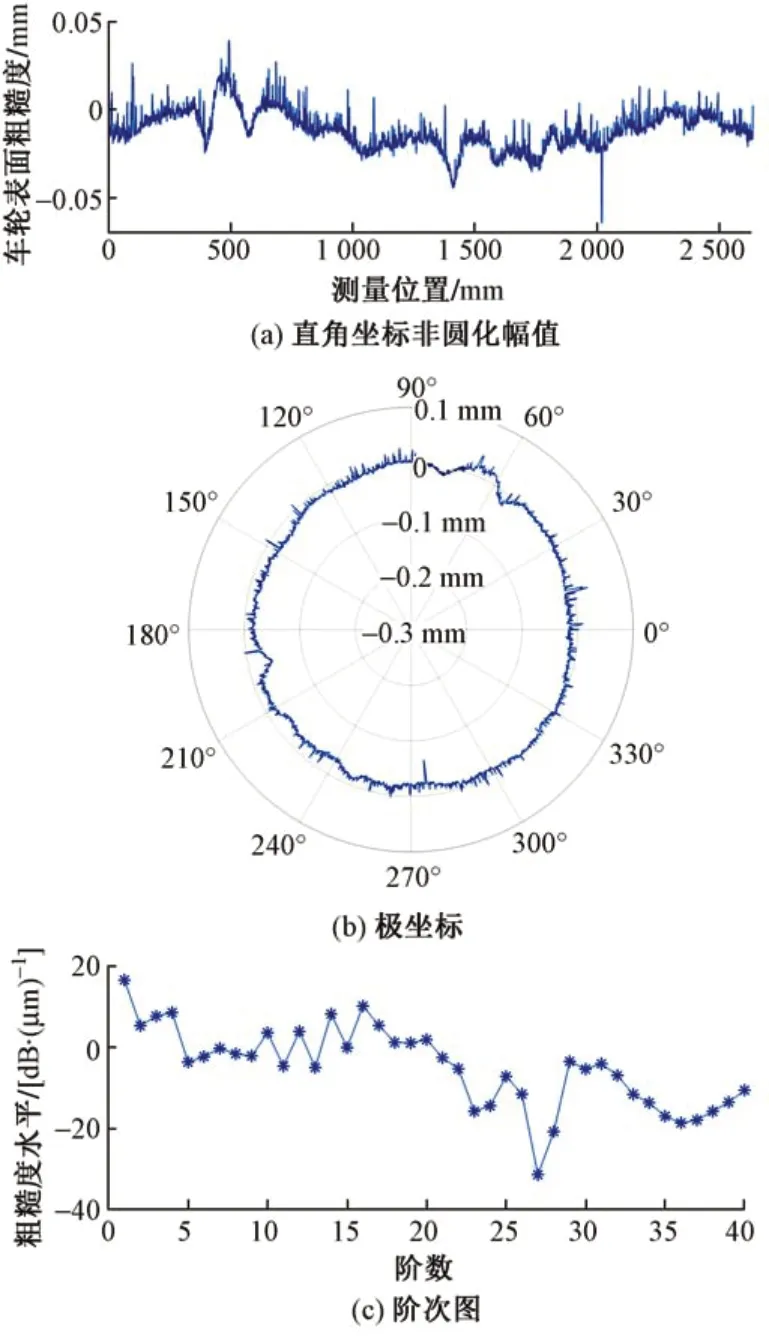
图6 车轮表面磨耗数据
3 结论
1)利用基于同步压缩STFT 的广义共振解调方法对高速列车车轮多边形进行了诊断,并提出了自动识别方法。数值计算结果表明,该方法可以有效地诊断车轮多边形。
2)文中所使用的广义共振解调方法通过对时间振动信号的时频分析,基于时间-能量准则选取车辆动态响应数据的带通滤波范围,可以更准确地将含有丰富故障信息的频带分离出来,避免了传统方式在带通滤波时中心频率和带宽难以确定的困难。
3)基于车辆动态响应的车轮多边形自动识别方法,通过对车辆动态响应数据进行分析,能够实时检测高速列车车轮状况,及时发现车轮多边形磨耗。
