大跨度高速铁路桥梁模态参数频域识别方法研究与应用
2019-10-18魏剑峰
魏剑峰
(中国铁路设计集团有限公司,天津 300142)
桥梁的动力性能直接影响高速铁路列车的运行安全和乘客舒适度。模态参数是频率、振型和阻尼比的统称,是评价桥梁结构动力特性的重要指标。目前常用的模态参数识别方法分为时域分析法、频域分析法和时频分析法。其中频域分析法包括峰值拾取法和频域分解法,在工程中得到了广泛应用。
对结构动力问题研究的本质是对输入、系统和输出之间的相互关系进行分析。模态参数的识别属于控制工程的系统识别,即利用系统的输入(激励)和输出(响应)对参数进行识别[1],在结构动力学中称为第1类逆问题[2]。大跨度桥梁中采用的环境激励,无法准确获取系统的输入,只能使用响应数据进行模态参数识别,这种方法称为工作模态分析(OMA,Operational Modal Analysis)方法[3]。
本文采用峰值拾取法和频域分解法对实桥进行模态参数识别,并与有限元计算结果进行对比,以评价2种识别方法的精度和可靠性。
1 桥梁模态参数频域识别方法原理
本文采用基于OMA环境激励的频域方法对大跨度高速铁路桥梁进行模态参数识别。在工程中常用的模态参数频域识别方法是峰值拾取法(Peak-Pick)和频域分解法(Frequency Domain Decomposition)。
1.1 频率识别
1.1.1 峰值拾取法
峰值拾取法[4]的原理是利用频响函数在特征频率处产生峰值的特性,从频响函数中的峰值位置直接选取特征频率。
桥梁结构系统的频响函数[2,5]为
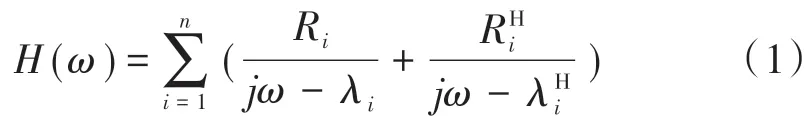
式中:λi为极点,包含了各阶特征频率的信息;Ri为函数在极点的留数;上标H为矩阵的复共轭转置;i为模态阶数;ω为模态频率。
由于OMA环境激励方法属于只有响应的测试方法,无法得到系统的输入信号。因此采用功率谱密度函数来替代频响函数。
峰值拾取法识别模态参数的基本流程:①获得在环境激励下结构响应信号;②利用获得的原始数据计算结构振动的功率谱密度函数;③用功率谱密度函数代替桥梁结构的频响函数,对桥梁的模态参数进行识别。
1.1.2 频域分解法
频域分解法是一种采用白噪声激励在频域内进行模态参数识别的方法[6]。其原理与峰值拾取法类似,不同之处在于频域分解法引入了奇异值分解技术[7],即通过对桥梁结构系统的功率谱密度矩阵进行奇异值分解(SVD,Singular Value Decomposition),用奇异值曲线代替相应的频响函数。
频域分解法假定采用白噪声激励,系统响应的功率谱密度矩阵为
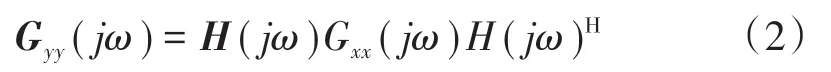
式中:Gyy(jω)为系统功率谱密度矩阵;H(jω)为结构频响函数矩阵;Gxx(jω)为输入的功率谱密度矩阵,其对角线元素为监测结构各自由度响应的自功率谱,非对角线元素为结构不同自由度响应的互功率谱[8]。
频域分解法识别模态参数的基本流程:①获得结构的M个测点的响应信号xi(t),i=1,2,3,…,M,其中t为测试时间;②计算结构响应的功率谱密度矩阵Gyy(jω);③在不同频率下对功率谱矩阵进行奇异值分解,进而识别结构的模态参数。
1.2 阻尼比识别
采用半功率带宽法[9]的原理是通过频响函数(功率谱密度函数)的峰值识别结构的特征频率。在峰值附近搜索峰值倍的2个点,称为半功率点。阻尼比为

式中:f1和f2为2个半功率点对应的频率值;fr为峰值位置的频率。
1.3 振型识别
功率谱密度矩阵经过奇异值分解后,可以得到3个矩阵,即
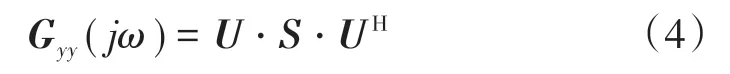
式中:U,S,UH均为经过奇异值分解后的矩阵;U矩阵对应的第1列向量即为识别的某阶振型。
2 工程概况
石济客运专线济南黄河公铁两用桥,跨度为(128+3×180+128)m,结构形式为刚性悬索加劲钢桁梁的特殊结构。主桁及桥面板钢材均采用Q370。钢桁梁采用3 片主桁,其中心间距为14.65 m,桁高15 m,桁式为有竖杆的三角形桁式。桥面系采用纵横梁体系的正交异性桥面板整体桥面。下层桥面为铁路桥面,一侧为设计速度250 km/h 的客运专线,采用ZK 活载设计;另一侧为客货共线的联络线,采用中—活载设计。上层桥面为公路桥面,为双向六车道,采用公路一级荷载设计。通过采用MIDAS/Civil 2017 建立有限元模型进行模态分析,桥面板采用板单元模拟,吊杆采用桁架单元模拟,其余均采用梁单元模拟。桥面板和主桁、横梁之间采用刚性连接。全桥共建立节点28 904 个,梁单元 22 673 个,桁架单元 96 个,板单元12 896个,模型见图1。
测试传感器采用941B 型振动传感器,共8 台竖向振动传感器。测试时微型拨动开关置于1 档加速度档,通频带范围为0.25~80.00 Hz。采集仪采用美国NI生产的模拟信号采集仪。采样频率为100 Hz,单次采样时间为10 min,得到桥梁在环境激励下的加速度时程曲线,见图2,计算得到相应的功率谱密度函数,见图3。

图1 桥梁结构有限元模型
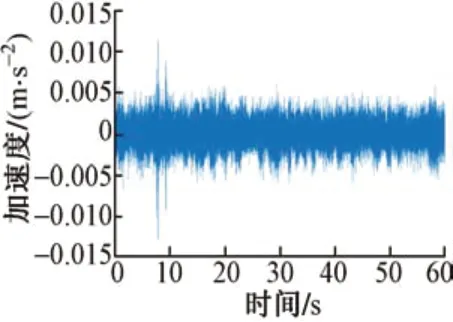
图2 加速度时程曲线
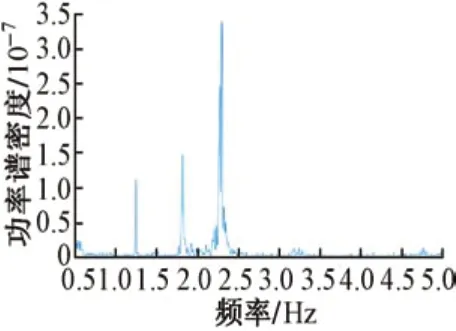
图3 功率谱密度函数
3 识别结果及分析
3.1 频率识别结果
对测试数据分别采用峰值拾取法和频域分解法得到前4 阶频率,并与有限元计算结果进行对比,见表1和表2。可知:峰值拾取法和频域分解法1阶识别频率与有限元计算结果偏差极小,最小偏差仅为0.05%;随着模态阶数的增加,识别频率与计算频率的相对偏差有逐渐增大的趋势,最大偏差为3.28%。误差主要由信号处理过程中的频率泄露[10]产生。上述结果表明频率识别结果真实可信,满足工程中的精度要求。
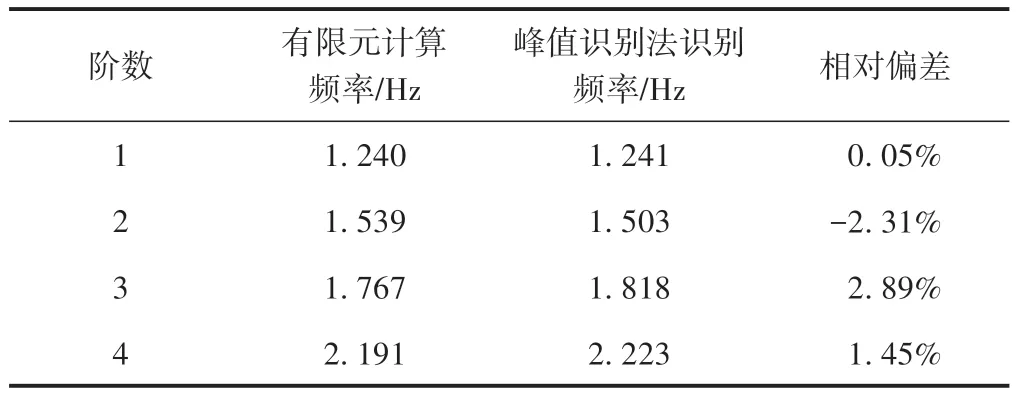
表1 峰值拾取法频率识别结果
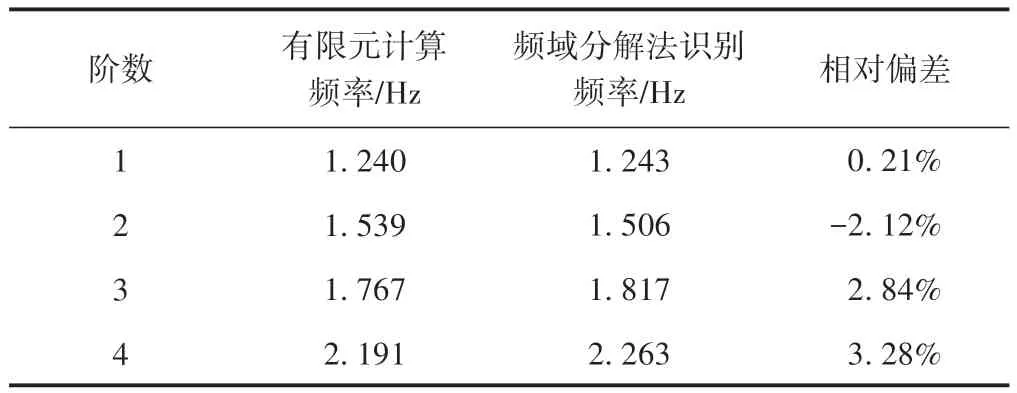
表2 频域分解法频率识别结果
3.2 振型识别结果
全桥共布置8 个加速度传感器,提取前2 阶的有限元计算振型,见图4。图中标出了传感器位置。采用频域分解法对第1 阶和第2 阶振型进行识别,并对计算振型和识别振型进行归一化处理,见图5。可知,识别振型结果与计算振型结果基本吻合。
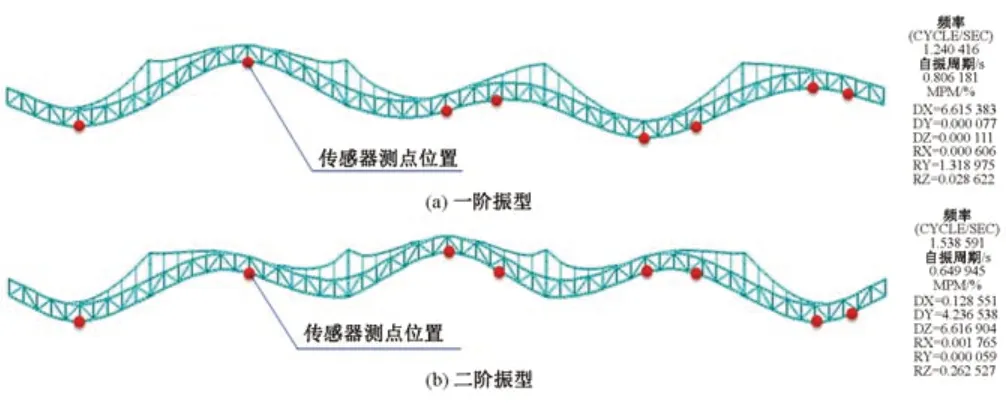
图4 桥梁有限元模型振型
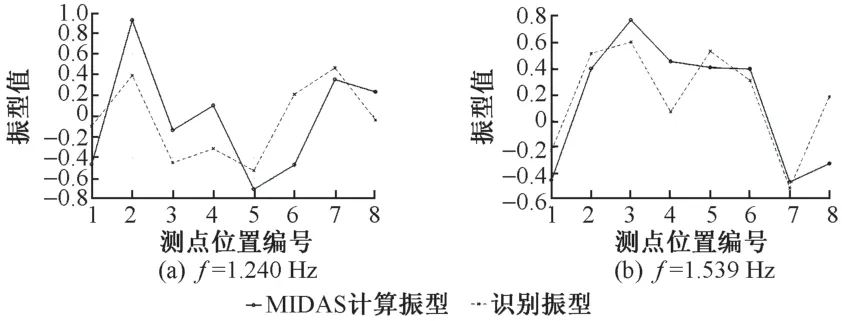
图5 计算振型与识别振型对比结果
振型识别过程中发现振型识别结果的精度与测点数量关系较为密切,测点数量越多,振型识别精度越高。定义振型因子α,用于评价振型的识别精度。随着α的增大,振型精度随之降低。其计算式为

式中:L为桥梁总长;N为传感器数量。
3.3 阻尼比识别结果
采用半功率带宽法对相应阶数的阻尼比进行识别,得到4阶阻尼比,结果见表3。可知,识别阻尼比在0.018 1~0.029 8。GB 50011—2010《建筑抗震设计规范》[11]中规定钢结构的阻尼比一般取值在0.02~0.04,说明阻尼比识别结果可信。

表3 阻尼比识别结果
4 结论
1)功率谱分析过程中需要采用加窗的方式对信号进行截断,在此过程中产生了由频率泄露导致的误差。实际工程应用时,识别模态参数精度可以满足工程需要且操作简单,具有较强的抗噪性。
2)模态频率的识别结果与传感器布设位置有关,部分测点在某阶频率下振动微弱,导致测试信号强度不够,无法识别某阶频率。因此,测点应尽量布设在振动较为明显的位置。
3)频域分解法的抗干扰能力较强,采用奇异值分解的方法可以有效分离噪声,在噪声污染较为严重的环境中进行模态参数识别具有独特的优势。信号采集部分有必要增加抗混叠滤波器,防止高频干扰导致的频谱混叠,提高频谱精度。
4)振型识别精度与测点数量关系较为密切。对于大跨度桥梁,根据经济性和振型识别精度的要求,应选择合适的测点数量。
5)由于实测阻尼比识别结果均为离散数据,部分模态识别频率无法恰好落在离散频率点上,需要进行插值处理,这样会降低阻尼比的识别精度。因此,适当提高频率分辨率可以提高阻尼比的识别精度。
