用“运动的合成与分解”分析复杂运动

徐富清

(扬州市邗江区公道中学 江苏 扬州 225119)

不久前，讲授“万有引力”一章时学生提出一个问题：月球绕太阳运动的轨迹为什么是一个摆线？为什么不是圆形或其他图形？怎样分析月球的运动？带着这个疑问笔者上网查询了一些资料，发现有很多典型的运动，如果使用“运动的合成与分解”的思想分析，它们的运动过程、运动轨迹就很好理解，并且可以回避复杂的数学运算，而且随着参数的变化，结果也不尽相同.由于要揭示复杂运动背后的规律，笔者将借助MATLAB这款软件，将复杂运动以图形、可视化方式表现出来，本文主要对下面3个典型的案例进行分析.

1 月球绕太阳的运动

(1)简化运动模型

以太阳为中心建立x,y轴，太阳处于圆心O，地球绕太阳运动的半径为R，其运动轨迹称为本轮，月球环绕地球运动的半径为r，月球绕地球运动的轨迹称为均轮，如图1所示.

图1 简化的运动模型

(2)建立函数

假设地球绕太阳运动的角速度是ω1，月球围绕地球运动的角速度为ω2，则地球绕太阳运动的圆周运动方程为

月球绕地球运动的圆周运动方程为

根据运动的合成与分解，可将两个分运动x方向、y方向分别相叠加，就得到月球绕太阳运动的圆周运动方程

(3)使用MATLAB描绘运动轨迹

为了突出反映该模型背后的变化规律，我们取

同时改变R和r的值，下面使用MATLAB工具描绘出运动轨迹.

1)若R=20,r=3，结果如图2所示，月球运动轨迹显示的是一个闭合的摆线.

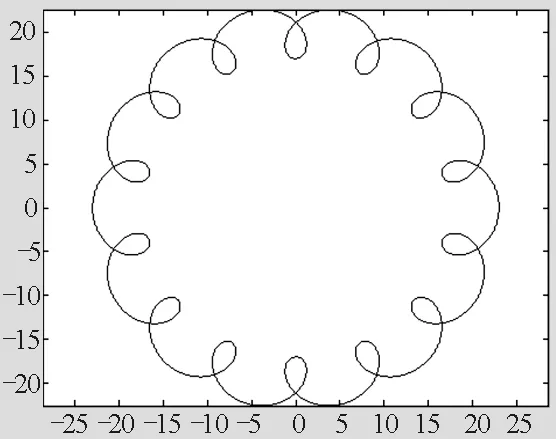
图2 R=20,r=3时,月球的运动轨迹

2)若R=20,r=11，其运动轨迹如图3所示，随着月球轨道半径r的增加，摆线渐渐地发生重叠，且中心部分形成一个多边形.

图3 R=20,r=11时,月球的运动轨迹

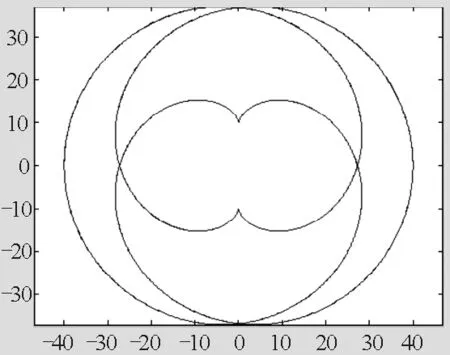
3)若R=20,r=20，即月球绕地球运动的半径与地球绕太阳运动的半径相等(不考虑太阳对月球的影响)，月球的运动轨迹如图4所示，此时月球要经过太阳点，中心部分形成一个花瓣状.

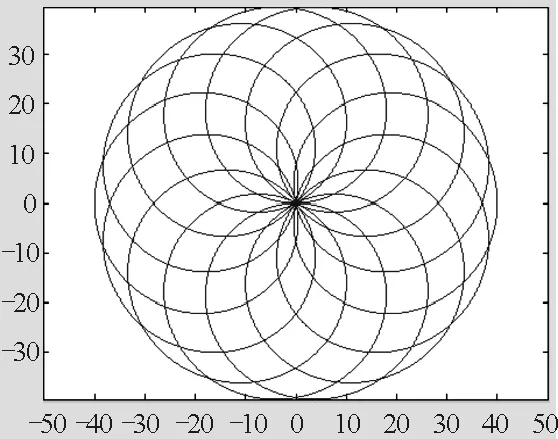
图4 R=20,r=20时,月球的运动轨迹

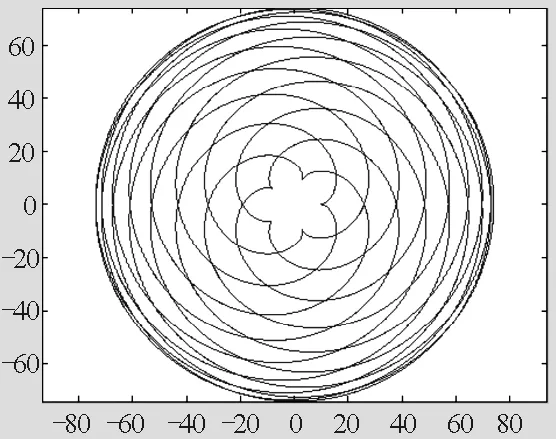
4)若R=20,r=30，即月球绕地球运动的半径超过地球绕太阳运动的半径，月球运动轨迹如图5所示，其中心部分趋近于一个圆形.

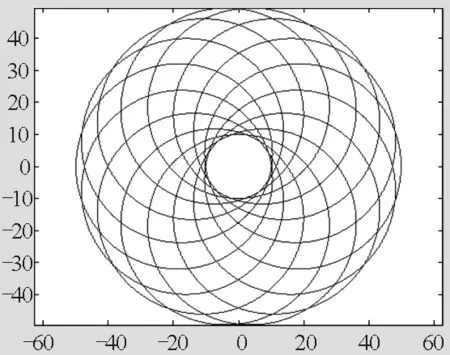
图5 R=20,r=30时,月球的运动轨迹

2 小齿轮围绕大齿轮的运动

(1)建立模型

假设大齿轮静止不动，半径为R，小齿轮绕大齿轮作无滑滚动，半径为r，如图6 所示.

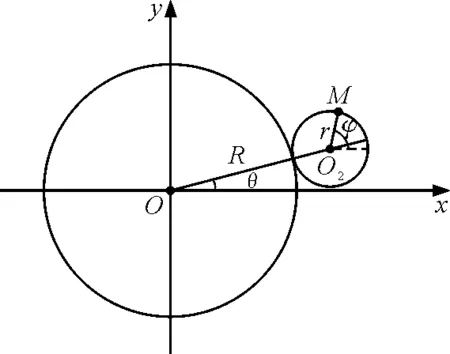
图6 小齿轮围绕大齿轮运动的简化模型

(2)建立函数

假设起始时圆心O、接触点、M点共线，当小齿轮在大齿轮上滚过角θ时，小齿轮上的M点转过角φ，则小齿轮的圆心O2围绕大齿轮O的圆周运动方程为

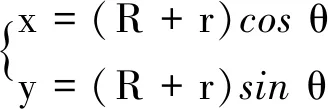
M点围绕小齿轮O2的圆周运动方程为

同理根据运动的合成与分解，将两个分运动分别在x,y轴相叠加后，M点围绕大齿轮O的圆周运动方程为

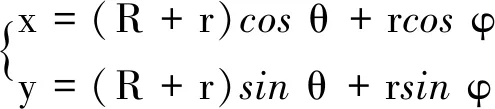
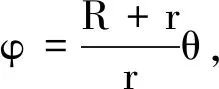
(3)使用MATLAB描绘运动轨迹

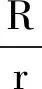
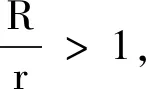
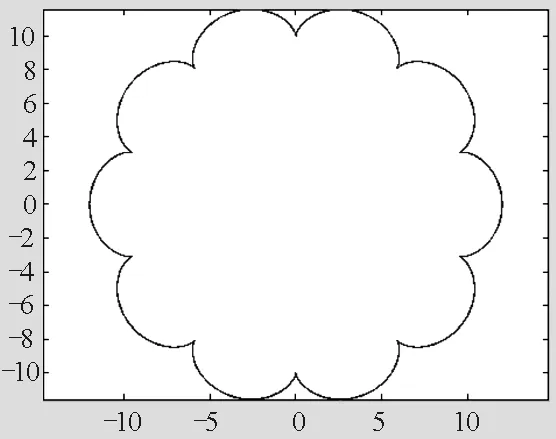
图点的运动轨迹

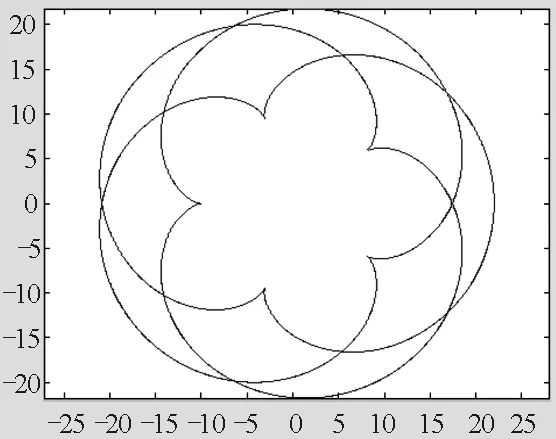
图点的运动轨迹

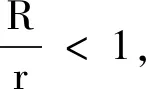
图点的运动轨迹

图点的运动轨迹

3 汽车的轮缘运动

(1)建立模型

设汽车车轮半径是r，汽车匀速直线运动的速度是v，车轮匀速转动的角速度是ω，且车轮作无滑滚动，满足方程v=rω，如图11 所示.

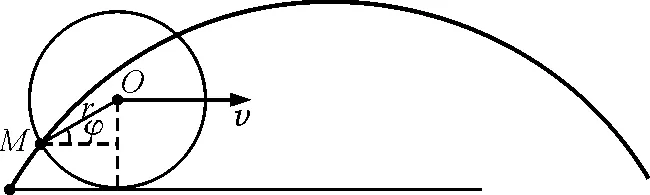
图11 汽车轮缘运动的简化模型

(2)建立函数

轮缘M点的运动可以看作是两个分运动的叠加，一是随圆心O在水平方向上的匀速直线运动，即x=vt，二是M点围绕圆心的匀速圆周运动

同理根据运动的合成与分解，将两个分运动叠加后，得到M点的运动方程

(3)使用MATLAB描绘运动轨迹

假设v=24 m/s,ω=30 rad/s时，车轮的临界半径为

使用MATLAB工具作出运动轨迹.

1)当车轮的半径r=0.8 m，则M点的运动轨迹如图12所示，其形是一个直线花边.

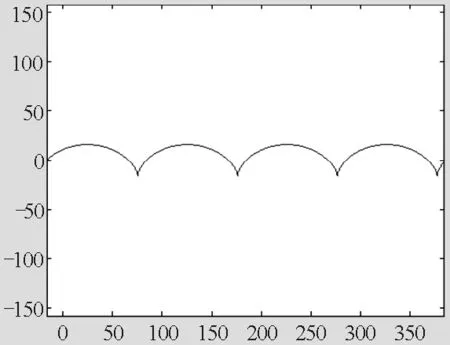
图12 r=0.8 m时，M点的运动轨迹

2)若取车轮内的点P作为研究对象，即r<0.8 m(如图13所示)，则P点的运动轨迹如图14所示，其形似一个波浪.

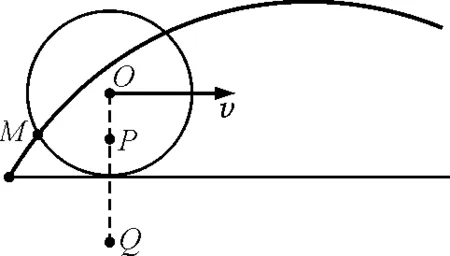
图13 取P点为研究对象

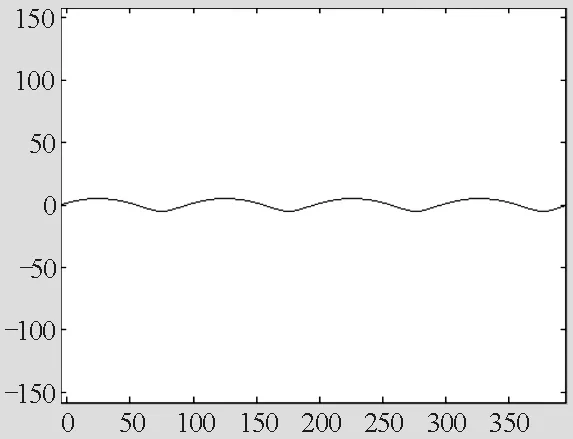
图14 r<0.8 m时，P点的运动轨迹

3)若取车轮外的点Q作为研究对象，即r>0.8 m(如图13所示)，则Q点的运动轨迹如图15所示，结果呈现为摆线形状.

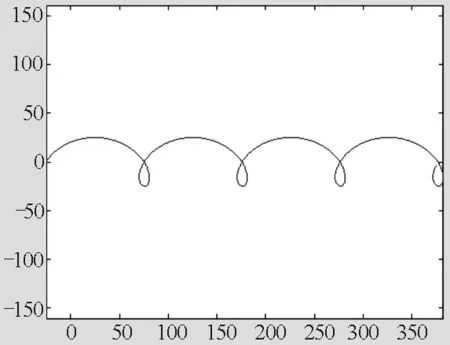
图15 r>0.8 m时，Q点的运动轨迹

4 结束语

当笔者将所发现的结果向学生一一展示，学生学习的好奇心高涨，这不仅仅是结论也包括探究的过程.这就给我们一个启发，那就是对于一个看似简单的事物如果进行细致的研究和分析，往往会带来意想不到的惊喜.物理教学的目的是培养学生的科学素养、激发他们的想象，知道物理课程不是单调枯燥的，其关键是教师以何种方式激发学生的兴趣，并把这种力量带到学习中去.