以模型建构为核心培养学生的科学思维能力——以“法拉第圆盘发电机”为例

余潘

(浙江省慈溪中学 浙江 宁波 315300)

法拉第圆盘发电机是人类历史上第一台发电机[1]，揭开了机械能转化为电能的序幕，把人类带向了电气化时代.在教学过程中引导学生经历类似科学家探究物理的过程，感知科学发现的魅力，增强对科学的理解，提升科学素养[2].但在具体教学实施中发现学生对法拉第圆盘发电机的理解不清晰、不透彻，并从“磁通量未改变”的角度对产生感应电流提出质疑.本文根据学生的困惑，从不同角度对法拉第圆盘发电机模型进行剖析，试图突破难点，揭示本质.

1 复杂物理模型的等效分解

为了帮助学生理解复制模型，在教学过程中设置合理的梯度，引导学生将法拉第圆盘发电机模型按图1进行等效分解处理.

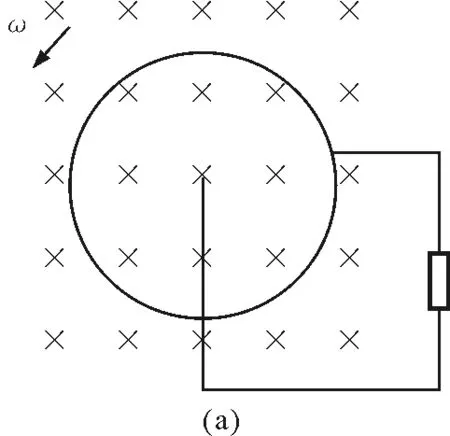
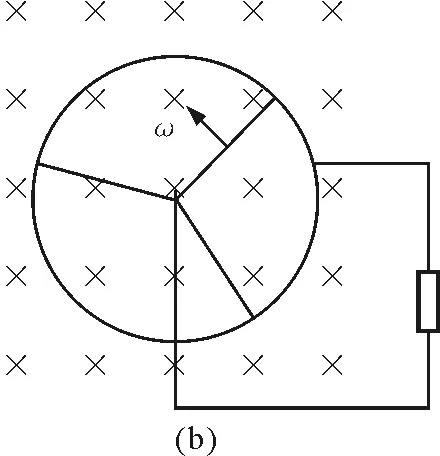
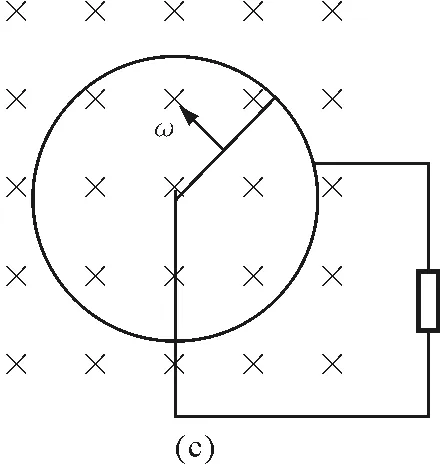
图1 法拉第圆盘发电机模型等效分解图

在推理思路上，以逆向递进(d)(c)(b)(a)顺序更容易被学生接受，符合认知规律.即从最简单基本的单导体棒平行切割模型图1(d)，通过微元法过渡到单导体棒旋转切割模型图1(c)，再类比多导体棒旋转切割模型图1(b)，相当于电源的并联，再结论推理到无数根导体棒旋转切割模型即法拉第圆盘发电机模型图1(a).学生很容易意识到法拉第圆盘发电机模型产生的感应电动势与单导体棒或多导体棒旋转切割模型产生的感应电动势相等，感应电流方向可由右手定则判断，为半径方向.法拉第圆盘发电机内阻，相比单导体棒或多导体棒旋转切割，在获得相同的电动势情况下，圆盘发电机的内阻更小，输出效率更高.

2 从磁通量变化角度解释

从磁通量角度分析，关键是研究回路的选取，已有文献对此进行了等效电路的研究[3,4]，但其等效模型复杂，学生理解困难.本文以图1(d)最简单基本的模型将单导体棒与圆盘进行类比等效，如图2所示.

图2 单导体棒与圆盘进行类比等效

若将电刷放在间距Δr较小的圆环上，由于间距小，可以认为内环与外环长度相等，此时将圆环展开，等效成如图3所示.

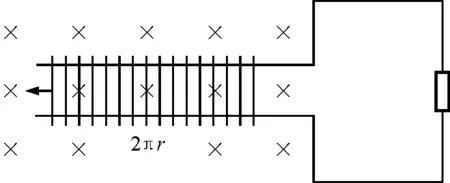
图3 将圆环展开

相当于在长度为2πr的矩形区域内，有无数根长度为Δr的导体棒源源不断的以速度v=rω向左平行切割.以任一根导体与电阻所构成的回路为研究对象如图4所示.

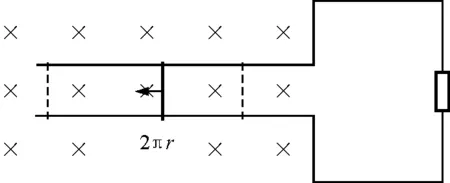
图4 导体棒与电阻所构成的回路

回归到最简单基本的单导体棒切割模型，即可从磁通量变化角度来解释.此导体棒即为电源，电动势ΔE=BΔrrω，无数根导体棒同时切割作为电源并联关系，不改变电动势，只减小内阻，与前者讨论结果一致.若将电刷间距增大，不改变定性结果，便于学生理解，不做定量计算.

3 从感应电动势本质角度解释

从微观角度分析，感应电动势的本质是自由电荷在非静电力作用下的定向移动，如图5所示.

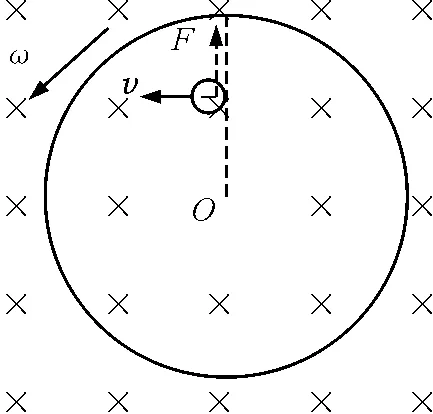
图5 自由电荷在洛伦兹力作用下定向移动

由于圆盘转动，圆盘上的自由电子由于受到沿半径方向的洛伦兹力而定向移动形成电流，方向为半径方向，与前者讨论结果一致.便于学生理解，此处只讨论了洛伦兹力的一个分力(充当非静电力)，而对洛伦兹力的另一分力及自由电荷由于径向运动产生的科里奥利力不做讨论.

4 结束语

在教学实践中发现，通过复杂物理模型的等效分解与科学推理，有效帮助了学生对法拉第圆盘发电机的深入理解.通过该案例，引导学生积极自主进行模型建构、科学推理来解决生活学习中遇到的问题与困惑，从而达到培养学生科学思维素养的目的[5].