基于原始物理问题的初中物理教学初探

鲁植全

(云南大学附属中学 云南 昆明 650031)

1 引言

在平时的教学中，很多次遇到这种现象：给学生一个计算题学生会做了，再给学生一个可以用同样方法来测量出某个物理量的实验设计题学生就不会了，而且无从下手.由此引发了笔者的困惑和思考：明明解决问题的方法类似，为什么学生表现出的差异却如此之大呢？后来查阅资料了解到：物理问题可以分为“原始物理问题”和经过抽象后而理想化的“物理模型问题”，即常见的物理习题两大类.所谓“原始物理问题”是指未经过人为抽象化和理想化加工的、来自自然现象和生活生产技术的实际物理问题.北京大学物理系赵凯华教授曾经指出：在我们的教学中，同一物理问题，既可以把原始物理问题提交给学生，也可以由教师把物理问题分解或抽象成一定的数学模型后提交给学生，而我国的学生往往获得的是后者而非有血有肉的物理现象，缺少了将原始问题转化成抽象问题的过程培养，所以在遇到原始问题时往往会不知所措.

目前很多教师都在关注这一问题，都在反思学生出现这种现象是否是我们教师所造成的，是否是应试教育所造成的必然结果？很多教师呼吁进行深层次的教育改革，要求我们不能再惟考施教，应着眼于学生的能力发展，走出课堂，联系社会.因此，在教学中适时穿插一些物理原始问题对切实提高学生解决实际问题的能力显得尤为重要.在初中密度的知识学习完之后，笔者选择了密度的测量作为教学内容，将物理原始问题融入课堂教学做了一次尝试.

2 教学案例

上课一开始，笔者直接问学生们：小明在家里发现了一瓶液体，不知道是什么液体，你能帮他想办法判断出液体的种类吗？

当笔者把问题给出之后，有不少学生表情诧异而又一脸茫然，然而很快就有学生举手要发表自己的看法.

生：可以测量液体的密度，因为密度可以用来鉴别物质.

学生们纷纷点头表示赞同.

师：那么，怎么测出该液体的密度呢？

师：怎么用天平来测量液体的质量呢？实验步骤有哪些？

生：液体不能直接倒入天平托盘，所以我们应该使用一个量筒，先测出空量筒的质量；再将液体装入量筒中，天平测出量筒和液体的总质量；二者相减得到液体的质量.

这个方案一提出来，就立即有学生举手起来说道：刚才的这种方案有个错误，量筒要放置在水平桌面上，而天平在使用过程中横梁会左右摇摆，所以量筒不能放在天平上.我认为应该把量筒换成烧杯，测量步骤为，先测出空烧杯的质量m1；再将液体装入烧杯中，天平测出烧杯和液体的总质量m2；二者相减得到液体的质量.再将液体倒入量筒测得体积V，从而代入密度公式计算液体密度

师：非常好.请大家对该测量方案进行评估，指出方案的不足.

生：我觉得刚才的方案会带来较大的测量误差，因为将液体从烧杯倒入量筒时倒不干净.

师：那你认为测量的密度偏大，还是偏小呢？

学生们沉思片刻后，纷纷举手.

生：因为是从烧杯倒入量筒时倒不干净，所以会导致后面所测得的液体体积偏小，根据密度公式可知测得的密度偏大.

师：那么怎么测量可以使得测得的液体密度更准确呢？

生：我打算先测量空烧杯的质量，接着在量筒中倒入要测量的液体，测出液体的体积；最后把量筒中的液体倒入烧杯中，测出液体和烧杯的总质量，减去空烧杯的质量就是液体的质量，带入密度公式可得到液体的密度.

该生刚一说完，就已经有好多个同学举起了手，纷纷要发表自己的看法.

生：这种方案还是存在从量筒里倒入烧杯中倒不干净的问题.

学生们纷纷表示赞同地点点头.

师：那么这种方案会使测得的液体密度偏大，还是偏小呢？

生：因为从量筒中倒入烧杯中倒不干净，会导致最后一步测得的液体质量偏小，所以密度偏小.

师：那么怎么使得测得的液体密度更准确呢？

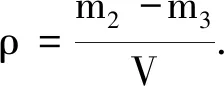
该学生说完后，班上立即就有好多学生露出了会心的微笑，也有一些学生情不自禁地为同学鼓掌喝彩.

笔者发现还是有部分学生对刚才的这种方案没有完全理解，于是就又重复分析了一遍，力争让每一位学生都理解方案怎么做到让质量与体积之间相互对应，从而减小误差的.

此时，又有学生举起了手，起来说道：我还有另一种方案，先测出烧杯和液体的总质量m1，接着只将部分液体倒入量筒中测出体积V，然后将装有剩余液体的烧杯一起测出总质量m2，这样原有总质量减去最后剩余的液体和烧杯质量就是倒入量筒中的液体的质量m1-m2，除以量筒中液体的体积就得到液体的密度

学生们纷纷鼓掌表示赞同，与前一个方案异曲同工.

在学生学完压强、浮力、机械等部分力学知识之后，笔者再次把这个密度测量的原始问题提出来.

师：如果测量工具只有弹簧测力计，你能否测出液体的密度？

学生听到这个问题更是一脸茫然.经过分组讨论之后，有小组汇报：可以利用浮力测出液体密度.首先找一个石块，用弹簧测力计测出其重力G；再将石块吊在弹簧测力计下浸没在水中，读出测力计的示数F1；再将石块吊在弹簧测力计下浸没在待测液体中，读出测力计的示数F2；根据物体浸没在水中时的浮力公式变形求出物体的体积

再利用物体浸没在待测液体中的浮力公式变形得到液体的密度为

师：如果测量工具只有刻度尺，你能否测出液体密度？

经过分组讨论之后，有学生汇报说可以利用自制密度计借助浮力知识测出液体密度：找一根粗细均匀的木筷，用金属丝缠绕在一端制成一个密度计，测出木筷的总长度L；将其放入水中使其竖直漂浮，测出筷子露出水面的长度L1；再将其放入待测液体中使其竖直漂浮，测出筷子露出液面的长度L2.假设木筷的横截面积为S，因为木筷漂浮时浮力等于重力，即

ρ水gS(L-L1)=ρ液gS(L-L2)

即可求解得到液体密度

又有小组学生举手说道：可以利用液体压强知识测量.找一根粗细均匀两端开口的玻璃管，将玻璃管的一端扎上橡皮膜，将玻璃管缓慢插入装有水的烧杯中,用刻度尺测出橡皮膜在水中的深度记为h1；往玻璃管内缓慢灌入待测液体，直至橡皮膜刚好变平，测出所倒入液体的高度h2；利用橡皮膜变平时水的压强和液体压强相等，列出等式

ρ水gh1=ρ液gh2

即可求解得到液体密度

3 教学案例分析

(1)原始物理问题能切实落实从生活走进物理、从物理走向社会的新课程基本理念

在教学中当笔者把第一个问题提给学生的时候，有不少学生是很茫然的：什么已知条件都没有，这样的问题要怎么去解答呢？这恰恰是我们在实际生活中常遇到的生活情境，在这样的情境下不可能还有已知条件，需要哪些条件，需要准备哪些工具等这些问题都需要学生自己去思考.而这种思考不是漫无目的的，是需要学生能够对所学习过的物理知识进行联系思考，并整合物理规律之间的联系.所以，这样的问题正好能够很好地体现新课程“从生活走向物理、从物理走向社会”的基本理念.

(2)原始物理问题有利于激发学生的学习兴趣

正因为原始物理问题源于生活，虽然学生一开始不知道从何处着手，但是学生却保有积极的解决问题的热情.

在本节课教学过程中，问题提出之后，学生展开了积极的讨论，提出了自己的测量方案，虽然有些学生的方案不完善，甚至有些学生的方案是错误的，但是学生在这种参与讨论的思维碰撞过程中能够不断进益，从而让问题在争论与讨论中越来越明晰，能够体会到参与学习的乐趣，学习兴趣也能够得到不断巩固.

(3)原始物理问题有利于提升学生分析解决问题的能力

原始物理问题由于其条件的隐蔽性，需要学生自己去寻找或创造已知条件，同时利用抽象思维从具体问题中构建出物理模型，这个将原始问题抽象为习题的过程能够很好地训练和发展学生构建物理模型的科学思维.

本节课对如何鉴定是什么液体，学生首先要将原始问题转化为物理问题：测密度.同时，在讨论中要理清天平的使用规则，量筒不能放在天平上等使用要求，误差分析方法，利用浮力、压强知识测量密度更需要学生有很强的综合分析问题的能力，所以，可以切实提高学生分析解决问题的能力.

本节课教学过程中对于只有刻度尺一个测量工具来测液体密度这一问题，有部分学生提出了利用自制密度计和利用两端开口的玻璃管来测密度，是非常好的办法，但是如果学生不是具备了很强的综合分析浮力、压强等问题的能力是几乎不可能做到的.虽然大部分学生直接想出这种方案是很困难的，但是在一起分析其他学生想出来的方案的过程中，对综合分析浮力、压强、密度等知识的能力也会有很大的提高.

此外，由于很多原始物理问题存在开放性、综合性、复杂性等特征，在学生无法单独解决问题时，往往需要配合使用讨论式教学方法帮助学生克服困难，这个过程除了可以很好地训练学生综合运用物理知识解决问题的能力之外，还可以很好地培养学生的交流与合作能力.

(4)原始物理问题有利于学生创新能力的发展，有利于学生科学素养的形成，为学生的终身学习和发展奠定基础

开放的原始物理问题，由于问题指向性不特定，所以学生可以从不同的角度入手，拓展学生的思维空间，有利于学生发散思维的形成和质疑创新思维能力的发展.

本节课中当如何鉴定是什么液体的问题提出来之后，有些学生从密度的定义公式出发，提出了天平和量筒测密度的方案，还有一部分学生提到了用弹簧测力计测重力的方案来测密度，还有部分学生提出了利用浮力知识测密度，还有部分学生提出了利用液体压强测密度，还有部分学生提出了利用杠杆测密度.

这种多角度的发散思维，能够促使学生理清物理规律之间的联系，有利于形成相互之间讨论、争论的学习氛围，帮助学生逐步形成质疑创新思维.这种从具体问题中构建物理模型、从物体间相互作用和联系的角度看问题、质疑创新等正是学生科学素养的重要形成过程.