基于费马点的网络连通性修复策略

周赵斌，章红艳，汪晓丁

基于费马点的网络连通性修复策略

周赵斌1,2，章红艳3，汪晓丁1,2

（1. 福建师范大学数学与信息学院，福建 福州 350117；2. 福建省网络安全与密码技术重点实验室，福建 福州 350117；3. 福建师范大学协和学院，福建 福州 350117）

网络有效性；连通性修复；三角剖分；费马点

1 引言

2 国内外研究现状

现有的1-连通性修复策略主要可分为两类。其中，一部分策略[1-11]利用构造SMT-MSP所消耗的资源(中继节点)与理论上最优SMT-MSP所需资源(中继节点)的比(即近似比)作为衡量标准，近似比越小算法的性能越好，而另一部分策略[12-14]则采用仿真实验来验证算法性能。

Chen等[11]提出基于四边形构造的近似算法，不仅证明此算法近似比为3，并且证明了单纯采用斯坦纳化最小生成树（MST）的方法来修复连通性的近似比也为3。在此基础上，Cheng等[8]提出基于三角形构造结合斯坦纳化MST的近似算法，以及基于3-超图最小生成树的随机近似算法，并证明这两者的近似比分别为3和2.5。尽管后者近似比较低，但其算法复杂度偏高。Lloyd等[9]提出一种改进的斯坦纳化MST法，近似比在6~7之间。Tang等[10]将部署区域划分成网络并对网络分簇，对于每个网格部署一个节点作为簇头负责簇内与簇间通信，从而恢复网络的1-连通性，此算法的近似比为4.5。Efrat等[3]、Yang等[6]、Misra等[5,7]对于节点与节点、节点与中继、中继与中继这3种不同连接方式给予相应的权值并以此构造赋权完全图，然后根据网络不同的应用场景，结合目前最优的最小权斯坦纳树构造算法[15]，提出近似比分别为3.11、6.43、6.2和12.4的修复算法。在文献[4]中，Wang等提出了一种结合Voronoi图和重心的算法。近期，Wang等[1]、Lalouani等[2]先后提出在网络中存在障碍物情况下基于直骨架的修复算法。

文献[12-14]通过仿真实验验证算法性能。Ranga等[13]提出一个基于0梯度点的修复算法。此算法首先利用连通分支构造一个凸壳，然后构造凸壳内各点与连通分支之间的距离函数并计算出能够使该函数梯度为0的点，最后以这个点为中心部署中继节点来连接各个分支。Joshi等[12]利用网络的直骨架并结合节点的传输半径，规划出一条最优的中继节点部署路线。陈洪生等[14]给出了一个基于四边形的连通度修复算法并证明了其时间和信息复杂度。

表1 各算法在近似比和复杂度方面的对比

3 预备知识

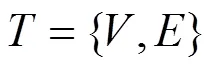
4 系统模型

针对此问题，本文提出了一种高效的连通性修复策略（RSFP，restoration strategy based on fermat point）。

5 RSFP策略

该策略通过7个步骤来实现网络1-连通性的修复，具体执行步骤如下。

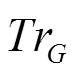
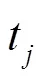
以下将给出一个RSFP修复网络连通性的例子。

图1 一个RSFP示例

6 理论分析

本节对策略RSFP在近似比与复杂度方面进行分析。

证明

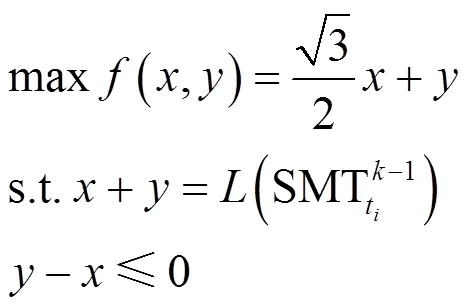
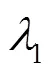
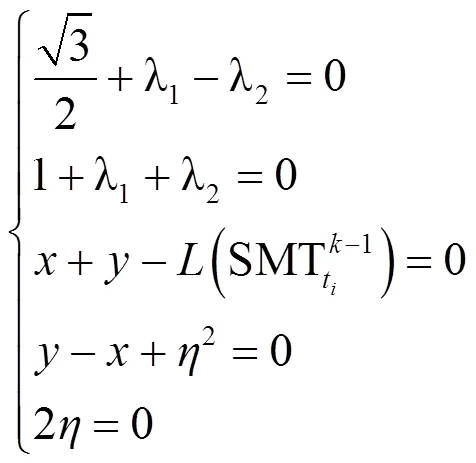
证明

证明

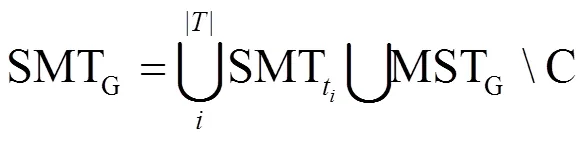
证毕。

证明

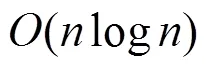
证毕。

7 仿真实验

本节利用工具NS2.34对策略RSFP、RRLC-GBP[13]、GSR[12]和OASS[1]进行性能比较。首先，将50~70个节点随机部署在一个2 000 m× 2 000 m的区域内。然后，分别通过固定节点个数变化半径的方式和固定半径变化节点个数的方式比较4种策略所消耗的平均中继节点数量。

如图2所示，各策略消耗的中继节点数量随着中继节点半径的增加而减少。本文提出的策略RSFP所需的中继节点数量明显少于其他3种策略。这是因为：首先，RRLC-GBP这种超区域中心部署节点的方式所生成的内接树的长度长于直骨架；其次，尽管策略OASS和GSR都采用基于直骨架的连接方式，RSFP构造的基于费马点的最短内接树更短（注：基于费马点的最短内接树是直骨架的一个特例）。如图3(a)所示，当中继节点半径等于50 m时，各策略所消耗的中继节点数量随着节点数的增加而增加。

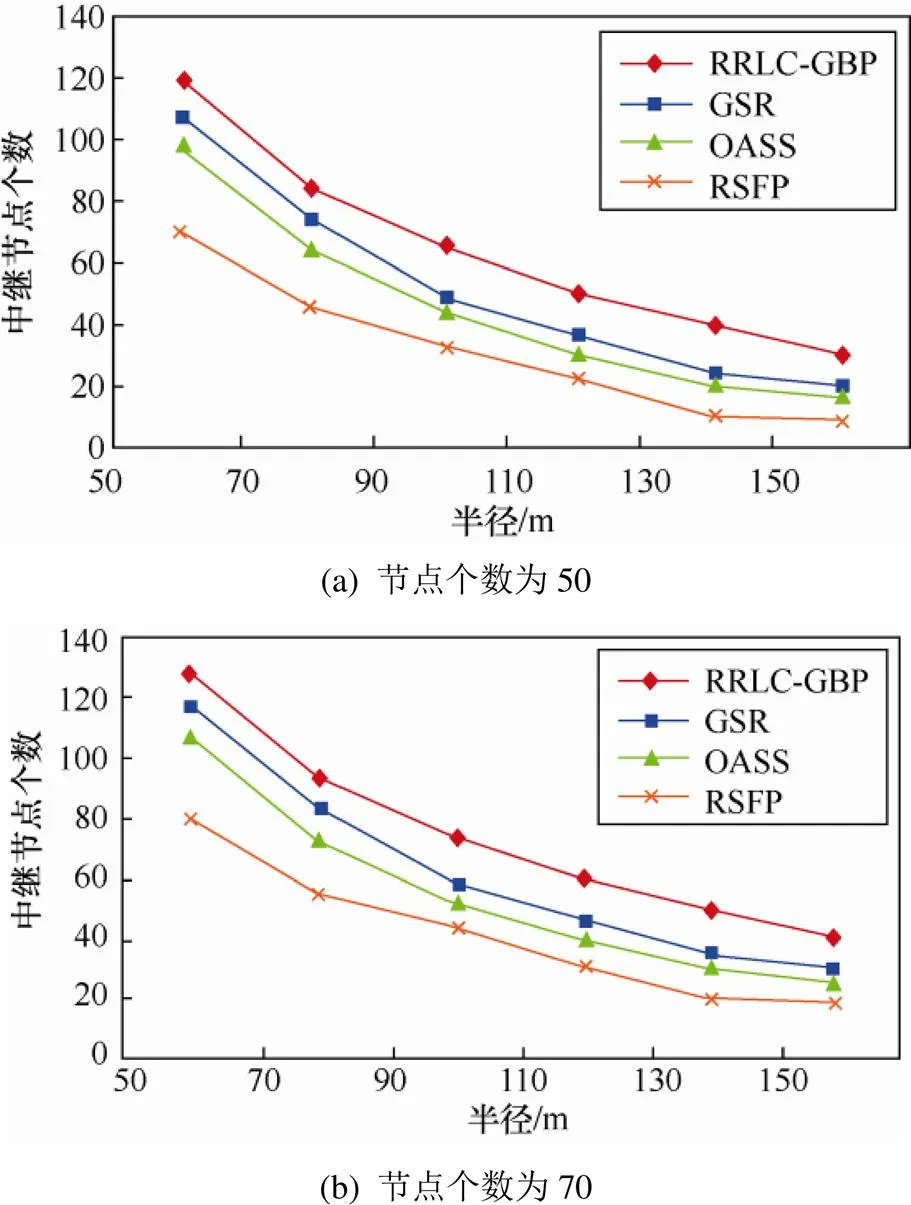
图2 节点个数为50、70时，各算法性能比较

在图3(b)中可以看到，当中继节点半径增加到100 m时，其消耗数量随着节点个数的增加呈现出先增后减的趋势。这是因为部署区域的大小固定，节点半径越大节点数量越多，那么更多的节点会直接相连。这意味着更少的节点需要通过部署中继节点的方式相连。此外，无论节点半径等于50 m或100 m，本文提出的策略RSFP所需的中继节点数量都是最少的。

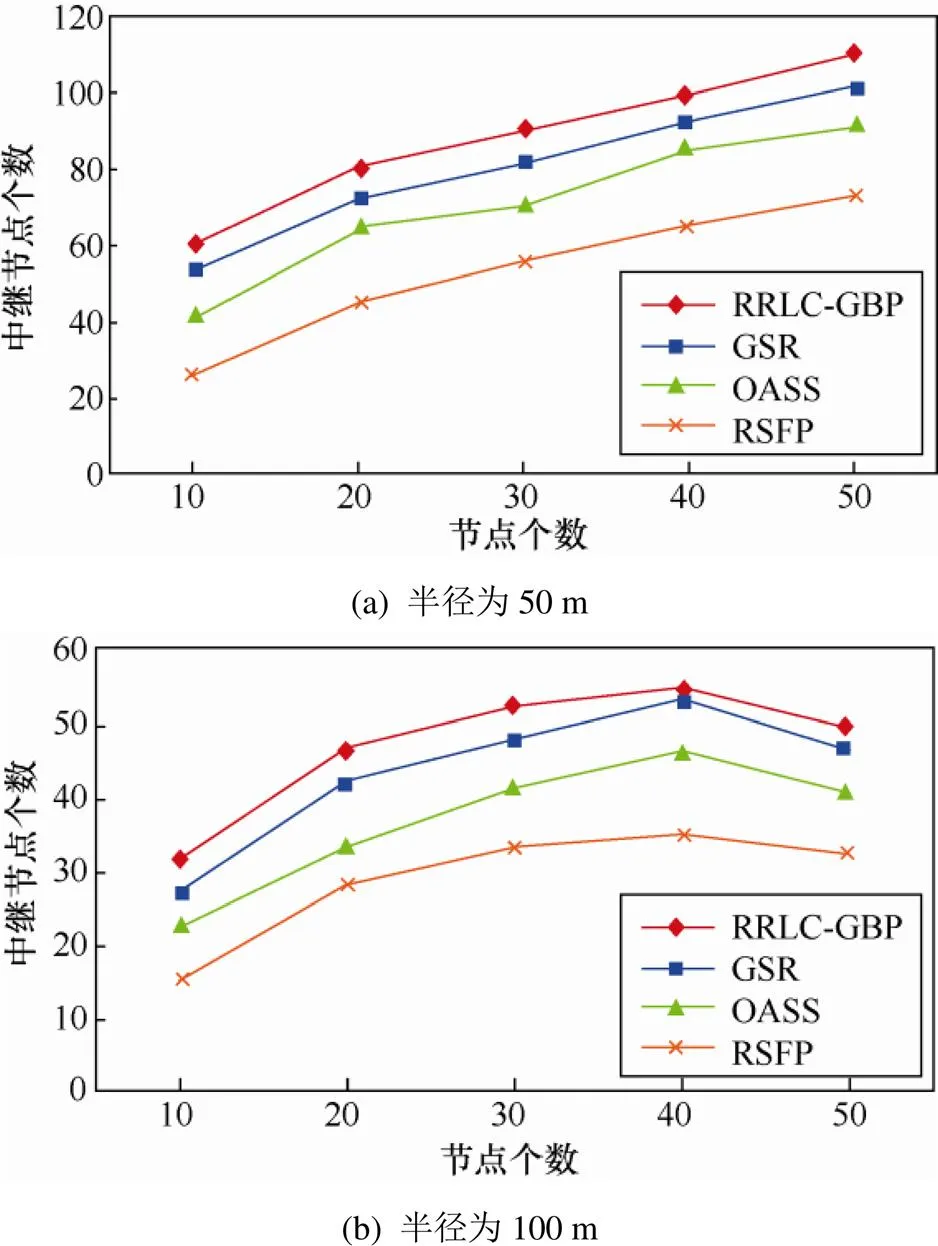
图3 半径为50 m和100 m时，各算法性能比较

8 结束语

[1] XIAODING W, LI X, ZHOU S M. A straight skeleton based connectivity restoration strategy in the presence of obstacles for WSN[J]. Sensors, 2017, 17(10):2299.

[2] LALOUANI W, YOUNIS M, BADACHE N. Optimized repair of a partitioned network topology[J]. Computer Networks, 2017, 128: 63-77.

[3] EFRAT A, FEKETE S P, MITCHELL J S B, et al. Improved approximation algorithms for relay placement[J]. ACM Transactions on Algorithms (TALG), 2016, 12(2): 20.

[4] WANG X D, LI X, ZHOU S M. Restoration strategy based on optimal relay node placement in wireless sensor networks[J]. International Journal of Distributed Sensor Networks, 2015, 11(7): 409085.

[5] MISRA S, MAJD N E, HUANG H. Approximation algorithms for constrained relay node placement in energy harvesting wireless sensor networks[J]. IEEE Transactions on Computers,2014, 63(12): 2933-2947.

[6] YANG D, MISRA S, FANG X, et al. Two-tiered constrained relay node placement in wireless sensor networks: computational complexity and efficient approximations[J]. IEEE Transactions on Mobile Computing, 2012, 11(8): 1399-1411.

[7] MISRA S, HONG S D, XUE G, et al. Constrained relay node placement in wireless sensor networks: formulation and approximations[J]. IEEE/ACM Transactions on Networking (TON), 2010, 18(2): 434-447.

[8] CHENG X, DU D Z, WANG L, et al. Relay sensor placement in wireless sensor networks[J].Wireless Networks, 2008, 14(3): 347-355.

[9] LLOYD E L, XUE G. Relay node placement in wireless sensor networks[J]. IEEE Transactions on Computers, 2007, 56(1): 134-138.

[10] TANG J, HAO B, SEN A. Relay node placement in large scale wireless sensor networks[J]. Computer Communications, 2006, 29(4): 490-501.

[11] CHEN D, DU D Z, HU X D, et al. Approximations for steiner trees with minimum number of Steiner points[J]. Journal of Global Optimization, 2000, 18(1): 17-33.

[12] JOSHI Y K, YOUNIS M. Exploiting skeletonization to restore connectivity in a wireless sensor network[J]. Computer Communications, 2016, 75: 97-107.

[13] RANGA V, DAVE M, VERMA A K. Relay node placement to heal partitioned wireless sensor networks[J]. Computers & Electrical Engineering, 2015, 48: 371-388.

[14] 陈洪生, 石柯. 基于四边形斯坦纳树的无线传感器网络连通恢复[J].计算机学报,2014,37(2):457-469. CHEN H S, SHI K. Quadrilateral steiner tree based connectivity restoration for wireless sensor networks[J]. Chinese Journal of Computers, 2014,37(2):457-469.

[15] SENEL F, YOUNIS M. Novel relay node placement algorithms for establishing connected topologies[J]. Journal of Network and Computer Applications, 2016, (70): 114-130.

[16] ROBINS G,ZELIKOVSKY A. Tighter bounds for graph Steiner tree approximation[J]. SIAM Journal on Discrete Mathematics, 2005, 19(1): 122-134.

Fermat point based connectivity restoration strategy in networks

ZHOU Zhaobin1,2, ZHANG Hongyan3, WANG Xiaoding1,2

1. College of Mathematics and Informatics, Fujian Normal University, Fuzhou 350117, China 2. Fujian Provincial Key Lab of Network Security & Cryptology, Fuzhou 350117, China 3. Concord University College, Fujian Normal University, Fuzhou 350117, China

network availability, connectivity restoration, triangulation, fermat point

周赵斌（1989− ），男，江西南昌人，福建师范大学实验师，主要研究方向为网络与信息安全和网络编码。

章红艳（1982− ），女，江苏南通人，福建师范大学讲师，网络安全与计算。

汪晓丁（1982− ），男，福建安溪人，博士，福建师范大学副教授，主要研究方向为网络与信息安全、无线通信网络、云计算与物联网。

TP393

A

10.11959/j.issn.2096−109x.2019048

2019−01−09；

2019−06−06

汪晓丁，wangdin1982@ fjnu. edu. cn

国家自然科学基金资助项目（No.61702103）；福建省自然科学基金资助项目（No.2016J01289）；福建省教育厅基金资助项目（No.JAT160123）

The National Natural Science Foundation of China (No.61702103), The Natural Science Foundation of Fujian Province(No.2016J01289), Fujian Provincial Education Department Project (No.JAT160123)

周赵斌, 章红艳, 汪晓丁. 基于费马点的网络连通性修复策略[J]. 网络与信息安全学报, 2019, 5(5): 32-38.

ZHOU Z B, ZHANG H Y, WANG X D. Fermat point based connectivity restoration strategy in networks[J]. Chinese Journal of Network and Information Security, 2019, 5(5): 32-38.