基于非对称直方图平移的可逆信息隐藏算法

何玉芬，殷赵霞，汤进，刘磊，黄石磊

基于非对称直方图平移的可逆信息隐藏算法

何玉芬1,2，殷赵霞1，汤进1，刘磊1，黄石磊3

（1. 安徽大学计算机科学与技术学院，安徽 合肥 230601；2. 六安市教学研究室，安徽 六安 237000；3. 深港产学研基地，广东 深圳 518057）

利用两个非对称直方图分别向相反方向平移嵌入信息，会产生像素值的补偿还原效应，提出了一种更好的像素值预测方法，生成两个更偏向0值右侧和左侧的非对称预测误差直方图，这样的两个直方图在进行第二层信息嵌入时，会出现更多的像素点恢复到原始图像像素值，减少图像扭曲失真，提高载密图像质量。与传统算法相比，减少了参与直方图修改的像素量，进一步保护了载密图像质量。

可逆信息隐藏；载密图像；预测误差；非对称直方图；直方图平移

1 引言

在当今网络飞速发展的信息化时代，网络图像日上传量日趋庞大，网络图像处理速度也越来越快。众所周知，图像可以作为数字隐写和数字水印的重要载体，进一步探究以图像为载体的可逆信息隐藏具有重要的意义。可逆信息隐藏技术不仅可以通过轻微修改载体数据的方式将信息嵌入载体，还可以无损恢复原始载体，在医学、军事、司法、艺术品珍藏等图像领域具有很大的运用价值，其典型应用在图像标注、图像完整性认证、篡改定位等方面。2009年，Tsai等[1]利用相邻像素之间的相似性提出了一种基于相邻像素预测误差直方图平移技术，该技术更好地利用图像像素的冗余性，提高直方图峰值点数量，解决传统基于图像像素直方图[2]峰值点的受限问题。该技术能嵌入更多的数据信息，同时在很大限度上减少了参与平移像素的数量，从而提高载密图像质量，被广泛应用于可逆信息隐藏研究。为了进一步提高图像像素的预测精度，增加直方图的高度，Sachnev 等[3]提出了基于预测误差扩展（PEE, prediction-error expansion）的一个代表性方法，通过4个相邻像素平均值的菱形预测方式统计预测误差直方图，提高信息的嵌入容量。Hong等提出了一种基于图像插值和光滑复杂区域检测[4]，以及采用误差能量估计器[5]减少不可嵌入的预测误差的数量，从而计算出高预测值的可逆信息隐藏方法，减少图像失真，提高载密图像质量。

以上几种可逆信息隐藏算法只是从提高直方图峰值点的数量上考虑，忽视了在保证相同峰值点的情况下如何进一步降低图像的失真。Chen等[6]于2013年提出了基于多预测机制的非对称直方图平移（AHS，asymmetric histogram shifting）技术，该算法思想是先按被预测像素左上方相邻3个像素的最小值预测方式，统计出最小值预测误差直方图h()，通过直方图平移（左平移）在峰值点处进行第一层信息的嵌入，生成载密图像1。接着在载密图像1中按被预测像素左上方相邻3个像素的最大值预测方式，统计出最大值预测误差直方图h()，按相反的方向（右平移）进行最大值预测误差直方图平移，在峰值点处进行第二层信息的嵌入，生成载密图像2，即最终的载密图像。该方法的创新之处在于，两种不同预测机制生成的非对称直方图向相反方向平移的过程中，上一层因嵌入信息被修改的部分像素值会在下一层嵌入信息时得到补偿后还原到原始像素值，而这些发生补偿还原的像素点处既嵌入了秘密信息又不发生平移扭曲，与传统算法相比，极大提高了载密图像的质量。2015年，Chen等[7]对AHS的可逆水印隐藏基本框架做了进一步研究，提出了通过多种像素预测机制统计像素的不同预测误差，利用两个对偶的非对称选择函数非对称地选择出合适的值，从而创建两个非对称直方图进行分层水印的嵌入，同理，利用分层嵌入过程中的像素补偿还原效应，使在高嵌入容量下具有较好的图像质量。2018年，Lyu等[8]对文献[6]算法进行实验，发现此方案在嵌入信息量达到最大时能够取得图像质量理论上的优化，但在嵌入信息量较少的情况下效果并不明显，进而提出了逐个像素点的分层嵌入信息方法，而不用等待全部像素点完成第一层嵌入后再开始进行第二层嵌入，该方法做到了在嵌入量较小时，比原有方法修改更少的像素点，提高了载密图像质量。

为了进一步发挥非对称预测误差直方图在平移过程中发生补偿还原效应，力求像素补偿还原量和像素修改量两者间达到较好的均衡，本文提出了一种新的像素预测机制方法，该方法在保证图像质量的前提下，相比文献[6]和文献[8]能更大地提高载密信息的嵌入量，而同时具有最小视觉失真。

2 本文算法

本节首先介绍了本文改进的算法思想、非对称直方图的创建和秘密信息的嵌入过程，然后介绍了利用本文算法对秘密信息进行提取和对原始图像进行完整恢复的过程。

2.1 算法思想

一般情况下，图像像素中3个相邻像素中的最小值比4个相邻像素中的最小值大，3个相邻像素中的最大值比4个相邻像素中的最大值小。如果按照4个相邻像素最小值和最大值的方式来预测像素值（如图1所示），最小值预测误差直方图比基于3个相邻像素的最小值预测方式[6-8]（如图2所示）产生的预测误差直方图更偏向0值点右侧；而最大值预测误差直方图比基于3个相邻像素最大值预测方式[6,8]产生的预测误差直方图更偏向0值点左侧。一方面，产生的两个非对称直方图分别向两个相反方向移动的过程中，会有更多的像素恢复到原始像素值，显然在提高图像质量方面有了改进；另一方面，以512×512×8位灰度图像为例，本文方法生成的预测误差矩阵大小为511×510，而文献[6]和文献[8]方法生成的预测误差矩阵大小为511×511，本文方法减少了参与直方图平移的像素量，降低了平移扭曲，再一次提高了载密图像质量。

图1 4个相邻像素预测的改进方式

图2 原始3个相邻像素预测方式

为了更好地体现非对称直方图平移算法的优点，将嵌入的秘密信息平均分成两部分，通过非对称直方图平移分别嵌入载体图像中，具体嵌入过程见2.3节。

2.2 创建非对称预测误差直方图

传统的基于预测误差直方图可逆信息隐藏是基于一种像素预测机制方式，对原始图像统计形成的预测误差直方图都是以0为中心，两边分布相似对称的拉普拉斯分布直方图（如图3所示）。本文介绍的方法是基于两种不同预测机制方式，创建出更为右偏和左偏两种不对称预测误差直方图，两次嵌入秘密信息过程中会发生像素点的补偿还原效应，在嵌入容量大的情况下，这种效应更为明显。

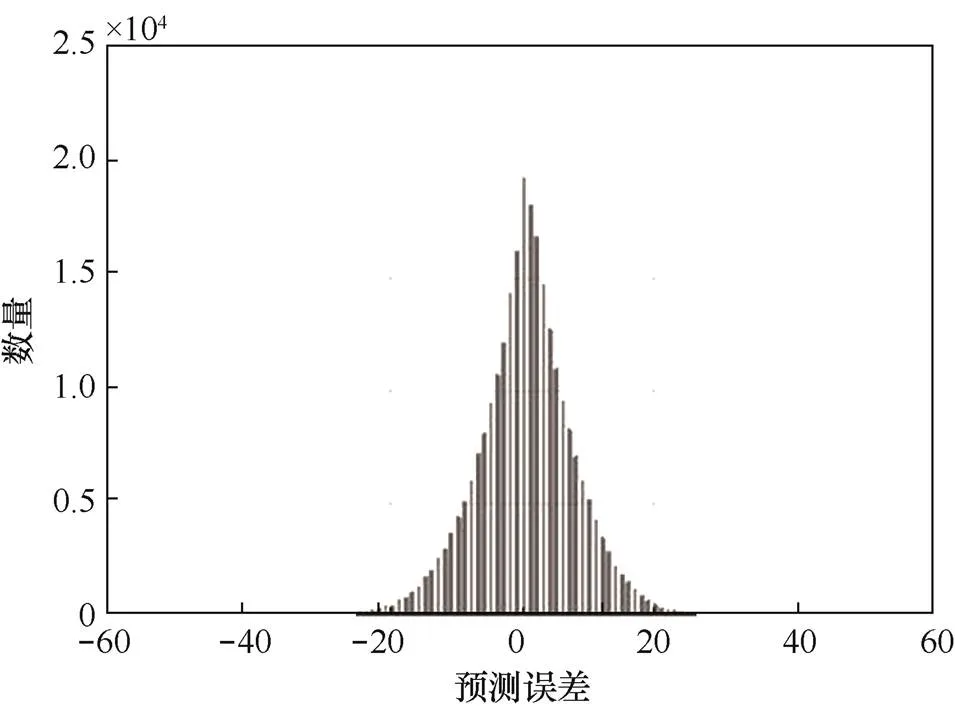
图3 基于菱形预测方法的elaine图像预测误差直方图

按图1方式访问所有被预测像素，遍历其相邻的左上方4个像素计算其预测值，第一次秘密信息嵌入时取4个相邻像素中的最小值作为该像素的预测值，计算当前像素的预测误差，预测误差值由式(1)计算。

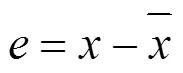
其中，代表预测误差值，代表当前像素值,`代表当前像素的预测值。在产生的最小值预测误差直方图h()（如图4所示）中，进行左方向平移嵌入前一半的秘密信息，生成载密图像1。在载密图像1像素矩阵中按图1的方式访问所有被预测像素左上方4个相邻像素计算其预测值，第二层嵌入过程是取4个相邻像素中的最大值作为该像素的预测值，根据式(1)计算当前像素预测误差，产生所有被预测像素最大值预测误差直方图h()（如图5所示），该直方图进行右方向平移嵌入剩下的一半秘密信息。

其中，p、z分别是图4中的峰值点和左侧零值点，pz分别是图5中的峰值点和右侧零值点。

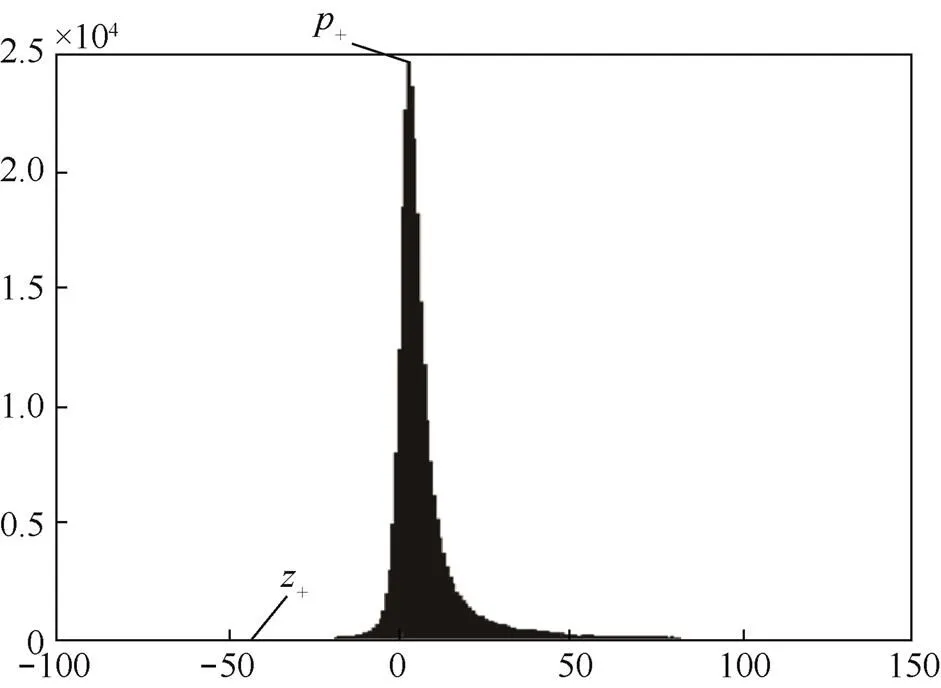
图4 本文方法取最小值作为预测值生成的Lena图像预测误差直方图

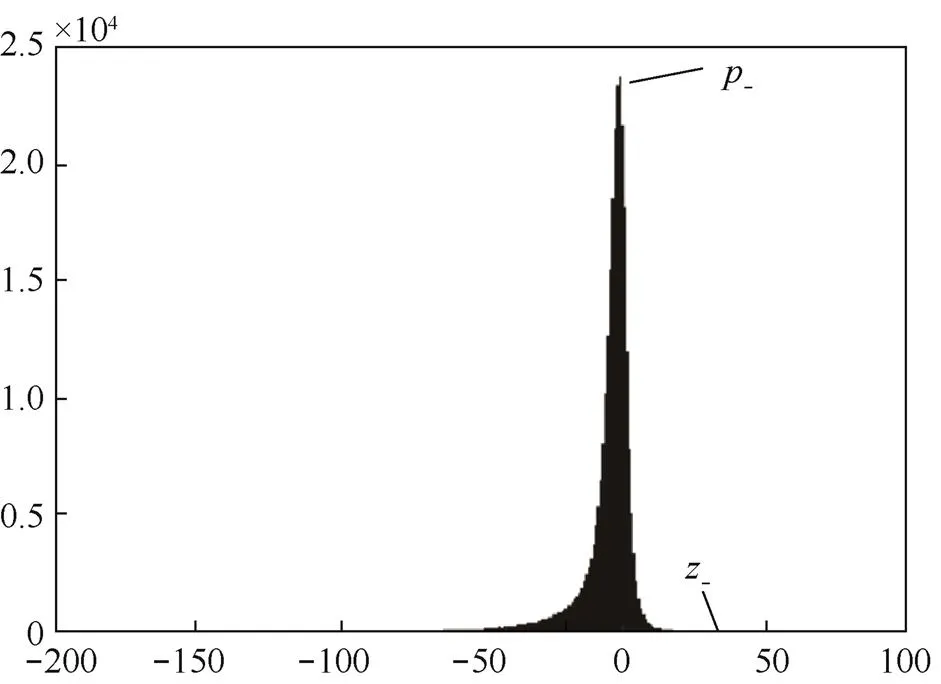
图5 本文方法取最大值作为预测值生成的Lena图像预测误差直方图

2.3 嵌入过程

对于一张尺寸为的8位灰度图像，用x表示第行第列处像素值，有x∈[0,255]。在秘密信息嵌入过程中存在发生像素值上溢和下溢的可能，如像素值为0和255的像素点有可能经过直方图平移之后分别被修改为−1和256。为了解决这个问题，采用位置图标志：分别按行按列扫描图像，在直方图向左平移过程中，一旦遇到像素值为0的像素点，便记录此处的坐标放入位置信息中；直方图向右平移过程中，一旦遇到像素值为255的像素点，记录此处的坐标放入位置信息中。将添加到秘密信息的尾部，作为秘密信息一并嵌入。嵌入过程中不对发生溢出位置的像素进行操作。嵌入过程的描述如下。

1) 取灰度图像第一行第一列和最后一列的像素作为参考像素。

2) 对于2,21，像素x通过与其相邻左上方4个像素x，1、x11、x1，、x1，计算其预测值，分别计算出左、左上、上、右上预测误差eleueder，计算方法如下。

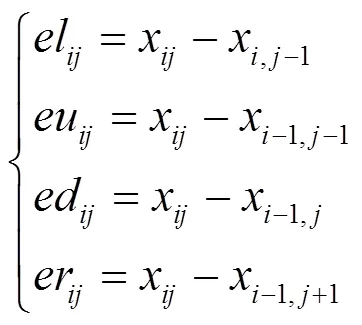
因为第一层秘密信息的嵌入是取相邻像素最小值作为预测值，故取eleueder中的最大值作为像素x的预测误差，记为e，做如下计算。

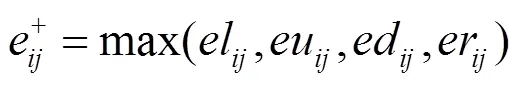
通过所有被预测像素的预测误差e矩阵产生了偏向于0值右侧的不对称预测误差直方图h()，如图4所示。

3) 再次扫描图像，通过不对称预测误差直方图h()（如图4所示）平移进行秘密信息的嵌入，对于像素x，在进行前一半秘密信息嵌入后得到载密图像，对于y处的像素值，可以通过式(4)计算，表示嵌入的秘密信息。

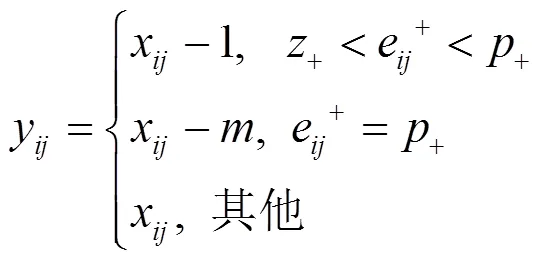
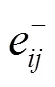
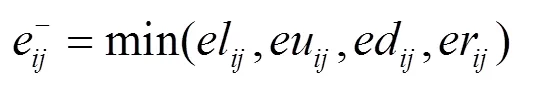
eleueder分别是像素y与其相邻左上方4个像素y,1、y1,1、y1,、y1,1的预测误差值。通过直方图h()（如图5所示）平移实现秘密信息的第二层嵌入。对于载密图像任意像素y（去除参考像素），进行后一半秘密信息的嵌入，得到最终的载密图像，z处的像素值可以通过式(6)计算，表示嵌入的秘密信息。

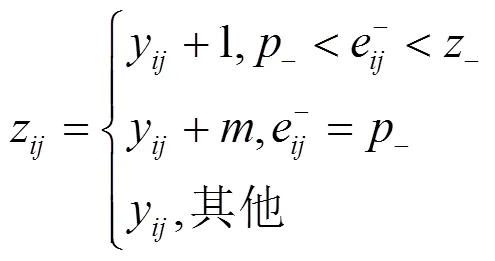
至此，两层嵌入的秘密信息序列长度之和即总的信息嵌入量。

2.4 提取过程

为了提取秘密信息并从载密图像中恢复原始图像，采取如下的逆操作过程。

1) 初始化最终恢复的图像=，取第一行第一列和最后一列的像素作为参考像素。

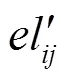
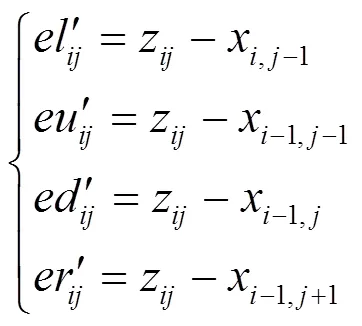
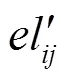
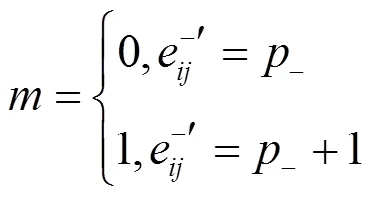
第一次提取后的图像任意像素y的值可以通过式(9)计算得到。

4) 通过4个相邻像素y,1、y1,1、y1,、y1,1按式(2)继续计算图像任意像素y的预测误差值eleueder，通过式(3)取得4个预测误差值中的最大值，用式(10)提取第一层嵌入的秘密信息，表示提取的秘密信息。

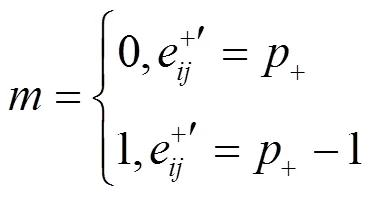
至此，所有的秘密信息被提取，在提取出的秘密信息尾部可以得到位置信息，保证位置信息中记录位置处的像素值保持不变。

3 实验结果

3.1 嵌入容量和图像质量的比较

为了评估本文方法在多次测试实验中的可行性，实验选取了USC-SIPI 图像数据库中的多张标准灰度图像作为测试图像。实验结果呈现了本文预测机制算法较之前两种算法[6-8]的优越性，取得了预期实验效果。本节以Baboon、barbara、Jet、Lena、Peppers、Sailboat（如图6所示）6张测试图像进行3种算法的率失真性能对比实验，图7是实验结果的峰值信噪比曲线对比。

图6 测试图像

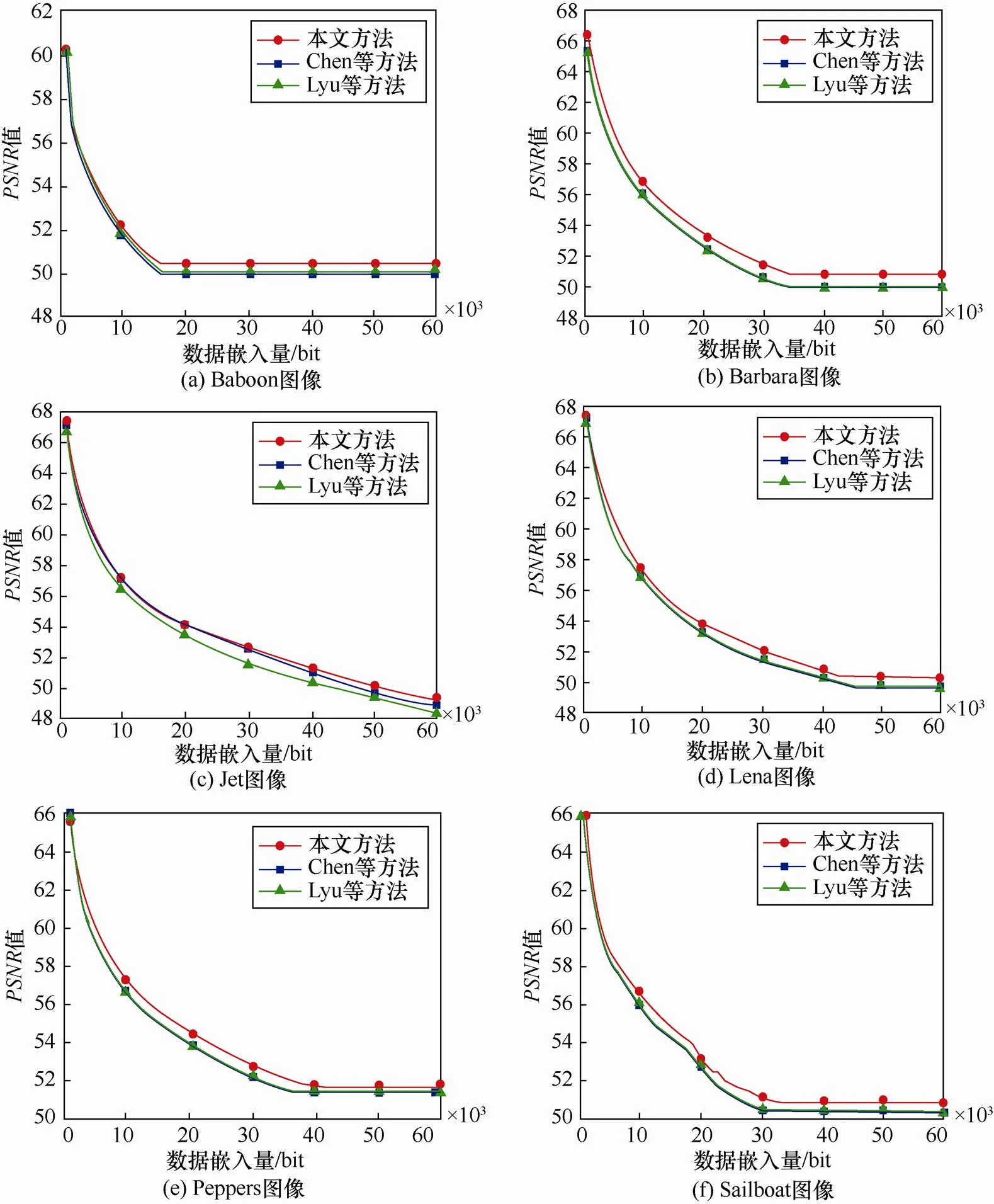
图7 图像的率失真对比

载密图像虽然视觉上感觉不到变化，但和原始图像有不同，为了衡量嵌入秘密信息后图像的质量，通常会参考峰值信噪比（PSNR，peak signal to noise ratio）的值来评定结果是否令人满意。PSNR的值越大，代表载密图像较原始图像的失真程度越小，图像的质量越高。6张测试图像在3种算法下的峰值信噪比曲线对比表明，随着信息嵌入量增加，原始图像中需要修改的像素点越多，使载密图像的质量逐渐下降。从图7中可以看出，在相同嵌入容量的情况下，本文方法生成的载密图像质量高于另两种方法。实验中，3种方法在不同嵌入容量情况下6张测试图像的PSNR值如表1～表3所示。一般情况下，随着嵌入容量的增大，本文方法效果较为明显。

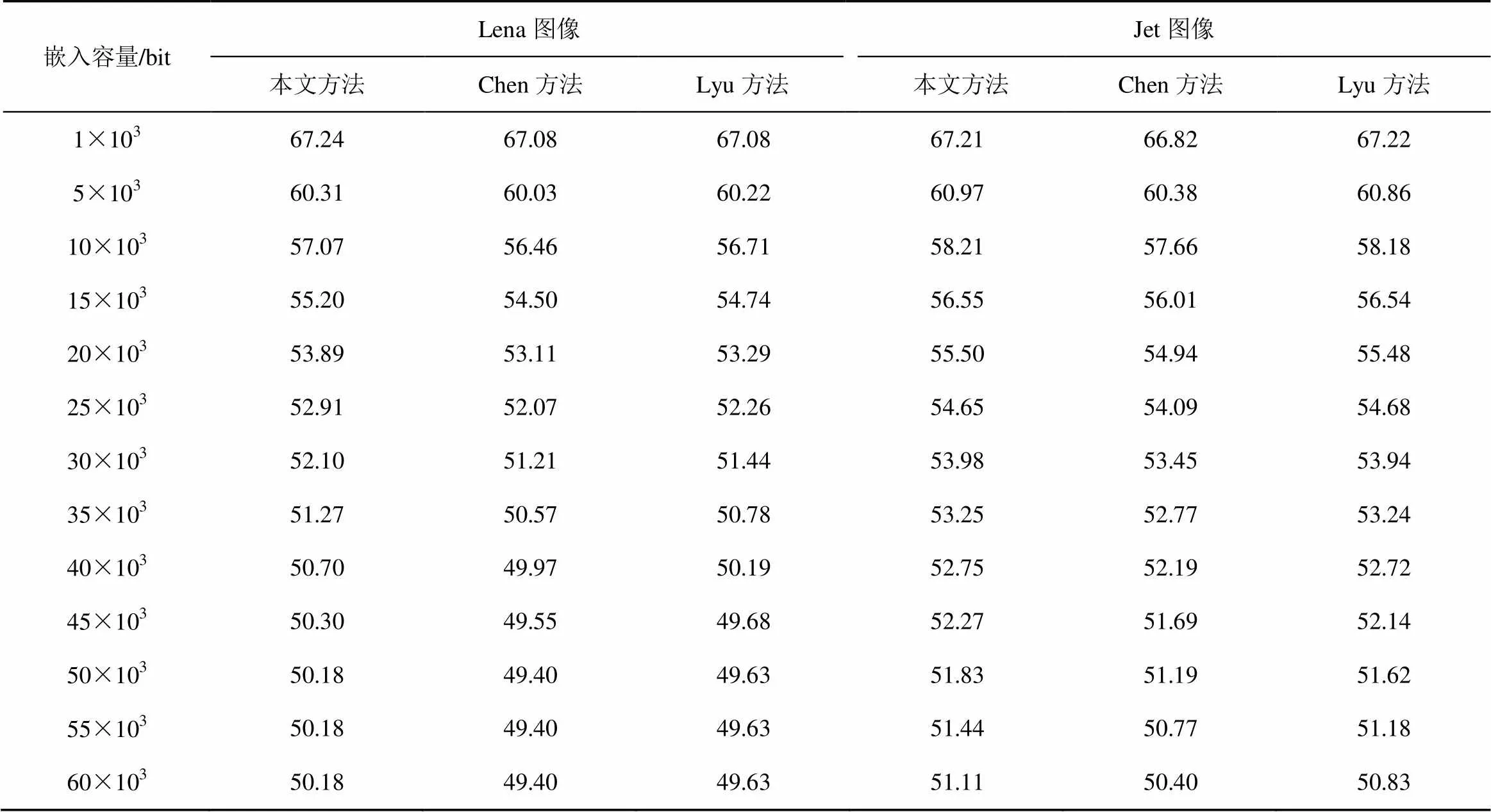
表1 Lena、Jet图像在不同嵌入量情况下PSNR值的对比

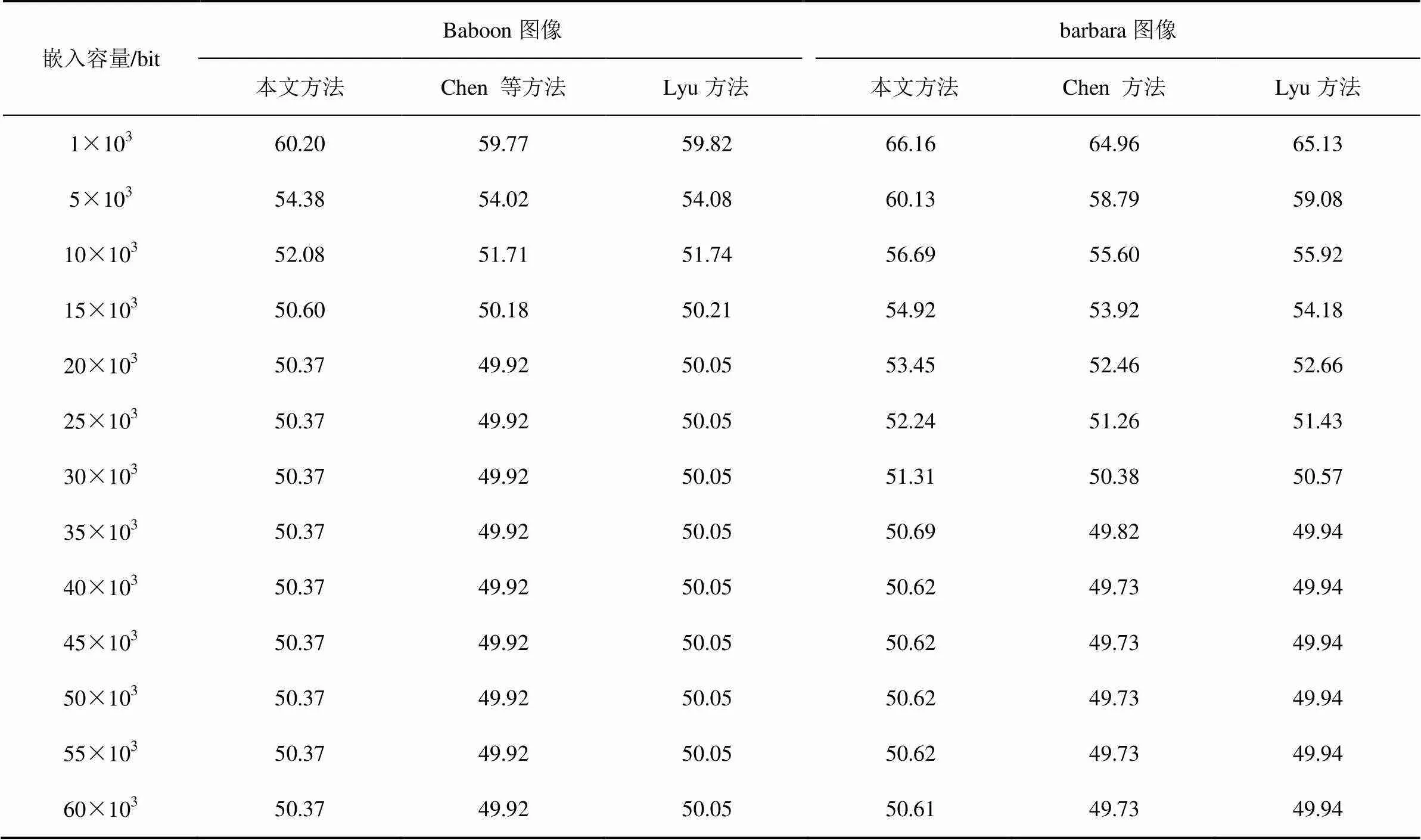
表2 Baboon、barbara图像在不同嵌入量情况下PSNR值的对比

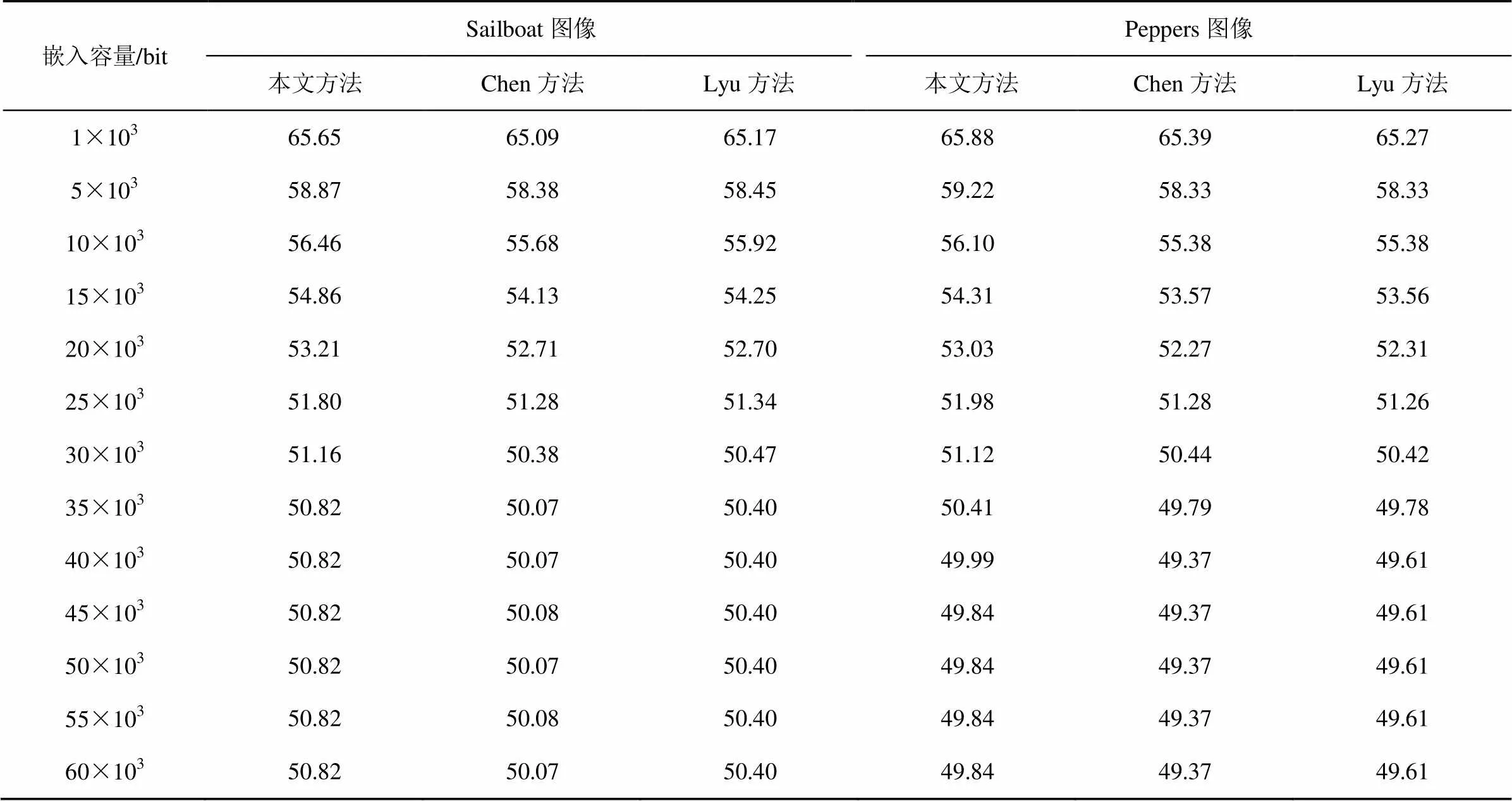
表3 Sailboat、Peppers图像在不同嵌入量情况下PSNR值的对比

3.2 像素还原量、修改量及PSNR值的对比

通过多个图像的相同实验，实验结果（如表1～表3数据所示）表明本文方法优于另两种方法[6-8]。为了进一步探究该算法优越性的原因所在，实验中记录了在不同信息嵌入量情况下3种方法发生的像素补偿还原量和像素修改量情况。图8显示的是在 40 000bit嵌入量情况下发生补偿还原像素量、像素修改量及PSNR值间的对比，通过柱形图8可以看出，本文方法在每张测试图像中发生的像素修改量比另两种方法都低，发生的像素补偿还原量有的甚至高于另外两种方法。虽然有的测试图像发生的像素补偿还原量略低于另外两种方法，但其像素修改量却比另外两种方法低得多，这也解释了为什么本文算法得到的实验结果PSNR值是最高的，生成的载密图像质量是3种方法中最好的。

通过多组实验数据的比较分析，本文方法效果明显的主要原因在于该方法发生的像素补偿还原量和像素修改量两者之间能达到较好的均衡，也就是说，在保证一定像素修改量的情况下能达到像素补偿还原量的最佳值，而在满足一定像素补偿还原量的情况下又能达到像素修改量的最小值。表4列出了3种方法在60 000bit嵌入量情况下像素的还原量、修改量以及对应载密图像PSNR值的具体实验数据。表中数据显示，图像Baboon、 Peppers、Sailboat在本文方法实验中发生的像素补偿还原量是3种方法中最多的，同时发生的像素修改量又是最少的，显然图像质量是最优的。通过表4数据还可看出，Chen方法在图像Lena、Jet、barbara实验中发生的像素补偿还原数量虽然较本文方法稍多些，但在两次秘密信息嵌入的过程中发生像素的修改量却较多。以barbara图像为例，本文方法发生的像素修变量为152 831 bit，Chen方法发生的像素修改量为187 411 bit，修改量相比幅度更大，导致其PSNR值偏低，而Lyu方法在所有测试图像中发生的像素补偿还原量不及本文方法多，而发生的像素修改量却明显增多，故其PSNR值低于本文方法。通过以上分析得出，本文方法在所有测试图像中发生的像素补偿还原量和像素修改量两者之间的均衡度高于另外两种方法。

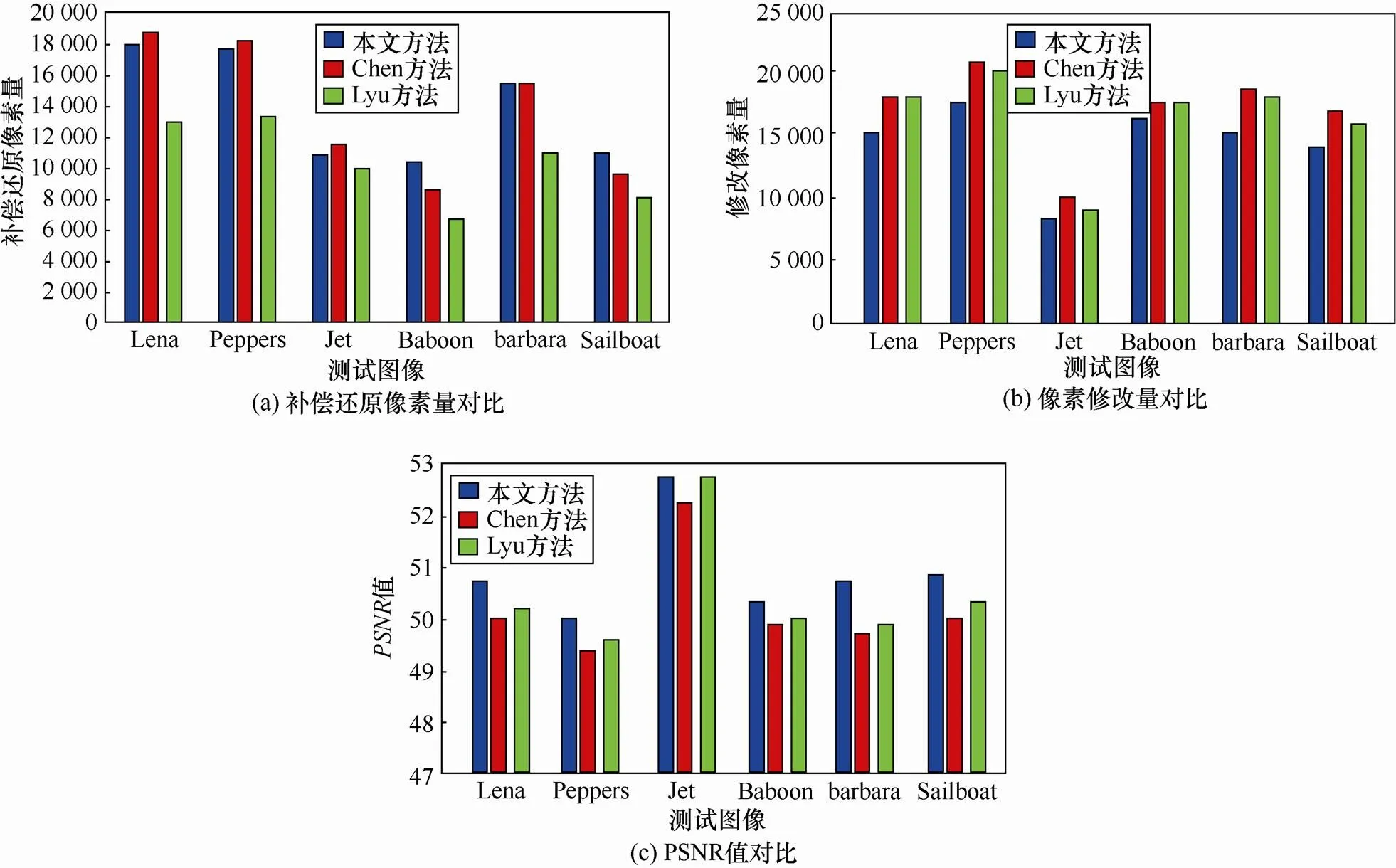
图8 40000bit嵌入量下发生补偿还原像素量、修改量及PSNR值的对比

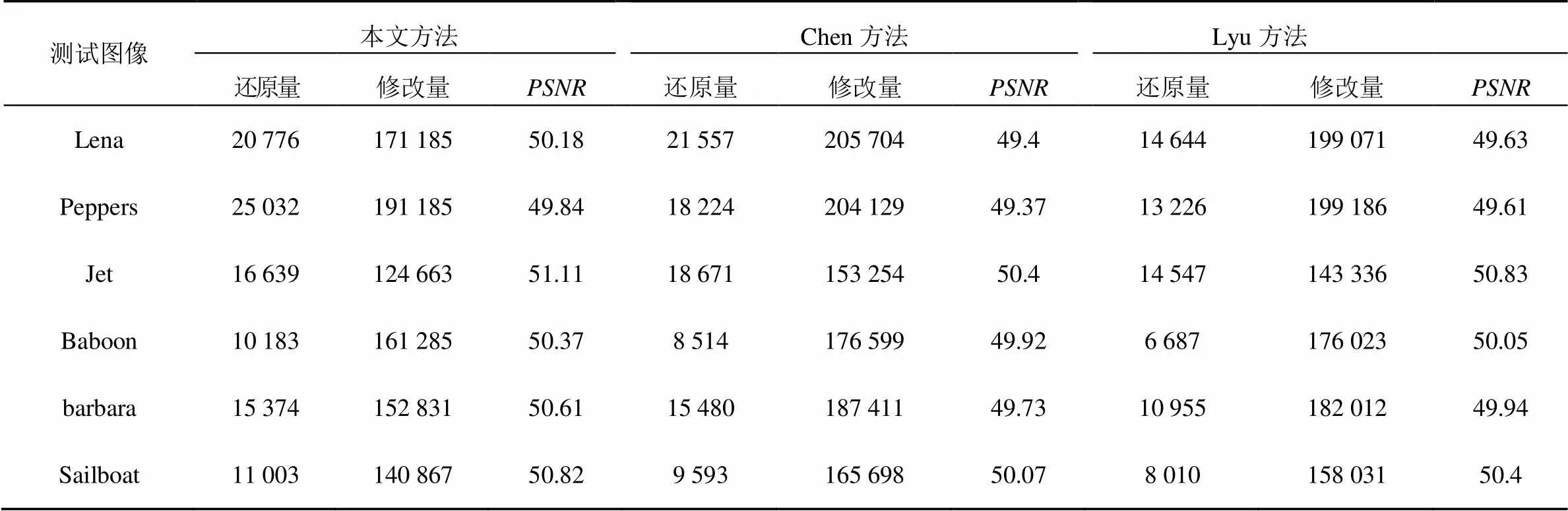
表4 60 000bit嵌入量情况下发生像素还原量、修改量及PSNR值的对比

实验数据证实，本文方法在不同嵌入容量下PSNR值始终高于另外两种方法，所以本文方法在大多数情况下能很好地体现AHS技术的补偿还原效应。

4 结束语

与传统单直方图平移相比，两个非对称直方图通过向相反方向的平移，在分层嵌入秘密信息的过程中使一部分像素补偿还原到原始像素值，降低了图像像素的修改量，提高了载密图像质量。本文提出了一种新的基于图像相邻像素预测方式的非对称直方图平移的可逆信息隐藏算法，通过该算法，在两层信息嵌入过程中发生像素补偿还原的机会更大，满足像素修改量在一定范围内的情况下，恢复原始图像像素值的点更多，提高了载密图像的质量，很好地体现出非对称直方图平移算法的优点。实验中发现，非对称直方图平移的优势还可以进一步挖掘、探讨更高精度的预测机制、选择更好的峰值点、减少平移像素扭曲等方面都值得今后进一步研究。

[1] TSAI P, HU Y C, YEH H L. Reversible image hiding scheme using predictive coding and histogram shifting[J]. Signal Processing, 2009, 89(6):1129-1143.

[2] NI Z, SHI Y Q, ANSARI N, et al. Reversible data hiding[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2006, 16(3): 354-362.

[3] SACHNEV V, KIM H J, NAM J, et al. Reversible watermarking algorithm using sorting and prediction[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2009, 19(7):989-999.

[4] HONG W, CHEN T S. Reversible data embedding for high quality images using interpolation and reference pixel distribution mechanism[J]. Journal of Visual Communication & Image Representation, 2011, 22(2):131-140.

[5] HONG W. Adaptive reversible data hiding method based on error energy control and histogram shifting[J]. Optics Communications, 2011, 285(2):101-108.

[6] CHEN X, SUN X, SUN H, et al. Reversible watermarking method based on asymmetric-histogram shifting of prediction errors[J]. Journal of Systems & Software, 2013, 86(10):2620-2626.

[7] 陈先意, 孙星明. 基于非对称预测误差直方图平移的可逆水印基本框架研究[C]//第十二届全国信息隐藏暨多媒体信息安全学术大会论文集. 2015.

CHEN X Y, SUN X M. General framework of reversible watermarking based on asymmetric histogram shifting of prediction error[C]//The 12th China Information Hiding Workshop.2015.

[8] 吕志恒, 刘磊, 陈思, 等. 基于非对称直方图修改的可逆信息隐藏方案[J]. 网络与信息安全学报,2018, 3(5) 30: 73-79.

LYU Z H, LIU L, CHEN S, et al. Reversibel data hiding scheme based on asymmetric histogram modification[J]. Chinese Journal of Network and Information Security,2018, 3(5) 30: 73-79.

Reversible data hiding algorithm based on asymmetric histogram shifting

HE Yufen1,2,YIN Zhaoxia1,TANG Jin1, LIU Lei1,huangshilei3

1. School of Computer Science and Technology, Anhui University, Hefei 230601,China 2. Liu 'an Teaching and Research Office, Liu’an 237000, China 3. PKU-HKUST Shenzhen Hong Kong Institution, Shenzhen 518057, China

The shifting of two asymmetric histograms in opposite directions in data embedding respectively had produced the pixel compensation and restore effect, a better reversible data hiding algorithm based on pixel prediction was proposed, two asymmetric histograms of prediction error were generated on the more right and the more left side of zero value,when they were shifed in the seconddata embedding stage, more pixels would be restored to the original image pixel value to reduce image distortion and improve the image quality. Compared with the traditional algorithm, it reduces the amount of pixels involved in the histogram shifting and protects the quality of secret image.

reversible data hiding, secret image, prediction error, asymmetric histogram,histogram shifting

何玉芬（1985− ），女，安徽黄山人，安徽大学硕士生，六安市教学研究室教研员，主要研究方向为基于数字图像的可逆信息隐藏。

殷赵霞（1983− ），女，安徽太湖人，博士，安徽大学副教授、博士生导师，主要研究方向为智能媒体安全与取证、信息隐藏、伪装与保密、大数据隐私保护。

汤进（1976− ），男，安徽合肥人，博士，安徽大学教授、博士生导师，主要研究方向为计算机视觉、深度学习、多媒体大数据处理。

刘磊（1997− ），男，安徽六安人，主要研究方向为数字图像可逆信息隐藏、视觉跟踪。

黄石磊（1979− ），男，湖南益阳人，博士，深港产学研基地副研究员、高级工程师，主要研究方向为信号处理、信息系统、语音信号处理、语音识别。

TP309

A

10.11959/j.issn.2096−109x.2019053

2018−12−11；

2019−03−20

黄石磊，shilei.hung@imsl.org.cn

深圳市基础研究（学科布局）基金资助项目（No.JCYJ20170817160058246）；国家自然科学基金资助项目（No.61872003）

Shenzhen Basic Research (Subject Layout)( No.JCYJ20170817160058246), The National Natural Science Foundation of China (No.61872003)

何玉芬, 殷赵霞, 汤进, 等. 基于非对称直方图平移的可逆信息隐藏算法[J]. 网络与信息安全学报, 2019, 5(5): 80-89.

HE Y F, YIN Z X, TANG J, et al. Reversible data hiding algorithm based on asymmetric histogram shifting[J]. Chinese Journal of Network and Information Security, 2019, 5(5): 80-89.