基于直通式迷宫密封的海上平台井口装置研究
2019-10-17余焱群张懿萱2康玉晶
余焱群,张懿萱2,康玉晶
(1.中国石油大学 机电工程学院,山东 青岛 266580;2.北京交通大学 威海分校通信工程系,山东 威海 264401)
引言
国内海上油田的主产区从上世纪的南海北部油田逐渐过渡为以渤海油田为主[1-3],而渤海油区的大型油田(地质储量大于1亿吨)以稠油为主,储量占到已发现石油总储量的85%。因此,研究稠油的开发方式,在渤海海域的油田开发中占有举足轻重的地位。项目组在海上稠油油田试推有杆泵人工举升工艺,井口安全是新工艺实施的前提。
在海上平台生产设施发生火警、管线破裂及发生不可抗拒的自然灾害等非正常情况时,需要紧急关闭井口,防止井喷,保证油气井安全,因此海上油井的安全系统要求远远高于陆地油井[4-6],目前国内外还没有适用于平台的开放式井口设备。
1 海上平台复合井口装置
复合井口装置主要包括两大机构,上部为盘根式可调心井口结构,下部为断杆自动关井、手动封井井口结构,整体结构如图1所示。上部结构主要完成正常作业时光杆动态密封和自动调偏功能[7]。下部结构分成上下两层,下层主要由压缩弹簧和闸板组成,光杆脱断后压缩弹簧推动左右闸板,左右闸板配合封堵井口,实现快速、自动关井功能;上层主要由丝杆和密封本体组成,停泵封井时,旋转螺杆推动密封本体抱紧光杆、密封井口,此时上部盘根井口机构处于静态密封状态;其中手动关井机构结构和可靠性是实现关井的前提,内部液体密封结构及漏失理论研究是基础。

1.盘根压帽 2.压套 3.盘根盒 4.盘根 5.球头 6.球头压盖 7.球头座 8.密封本体 9.螺杆 10.关井闸板 11.压缩弹簧图1 海上平台复合井口装置
2 井口密封泄漏模型
油井停井后,关井机构才会动作,密封本体与光杆之间相对静止,极端工况下会出现相对滑动,但是滑移量和速度较小。基于上述工作状况,海上平台井口密封装置采用直通式迷宫密封模式,结构模型如图2所示。

图2 井口迷宫密封物理模型图
图2中,pi,po分别为进口油压、出口油压,MPa;Hc,Lc分别为密封齿槽深度、齿槽宽度,mm;H,L分别为间隙高度、密封齿宽度,mm。
泄漏液流在迷宫中流动时,因液体黏性而产生的摩擦,使流速减慢、流量(泄漏量)减少。流体沿流道的沿程摩擦和局部磨阻构成了磨阻效应,前者与通道的长度和截面形状有关,后者与迷宫的弯曲数和几何形状有关[8-9]。
2.1 间隙、密封齿槽中损失
设迷宫泄漏量为Q(m3/s),根据流体动力学理论[10-11],则间隙中的流速为:
(1)
式中,A1—— 间隙环空的截面积,mm2
d—— 光杆直径,mm
密封齿槽中的流速为:
(2)
式中,A2为齿槽环空的截面积,mm2。
间隙及密封槽中的总沿程损失为:
(3)
式中,n—— 密封级数
λ1—— 间隙中的沿程阻力系数
λ2—— 密封槽中的沿程阻力系数
de1—— 间隙处的当量直径,mm
de2—— 密封齿槽处的当量直径,mm
2.2 局部损失
流体通过迷宫缝口,流束的截面减小,会因惯性的影响而产生收缩,出现流束收缩效应;而进入密封槽时,流速的截面膨胀,产生动能耗散作用[12]。每级密封,流体均经历从小截面管道流向大截面管道,然后再进入小截面管道,局部损失为:
(4)
2.3 迷宫泄漏模型
综合式(3)、式(4),直通式迷宫井口结构,泄漏流体总的水头损失ha为:
ha=hf+hj
(5)
泄漏流体总的压强损失为:Δp=ρgha
(6)
整理后得井口密封结构总的泄漏模型为:
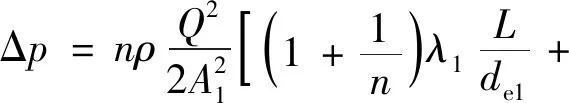
(7)
3 迷宫结构参数确定
研究各参数与Q,Δp关系时,可设n=1考虑。
3.1 间隙长度
数学模型式(7)中的第一项是液体过间隙的压降,后两项是有密封槽后的压降,分析数学模型的第一项可以分析间隙对泄漏量的影响。
间隙泄漏流体的压强损失:
(8)
对于d=28 mm,Δp=5 MPa,不同间隙H下,泄漏量Q与间隙长度L的关系如图3所示。

图3 泄漏量Q与间隙长度L的关系
由图3可知,随着间隙H的增大泄漏量Q随之增大,同一间隙量H下Q值随间隙长度L的增大急剧减小,各曲线变化趋势相同。L=4 mm时泄漏量Q下降了97.5%,间隙长度超过4 mm后基于增加间隙长度的方式减小间隙泄漏量Q意义不大。
3.2 密封槽参数
基于数学模型式(7),设d=28 mm,Δp=5 MPa,H=0.1 mm,L=4 mm,一级密封总体长度相同的情况下,泄漏量Q与密封槽深宽比k(k=Hc/Lc)关系如图4所示。

图4 泄漏量Q与槽深宽比k的关系
据图4,整体上槽宽Lc增加泄漏量Q增加;同一Lc值下,泄漏量Q先急剧增加,到极值后回落,最后趋于平稳。这是由于在泄漏压力及间隙较小的情况下,流体在间隙内流动以层流为主,由湍流部分消耗的能量极少,流动主要能量消耗是由间隙边界表面与流体摩擦力引起,当凹槽宽度增大会使间隙的有效长度减小,流体摩擦损失的能量减少而致使泄漏量增大。深宽比k>0.3后,k值对泄漏量Q的影响不大,据此可取k=1/3。
数学模型式(7)中的第2,3项表达密封槽对泄漏量的影响,整理得:

(9)
基于数学模型式(7),设d=28 mm,Δp=5 MPa,L=4 mm,k=1/3,泄漏量Q与密封槽深Hc之间的关系如图5所示。
由图5可知,随Hc增大泄漏量Q值会出现一个峰值,且随着H值增大峰值右移。对于磨损量1 mm曲线,槽深Hc=2 mm时泄漏量Q相对峰值下降90%,Hc从2 mm增加到3 mm,泄漏量Q仅下降1.5%,而槽宽Lc将增加50%,故确定密封槽参数:Hc=2 mm,Lc=6 mm。

图5 泄漏量Q与密封槽深Hc的关系
3.3 密封级数
基于参数H=0.1 mm,d=28 mm,L=4 mm,Hc=2 mm,Lc=6 mm,Δp=5 MPa,得到泄漏量Q与密封槽深n的关系曲线如图6所示。

图6 泄漏量Q与密封级数n的关系
随着密封级数n增加,泄漏量Q快速减少,最后趋于平缓。由图6可知,迷宫级数从4级提高到5级,泄漏量下降不到2%,由此可见迷宫级数超过4级后,继续提高迷宫级数来减小泄漏量效果有限。
4 迷宫密封关井整体结构
对于光杆直径d=28 mm的配套井口,基于数学模型确定直通式迷宫密封结构:L=4 mm,Hc=2 mm,Lc=6 mm,n=4,密封本体构件结构图如图7所示。
若光杆磨损0.1 mm,井口出现10 MPa的高压时,流体通过图7本体结构组成的如图1所示井口直通式迷宫机构时,基于泄漏模型可得泄漏量为2.728×10-5m3/s,可见泄漏量较小,结合井口盘根密封可以很好的实现海洋平台封井撤离海洋平台的目的。

图7 迷宫密封本体结构图
5 结论
井口安全是封井撤离海洋平台的前提,设计了直通式迷宫密封井口机构,基于流体动力学理论建立了流体泄漏模型,详细研究了各结构参数对流体泄漏量的影响,确定了密封本体结构,在0.1 mm间隙,10 MPa 井口高压下,泄漏量为2.728×10-5m3/s。形成了海上平台复合井口装置,可实现正常作业动态密封、断杆自动关井、手动封井等功能。
