柏叶口水库泄洪发电洞掺气水流对挑距的影响分析
2019-10-17
(山西省柏叶口水库建设管理局,山西 太原 030002)
1 概 述
柏叶口水库位于山西省交城县文峪河干流上,总库容10137万m3,其中防洪库容2166万m3,调洪库容2457万m3;水库死水位1080.00m,正常蓄水位1133.00m,防洪限制水位1128.00m,防洪高水位1135.26m,设计洪水位1135.26m,校核洪水位1136.22m。
水库于2015年底竣工验收,在管理运行中发现:当泄洪发电洞出口工作门开度大于45cm后,挑流冲毁主河槽对岸防洪堤约40m,该防洪堤距挑流鼻坎约70m,冲毁农田及林地约20亩。这一现象这与设计预估偏差较大,这就需要对泄洪发电洞水流在下泄过程中的流动特性以及水体的受力特性等方面进行详细分析,在此基础上进一步探究挑距产生较大偏差的原因。
2 泄洪发电洞结构
泄洪发电洞进水口位于坝轴线上游左岸。由进口段、洞身段、出口控制闸、急流槽和挑流消能段组成。挑流消能段长9.097m,净宽8m,反弧半径20m,挑射角25°,挑流鼻坎高程1054.14m;泄洪洞总长度684.5m;泄洪发电洞进口底高程1068.50m;出口底高程1055.00m(见图1)。当库水位不超过防洪高水位1135.26m时,该洞限泄流量100.0m3/s;库水位达到及超过防洪高水位1135.26m时,闸门全开,隧洞敞泄。
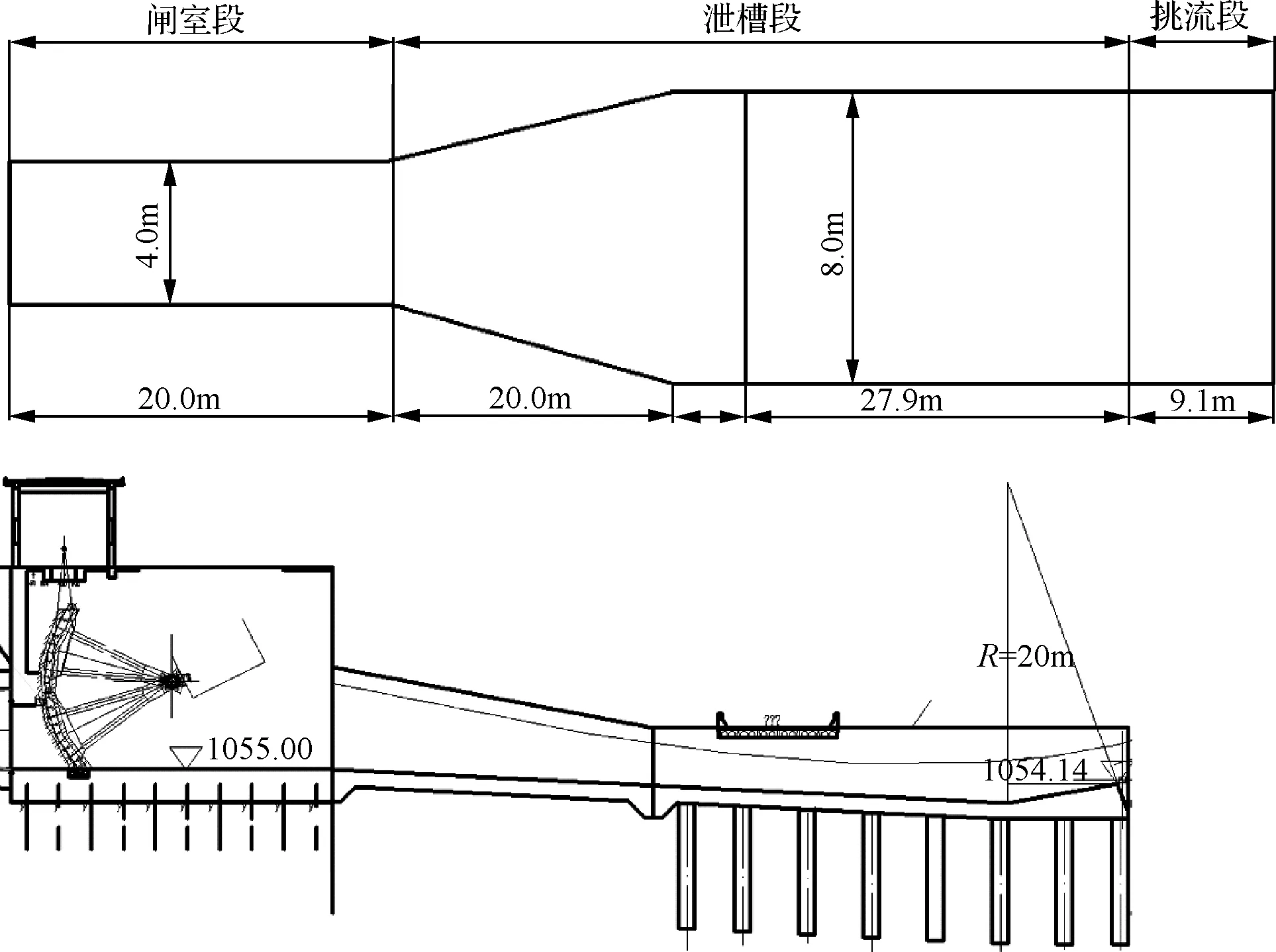
图1 泄洪发电洞出口段布置
3 泄洪发电洞出口挑流消能复核计算
3.1 挑距偏差的原因分析
根据泄洪发电洞运行原理,水流经弧形闸门流出后,流速较大,大量空气自水面掺入水中,以气泡形式随水流运动,形成自掺气水流,水流掺气后对水力特性有较大影响[1-2];水流横断面宽度存在显著变化,而后经挑流反弧段射出。基于此,从泄洪发电洞衔接段水流的流动特性以及挑坎处水流的受力分析等方面对其挑流消能特性进行分析,以揭示挑距出现计算偏差的机理及原因。
3.1.1 糙率n的敏感性分析
由于隧洞的糙率受混凝土材料、施工工艺和运行状态的影响,泄洪洞的实际糙率具有较大的不确定性。为了分析糙率对泄洪洞泄流能力和挑距的影响,这里在泄洪发电洞糙率取值允许范围内,采用不同糙率值对正常蓄水位不同闸门开度下的流量、流速和挑距进行计算。
当库水位达到及超过防洪高水位时,闸门全开,隧洞敞泄。闸门全开时通过泄洪发电隧洞的流量可由下式计算[1]:
(1)
式中μ1——有压隧洞的流量系数;
H0——进口全水头;
hp——出口断面的势能,约等于出口洞高;
A——隧洞出口断面面积;
g——重力加速度,取9.81m/s2。
流量系数按下式计算:
(2)
式中ζi——局部损失系数;
Ai——第i段的计算面积;
A——隧洞出口断面面积;
li——第i段隧洞的长度;
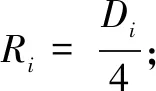
Di——第i段的隧洞直径;
Ci——第i段的谢才系数,常用曼宁公式计算。
曼宁公式如下:
(3)
式中n——糙率。
当库水位不超过防洪高水位时,该洞限泄流量100m3/s;因此需根据不同水位来调节闸门开度,以实现对下泄流量的控制。当闸门局部开启时有压隧洞过流能力的计算公式如下[1]:
(4)
式中H——从收缩断面底部算起的上游水头;
b——闸孔宽度;
e——闸孔开度;
ε2——垂直收缩系数;
μ2——隧洞内闸孔出流的流量系数。
μ2计算公式如下:
(5)
式中Ac——闸后收缩断面面积,Ac=bε2e;
ζg——隧洞内闸门的局部水头损失系数;
A0——闸前断面的隧洞高度;
其余各项的物理意义与闸门全开时相同。
对于弧形闸门,垂直收缩系数ε2主要与闸门相对开度e/H及闸门开度夹角θ有关,θ可用下式计算[2]:
(6)
式中c——弧形闸门转轴高度;
R——弧形闸门半径。
ε2可用下式计算:
ε2=2.11θ-0.276
(7)
依据《溢洪道设计规范》(SL 253—2000),挑流水舌外缘挑距按下式计算:
(8)
式中L——自挑流鼻坎末端算起至下游河床床面的挑流水舌外缘挑距;
h1——挑流鼻坎末端法向水深;
v1——鼻坎坎顶水面流速,按鼻坎处平均流速v的1.1倍计算;
θ——挑流水舌水面出射角,近似取鼻坎挑角;
h2——鼻坎顶点至下游河床高程差;
g——重力加速度,g=9.81m2/s。
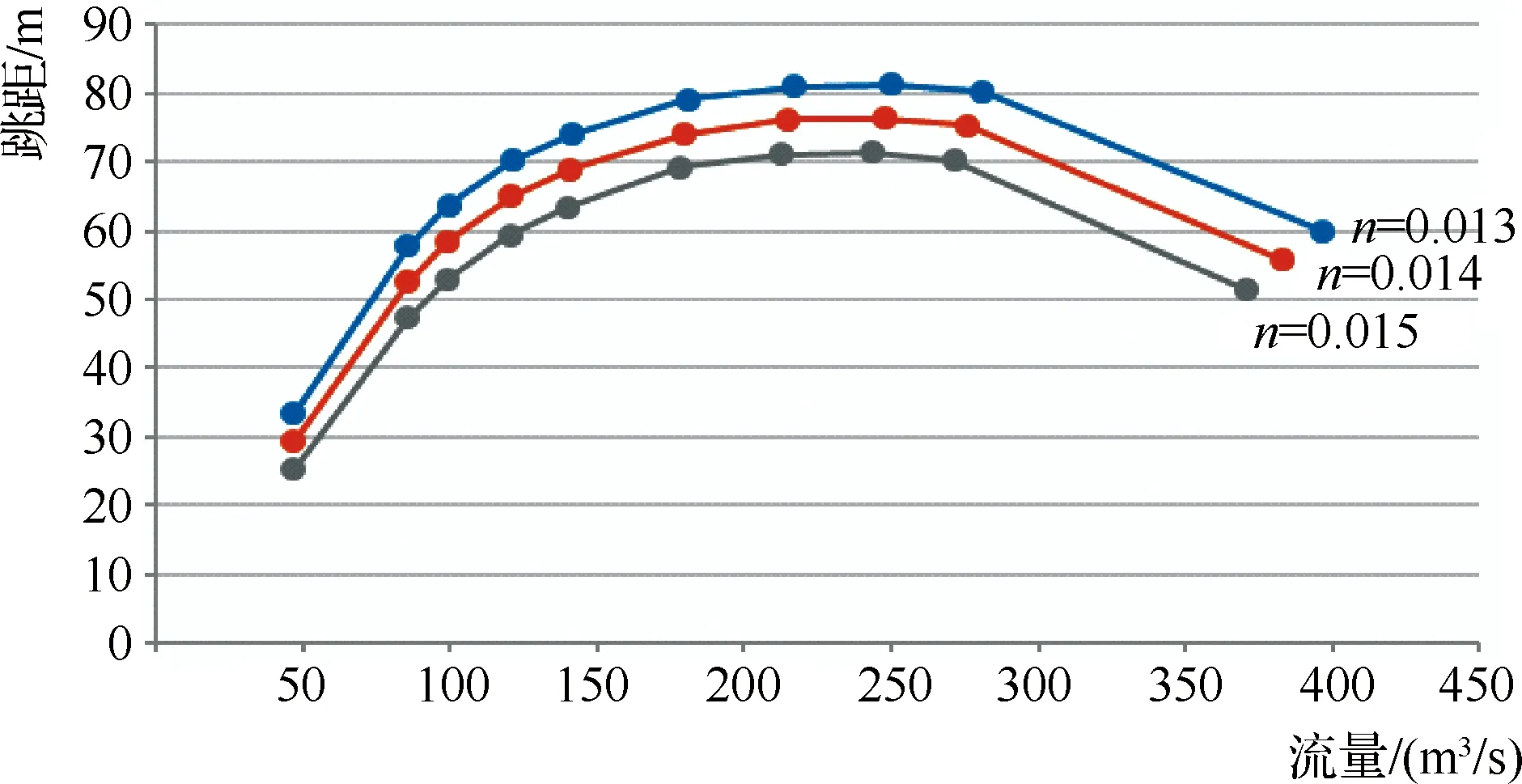
图2 流量及挑距对比
通过对图2进行对比分析,可知糙率对泄洪发电洞泄量影响不显著,但对挑距产生较大影响。
3.1.2 掺气对水流流速的影响分析
为了分析水流自掺气对流速的影响,以正常蓄水位下不同闸门开度工况为例,对掺气稳定后的水流断面位置及断面平均流速进行计算分析(见表1),并给出掺气稳定断面掺气前后各流量对应的流速(见图3)。这里糙率n取0.014。由表1和图3可知:
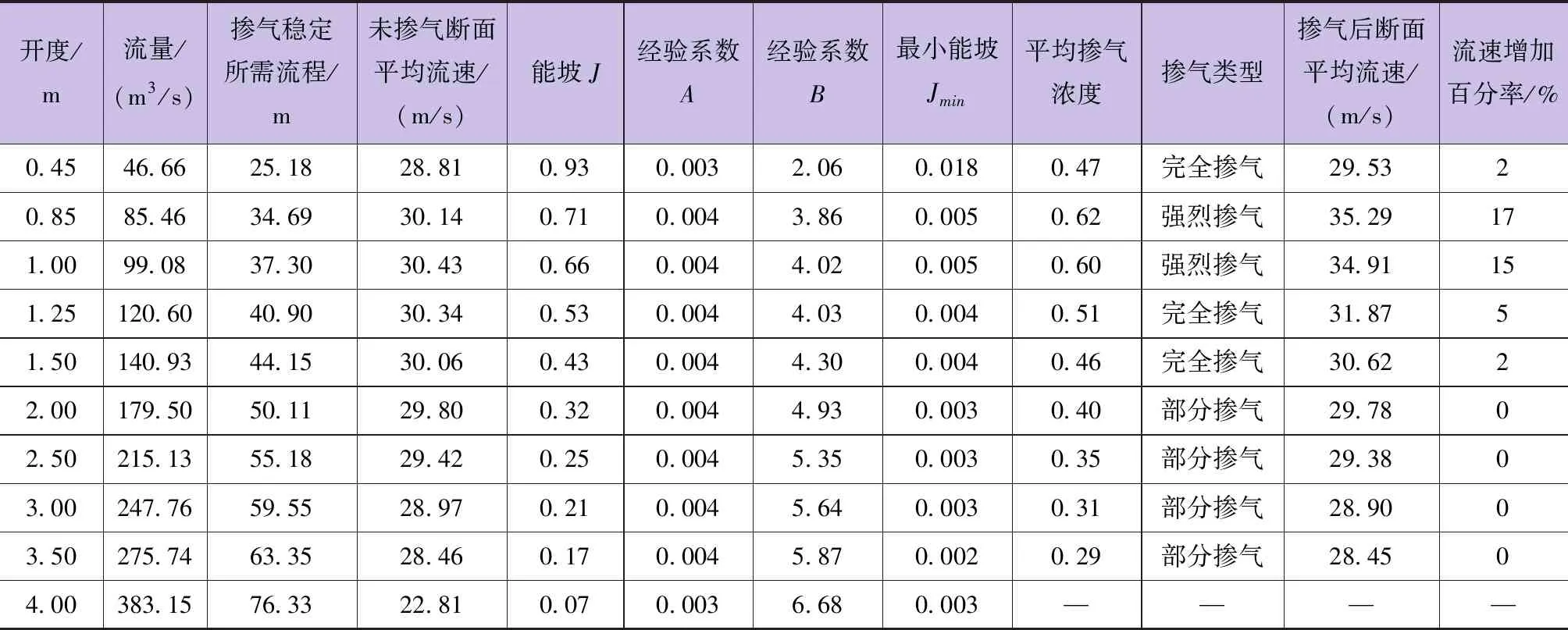
表1 掺气稳定水流断面位置及断面平均流速结果
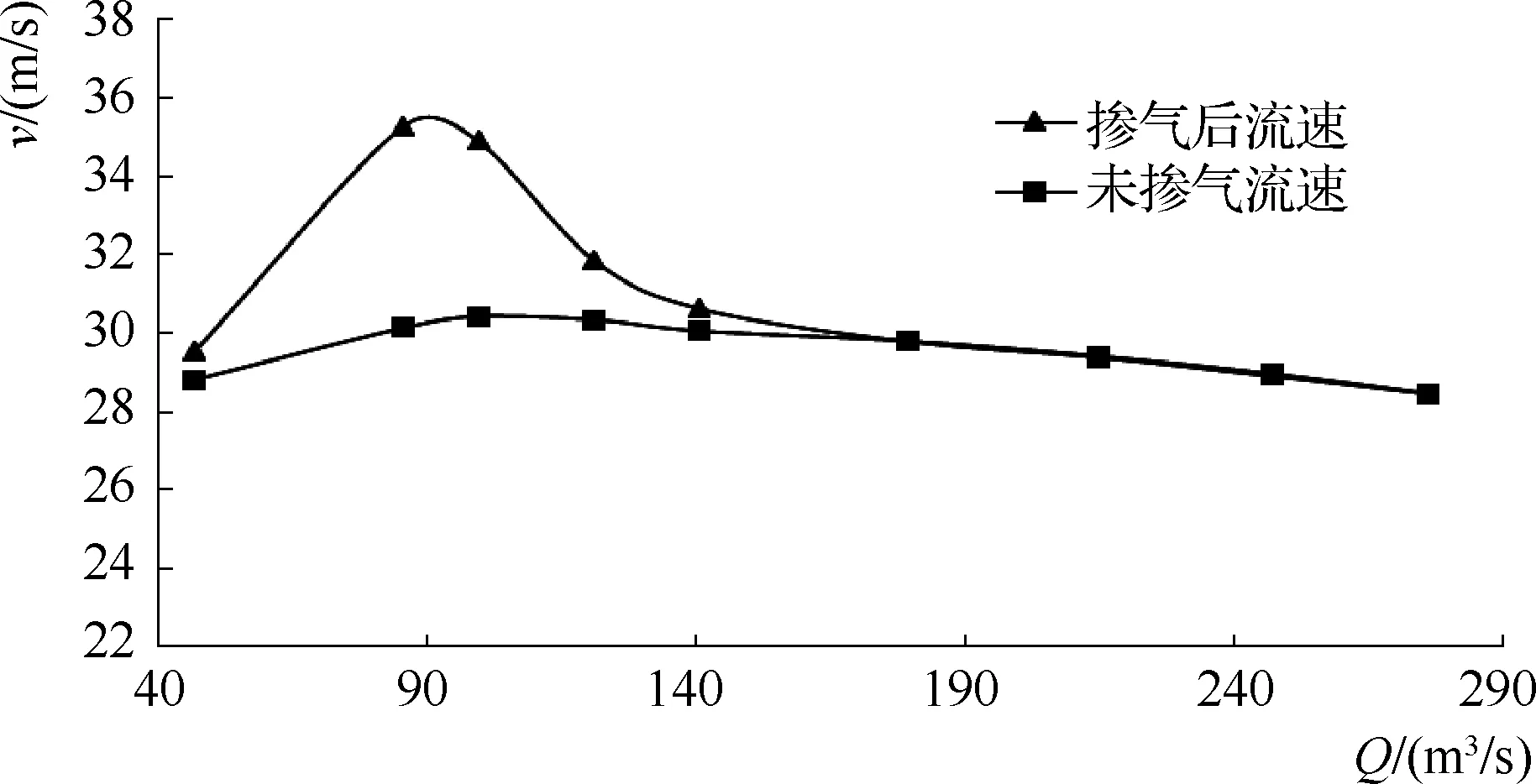
图3 掺气前后流速变化
a.当掺气类型为强烈掺气和完全掺气时,气泡进入剪切层,气泡达到固壁边界层内后,由于掺气的减阻(切应力减小)作用[3-5],固壁对水流的沿程阻力将随着掺气浓度的增加而逐渐减小,掺气水流的断面平均流速将有所增加,故断面平均流速大于相应的非掺气水流的断面平均流速。
b.闸门开度为0.85~1.00m时,全断面强烈掺气,掺气后断面平均流速约为未掺气断面平均流速的1.15~1.17倍,与王才欢等[1]得到的结论基本一致,掺气减阻效应非常显著。
c.由图3可知掺气对流速的影响程度先随着流量的增大而增大,当达到峰值后,随着流量的增大而减小。当泄洪发电洞泄流量在85~100m3/s范围内时,掺气对流速的减阻增速效应最显著。
依据文献[8],当J>Jmin水流即开始掺气。
(9)
(10)
式中J——不掺气水流的水力坡度;
v'——断面平均流速;
n——粗糙率;
R——水力半径;
σ——水的表面张力系数;
γ——水的重度;
θ——渠道底坡角度。
A、B为经验系数,可按下式计算:
A=(3.1+4.26J-4.78J2)×10-3
(11)
(12)
掺气水流的断面平均流速用下式计算:
vaw=(qa+qw)/haw
(13)
式中qa——单宽气体流量;
qw——单宽水体流量;
haw——掺气水流水深。
haw按下式计算:
(14)
式中h——不掺气水流的水深。
根据断面平均掺气浓度的定义:
(15)
式中qa——单宽气体流量;
qw——单宽水体流量。
明渠自掺气水流的掺气浓度分布曲线可用以下公式计算:
水点跃移区
(16)
气泡悬移区
(17)
式中Ca——水点跃移区与气泡悬移区的交界面处的掺气浓度;
hT——交界面至槽底的距离;
σ1——水点扩散高度的标准差;
σ2∞——无限域情况下气泡向下扩散深度的标准差;
σ3——气泡向上反射高度的标准差;
ξ——槽底影响对交界面处掺气浓度的修正系数;
Φ——正态分布函数。
CT与hT可按以下公式计算:
(18)
(19)
σ1、σ3、σ2∞和ξ可通过联立式(12)~式(15)求解得到
(20)
(21)
(22)
(23)
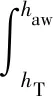
(24)
由式(16)代入式(7)可算得单宽气体流量qa,再由式(5),可得断面平均流速vaw。
王宏硕[9]对溢流表孔泄槽水流表面自掺气始发点位置和全断面掺气位置进行过统计分析,得出了相关经验公式:
S1=10q2/3
(25)
S2=15q2/3
(26)
式中S1——溢流表孔坝顶前缘至泄槽水流表面开始掺气的流程;
S2——溢流表孔坝顶前缘至水流全断面掺气的流程;
q——泄槽单宽流量。
式中S1代表溢流堰顶前的水流由层流发展到泄槽全断面为紊流的流程。而该工程泄洪洞内水流已处于完全紊动状态,当水流从闸门孔口射出时,射流表面即会发生掺气。因此,在有压隧洞水流充分紊动条件下,闸孔后发生水流全断面自掺气的流程S就可以定义为
S=5q2/3
(27)
通过对掺气水流断面平均流速的计算分析可知,水流掺气后,流速分布发生较大的变化,因而在计算鼻坎末端断面平均流速时必须考虑掺气对流速的影响。
3.1.3 反弧段离心惯性力的作用分析
泄水建筑物反弧段水流具有自由水面,同时又受到显著曲率的弯曲壁面影响,反弧段水流的流速分布除受重力影响外,还受离心力的作用。特别是随着泄水建筑物作用水头的增高,反弧段水流流速增大,形成十分复杂的水流现象,这就使得离心惯性力的作用更加显著[6-7]。这里借鉴李建中等[7]的方法对离心惯性力对挑流反弧段流速的影响进行分析。
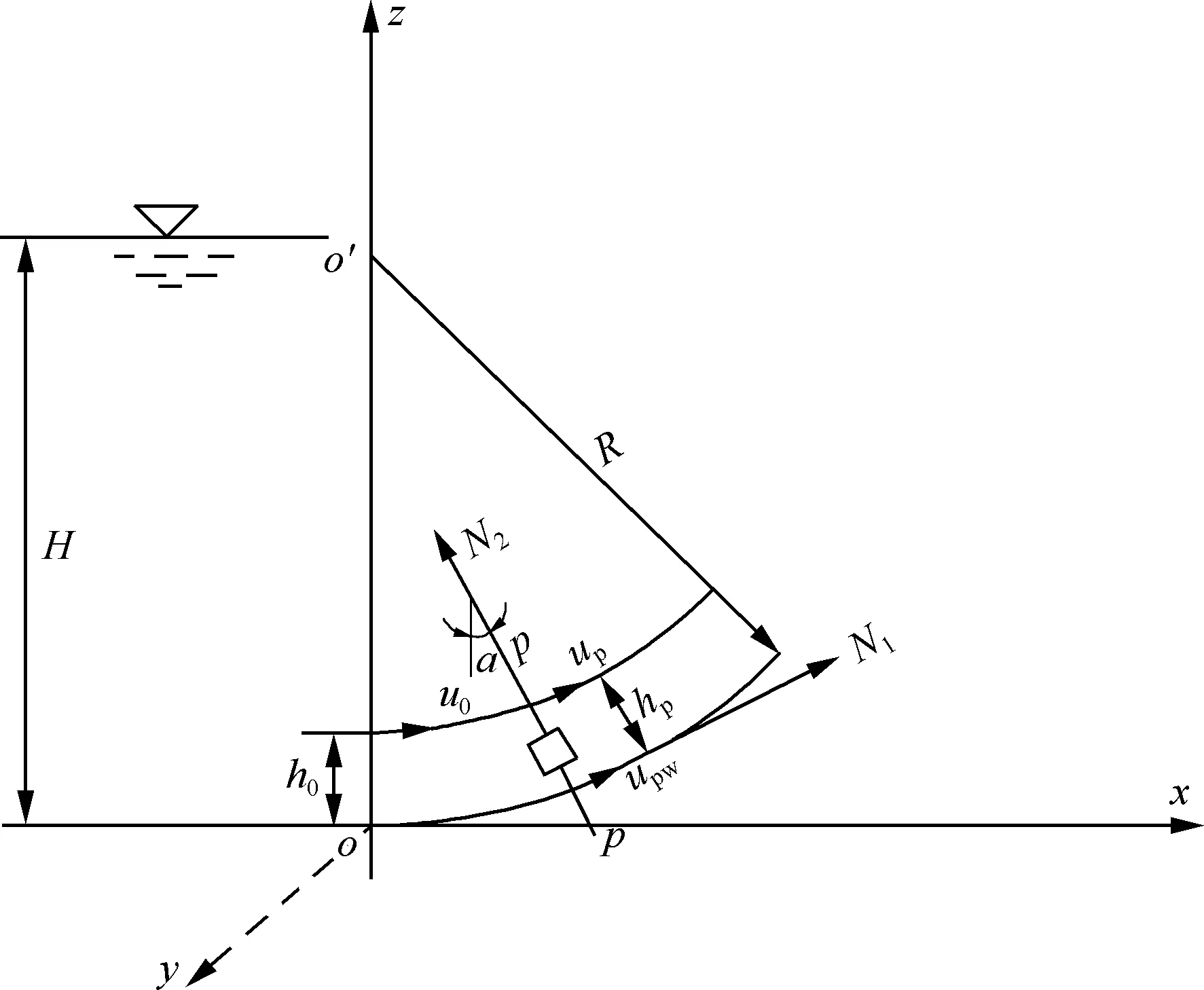
图4 反弧段离心惯性力示意图
在反弧段,由于重力与离心力共同作用,势流速度沿曲面方向(即N1方向)和垂直于曲面的方向(即N2方向)都有变化,见图4,若采用正交曲线坐标系,法向方向为N2,切向为N1,在反弧段势流区任取距壁面为n2、长度为dn2、流动方向为dn1的一微元体,则根据该微元体沿N2方向的动力平衡方程:
(28)
式中up——势流流速;
p——压强;
γ——水的重度;
g——重力加速度;
r——流线的曲率半径。
及势流的伯努利方程:
(29)
就可以得到反弧段势流流速分布的微分方程:
∂up/∂n2=up/r
(30)
代入流线曲率的同心圆假定r=R-n2,积分上式,并根据相应的边界条件确定积分常数后,可得
(31)
式中upw——壁面势流流速。
当n2/R≪1时,上式可以化简为
up=upw(1+n2/R)
(32)
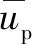
(33)
选用反弧段最低点为基准点,则对反弧水流中任一点均有
(34)
(35)
对动力平衡方程沿水深方向积分可得
(36)
式中pw——壁面势流压强;
hp——截面p-p水深。
根据连续性方程,对反弧水流中任一截面p-p均有
(37)
式中b——反弧段宽度。
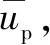
水库在正常蓄水位运行时,不同闸门开度的情况下挑流鼻坎末端断面平均流速的计算结果见表2(粗糙率n取0.014)。
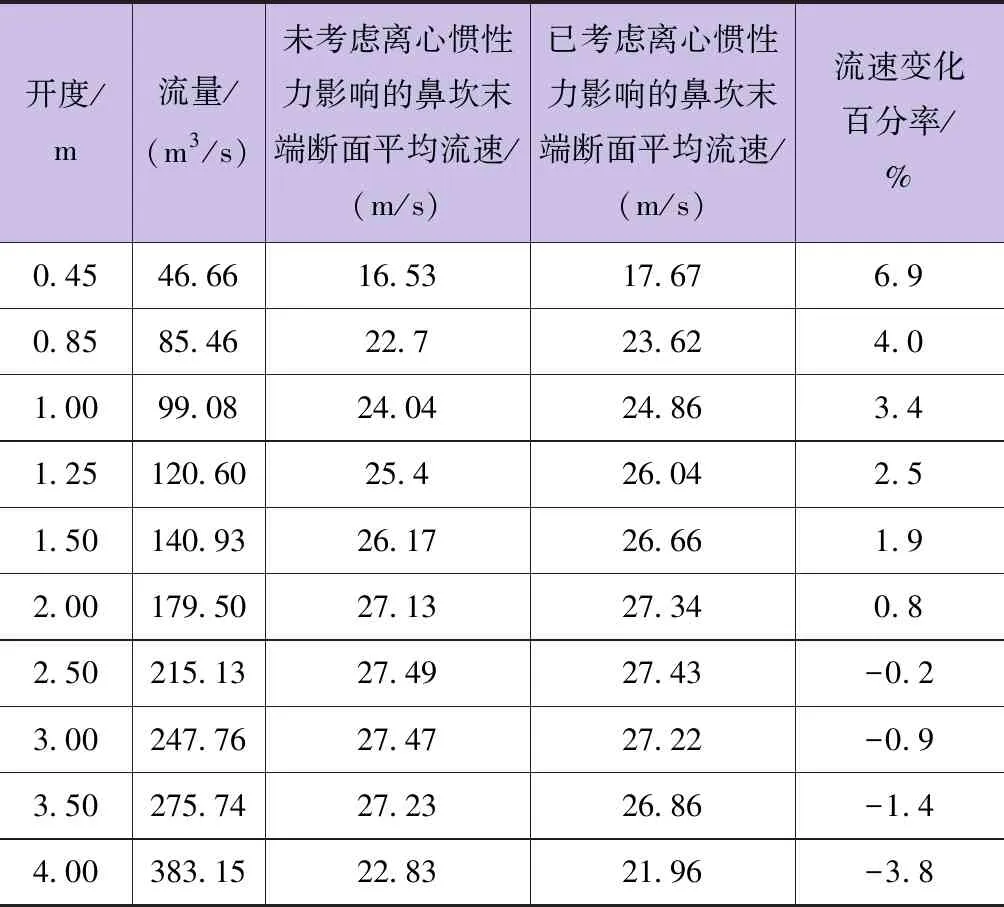
表2 挑流鼻坎末端断面平均流速计算值
由表2可知,在计算过程中,当闸门开度较小时,离心惯性力对鼻坎末端流速的增速作用不可忽视。同时,基于安全考虑,在后文计算过程中,对于大开度情况,不考虑离心惯性力的影响;也就是说当闸门开度大于2.5m后,计算鼻坎末端的断面平均流速时不考虑离心惯性力的作用。
3.2 挑流消能水力参数的验证
为验证计算方法与参数选取的合理性和可行性,这里对泄洪发电洞的泄量和挑距进行计算,并将其与实测资料进行对比分析。本文采用闸门局部开启时有压隧洞过流能力的计算公式对通过泄洪发电洞的泄量进行计算;而后在综合考虑掺气和离心惯性力作用的基础上,对挑流射程进行计算。依式(4)~式(8)计算得表3结果。
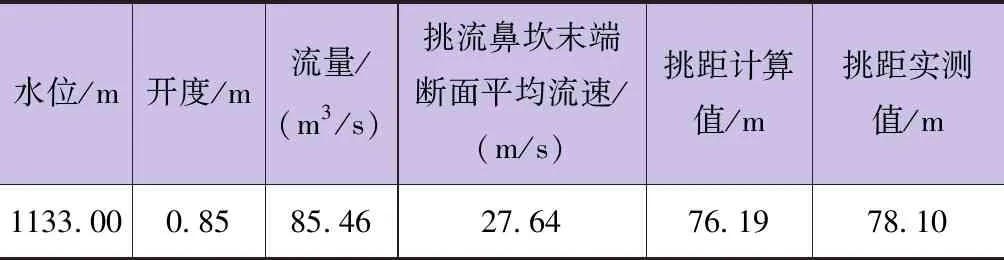
表3 挑流消能计算值与实测值的对比
由表3可见,当库水位为正常蓄水位、闸门开度为0.85m时,泄洪发电洞的泄流量为85.46m3/s,挑距的理论计算值为76.19m,管理局实测挑距为78.10m,二者相差不大。因此可以认为,本文中采用的计算方法和计算参数是基本合理可行的。
综上所述,采用本文的水力参数和计算方法对不同库水位及闸门开度下的挑流消能特性进行计算是基本可行的。
4 计算结果分析
按水库正常蓄水位和设计洪水状况分别进行考虑,对挑流远端影响线距挑流鼻坎的距离进行预测。针对不同的开度,计算出挑距、冲坑深度和挑流远端影响线的位置,结果见表4和表5。
依据《溢洪道设计规范》(SL 253—2000)附录A.3.1之规定,泄槽水面线应根据能量方程采用分段求和法计算。计算基本公式为:
(38)
(39)
式中 Δl1-2——分段长度;
h1、h2——分段始、末断面水深;
v1、v2——分段始、末断面的平均流速;
a1、a2——流速分布不均匀系数,取1.05;
θ——泄槽底坡角度;
i——泄槽底坡,i=tanθ;

n——泄槽槽身糙率系数;


水流经挑流鼻坎挑入空中后,在湍动和空气阻力的作用下,发生掺气及分散,能量部分消散,而其余大部分能量则在水舌落入下游后,在与下游水体的碰撞过程中被消耗。水舌跌入下游河道时,下游河道中的水体相当于一个垫层,与下跌水舌发生碰撞,在入水点附近形成两个巨大的旋滚,主流与旋滚之间发生强烈的动量交换及剪切作用;潜入河底的主流冲刷河床形成冲刷坑。当水舌的冲刷能力与河床的抗冲能力达到平衡时,冲刷坑逐渐趋于稳定,但由于影响因素的多样性和地址条件的复杂性,目前对冲刷坑的发生、发展及其力学特性等影响因素的研究还不充分。因此,工程上常依据一些经验公式来估算冲刷坑的深度,使用不同的冲坑深度计算公式,所得到的冲坑深度计算值也不同,其中公式(40)所得到的冲坑深度值最大,且公式(40)也是规范推荐公式,因此,从建筑物的安全角度出发,本文选用公式(40)来计算挑流消能所造成的冲刷坑深度。
依据《溢洪道设计规范》(SL 253—2000),冲刷坑最大水垫深度可按下式计算:
T1=Kq0.5Z0.25
(40)
式中T——自下游水面至坑底最大水垫深度;
q——鼻坎末端断面单宽流量;
Z——上、下游水位差;
K——综合冲刷系数,依据地质状况,取K=1.1计算。
挑流远端影响线距挑流鼻坎距离计算值(挑流远端影响线位置)=挑距计算值+冲坑深度计算值×河床边坡稳定系数(与原设计相同,取2.5)。
由表4和表5可知,当泄洪发电洞泄量约为100m3/s时,挑距最远;当闸门全开敞泄洪水时,冲坑最深。当水库在正常蓄水位下运行时,泄洪发电洞挑流远端影响线计算值均小于原设计的防洪堤内护角边线距挑流鼻坎的距离;当水库在设计洪水位下运行,闸门开度为3.50m时,泄洪发电洞挑流远端影响线计算值超出原设计值。
5 结 论
通过对泄洪发电洞下泄水流行进过程中的流态、受力情况、紊动掺气特性等进行分析,可知挑距产生偏差的原因主要是水流的掺气减阻效应和离心惯性力的影响。分析发现,掺气减阻效应对挑坎末端断面平均流速的影响最为显著,流速最大可增大17%;当闸门开度较小时,离心惯性力的作用对挑坎末端断面平均流速的增速作用较明显,在0.8%~6.9%之间。规范中挑流消能公式没有考虑掺气和离心惯性力的作用,因此,造成挑距计算值与实测值之间存在较大偏差。对正常蓄水位和设计洪水位下不同闸门开度运行时的挑流消能特性计算结果表明:当泄洪发电洞泄量约为100m3/s时挑距最远,约85m;当闸门全开洪水敞泄时冲坑最深,约23m;当水库在正常蓄水位下运行时,挑流远端影响线计算值均小于原设计的防洪堤内护角边线距挑流鼻坎的距离;当水库在设计洪水位下运行,闸门开度为3.50m时,挑流远端影响线计算值超出原设计值。
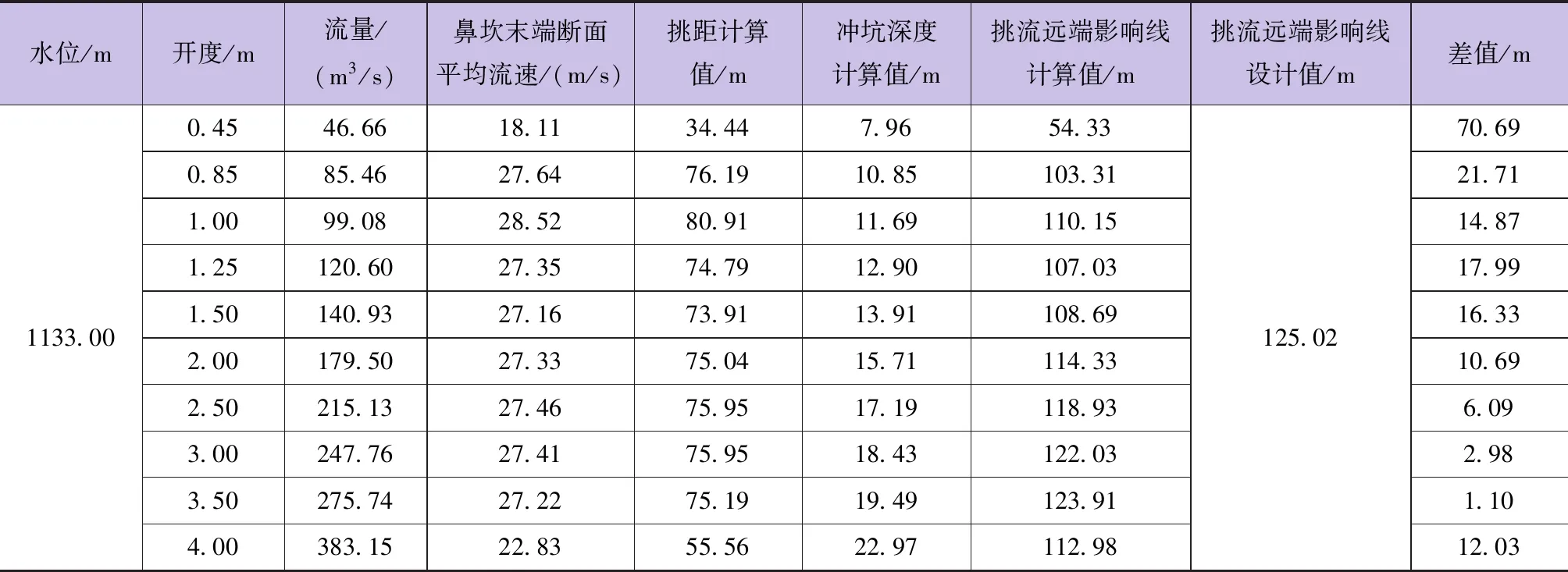
表4 正常蓄水位下泄洪发电洞出口挑流消能计算
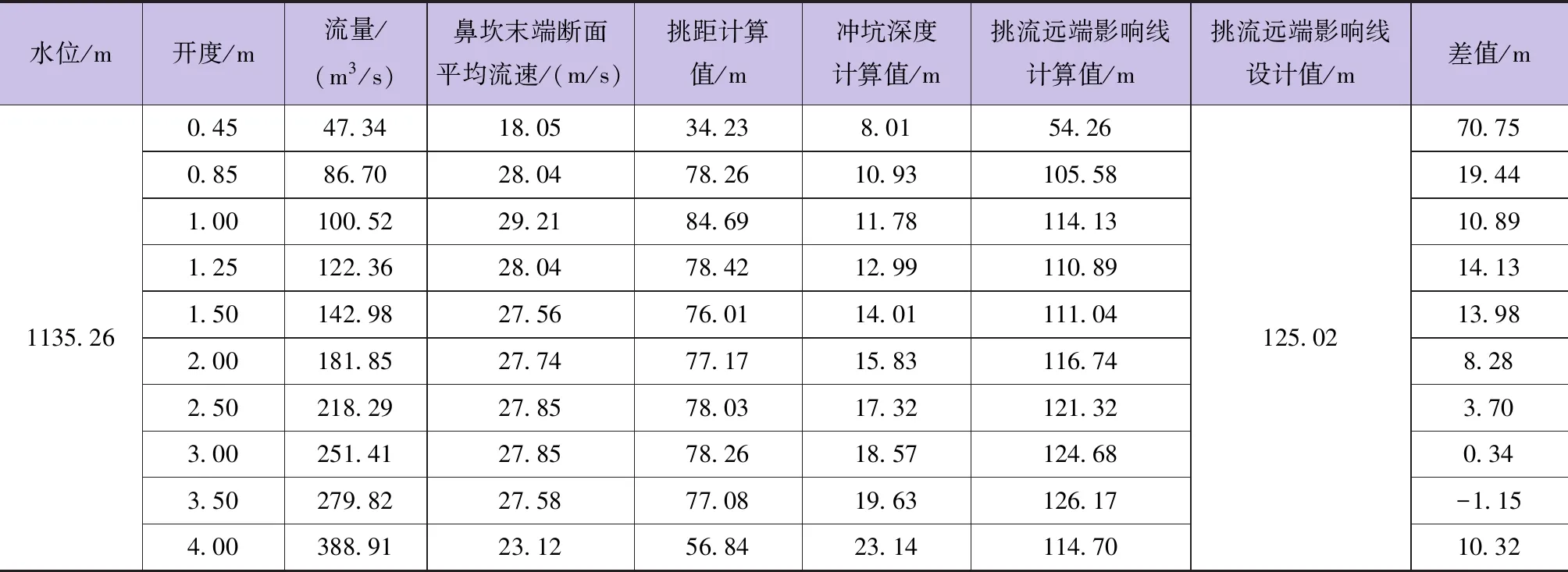
表5 设计洪水位下泄洪发电洞出口挑流消能计算
