基于Copula函数的雷州半岛气象干旱风险分析

张得胜，江涛，黎坤，蒋可元，单云龙

(1.水利部珠江水利委员会珠江水利综合技术中心，广东广州510611； 2. 中山大学地理科学与规划学院，广东广州510275；3.水利部珠江水利委员会技术咨询中心，广东广州510611)

受全球气候变化影响，极端干旱事件频繁发生，干旱以其发生频次高、波及范围广、持续时间长等特点，易对人类生产生活以及社会经济发展产生危害，是现今社会普遍关注的热点问题之一[1]。根据不同研究角度和旱情影响范围，可以将干旱分为气象干旱、农业干旱、水文干旱以及社会经济干旱四大类[2]，其中气象干旱是其他干旱类型的基础，对气象干旱加以研究是摸清和预判其他干旱类型的前提[3]。目前国内外采用诸如标准化降水指数(SPI)[4-5]、标准化降水蒸散发指数(SPEI)[6-7]以及帕默尔干旱指数(PDSI)[8-9]等方法对气象干旱的发生情况(或特征)等进行统计研究。其中SPI是国际上推荐使用的一种气象干旱指数，其计算简单，计算资料容易获取但只考虑降雨因素[10]，SPI不受温度、蒸散发、风速及土壤持水能力等因素的影响，在干旱研究领域得到了广泛的应用[11-13]。

雷州半岛位于中国低纬度地区，受季风气候的影响，降雨时空分布不均且旱季较长，是广东省干旱灾害较为严重的区域[14-15]。陈子燊等采用旋转经验正交函数(REOF)和小波分析等方法研究了广东省近50 a来干湿时空变化特征，发现以雷州半岛为主的粤西沿海区域有显著的干旱趋势[16]；任启伟等采用标准化降水蒸散发指数(SPEI)识别了广东省干旱发生情况，发现雷州半岛冬春连旱加剧显著[7]。黄晓梅等对雷州半岛干旱的特征及其大气环流进行了分析，研究发现大气环流影响着雷州半岛的季节性干旱的时空分布特征[17]；王壬等基于雷州半岛近30 a的逐日降水资料，采用各种方法分析了雷州半岛季节性气象干旱的时空特征，发现日尺度EDI与SPI6均适用于雷州半岛的干旱监测[18]，上述文献主要针对雷州半岛干旱时空变化特征及成因进行研究，对该地区的干旱风险研究甚少。为此，本文采用旋转经验正交分解将气象干旱空间分布分解成不同的空间模态，对不同模态区域采用Copula函数进行干旱风险分析，以期为区域干旱预警以及风险管理提供科学依据。

1 研究区域概况及资料来源

雷州半岛处于中国大陆最南侧，广东省西南角，位于东经109°31′～110°55′、北纬20°12′～21°35′，东临南海，西濒北部湾，南隔琼州海峡与海南省相望，北部廉江市。半岛属于热带季风气候，年平均气温23℃，年平均降水量1 400～1 700 mm，其年降雨量变差系数Cv值处于0.18～0.28之间，气温较高，日照强度强，致使蒸发量大，年蒸发量均为全省最高，多年平均干旱指数达0.9～1.0，其大部分地区蒸发能力与降水量已十分接近，局部地区蒸发能力大于降水量，使得区域气候偏于干旱，造成水资源严重失衡[19]。雷州半岛河流短小且独流入海，且以松散的火山土质为主，透水性良好，不易存水，一遇晴热无雨时间较长，大部分河流就呈现断流的现象[20]，水资源矛盾突出，因此干旱比较严重。根据雷州半岛雨量站建站分布情况，选取12个雨量测站1966—2015年共计50 a的逐月降雨量数据，数据来源于湛江市水文局。所有测站资料完整，无缺测数据。研究区域范围及雨量站分布情况见图1。

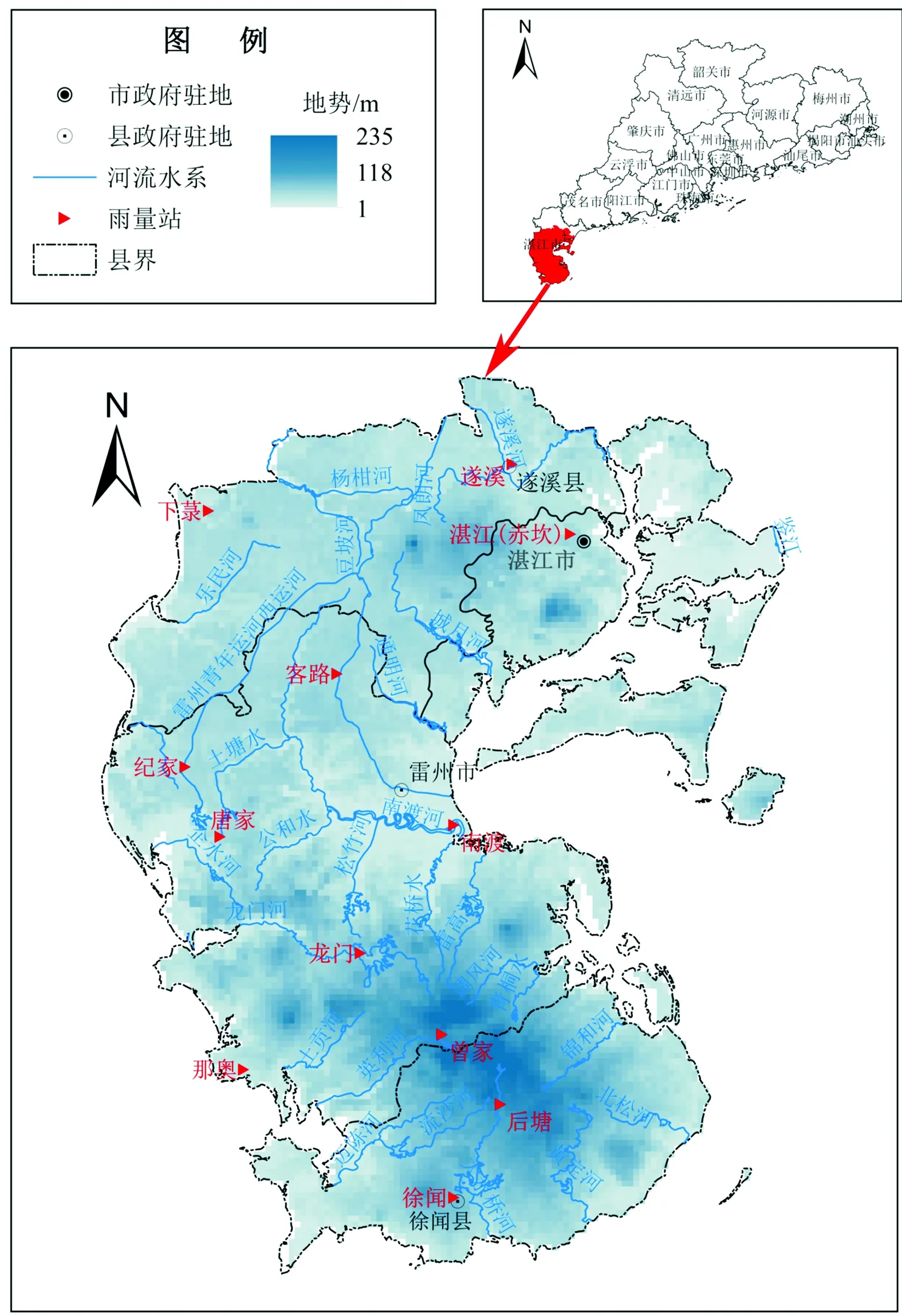
图1 研究区域范围及雨量站分布

2 研究方法

2.1 标准化降水指数(SPI)法

由于标准化降水指数(SPI)法，其计算只考虑降雨数据，并不受温度、蒸散发、风速及土壤持水能力等因素的影响，所以是国际上推荐使用的一种气象干旱指数。SPI能够较好地反映干旱强度和持续时间，使得用同一干旱指标反映不同时间尺度和区域的干旱状况成为可能，因而得到广泛应用。王壬等基于雷州半岛近30 a的逐日降水资料，采用各种方法分析了雷州半岛季节性气象干旱的时空特征，发现日尺度EDI与SPI6均适用于雷州半岛的干旱监测[18]，因此本文选取SPI6进行雷州半岛气象干旱分析。SPI指数计算原理为：计算出某时段降雨量的Γ分布概率值，再进行正态标准化处理，最后采用标准化降水累计频率分布来划分干旱等级，其划分标准见表1。SPI的计算过程详见GB/T 20481—2006《气象干旱等级》[21]。

表1 SPI干旱等级划分标准

2.2 旋转经验正交分解法(REOF)

EOF分解也称经验正交函数分解，最早由统计学家Pearson提出[22]。EOF分解主要应用在气象和海洋资料分析中，其优点是可以用较少的几个新变量序列来反映原多个变量的变化信息，能够起到降低资料维数的作用[23]。计算原理为：先对原始数据做标准化处理，计算协方差矩阵，然后用求实对称矩阵特征值及特征向量的办法，求出协方差矩阵的特征值和特征向量，再将特征值从大到小排列，并求出时间系数矩阵，最后计算每个特征向量的方差贡献及累计方差贡献率。

旋转经验正交分解(REOF)是以经验正交分解(EOF)为基础。首先，EOF对气象要素场进行时空分解，在此基础上采用REOF进行方差最大旋转，提取方差最大的前几个空间模态和相应的时间向量。与单纯的EOF分解相比，REOF分解使得高荷载值集中于较小的区域上，其余大部分区域的荷载值接近于零，空间结构较清晰，有利于对研究要素加以分区。

对于干旱特征变量的选取一般采用游程理论。1967年，Yevjevich[24]最先采用游程理论对干旱事件进行了识别(图2)。根据游程理论，选取系数值-0.5作为截取水平X0，当系数值序列x(i)(i=1,2,3…，N)在一个或多个时段内连续小于X0时，就出现负游程，说明发生了干旱，负游程的长度作为干旱历时，记为D(月)；负游程历时时间段内所有SPI累加值的相反数作为干旱烈度，记为S，干旱事件划分示意见图2，其计算公式如下：

(1)

2.3 Copula函数原理

干旱事件本身具有非线性以及复杂多变性的特点，同一干旱事件的变量不一定服从相同的分布，因此传统的多变量频率分析方法不能更好地描述干旱事件的特性，而Copula函数各变量的边缘分布函数相对自由，可以选择不同类型边缘分布的干旱特征变量构建联合分布模型[23]。目前Copula函数在干旱风险及条件概率研究领域应用十分广泛[26-27]。根据Sklar[28]的理论，假设X和Y为连续随机变量，若u=FX(x,y)和v=FY(x,y)分别为随机变量X和Y的边缘分布函数，FX,Y(x,y)为联合分布函数，那么存在唯一的Copula函数C，使得：

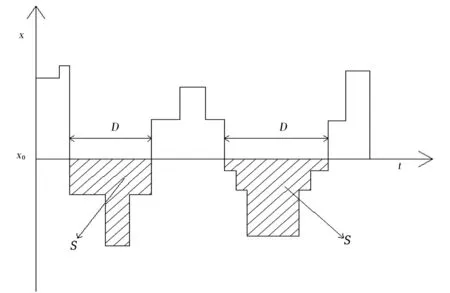
图2 干旱识别游程理论示意

FX,Y(x,y)=Cθ(FX(x),FY(y))=Cθ(u,v)

(2)

式中θ——待定参数。

Copula函数种类较多，根据其交换性，可以将Copula函数分为对称Copula(Symmetric Copula)和非对称Copula(Asymmetric Copula), 其中Archimedean Copula函数是Copula函数中较为常用的一种函数，其基本形式[29]为：

Cθ(u,v)=φ-1[φ(u)+φ(v)]

(3)

式中φ(t)——Copula函数生成元，必满足①φ(1)=0、②φ(0)=∞、③φ'(t)>0、④φ″(t)>0，t⊂(0,1]；φ'(t)、φ″(t)——一阶和二阶导数；φ-1(t)——φ(t)的反函数；u、v——随机变量的累积概率。

采用耿贝尔(Gumbel)分布、三参数广义极值(GEV)分布和威布尔(Weibull)分布来拟合D与S，应用线性矩法估计参数[30]，并采用概率点据相关系数值(PPCC值)最大值所对应的分布作为D与S的边缘分布函数，之后对其所选择的边缘分布函数进行经验点距与理论分布拟合检验，分析所选分布是否最优。

本文主要采用Gumbel-Haugaard(简写为G-H，下同)Copula、Clayton Copula和Frank Copula 3种常见的Archimedean Copula函数，其分布函数及参数计算公式[31]见表2。采用相关性指标法对3种Copula函数参数进行估计：首先，计算D与S之间的Kendall相关系数τ，然后根据τ与θ关系计算3种二维Archimedean Copula函数的参数[32]；其次，计算相应的均方根误差RMSE值和AIC值。根据RMSE准则[33]和AIC准则[34]，其值越小则Copula函数的拟合效果越好；最后，采用Genest-Rivest方法进一步选出拟合效果最佳的Copula函数，具体计算方法见[35]。

表2 3种Copula函数的分布函数及参数计算公式

对于二维干旱变量D与S的联合分布的重现期，包括“或”重现期和“且”重现期。“或”重现期指的是2个变量中，其中一个变量发生时所对应的重现期；“且”重现期是指2个变量同时发生时所对应的重现期。由于干旱历时有可能会超过1 a，在同1 a内也有可能会发生多次干旱事件，因此在其他水文气象频率分析中常用的年最大序列重现期计算原理对于干旱频率分析并不适用[36]。Shiau定义了基于干旱间隔时间的“且”和“或”联合重现期的计算式[37]为：

(4)

(5)

式中TD∩S、TD∪S——“且”和“或”联合重现期；E(L)——干旱间隔期望，为干旱历时与非干旱历时的平均值之和；FD(d)、FS(s)——干旱历时和干旱烈度的边缘分布函数；C(FD(d),FS(s))——Copula函数。

对于两类条件概率，在其中某一变量发生某一非期望事件的条件下，另一变量也发生某一非期望事件的概率，可称为遭遇风险率；而当某一变量未发生非期望事件的条件下，另一变量却发生某一非期望事件的概率，可称为组合风险率。根据联合概率分布，在给定的设计值下，干旱历时与干旱烈度的“或”重现期与“且”重现期风险概率计算公式[37]为：

(6)

(7)

3 结果与讨论

3.1 干旱空间模态分解

采用REOF对不同时间尺度1、3、6、12和24个月的SPI值进行空间模态分解，分解结果显示不同时间尺度得到的空间模态荷载中心相同，王壬等认为SPI6对应的干旱识别结果与实际发生干旱比较接近[18]，因此，本文选取时间尺度6个月的SPI6进行数据研究。采用REOF进行空间模态分解，其方差贡献及累计方差贡献见表3。

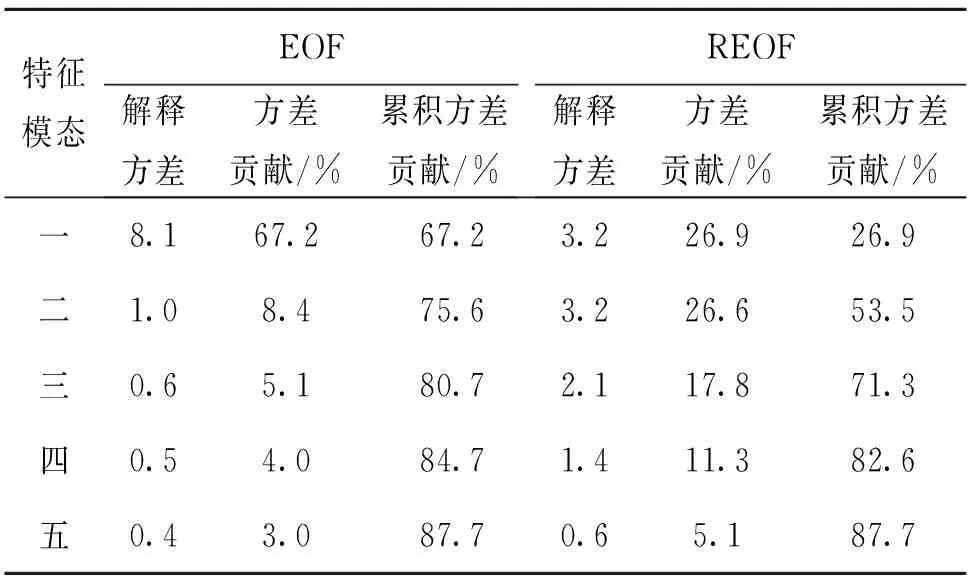
表3 方差贡献及累计方差贡献

由表3可知旋转前第一空间模态达到67.2%，其余空间模态方差贡献率基本小于10%，旋转过后方差贡献率比旋转前更加均匀，其前5个模态累计方差率达到87.7%，不同模态对应不同区域，详见图3。由图3可知：第一空间模态的荷载中心区域位于徐闻大部分区域；第二空间模态的荷载中心位于雷州西部地区；第三空间模态的荷载中心位于湛江市区；第四空间模态的荷载中心位于遂溪西部地区；第五空间模态的荷载中心位于遂溪的东南部及雷州的东北部地区。第一空间模态与第二空间模态的方差贡献率达到53.5%，说明近50 a来徐闻地区和雷州市西部地区是雷州半岛经常出现的较为干旱的地区。查阅历史资料可知，雷州半岛干旱具有南部严重于北部的特点，而徐闻地区历年是最为干旱的地区，本次结果与实际干旱发生情况较为吻合，因此可以很好地反应整个雷州半岛地区干旱的空间分布情况。

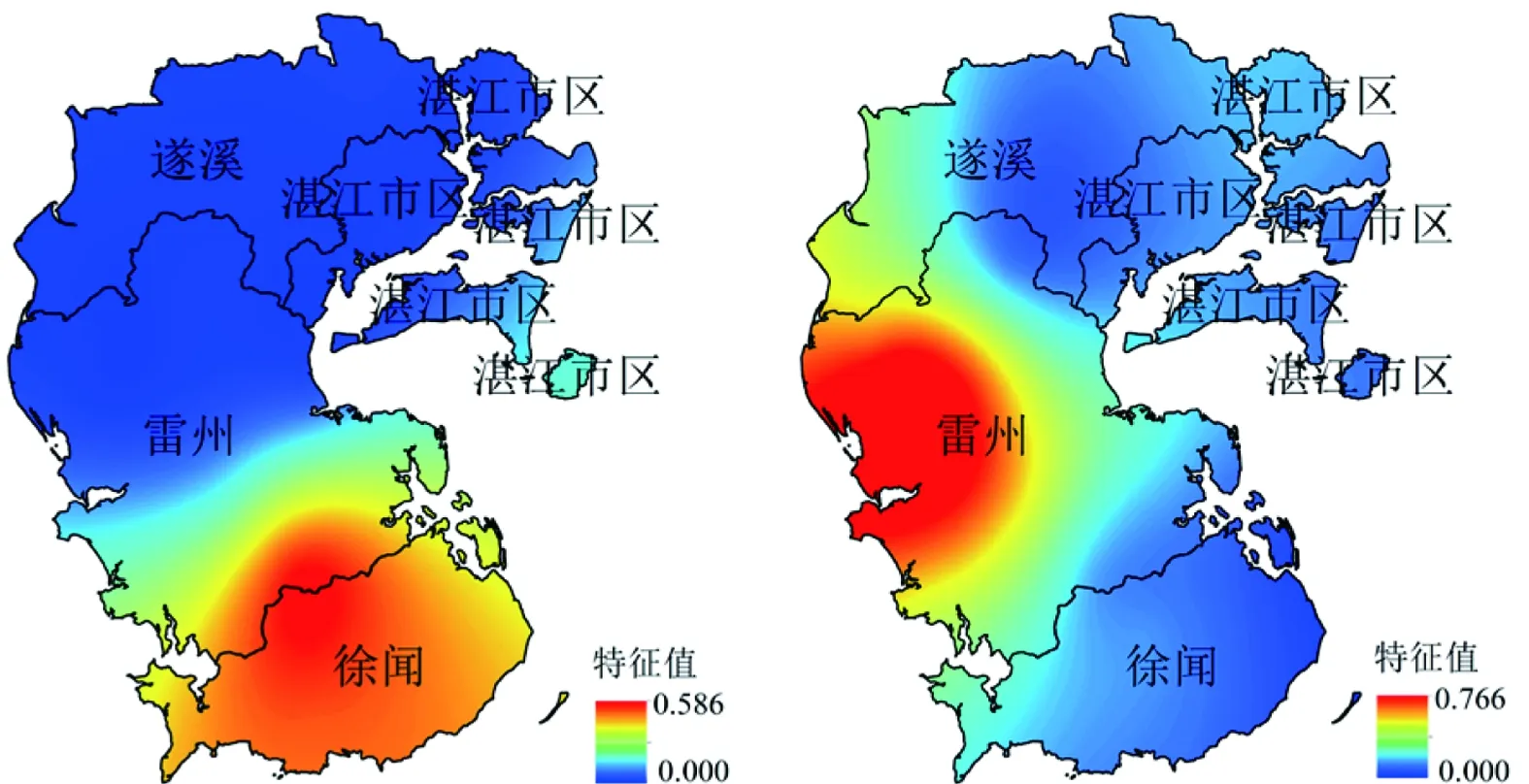
a) 区域一 b) 区域二图3 不同模态区域特征向量分布

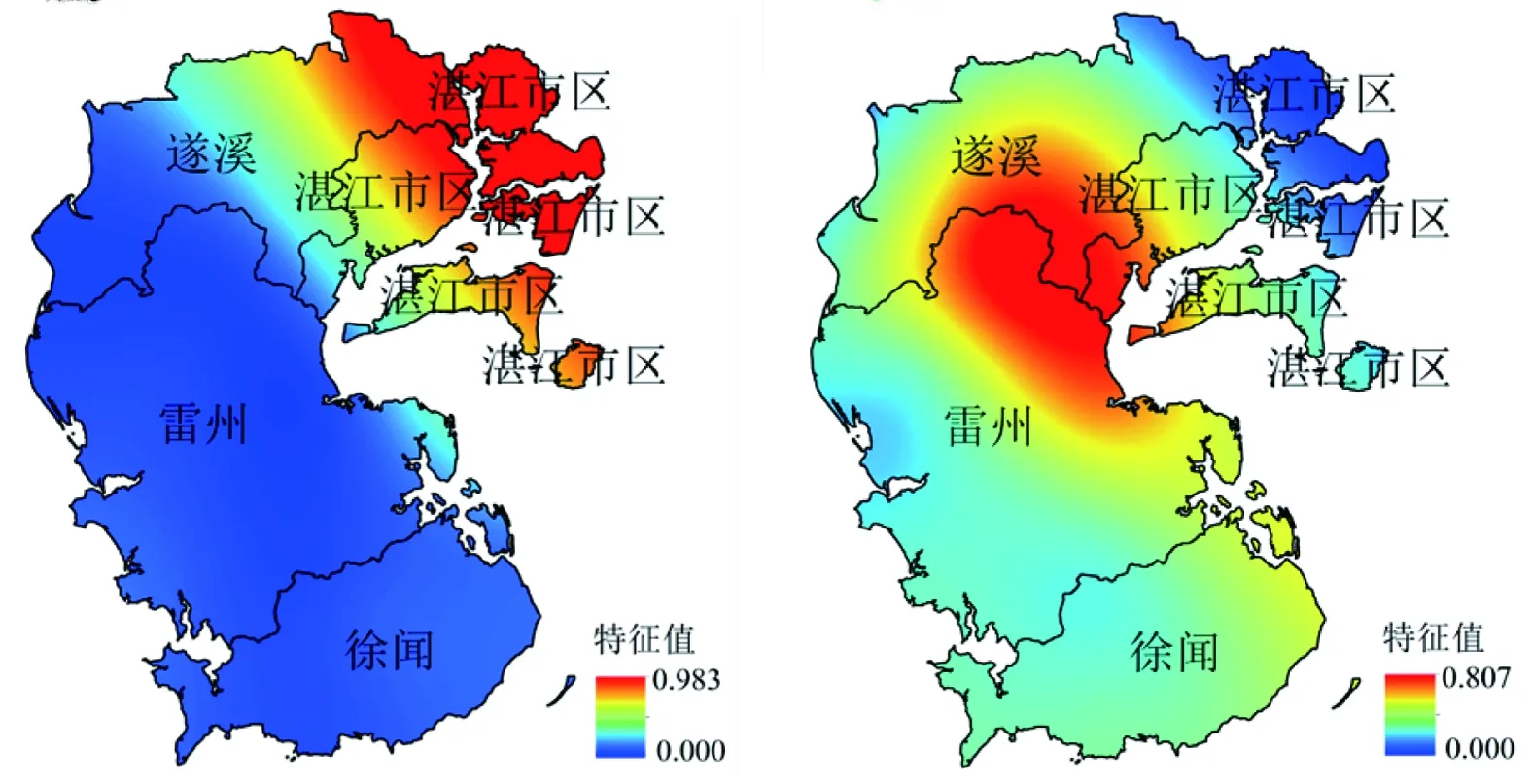
c) 区域三 d) 区域四

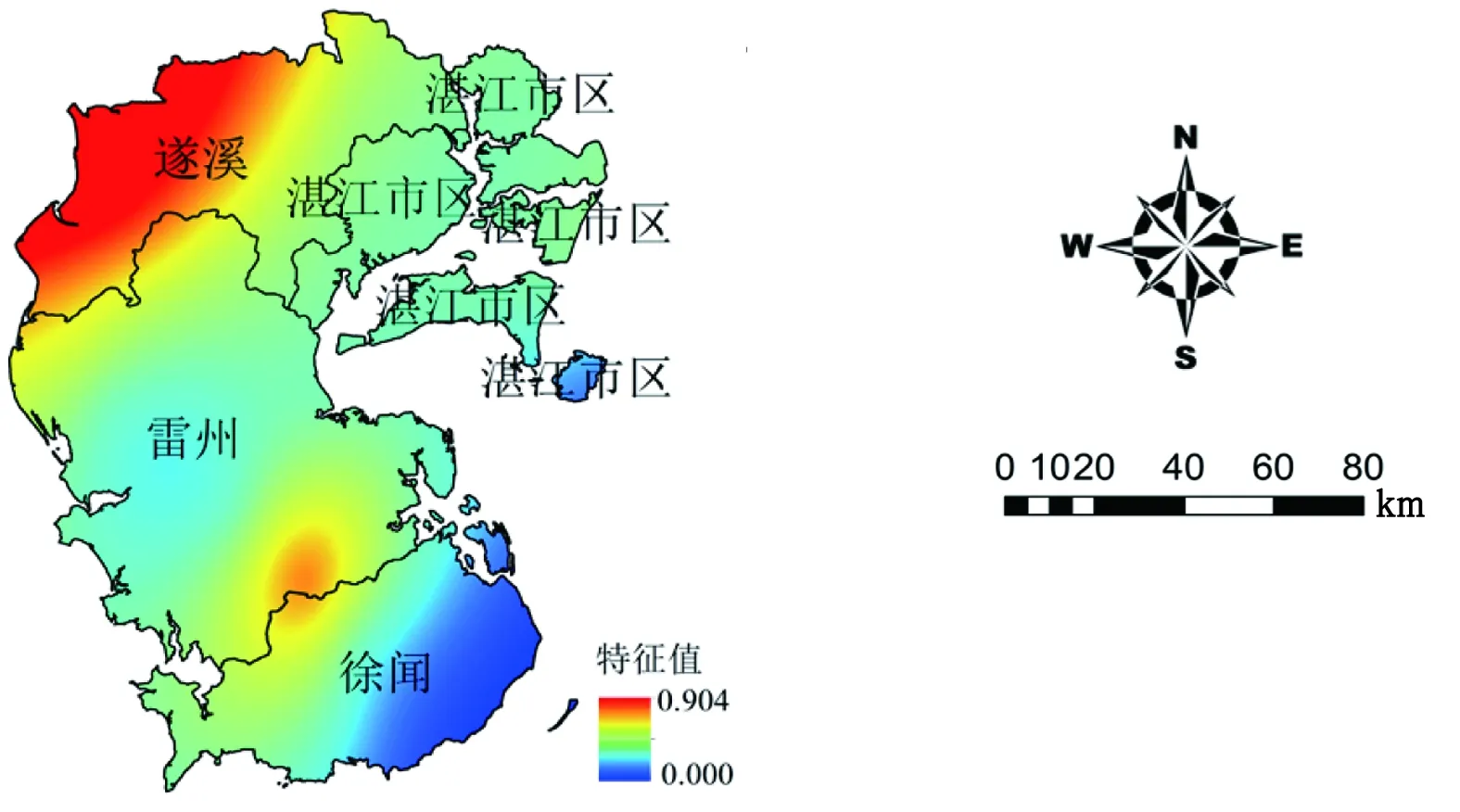
e) 区域五 续图3 不同模态区域特征向量分布

3.2 干旱风险分析

采用耿贝尔(Gumbel)分布、三参数广义极值(GEV)分布和威布尔(Weibull)分布来拟合D与S，其PPCC检验值以及边缘分布参数计算结果见表4。由表4可知，对于PPCC检验来说，其值越大所服从的边缘分布函数最优，因此选取GEV分布作为D与S的边缘分布函数，其经验点距与理论分布拟合检验效果见图4(由于篇幅限制，只列出区域一D与S经验点距与理论分布拟合效果)。由图4可知，D与S的经验点距基本落在理论分布曲线上，边缘分布函数采用广义极值(GEV)分布拟合效果最好。因此选用GEV作为不同模态D与S的边缘分布函数。

采用相关性指标法对G-H Copula、Clayton Copula和Frank Copula函数参数进行估计，其Kendall相关系数τ、Copula函数参数θ值、RMSE值和AIC值见表5。RMSE与AIC值最小时，所对应Copula函数拟合效果最好。由表5可知，3种Copula函数对应的RMSE与AIC值都十分接近，其中G-H Copula 函数对应的RMSE值与AIC值最小，因此G-H Copula 函数可以更好的用来建立D与S的二维联合分布。为了进一步验证G-H Copula 函数的拟合效果最好，采用Genest-Rivest方法对3种二维Archimedean Copula函数进行拟合，拟合结果见图5(由于篇幅限制，只列出区域一拟合效果)。

表4 边缘分布PPCC检验值及参数估计值

注：表中加粗的值对应的函数是最优的分布

a) 区域一D

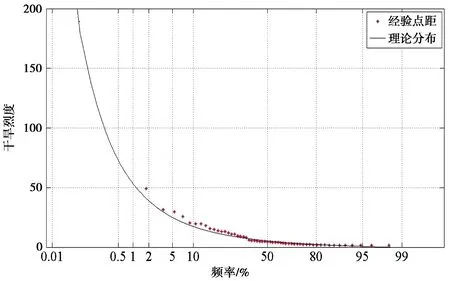
b) 区域一S图4 区域一D与S经验点距与理论分布拟合

区域Kendall相关系数τCopula函数类型θRMSEAIC区域一0.783 2G-H4.612 50.001 67-349.872 7Clayton7.225 10.002 34-331.149 8Frank16.624 60.002 52-326.904 0区域二0.781 2G-H4.570 40.002 48-298.050 2Clayton7.140 80.003 35-282.889 0Frank16.453 90.003 67-278.437 4区域三0.709 6G-H3.443 50.002 77-339.576 3Clayton4.887 10.003 04-334.136 8Frank11.864 50.003 43-327.179 1区域四0.830 9G-H5.913 70.001 12-364.687 3Clayton9.827 30.002 46-322.511 2Frank21.876 00.001 17-362.784 4区域五0.895 5G-H9.569 40.001 76-264.373 0Clayton17.138 80.003 36-237.227 0Frank36.555 10.001 90-261.237 9

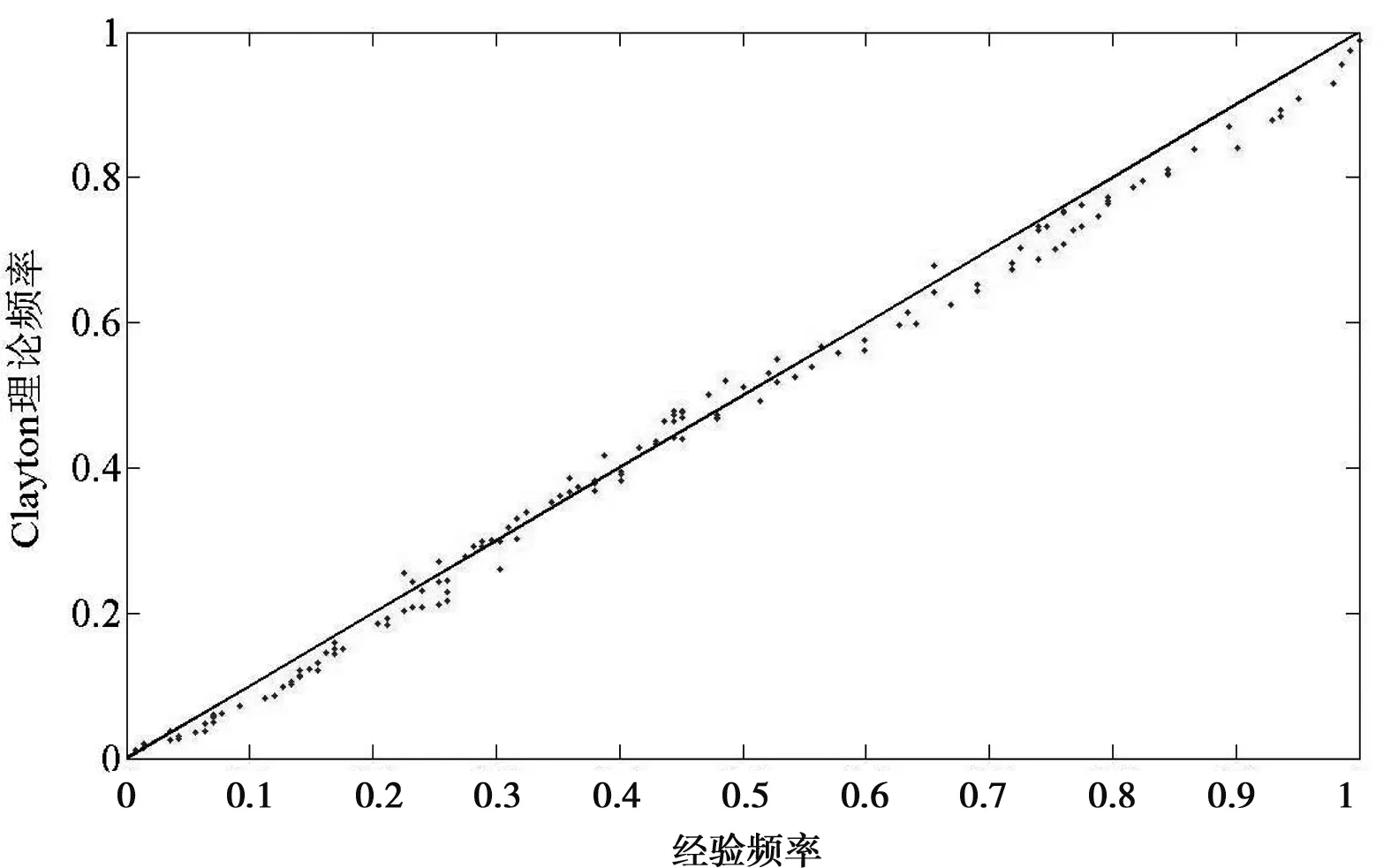
a) Clayton Copula

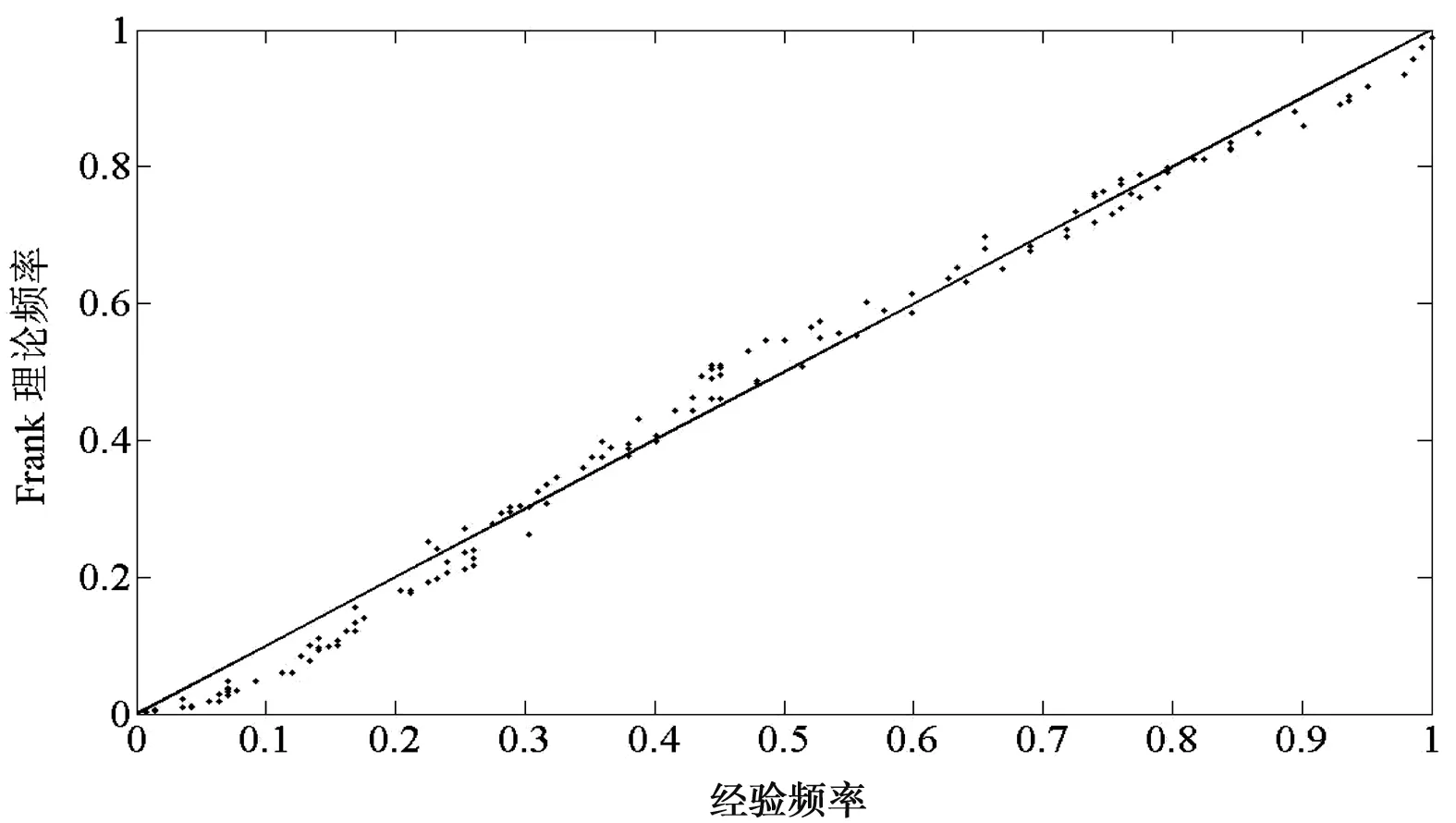
b) Frank Copula

c) G-H Copula图5 D与S联合分布拟合优度对比

式(4)、(5)中E(L)为干旱间隔期望值，基于系数值统计得到的区域一到区域五对应的E(L)值依次为12.39、14.31、10.45、9.08、7.73 a。给定6个重现期(100、50、20、10、5、2 a)，计算得到D与S联合分布的“或”重现期和“且”重现期以及风险率见表6。由表6可知如下结论。

a) 对设定的6个重现期(100、50、20、10、5、2 a)，边缘分布的重现期介于“或”重现期和“且”重现期之间，联合分布的这2种重现期可以看作是边缘分布的2种极端情况。以边缘分布重现期100 a为衡量标准，6个区域D与S联合分布的“或”重现期介于83.1～86.8 a之间，“且”重现期介于117.9～125.6 a之间，可认为，实际重现期所处区间为83.1～125.6 a。

b) “或”重现期小于“且”重现期也小于设定的重现期，“或”重现期的风险率大于“且”重现期的风险率。分别以6个重现期为衡量标准，5个区域D与S联合分布的“或”重现期与“且”重现期之间都十分接近，反映整个雷州半岛出现干旱事件的风险概率基本相同。

c) 100年一遇“或”重现期风险率介于1%～2%之间、“且”重现期风险率介于0%～1%之间；50年一遇“或”重现期风险率介于2%～3%之间、“且”重现期风险率介于1%～2%之间；20年一遇“或”重现期风险率介于5%～7%之间、“且”重现期风险率介于3%～5%之间；10年一遇“或”重现期风险率介于10%～12%之间、“且”重现期风险率介于8%～10%之间；5年一遇“或”重现期风险率介于21%～24%之间、“且”重现期风险率介于17%～22%之间；2年一遇“或”重现期风险率介于53%～56%之间、“且”重现期风险率介于44%～50%之间。综上所述，2年一遇“或”重现期与“且”重现期风险率最高，说明重现期为2年一遇的干旱属于雷州半岛常态化事件，发生的风险较高。

采用式(4)—(7)分别以干旱历时1、2、3、4、5、6个月为条件，与重现期为2、5、10、20、50、100 a的干旱烈度设计值组合，计算遭遇条件概率P(S≥s|D≥d)和组合条件概率P(S≥s|D≤d)2种结果分布见图6。由图6可知，对干旱遭遇条件概率而言：1个月干旱历时条件下，各个区域干旱遭遇2年一遇的最大风险率基本大于85%；2个月干旱历时条件下，各个区域干旱遭遇2年一遇的最大风险率基本大于98%；3～6个月干旱历时条件下，各个区域干旱遭遇2年一遇的最大风险率等于1，进一步显示出在1～6个月干旱历时条件下，2年一遇干旱属于区域内常态化事件。对于干旱组合条件概率而言：1个月干旱历时条件下，各区域出现2年一遇的干旱烈度的风险率最大，随干旱烈度重现期加大而迅速归零；随着干旱历时增大到6个月，干旱烈度风险概率增大，在2～6个月干旱历时条件下，2年一遇干旱烈度发生风险率最大，进一步说明2年一遇的干旱烈度是影响区域内主要干旱事件，说明区域内干旱发生频率高。

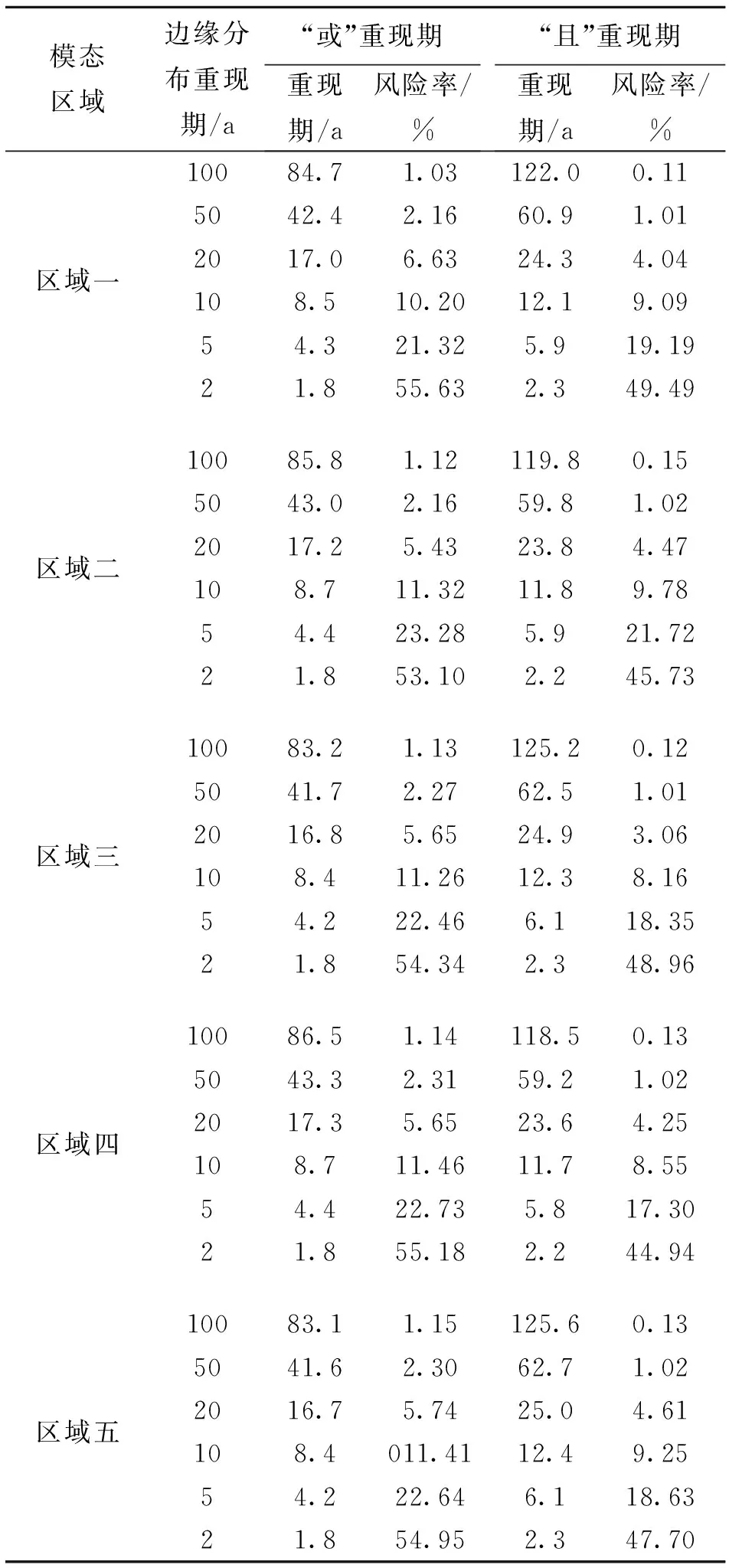
表6 “或”重现期和“且”重现期及其风险概率

a) 区域一P(S≥s|D≥d)的条件概率

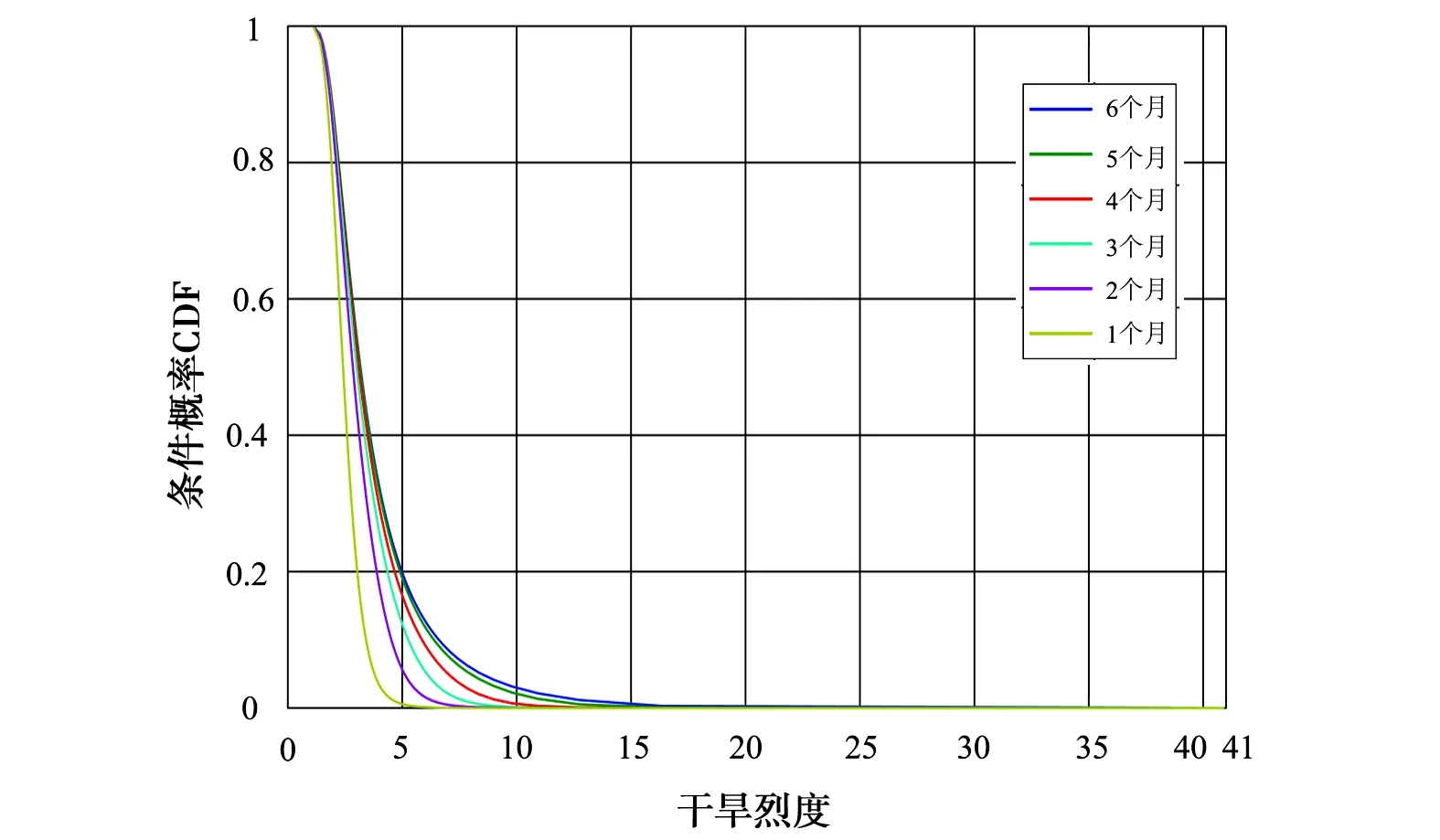
b) 区域一P(S≥s|D≤d)的条件概率

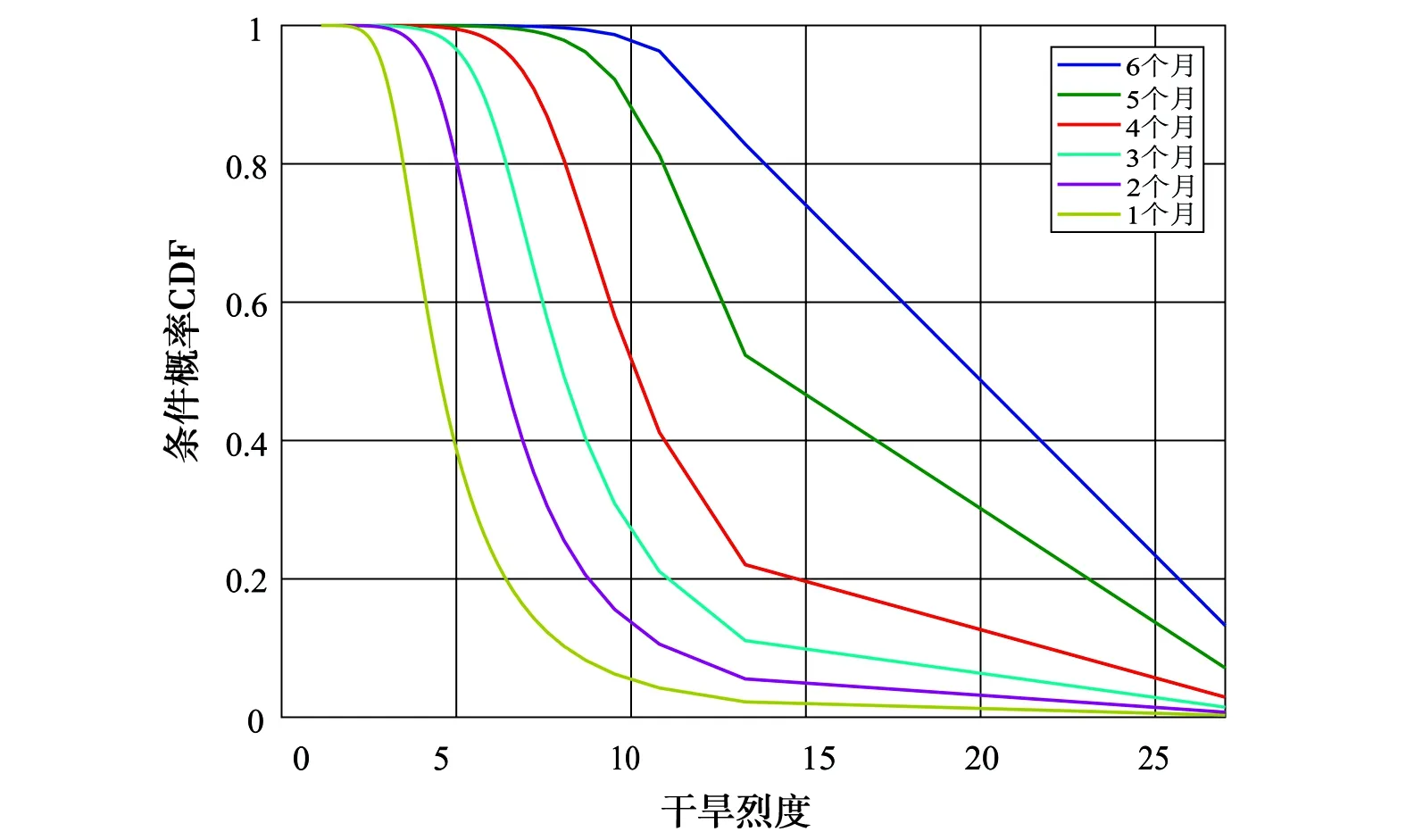
c) 区域二P(S≥s|D≥d)的条件概率

d) 区域二P(S≥s|D≤d)的条件概率

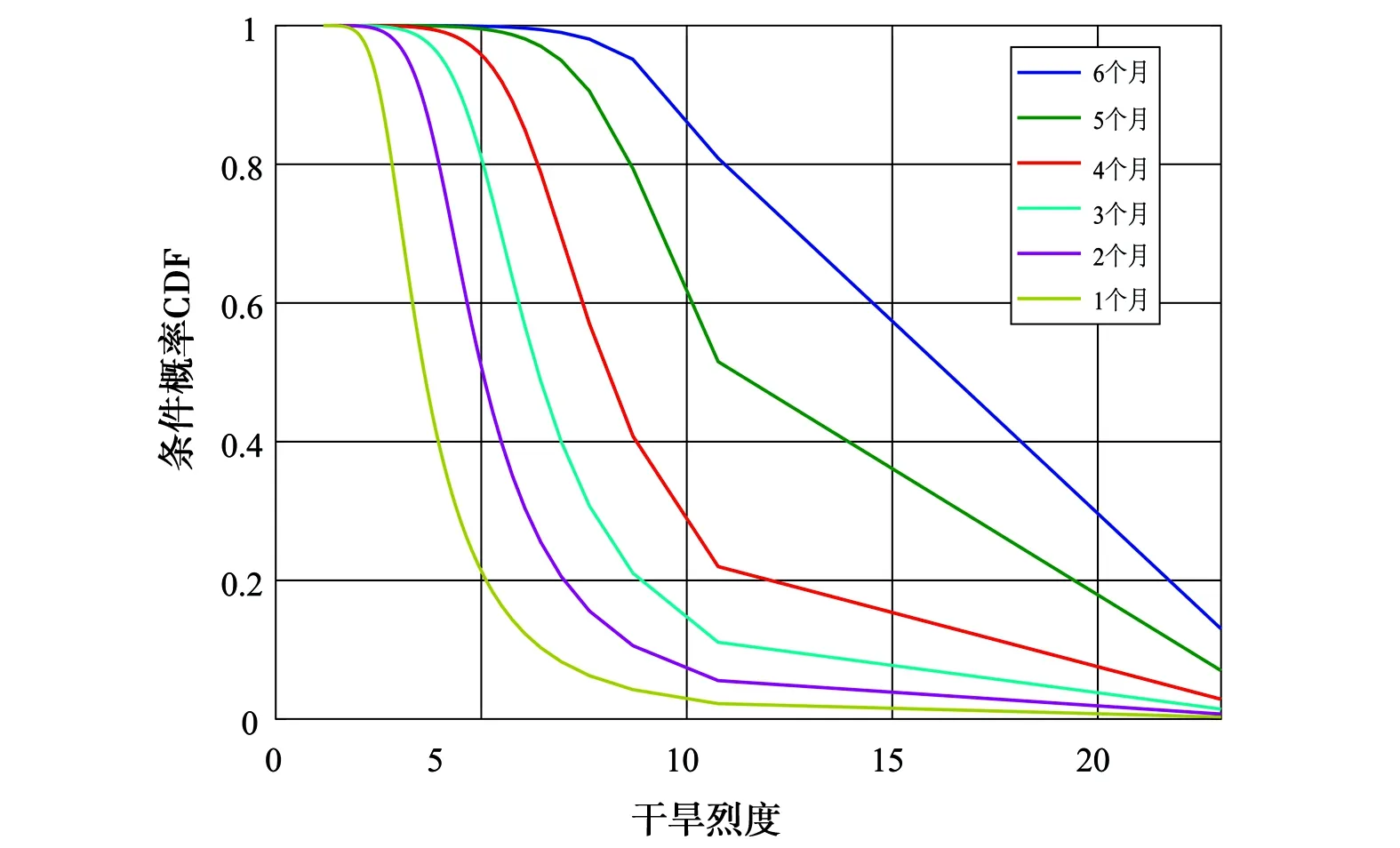
e) 区域三P(S≥s|D≥d)的条件概率

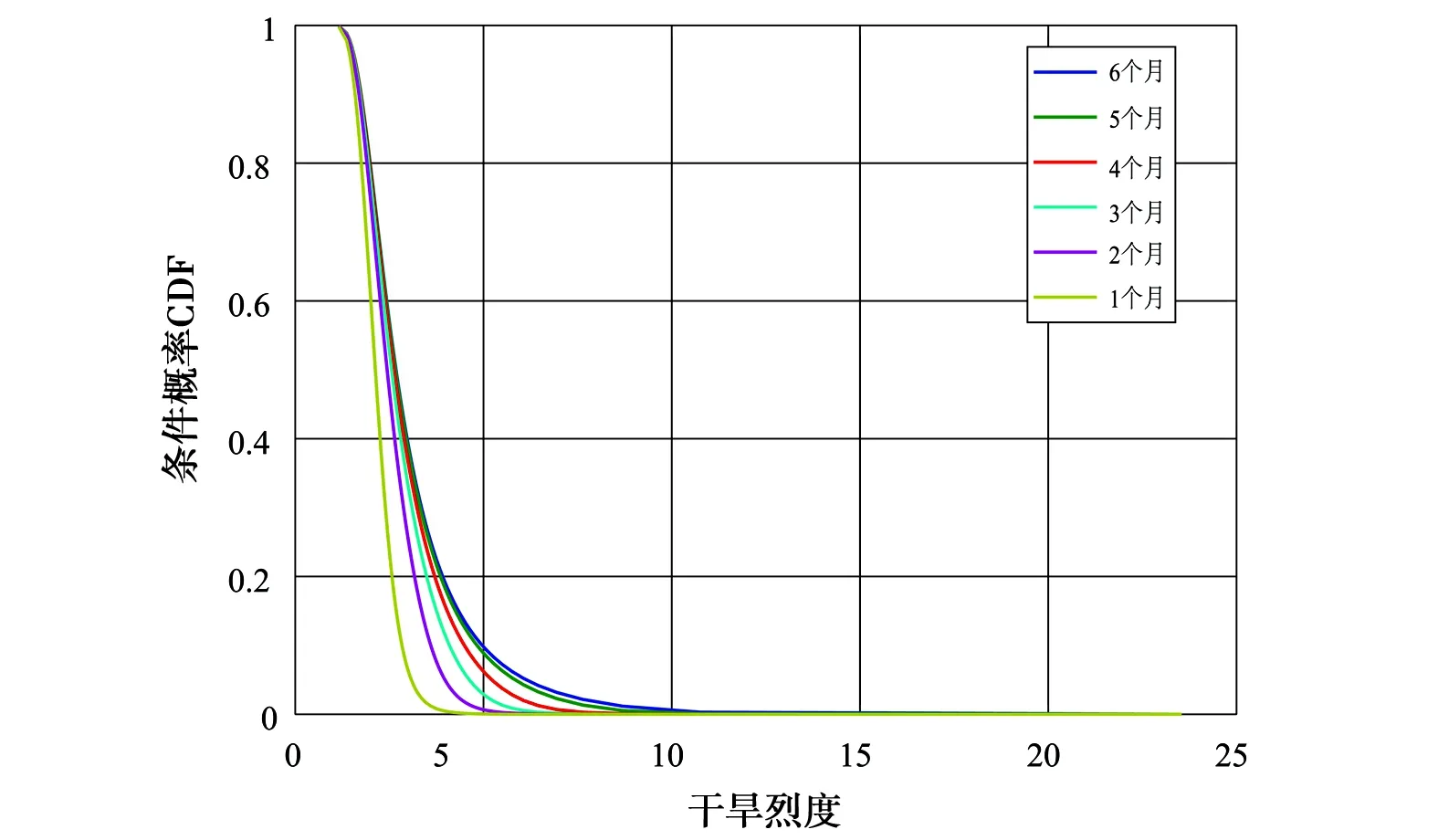
f) 区域三P(S≥s|D≤d)的条件概率

g) 区域四P(S≥s|D≥d)的条件概率

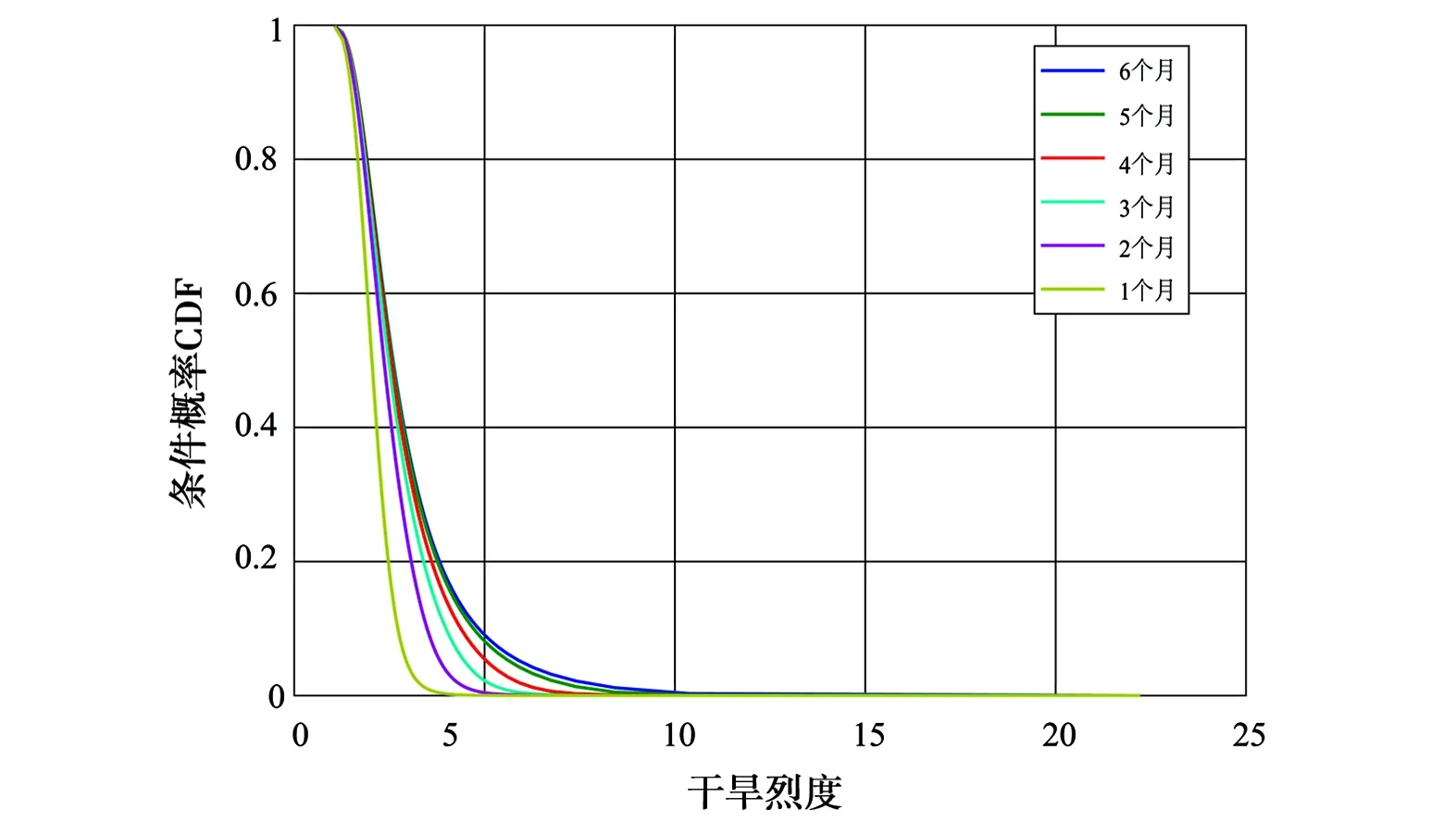
h) 区域四P(S≥s|D≤d)的条件概率

图6P(S≥s|D≥d)及P(S≥s|D≤d)条件概率分布

i) 区域五P(S≥s|D≥d)的条件概率

j) 区域五P(S≥s|D≤d)的条件概率续图6 P(S≥s|D≥d)及P(S≥s|D≤d)条件概率分布

3.3 讨论

雷州半岛地势低平，气流难以停滞，降雨量较少；东部多为沿海平原，地势低平，不利排洪，易产生洪涝灾害；西部位于高台地背风坡，降雨少且土质疏松，地表难以蓄水易出现干旱；南部徐闻县中部地区有较高的台地，来自大洋气流被台地阻挡，造成徐闻县西部背风坡降雨比东部迎风坡少，是历年来徐闻县西部及西南地区常年干旱的原因之一。干旱风险和条件概率分析结果表明，在2～6个月干旱历时条件下，2年一遇的干旱烈度是影响区域主要干旱事件，其次是5年一遇干旱烈度，说明雷州半岛干旱发生频率高，存在2～5 a的干旱周期。根据雷州半岛历年干旱记录，对1966—2015年期间干旱灾害发生情况进行统计，期间共有30 a发生了干旱，发生的频率占60.0%。1985—2000(除1997、1999年)、2003—2005、2007—2015年期间干旱年年发生，而1971—1976、1979—1980、1982—1984、2001—2002年期间无干旱发生，说明雷州半岛实际干旱发生存在2～6 a的周期。本次采用Copula函数计算得到的干旱发生重现期与历史数据统计结果基本一致，可以为区域干旱预警以及风险管理提供科学依据。孙卫国等发现厄尔尼诺事件一般存在2～7、8～20、30 a以上的尺度周期变化，其中2～7 a的周期振荡为主要的显著性周期变化[38]，说明雷州半岛干旱的发生与厄尔尼诺有着密切的关系。

4 结论

基于1966—2015年雷州半岛12个雨量站的逐月降雨资料，采用标准化降水指数(SPI)法、旋转经验正交分解法(REOF)及游程理论选取干旱历时D与干旱烈度S，采用G-H Copula函数建立了D与S的二维联合分布，对区域气象干旱发生风险进行了分析，主要结论如下。

a) 基于SPI6，采用REOF分析方法将雷州半岛气象干旱空间分布分解成5个空间模态，不同空间模态对应不同的区域，第一空间模态的荷载中心区域位于徐闻大部分区域；第二空间模态的荷载中心位于雷州西部地区；第三空间模态的荷载中心位于湛江市区；第四空间模态的荷载中心位于遂溪西部地区；第五空间模态的荷载中心位于遂溪的东南部及雷州的东北部地区。

b) 对不同区域给定6个重现期(100、50、20、10、5、2 a)，基于Copula函数建立D与S的联合分布模型，计算得到边缘分布的重现期介于“或”重现期和“且”重现期之间,联合分布的这两种重现期可以看作是边缘分布的两种极端情况；6个区域之间的干旱历时与干旱烈度联合分布的“或”与“且”两种重现期基本接近，反映整个雷州半岛出现干旱事件的风险概率基本相同。

c) 2年一遇“或”重现期风险率较高，介于53%～56%之间；2年一遇“且”重现期风险率较高，介于44%～50%之间，显示出2年一遇干旱属于雷州半岛主要的干旱事件。

d) 对干旱遭遇条件概率和组合条件概率进行分析，进一步显示出在2～6个月干旱历时条件下，2年一遇的干旱烈度是影响区域内主要干旱事件，说明雷州半岛干旱发生频率高。