Duffing混沌系统的电路仿真研究

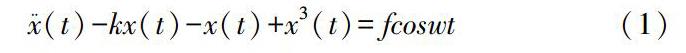
摘 要：借助Duffing参数敏感性来检测微弱的信号是当前有关领域研究的重点，文章在阐述Duffing系统及其电路实现的基础上，分析基于Duffing混沌系统的电路仿真设计，旨在能够更好的提升电路设计的精准度。

关键词：Duffing混沌系统;电路仿真;设计

近几年，伴随混沌理论在现代科学领域的广泛应用，人们开始将混沌理论应用在微弱信号的检测分析中，并根据研究应用不同类型的背景噪声形成了多种应用混沌来进行微弱信号检测的理论和方法。基于Duffing混沌系统对初始参数信息的敏感性，使其可以利用混沌振子提取和检测微弱信号。因此，从提升电路设计的精准度为基本出发点，就Duffing混沌系统的电路仿真设计问题进行探究。

1 Duffing混沌系统

Duffing方程是描述共振现象、调和振动、次调和振动、拟周期振动、概周期振动、奇异吸引子和混沌现象的一种模型。基于Duffing混沌系统的微弱信号检测常用方程如（1）表示。在公式中k代表的是阻尼比，fcoswt是内置激励信号，-x（t）+x3（t）表是系统非线性恢复力项。

2 Duffing混沌系统的电路特性

2.1 初始参数敏感性

基于Duffing混沌系统的初始参数敏感性是指在输入驱动正弦信号幅度数值较小的时候，相轨迹表现为poincare映射下的吸引子。在输入驱动正弦信号幅度数值超过一定阈值的时候将会出现同宿轨道的现象，且伴随输入驱动正弦信号幅度数值的增加，周期倍化将实现分叉，之后进入到混沌的状态，使得整个电路系统处于一种混沌的状态。

2.2 对不同频率的基本响应

导致Duffing混沌系统从混沌状态朝着大尺度周期转变的临界驱动有效电压并不完全相同，但是在一定有效位数上是相同的。对Duffing混沌系统进行仿真分析得到导致系统状态从混沌状态朝着大尺度周期态转变的临界驱动正弦信号幅度值为0.7256161.Duffing混沌系统仿真得到的最终结果和实际理论之间无法完全吻合。

3 仿真分析和讨论

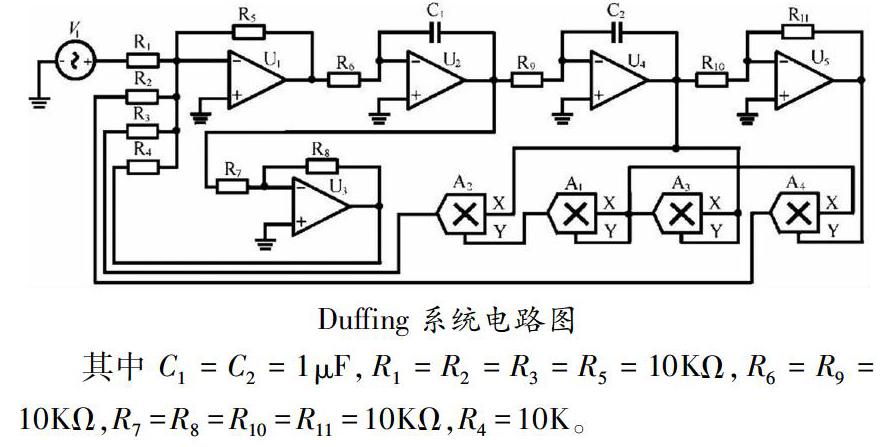
基于电路设计的基本原理，系统参数设置为k=-2，w=1rad/s，初值[x（0），x·（0）]=[0，0]，运用Mulitism软件对Duffing混沌系统（1）进行电路设计，其中电路中的运算放大器为LM741，模拟乘法器为AD633。其电路原理图如下图所示。

其中C1=C2=1μF，R1=R2=R3=R5=10KΩ，R6=R9=10KΩ，R7=R8=R10=R11=10KΩ，R4=10K。

3.1 积分环节参数对Duffing混沌系统电路频率和相频的影响

在对Duffing混沌系统电路分析之后发现，假定设定系统k是阻尼比，设定R4=20KΩ，除了R6和R9电阻之外，其他的电阻设定为10KΩ。改变R6、R9、C1和C2的数值，不管是改变哪个电阻数值，系统输出的数值一般就有低通特性。在C1和C2的增加情况下，幅频响应曲线也会朝着低频的方向移动。

3.2 不同内置激励信号频率对Duffing混沌系统电路相态的影响

假设R6=R9=10KΩ，C1=C2=0.1uF，在其他参数不改变的情况下改变内置激励信号的频率，并观察内置信号幅度数值在1V以及频率分别为50、100和150赫兹的情况。

根据分析观察之后发现，在内置信号V1的幅度为1V，频率为100Hz的时候，幅度频率变化曲线会出现转折变动，相频曲线的数值也会不断增大。在内置激励信号频率和相频曲线最大数值频率保持在一致状态的时候，混沌轨迹周期也会加大，相交的轨迹会处于一种混沌的状态。

3.3 不同系统非线性恢复力项对Duffing混沌系统灵敏度的影响

假设系统非线性恢复力项系数为1，假设激励信号是一种正弦信号，基本频率为100HZ，初始的相位为负180度，调节内置激励信号的临界数值，之后将调整好的数值加入到同频同相待检测信号中，信号的幅度发生了变化，四种幅度数值对应的状态为临界混沌态、临界混沌、临界混沌、大尺度周期。

4 结语

本文借助Mulitism软件对Duffing混沌系统电路进行仿真，在电路仿真分析的作用下得出环节参数对Duffing混沌系统检测频率的选择性。因此，在检测Duffing混沌信号时，需選择在内置激励信号频率最大的情况下进行，而设计电路时需考虑被检测信号的波形、内置激励信号波形、非线性恢复力项等一系列系数，为后续电路信号的检测提供重要参考支持。

参考文献：

[1]王永生，肖子才，孙瑾，等.Duffing混沌系统电路仿真研究[J].电路与系统学报，2008，13（1）.

[2]廖红华，于军，陈建军，等.基于Simplorer的Duffing混沌系统电路仿真与研究[J].电路与系统学报，2011（4）：125-130.

[3]韩保红，闫石，崔坤林.用反馈法主动控制Duffing混沌系统的仿真研究[J].航天控制，2002，20（3）.

作者简介：赵宁（1989-），男，汉族，河南项城人，讲师，主要研究方向：轨道交通信号与控制，混沌控制。