An ℓ-Step Modified Augmented Lagrange Multiplier Algorithm for Completing a Toeplitz Matrix

WEN Ruiping(温瑞萍),LI Shuzhen(李姝贞)

( Key Laboratory of Engineering & Computing Science,Shanxi Provincial Department of Education /Department of Mathematics,Taiyuan Normal University,Jinzhong 030619,China)

Abstract: Based on the modified augmented Lagrange multiplier (MALM) algorithm for Toeplitz matrix completion (TMC) proposed by WANG et al.(2016),we put forward an accelerated technique to MALM algorithm,which will reduce the extra load coming from data communication.It is drawn that an ℓ-step modified augmented Lagrange multiplier algorithm.Meanwhile,we demonstrate the convergence theory of the new algorithm.Finally,numerical experiments show that the ℓ-step modified augmented Lagrange multiplier(ℓ-MALM) algorithm is more effective than the MALM algorithm.

Key words: Toeplitz matrix;Matrix completion;Augmented Lagrange multiplier;Data communication

1.Introduction

Completing an unknown low-rank or approximately low-rank matrix from a sampling of its entries is a challenging problem applied in many fields of information science.For example,machine learning[1−2],control theory[11],image inpainting[4],computer vision[14]etc.Matrix completion (MC) problem first introduced by Cand`es and Recht[6]is from portion of the observed matrix elements to fill a low-rank matrix as precisely as possible,it is a hot spot of researching in recent years.The famous recommendation system of the Netflix[3]is the typical application of matrix completion.Mathematical language is expressed as follows:

where the matrixM∈Rm×nis the underlying matrix to be reconstructed,Ω ⊂{1,2,···,m}×{1,2,···,n} represents the random subset of indices for the known entries to the sampling matrixM,andPΩis associated sampling orthogonal projection operator onΩ.The purpose of the optimization problem is to reduce the rank of matrix obtained by filling missing elements as far as possible.In other words,the model (1.1) optimizes the structure of the matrix.

Although matrix completion needs solving the global solution of the non-convex objective problem,there are still many effective algorithms which are applicable to some specific matrix.Many researchers have suggested that the most of a low-rank matrix can be accurately completed according to the known entries at specified accuracy.In a low dimensional linear subspace,the meaning of precision is that we can realize the reasonable matrix completion under the hypothesis of the lowest-rank data matrix.

However,the optimization problem (1.1) is an NP-hard problem,in theory and practice,the computational complexity of the existing algorithms is a double exponential function about the matrix dimension.As a result,the computations are cumbersome and the data take up a large amount of computer memory.Therefore,the solving of the problem (1.1) is usually expensive by the existing algorithms.Hence,using the relation between the rank and the nuclear norm of a matrix,Cand`es and Recht[6]made the equivalent form of the problem(1.1) as follows:

whereM∈Rm×nis the underlying matrix,denotes thek-th largest singular value of ther-rank matrixA∈Rm×n,namelyσ1≥σ2≥···≥σk≥···≥σr >0.The problem (1.1) is transformed into a convex optimization problem which is easy to solve.

Academic circles have made abundant research results in solving the optimization problem (1.2) such as the augmented Lagrange multiplier (ALM) algorithm[9],the singular value theresholding(SVT)algorithm as well as its variants[5,8,19],the accelerated proximal gradient(APG)algorithm[15],and the modified augmented Lagrange multiplier(MALM)algorithm[17]etc.On the practical problems,the sampling matrix often has a special structure,for instance,the Toeplitz and Hankel matrices.Many scholars have conducted in-depth research on the special structure,property and application of the Toeplitz and Hankel matrix in recent years[10,12−13,16,18].As we well know,ann×nToeplitz matrix can be expressed as the following form:

which is determined by 2n−1 entries.

As for MALM algorithm,the intuitive idea is to switch iteration matrix into Toeplitz structure at each step by an operator.To implement this idea,a heavy data has to be moved at each iterate step.However,there is a cost,sometimes relatively great,associated with the moving of data.The control of memory traffic is crucial to performance in many computers.

In order to reduce the traffic jam of data,anℓ-step modified ALM algorithm is proposed in this paper.Compared with the MALM algorithm,the new algorithm saves computation cost and reduces data communication.Two aspects are taken into account,which result in a more practical or economic implementing.The new algorithm not only overcomes the slowness produced by the computing of singular value decomposition in ALM algorithm,but also saves the data congestion caused by the data communication in MALM algorithm.Compared with the CPU of the MALM algorithm,we can see that the CPU of theℓ-MALM algorithm is reduced to 45%.

Here are some of the necessary notations and preliminaries.Rm×ndenotes the set ofm×nreal matrix.The nuclear norm of a matrixAis denoted by‖A‖∗,the Frobenius norm by‖A‖Fis the sum of absolute values of the matrix entries ofA.ATis used to denote the transpose of a matrixA∈Rn×n,rank(A) stands for the rank ofAand tr(A) represents the trace ofA.The standard inner product between two matrices is denoted by〈X,Y〉=tr(XTY).Ω ⊂{−n+1,···,n−1}is the indices set of observed diagonals of a Toeplitz matrixM∈Rn×n,¯Ωis the complementary set ofΩ.For a Toeplitz matrixA∈Rn×n,the vector vec(A,l)denotes a vector reshaped from thel-th diagonal ofA,l=−n+1,···,n−1,PΩis the orthogonal projector onΩ,satisfying

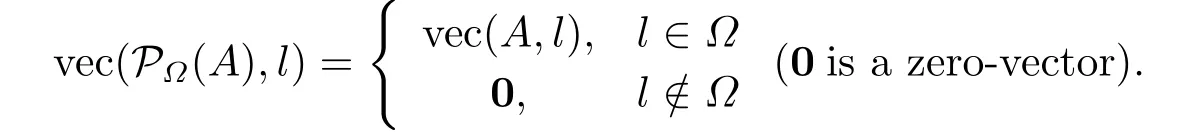
Definition 1.1(Singular value decomposition(SVD)) The singular value decomposition of a matrixA∈Rm×nofr-rank is defined as follows:

whereU∈Rm×randV∈Rn×rare column orthonormal matrices,σ1≥σ2≥···≥σr >0.

Definition 1.2(Singular value thresholding operator)[5]For eachτ≥0,the singular value thresholding operatorDτis defined as follows:

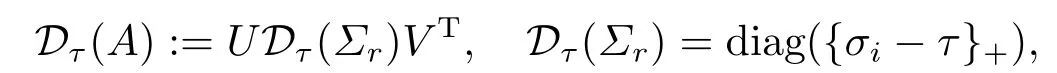
whereA=UΣrVT∈Rm×n,{σi−τ}+=

Definition 1.3The matrices

are called the basis of the Toeplitz matrix space.

It is clear that a Toeplitz matrixT∈Rn×n,shown in (1.3),can be rewritten as a linear combination of these basis matrices,that is,

Definition 1.4(Toeplitz structure smoothing operator) For any matrixA=(aij)∈Rn×n,the Toeplitz structure mean operatorTis defined as follows:

The rest of the paper is organized as follows.After we review briefly the ALM,MALM algorithms and the dual approach,anℓ-step modified ALM algorithm will be proposed in Section 2.Next,the convergence analysis is given in Section 3.Then the numerical results are provided to show the effectiveness of theℓ-MALM in Section 4.Finally,the paper ends with a conclusion in Section 5.

2.Relative Algorithms

Since the matrix completion problem is closely connected to the robust principal component analysis (RPCA) problem,then it can be formulated in the same way as RPCA,an equivalent problem of (1.2) can be considered as follows.In terms of estimating the lowdimensional subspace,the purpose of the mathematical model is to find a low-rank matrixA∈Rm×n(as long as the error matrixEis sufficiently sparse,relative to the rank ofA)to minimize the difference between matrixAandM,generating the following constraint optimization problem model:

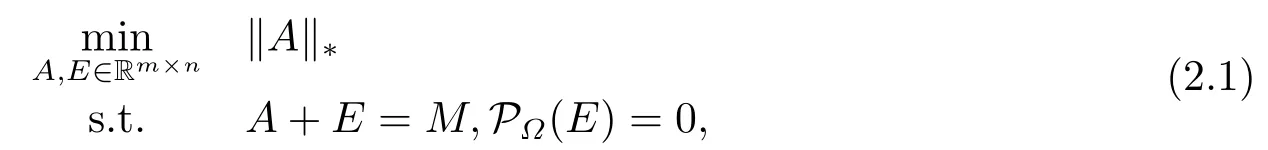
whereEwill compensate for the unknown entries ofM,the unknown entries ofM∈Rm×nare simply set as zeros.AndPΩ:Rm×n→Rm×nis a linear operator that keeps the entries inΩunchanged and sets those outsideΩ(say,in) zeros.Then we introduce the algorithm for solving problem (2.1).

ⅠThe augmented Lagrange multiplier (ALM) algorithm

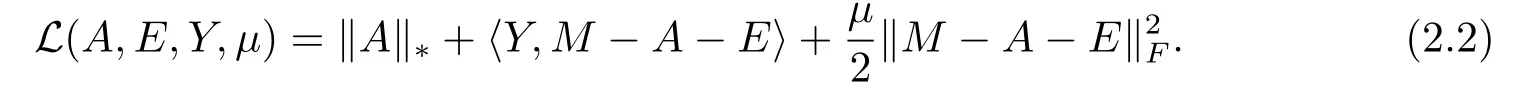
It is famous that partial augmented Lagrangian function of the problem (2.1) is Hence,the augmented Lagrange multiplier (ALM) algorithm[9]is designed as follows.

Algorithm 2.1Step 0 GiveΩ,sampled matrixD=PΩ(M),µ0>0,ρ >1.Give also two initial matricesY0=0,E0=0.k:=0;

Step 1 Compute the SVD of the matrix (D−Ek+µk−1Yk),

Step 2 Set

SolveEk+1=arg

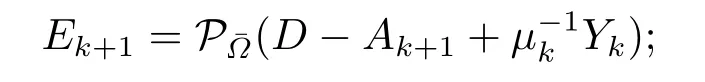
Step 3 If‖D−Ak+1−Ek+1‖F/‖D‖F <ϵ1andµk‖Ek+1−Ek‖F/‖D‖F <ϵ2,stop;otherwise,go to Step 4;

Step 4 SetYk+1=Yk+µk(D−Ak+1−Ek+1).Ifµk‖Ek+1−Ek‖F/‖D‖F <ϵ2,setµk+1=ρµk;otherwise,go to Step 1.

RemarkIt is reported that the ALM algorithm performs better both in theory and algorithms than the others that with a Q-linear convergence speed globally.It is of much better numerical behavior,and it is also of much higher accuracy.However,the algorithm has a disadvantage of the penalty function:the matrix sequences{Xk} generated by Algorithm 2.1 are not feasible.Hence,the accepted solutions are not feasible.

ⅡThe dual algorithm

The dual algorithm proposed in [7]tackles the problem (2.1) via its dual.That is,one first solves the dual problem

for the optimal Lagrange multiplierY,where

A steepest ascend algorithm constrained on the surface{Y|J(Y)=1}can be adopted to solve(2.3),where the constrained steepest ascend direction is obtained by projectingMonto the tangent cone of the convex body{Y|J(Y)≤1}.It turns out that the optimal solution to the primal problem (2.1) can be obtained during the process of finding the constrained steepest ascend direction.

ⅢThe modified augmented Lagrange multiplier (MALM) algorithm

In this pant,we mention a mean-value technique for TMC problem[17].The problem can be expressed as the following convex programming,

whereA,M∈Rn×nare both real Toeplitz matrices,Ω ⊂{−n+1,···,n−1}.LetD=PΩ(M).Then the partial augmented Lagrangian function is

whereY∈Rn×n.

Algorithm 2.2Step 0 GiveΩ,sampled matrixD,µ0>0,ρ >1.Give also two initial matricesY0=0,E0=0.k:=0;

Step 1 Compute the SVD of the matrix (D−Ek+) using the Lanczos method

Step 2 Set

Step 3 If‖D−Ak+1−Ek+1‖F/‖D‖F <ϵ1andµk‖Ek+1−Ek‖F/‖D‖F <ϵ2,stop;otherwise,go to Step 4;

Step 4 SetYk+1=Yk+µk(D−Ak+1−Ek+1).Ifµk‖Ek+1−Ek‖F/‖D‖F <ϵ2,setµk+1=ρµk;otherwise,go to Step 1.

RemarkIt is reported that MALM algorithm performs better that of much higher accuracy.Compared with the ALM,APGL,and SVT algorithms,the MALM algorithm is advantageous over the other three algorithms on the time costed by the SVD for smoothing at each iterate.

As we know,the saving of the SVD time is at the expense of data communication.Sometimes,this is not worth the candle.This motivated us to put up with the following algorithm.

ⅣTheℓ-step modified augmented Lagrange multiplier (ℓ-MALM) algorithm

To reduce the workload of data being moved at each iteration step,we propose a new accelerated algorithm for the TMC problem,which is smoothing once the diagonal elements of the iteration matrix by (1.5) for everyℓsteps.The technique saves computation cost and reduces the data communication.It turns out that the iteration matrices keep a Toeplitz structure,which ensure the fast SVD of Toeplitz matrices can be utilized.

Algorithm 2.3(ℓ-MALM algorithm)

Input:Ω,sampled matrixD,Y0,0=0,E0,0=0;parametersµ0>0,ρ >1,ℓ,ϵ1,ϵ2.Letk:=0,q:=1,q=1,2,···,ℓ−1.

Repeat:

Step 1ℓ−1 iterations.

1) Compute the SVD of the matrix (D−Ek,q+) using the Lanczos method

2) Set

3) If‖D−Xk+1,q+1−Ek+1,q+1‖F/‖D‖F <ϵ1andµk,q‖Ek+1,q+1−Ek,q‖F/‖D‖F <ϵ2,stop;otherwise,go to Step 1 4);

4) SetYk+1,q+1=Yk,q+µk,q(D−Xk+1,q+1−Ek+1,q+1),µk+1,q+1=ρµk,q;otherwise,go to Step 1 1);

Step 2ℓ-th smoothing.

1) Compute

UpdateEk+1,ℓ=

Step 3 If‖D−Ak+1,ℓ−Ek+1,ℓ‖F/‖D‖F <ϵ1andµk,ℓ‖Ek+1,ℓ−Ek,ℓ‖F/‖D‖F <ϵ2,stop;otherwise,go to Step 4;

Step 4 SetYk+1,q+1=Yk,q+µk,q(D−Ak+1,q+1−Ek+1,q+1).

Ifµk,q‖Ek+1,q+1−Ek,q‖F/‖D‖F <ϵ2,setµk+1,q+1=ρµk,q;otherwise,go to Step 1.

RemarkClearly,this algorithm is an acceleration of the MALM algorithm in [17].Whenℓ=1,it becomes the MALM scheme.

3.Convergence Analysis

We provided first some lemmas in the following.

Lemma 3.1[6]LetA∈Rm×nbe an arbitrary matrix andUΣVTbe its SVD.Then the set of subgradients of the nuclear norm ofAis provided by

∂‖A‖∗={UVT+W:W∈Rm×n,UTW=0,WV=0,‖W‖2≤1}.

Lemma 3.2[9]Ifµkis nondecreasing then each term of the following series is nonnegative and the series is convergent,that is,

Lemma 3.3[9]The sequences{},{Yk}and{}are all bounded,where=Yk+1+µk−1(D−Ak−Ek−1).

Lemma 3.4The sequence{Yk,q} generated by Algorithm 2.3 is bounded.

ProofLetdefined as (1.5).

First of all,we indicate thatYk,q,Ek,q,k=1,2,···,q=1,2,···,ℓ−1 are all Toeplitz matrices.Evidently,Y0,0=0,E0,0=0 are both smoothed into Toeplitz matrices.Suppose that afterYk,q,Ek,qare both Toeplitz matrices,so isEk+1,q+1=Thus,Yk+1,q+1is a Toeplitz matrix also from the Step 4 in Algorithm 2.3.

And,

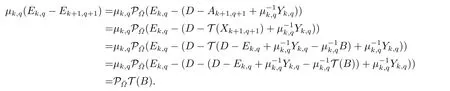
It is clear that by Steps 1-2 in Algorithm 2.3,

Hence we can obtain thatYk,q+µk,q(D−Ak+1,q+1−Ek,q)∈∂‖Ak+1,q+1‖∗from Lemmas 3.2 and 3.3.It is known that forAk+1,q+1=UΣVTby Lemma 3.1,

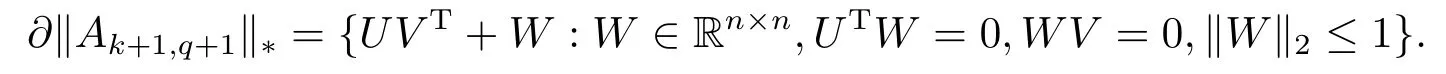
We have also,

Therefore,the following inequalities can be obtained:

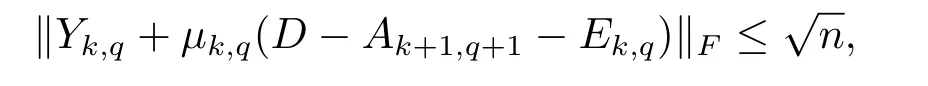
and

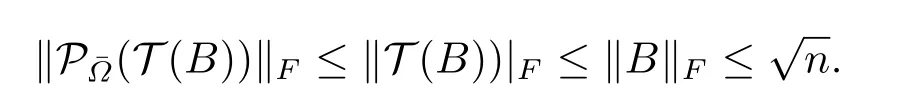
It is clear that the sequence{Yk,q} is bounded.

Theorem 3.1Suppose thatthen the sequence{Ak,q} converges to the solution of (2.5) whenµk,q→∞and

ProofIt is true that

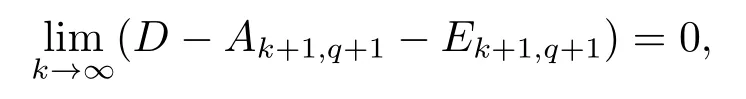
since(Yk+1,q+1−Yk,q)=D−Ak+1,q+1−Ek+1,q+1and Lemma 3.4.Let (Ä,Ë) be the solution of (2.5).ThenAk+1,q+1,Yk+1,q+1,Ek+1,q+1,k=1,2,···,are all Toeplitz matrices from+=D.We prove first that where=Yk,q+µk,q(D−Ak+1,q+1−Ek,q),is the optimal solution to the dual problem (2.3).

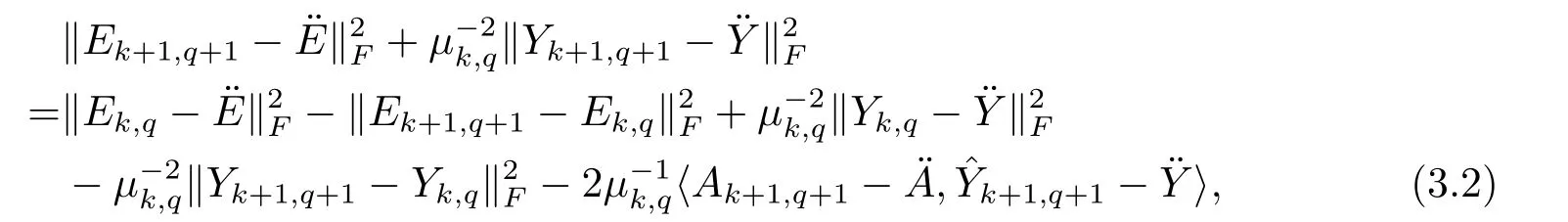
We obtain the following result through the same analysis,

Then

holds true.

On the other hand,the following is true by Algorithm 2.3:

Moreover,along the same idea of Theorem 2 in [9],it is obtained thatis the solution of(2.5).

Theorem 3.2LetX=(xij)∈Rn×n,T(X)=()∈Rn×nbe the Toeplitz matrix derived fromX,introduced in (1.5).Then for all Toeplitz matrixY=(yij)∈Rn×n,

ProofBy the definition ofT(X),we have=0,i,j=1,2,···,n.SinceYis a Toeplitz matrix,andyl=yij,l=i−j,i,j=1,2,···,n.Then

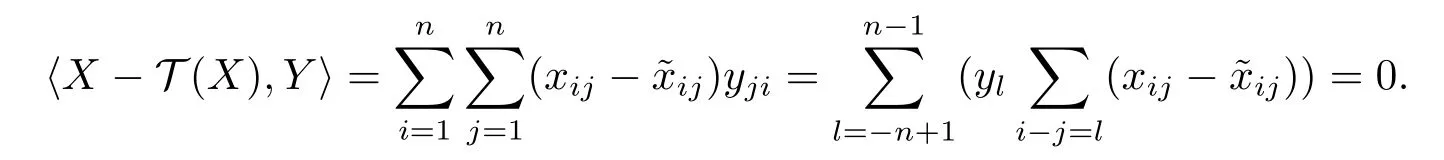
Theorem 3.3In Algorithm 2.3,Ak,qis a Toeplitz matrix derived byXk,q.Then

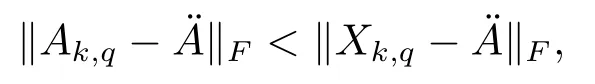
whereÄis the solution of (2.5).

Proof

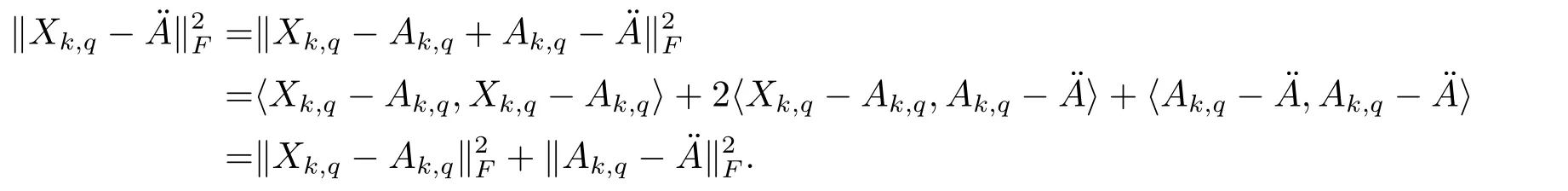
4.Numerical Experiments

In this section,some original numerical results of two algorithms(MALM,ℓ-MALM)are presented for then×nmatrices with different ranks.We conducted numerical experiments on the same and modest workstation.By analyzing and comparing iteration numbers (IT),computing time in second (time(s)),deviation (error 1,error 2) and ratio which are defined in the following,we can see that theℓ-MALM algorithm proposed by this paper is far more effective than the MALM algorithm.

In our experiments,M∈Rn×nrepresents the Toeplitz matrix.We select the sampling densityp=m/(2n−1),wheremis the number of the observed diagonal entries ofM,then 0≤m≤2n−1.With regard to theℓ-MALM algorithm,we set the parametersτ0=1/‖D‖2,δ=1.2172+,ϵ1=10−9,ϵ2=5×10−6andℓ=3 as a rule of thumb.The parameters of the MALM algorithm take the same as theℓ-MALM algorithm.

The experimental results of two algorithms are shown in Tables 4.1-4.4.From the tables,two algorithms can successfully calculate the approximate solution of prescriptive stop condition for all the test matricesM.And ourℓ-MALM algorithm in computing time is far less than that of the MALM algorithm.In particular,compared with the CPU of the MALM algorithm,we can find that the CPU of theℓ-MALM algorithm is reduced to 45%.The“ratio”in Table 4.5 can show this effectiveness.

Table 4.1 Comparison between MALM and ℓ-MALM for p=0.6.

Table 4.3 Comparison between MALM and ℓ-MALM for p=0.4.

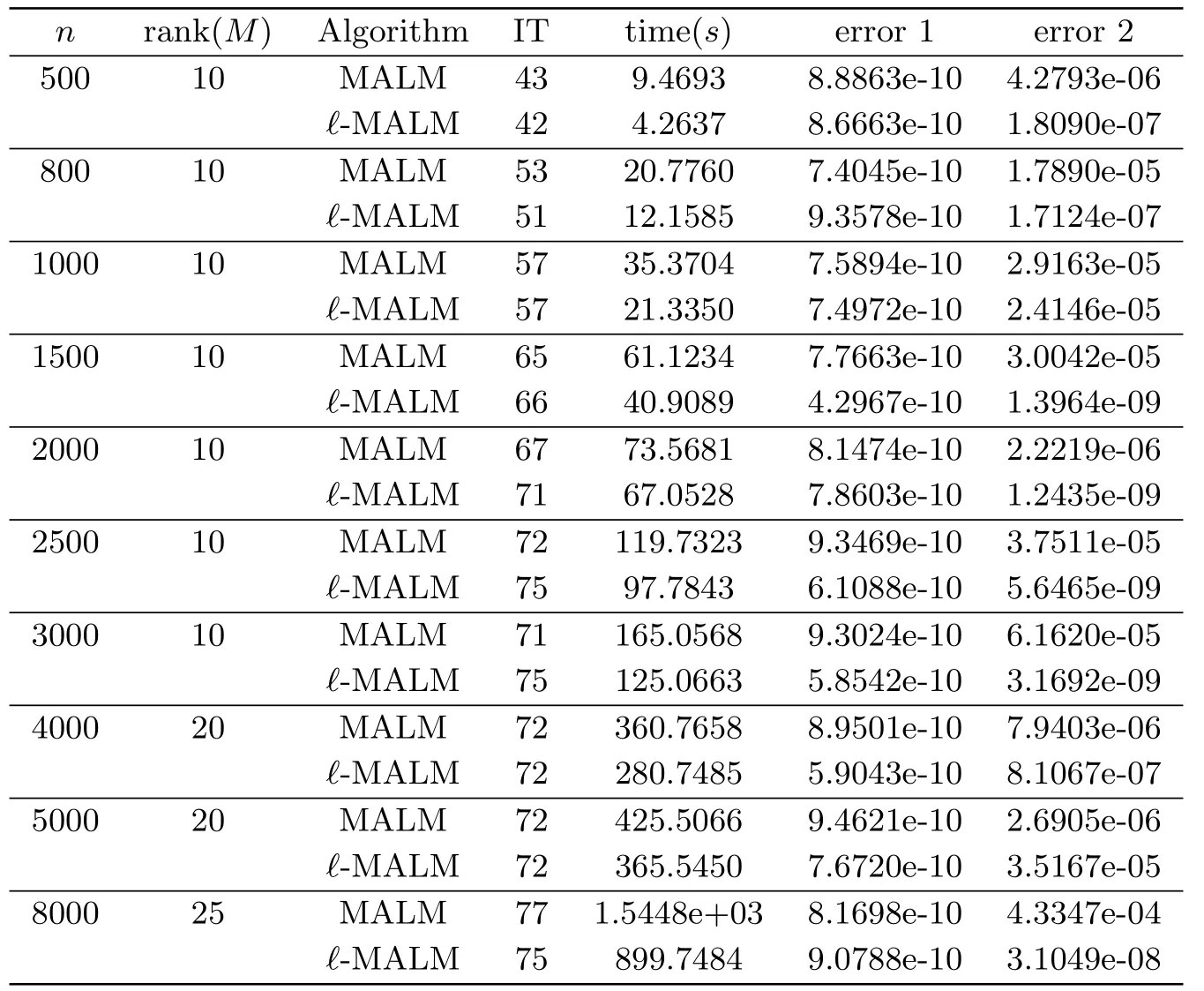
Table 4.4 Comparison between MALM and ℓ-MALM for p=0.3.

Table 4.5 The values of ratio.

5.Conclusion

As is known to all,matrix completion is usually to recover a matrix from a subset of the elements of a matrix by taking advantage of low rank structure matrix interdependencies between the entries.It is well-known but NP-hard in general.In recent years,Toeplitz matrix completion has attracted widespread attention and TMC is one of the most important completion problems.In order to solve such problems,we put forward anℓ-step modified augmented Lagrange multiplier (ℓ-MALM) algorithm based on the MALM algorithm,and corresponding with the theory of the convergence of theℓ-MALM algorithm are established.Theoretical analysis and numerical results have shown that theℓ-MALM algorithm is effective for solving TMC problem.Theℓ-MALM algorithm overcomes the original ALM algorithm both singular value decomposition of tardy,and surmounts the property of the extra load of the MALM algorithm.The reason is that data communication congestion is far more expensive than computing.Compared with the CPU of the MALM algorithm,we can see that the CPU of ourℓ-MALM algorithm is reduced to 45%.Therefore,ℓ-MALM algorithm has better convergence rate for solving TMC problem than the MALM algorithm (tables 4.1-4.5).

AcknowledgmentsThe authors gratefully acknowledge the anonymous referees and Professor ZZ Bai(academy of mathematics and systems science,Chinese academy of sciences)for their helpful comments and suggestions which greatly improved the original manuscript of this paper.