一类p-Laplace方程非局部边值问题解的性态研究
2019-10-16付美美谢君辉
付美美,谢君辉
( 湖北民族大学理学院,湖北 恩施445000)
1.引言
本文主要讨论如下非局部边值条件的p-Laplace抛物型问题:
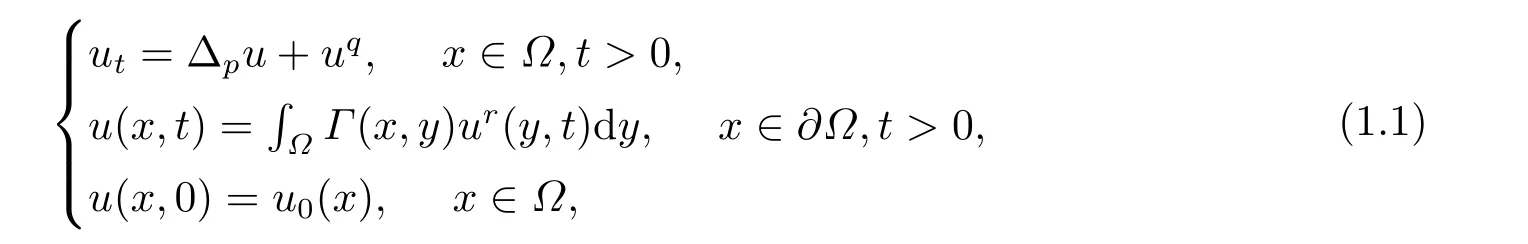
其中q >1,0 抛物型方程是一类重要的偏微分方程,它可以用来描述自然界中大量存在的扩散现象,例如在化学扩散,生物种群及渗流理论等领域都提出了各种抛物型方程来描述扩散现象.这些模型中一类很重要的模型为来自非牛顿流体理论的非牛顿渗流方程[1](抛物型p-Laplace方程): 已有很多的数学研究人员对含有p-Laplace算子的初边值问题进行了深入的探讨和研究.1972年,Tsutsumi[2]研究了如下问题 文[2]中得出:当p >2+α时,对任何初值,问题都存在一个非负的全局解.当2 带p-Laplace算子的非局部边值问题是偏微分方程边值问题的一个推广,这类问题从多孔介质中气体的湍流理论以及非牛顿流体理论中产生,由于具退化性质的非线性方程比线性方程和不具退化性的拟线性方程更能精确地刻画实际的物理现象,许多作者研究了在不同边值条件下p-Laplace抛物型方程解的一些问题.例如,解的存在性和大时间性态[3−5]、全局正则性[6]以及爆破[7−8],此外,反应项带有局部源和非局部源的抛物问题也得到了广泛研究[9−11]. 同时,由于边界项等形成的各种耦合关系而导致问题解的不同性质也引起了众多学者的兴趣,非线性边界条件可以描述为非线性扩散率,例如,热量由边界提供等.王荣年和王艳[7]研究了如下非局部非线性边值条件的渗流方程 正解的整体存在性、爆破和爆破速率,其中m >1,0 本文中,主要利用抛物方程上下解的方法及抛物方程的一些基本理论来证明解的整体存在性,以及在有限时刻爆破和爆破速率的估计等结论.我们研究非局部边界条件下,p-Laplace抛物型方程解的全局存在性及爆破性质、爆破发生的条件以及爆破发生的时间.得出的结论如下: 定理1.1若0 Ω Γ(x,y)dy≥1,x∈Ω,则问题(1.1)的解在有限时刻爆破. 定理1.2若0 Ω Γ(x,y)dy≤1,x∈Ω,则 (i)当u0(x)充分小时,问题(1.1)的解整体存在; (ii)当u0(x)充分大时,问题(1.1)的解在有限时刻爆破. 定理1.3若0 本节给出一些定义和预备知识,以备后面各节使用. 定义2.1[12]记u(x,t)为问题(1.1)的古典解,Tmax为u(x,t)的最大存在时间,若Tmax=+∞,则称问题(1.1)的解u(x,t)整体存在,或者问题(1.1)的解是全局存在的;若Tmax<+∞,且则称问题(1.1)的解u(x,t)在有限时刻爆破. 记QT=Ω×(0,T),∂QT=∂Ω×[0,T)∪Ω×{t=T},下面给出问题(1.1)上解和下解的定义. 定义2.2[13]如果(x,t)∈C2,1(QT)∩C(QT∪∂QT),且满足 则称函数(x,t)为问题(1.1)的上解. 定义2.3[13]如果且满足 则称函数(x,t)为问题(1.1)的下解. 引理2.1[13−14]如果和分别为问题(1.1)的非负上解和非负下解,且满足u(x,0)(x,0),则对任意的(x,t)∈QT,有 定理1.1的证明令T=0≤ω0≤假如ω(t)是如下问题 的解,经过简单计算,不难得到 从而,ω(t)≤1,又因为0 此外,由于ω(t)=ω0≤则ω(t) 是问题(1.1)的下解.事实上,当时,即ω(t) 在有限时刻爆破. 综上,问题(1.1)的解u(x,t)在有限时刻爆破. 定理1.2的证明(i) 令H(x) 为如下椭圆问题 的唯一正解,则当(x,y)dy <1时,存在常数δ >0,使得δ≤H(x)≤1,令H1(x)=作函数J(x)=CH(x),其中C为常数且C≥δ−1,从而J(x)=CH(x)≥δ−1δ=1,于是由Ω Γ(x,y)dy <1可知,J(x)|∂Ω=CH(x)|∂Ω=≥其中0 由此说明,若能证明J(x)是问题(1.1)的一个上解,由引理2.1可知,问题(1.1)的解整体存在. 下面,证明J(x)是问题(1.1)的一个上解,事实上,若Cδ0−CqH1q≥0,即C≥则Jt≥△pJ+Jq.此外,若CH2≥即且由于u0(x)足够小,得到J(0)≥u0(x),从而,取有: 即J(x)是问题(1.1)的一个上解.综上,当(x,y)dy <1 时,问题(1.1)的解整体存在. (ii) 接下来证明,当u0(x)充分大的时候,问题(1.1)的解在有限时刻爆破.考虑如下初边值问题: 假设h(x,t)为问题(3.4)的解,那么h(x,t)必为(1.1)的下解.同时,由引理2.1可知,h(x,t)≤u(x,t),(x,t)∈QT.对问题(3.4)中的第一个等式两边同时在Ω上积分,利用格林公式简单计算可得其中为∂Ω上的单位外法向量.因此,我们得: 当t→时,f(t)→∞,f(t)在有限时刻爆破,从而u(x,t)在有限时刻爆破. 定理1.3的证明令ψ+λuq=ut,则qψuq−1=quq−1ut−qλu2q−1,从而,取λ为足够小的正数时,可得ψt−△pψ+quq−1ψ≥0.对固定的(x,t)∈∂Ω×(0,T),我们有 又已知存在正常数,使得△pu0≥(λ−1)uq0,于是,对任意的x∈Ω,有ψ(x,0)=△pu0+(1−λ)uq0≥0. 另一方面,对固定的(x,t)∈∂Ω×(0,T),直接计算可得: 又因为 因此, 由(3.9)可得,ψ(x,t)≥0,∀(x,t)∈Ω×[0,T],从而, 对(3.10)式在(t,T)上积分,我们得到:u(x,t)≤ 本文对一类p-Laplace热方程解的整体存在性、解的爆破和爆破速率进行了讨论,先是对权函数给予了适当的条件,然后利用抛物型方程的上下解方法来证明了解的整体存在性和有限时刻爆破的结论,并给出了爆破速率的估计.不难看出,与一般的Dirichlet边界条件相对比,权函数Γ(x,y)对问题(1.1)解的整体存在与否起着相当重要的作用.我们的结果改进了文献的相关结果,但仍有许多待研究的问题: (i) 对于0≤r≤1的情形,是否存在相应的临界指数以及能否刻画该抛物型方程的爆破,到现在依然是一个开问题; (ii) 对于更一般的情形,即ut=∆pum+uq的时候,依然没有合适的爆破或者存在性结果; (iii) 对于不加确定条件的情况,即权函数Γ(x,y)不加限定条件,仍然无法判断临界情形是否属于爆破情形.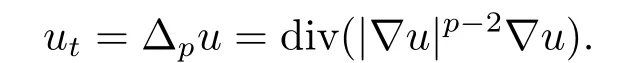


2.预备知识


3.主要结果的证明


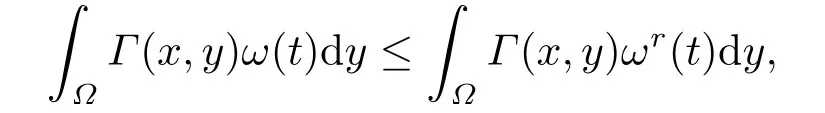
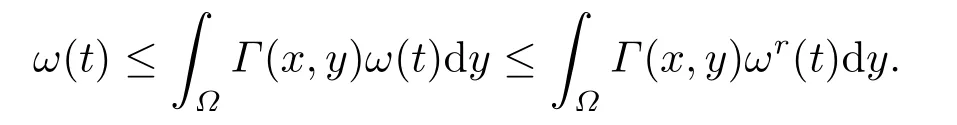
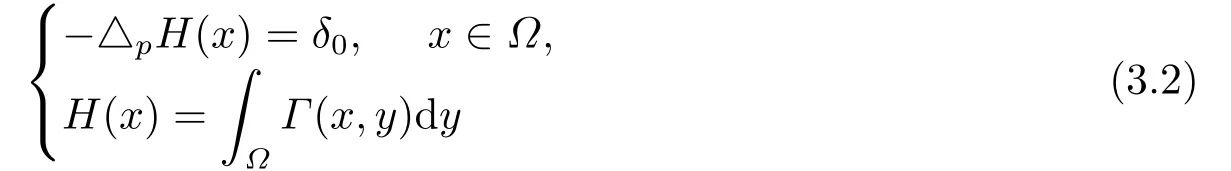
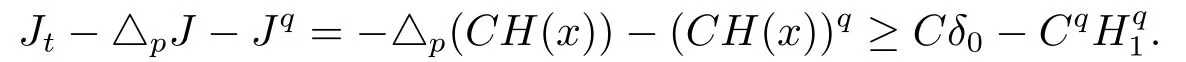



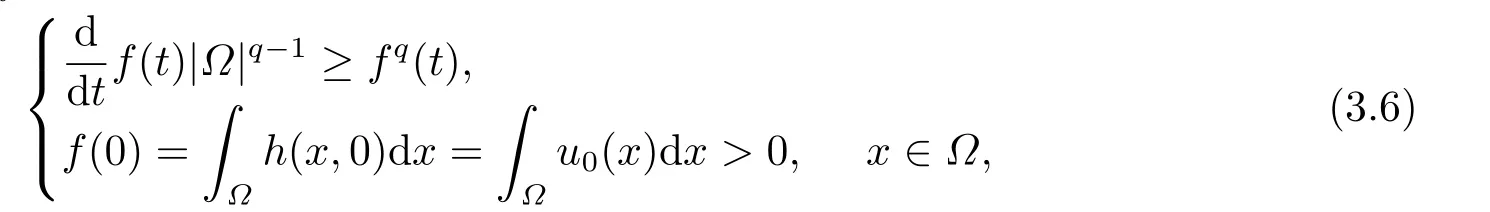

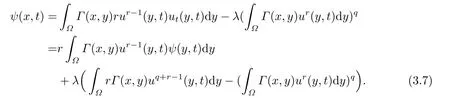



4.总结与展望
猜你喜欢
杂志排行
应用数学的其它文章
- 凸二次半定规划一个新的原始对偶路径跟踪算法
- Numerical Solution of Nonlinear Stochastic Itô-Volterra Integral Equations by Block Pulse Functions
- 面板数据分位数回归模型的工具变量估计
- Stability Analysis of Indirect Adaptive Tracking Systems for Simple Linear Plants with Unknown Control Direction
- The Boundedness of Maximal Dyadic Derivative Operator on Dyadic Martingale Hardy Space with Variable Exponents
- Positive Solutions for Kirchhoff-Type Equations with an Asymptotically Nonlinearity
