A New Exceptional Family of Elements for Complementarity Problems
2019-10-16CHENYu陈玉CHENCuiling陈翠玲HANCaihong韩彩虹
CHEN Yu(陈玉),CHEN Cuiling(陈翠玲),HAN Caihong(韩彩虹)
(School of Mathematics and Statistics,Guangxi Normal University,Guilin 541004,China)
Abstract: In this paper,we present a generalized exceptional family of elements for complementarity problems,which is a generalization for the concepts of exceptional family of elements and d-orientation sequence for a continuous function.We show that if there exists no generalized exceptional family for a continuous function,then the corresponding complementarity problem has a solution.It is also shown that a continuous function does not possess the generalized exceptional family under Karamardian type condition,Isac and Gowda type condition or p-order generalized coercive type condition.Applying the new concept to the P∗-mapping CP,a new existence result is established.
Key words: Complementarity problem;Exceptional family of element; P∗-mapping
1.Introduction
A complementarity problem (CP for short) is to find az∈Rnsuch that
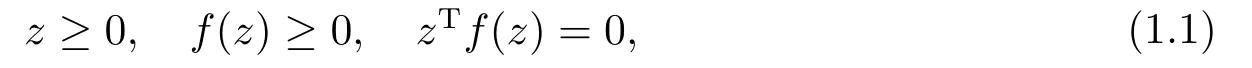
wheref:Rn→Rnis a continuous function.It is known that CP(1.1) has many wide applications in economics,engineering,operation research etc.[1]CP(1.1) has received increasing attention recently.The research of the existence conditions of the solution for CP(1.1) has played an important role in both theory and practical applications.Among these researches,the concept of exceptional family is a very powerful tool to study the existence properties of the solution to CP(1.1) and variational inequality(VI for short) problems.Smith[2]firstly presented the concept of exceptional family of elements for a continuous function.Subsequently,a more general notion of exceptional family of elements was introduced by Isac[3].Based on this notion,some results on existence of solutions to nonlinear complementarity problems were established in [3-4].Exceptional family of elements is also extended by ZHAO et al.[5−8]to study the existence conditions of solutions to variational inequality problems.Recently,this notion is extended to study the existence theorems of solutions to semidefinite complementarity problems and copositive cone complementarity problem[9−14].In[15],ZHAO presented thed-orientation sequence concept for a continuous function which is different from other notions of exceptional family of elements,and he proved some similar properties as that of the exceptional family of elements.
In this paper,motivated by the previous studies,we introduce a new concept of exceptional family of elements for a continuous function,which unifies the two concepts ofd-orientation sequence and exceptional family of elements for a continuous function.We prove that if there exists no generalized exceptional family for a continuous function,then CP(1.1) has a solution.Under the Karamardian type condition,Isac and Gowda tpye condition orp-order generalized coercive type condition,the property that a continuous function does not possess the generalized exceptional family is established,respectively.By applying the new concept to theP∗-mapping CP,a new existence result is presented.
2.Generalized Exceptional Family of Elements
Throughout this paper,letf:Rn→Rnbe a continuous function and letd∈Rnbe a given vector with positive orthant,i.e.,d >0.firepresents thei-th component of a vectorvalued functionfand similar notations are used for vectors.In this section,we first recall the concepts about the exceptional family of elements andd-orientation sequence forf.
Definition 2.1[3]Let{zr} ⊂Rn+be a set of points,{zr} is defined as an exceptional family of elements forfwith respect to Rn+if‖zr‖→∞asr→∞,and for eachzrthere exists a scalarµr >0 such that
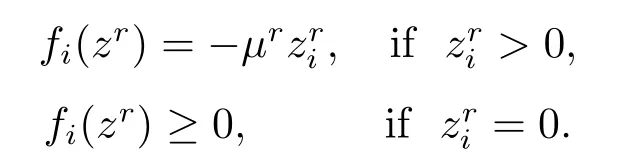
Definition 2.2[15]Givend >0,let{zr} ⊂Rn+be a set of points,{zr} is defined as ad-orientation sequence of the functionfif‖zr‖→∞asr→∞,and for eachzrthere exists a scalarµr >0 satisfying
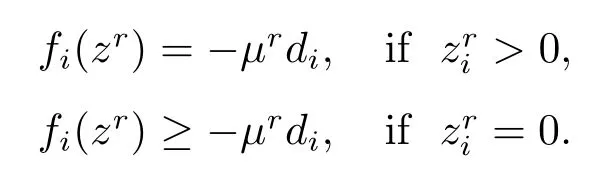
Remark 2.1Definition 2.2 is quite different from Definition 2.1.In the Definition 2.2,for eachzr >0,fi(zr)=−µrdifor some scalarµr,that is to say,all the vectorsf(zr) withzr >0 have the same direction−d.
In the sequel,we shall present a new concept of a generalized exceptional family of elements as follows.
Definition 2.3Givend>0,let{zr}⊂Rn+be a set of points,{zr}is called a generalized exceptional family of elements for the functionfif‖zr‖→∞asr→∞,and for eachzrthere exists a positive numberµrand a numberθ∈[0,1]such that
Remark 2.2In the above definition,ifθ=0,it reduces to the exceptional family of elements for the function[3].Ifθ=1,it becomes to thed-orientation sequence for the function[15].Therefore it is a generalization of the concepts of exceptional family of elements andd-orientation sequence for the functionf.
We all know that VI(K,f) is to find a solutionz∗satisfying
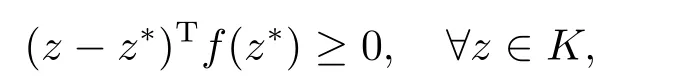
whereK ⊆Rnis closed and convex.In particular,when the setK=Rn+={z∈Rn:z≥0},VI(K,f) reduces to CP(1.1).
For a given positive vectord∈Rn,let
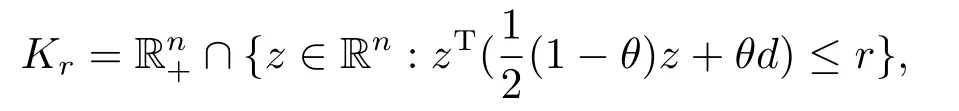
wherer >0 andθ∈[0,1].It is obvious thatKris bounded and convex,which implies that VI(K,f) has at least one solution[1].
In order to get a general existence theorem of CP(1.1),it is necessary to give the following lemma which is similar to the one in [15].
Lemma 2.1Givend>0,letf:Rn→Rnbe continuous,then CP(1.1) has a solution if and only if there exists a scalarr >0 andθ∈[0,1]such that VI(Kr,f) has a solutionzrwith (zr)T
ProofIfz∗is a solution to CP(1.1),then
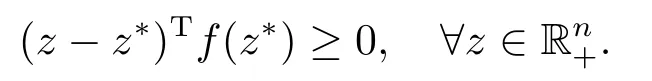
Letr >It is clear that
We can conclude from the definition of VI(Kr,f)[15]thatz∗is a solution to VI(Kr,f).
Next suppose that there existsr >0 andθ∈[0,1]such that VI(Kr,f) has a solutionzrwith (zr)T((1−θ)zr+θd) To prove thatzris a solution to CP(1.1),it is necessary to prove that In fact,denote Taking into account that (zr)T((1−θ)zr+θd) which shows that (2.2) holds.Sozris a solution to CP(1.1). By utilizing the above lemma,we can obtain the following main result. Theorem 2.1Iff:Rn→Rnis continuous,then there exists either the generalized exceptional family of elements for the functionfor a solution to CP(1.1). ProofSuppose that there does not exist any solution for CP(1.1).For a given vectord>0,we shall prove that there exists the generalized exceptional family of elements for the functionf.In fact,it follows from Lemma 2.1 that there exists no solutionzrof VI(Kr,f)such that (zr)T((1−θ)zr+θd) Taking into accountzrbeing a solution of VI(Kr,f),we can get i.e.,zris the unique solution to the following convex programming where Slater’s constrained qualification is satisfied. Therefore the Karush Kuhn Tucker conditions must be satisfied atzr,i.e.,there exists a vectorλr∈Rn+and a nonnegative scalarµrsuch that Take into accountzrbeing a solution of VI(Kr,f)and(zr)T((1−θ)zr+θd)=r.It is obvious that (2.5) and (2.6) hold.Thus,from the above conditions,we can conclude the following result which implies that The next object is to show thatµr >0.In fact,ifµr=0,then the above two relations reduce to which implies thatzris a solution to CP(1.1).This contradicts the assumption of the proof.Taking into account the fact thatd>0 and{zr}⊂Rn+,we have(zr)T((1−θ)zr+θd)=rand‖zr‖→+∞asr→+∞.By Definition 2.3,we get that{zr} is the generalized exceptional family of elements for the functionf.The proof is complete. The following result is a direct consequence of Theorem 2.1. Corollary 2.1If there exists no generalized exceptional family of elements for the functionf,then CP (1.1) has a solution. In this section,we shall show that Karamardian type condition,Isac and Gowda type condition orp-order generalized coercivity type condition is the sufficient condition for the existence of solutions to CP(1.1),respectively.Finally applying the new concept to theP∗-mapping CP,we also present a new existence result. Firstly,we shall give an existence theorem related to the Karamardian type condition for CP(1.1). Theorem 3.1Letfbe a function satisfying the Karamardian type condition,i.e.,there exists a compact convex setD ⊂Rn+such that for everyz∈Rn+D,there existsy∈Dsatisfying (z−y)Tf(z)≥0.Then there exists no generalized exceptional family of elements for the functionfand consequently CP(1.1) has a solution. ProofSuppose that there exists the generalized exceptional family of elements{zr}forf.We shall prove thatfdoes not satisfy the Karamardian type condition on Rn+,that is to say,we shall show that for every compact convex setD ⊂Rn+,there exists a positive scalarrsuch thatzr∈Rn+Dand (zr−y)Tf(zr)<0 for eachy∈D. Ifzri >0,from the first condition of Definition 2.3,for a given vectord>0,we can get Ifzri=0,from the second condition of Definition 2.3,for a given vectord>0,one has Therefore Take into accountDbeing compact.There exists some positive scalarcsuch thatyTd≤cfor everyy∈D.Since‖zr‖→+∞,we have which implies that the Karamardian type condition on Rn+does not hold.This contradicts the assumption of the theorem. In the following,we shall provide the Isac and Gowda type sufficient condition for the existence of a solution to CP(1.1). Definition 3.1[16]We say thatϕ:Rn→Rnis monotone decreasing with respect to Rn+if there exists a positive scalart0such that for everyz∈Rn+and everys,twiths≥t≥t0,we obtain We present the following lemma in order to show the nonexistence of the exceptional families of elements for the monotone decreasing function. Lemma 3.1[17]ϕis monotone decreasing with respect to Rn+if and only if for everyα≥1 and everyz∈Rn+,we get Theorem 3.2Letfbe a function satisfying the Isac and Gowda type condition,i.e.,there exists a scalarp≥1 such thatϕ(z)=‖z‖p−1z−f(z) is monotone decreasing with respect to Rn+.Then there does not exist the generalized exceptional family of elements for the functionf.Hence CP (1.1) has a solution. ProofSuppose that there exists the generalized exceptional family of elements{zr}for the functionf.Sinceϕ(z)=‖z‖p−1z−f(z) is monotone decreasing with respect to Rn+,we can obtain from Lemma 3.1 that for everyα≥1 and everyz∈Rn+, In view of the fact‖zr‖→+∞asr→+∞,we can conclude that there exists a scalarr0>0 such that for allr≥r0,‖zr‖≥1 holds.Lettingα=‖zr‖andz=in (3.1),one gets i.e., Noting the fact that for a given vectord >0,{zr} is the generalized exceptional family of elements for the functionf,we obtain from Definition 2.3 whereI+={i:zri >0}.Combining the above equation and (3.2),one can get Thus Becausefis a continuous function andϕ(z) is bounded onB(0,1)={z:‖z‖≤1},there exists some positive scalarMsuch that This shows that This is a contradiction. The sufficient condition related top-order generalized coercivity is presented as follows for the existence theorem of a solution to CP(1.1). Theorem 3.3Letfbe ap-order generalized coercive function,i.e.,there exists∈Rn+andp∈(−∞,1]such that for each sequence{zα}⊂Rn+with‖zα‖→+∞, Then there does not exist the generalized exceptional family of elements for the functionfand consequently CP(1.1) has a solution. ProofSuppose that{zr} is the generalized exceptional family of elements for the functionf.From Definition 2.3,for a given vectord>0,we have that for anyp∈(−∞,1],which shows thatfcan not be ap-order generalized coercive function.This is a contradiction. The above results imply that these conditions provide some new existence results of CP(1.1).However,these are not necessary in general.A natural question is whether there exists a necessary and sufficient condition for the existence result of solution to CP(1.1).The following result will give a positive answer. Theorem 3.4Letfbe a pseudo-monotone mapping,i.e.,for each different pointz,y∈Rn, Then CP(1.1) has a solution if and only if there exists no generalized exceptional family of elements for the functionf. ProofIn view of Corollary 2.1,we only need to prove that if CP(1.1) has a solution,then there exists no generalized exceptional family of elements.Letz∗be a solution for CP(1.1),i.e., which is equivalent to Taking into accountfbeing pseudo-monotone,one can get Assuming that there exists the generalized exceptional family of elements{zr}for the functionf,we have the following inequality from Definition 2.3,for a given vectord>0, Since‖zr‖→+∞asr→+∞,the above inequality implies that for sufficiently larger, which is in contradiction with (3.3). The linearP∗mapping was first defined by Kojima et al.[18]Since then,CP(1.1) withP∗mapping has been applied extensively to interior point algorithm.In the following,by using the new concept of generalized exceptional family of elements,we shall prove that CP(1.1)withP∗mapping has a solution under the strictly feasible condition. Definition 3.2[18]For a mappingf:Rn→Rn,fis defined as aP∗mapping if there exists a constantγ≥0 such that for any distinctz,y∈Rn, holds,whereI+(z,y,f)={j:(zj−yj)(fj(z)−fj(y))≥0}. Remark 3.1Denote then (3.4) can be converted into whereI−(z,y,f)={j:(zj−yj)(fj(z)−fj(y))<0}. It is clear that a monotone mapping is aP∗mapping.Now,we can obtain the following result. Theorem 3.5Letf:Rn→Rnbe a givenP∗mapping.If there existsu∈Rn+such thatf(u)>0,then there does not exist the generalized exceptional family of elements for the functionf.Hence the corresponding CP has a solution. ProofSuppose that{zr}is the generalized exceptional family of elements for a functionf.From Definition 2.3,for a given vectord>0,we have that i.e.,we have In view of the fact that‖zr‖→+∞,it is obvious that there exists at least one component indexi0such thatzi0→+∞asr→+∞.Therefore,we can obtain that which shows thatI−(z,y,f) is not an empty-set.Thus,I+(z,y,f) is not an empty-set from Definition 3.2.This implies that there exists a sequence{zrj}⊂{zr}such that for some fixed indexp,qand all the sequence{zrj} and hold.In view of the fact thatfis aP∗mapping,by (3.7) (3.8) and Definition 3.2,we can get Suppose that,then This is a contradiction with (3.8).Therefore,we conclude that 0. If=0,we can get that If 0,we have Thus,(3.9) can be rewritten as follows, i.e., In view of the fact that+∞,thus,for sufficiently largerj,the left side of the above formular is negative,which is a contradiction to the fact that the right side of the above inequality tends tofi0(u)>0. We presented a new concept of exceptional family of elements,which is a generalization for the concept ofd-orientation sequence and exceptional family of elements for a continuous function.We have proved that if there exists no generalized exceptional family for a continuous function,then CP(1.1) has a solution.It is also shown that a continuous function does not possess the generalized exceptional family under the Karamardian type condition,the Isac and Gowda type condition orp-order generalized coercive type condition,respectively.By applying the new concept to theP∗-mapping CP,we have obtained a new existence result.
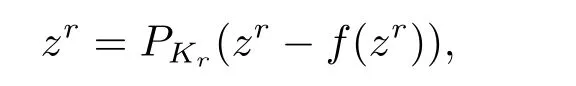
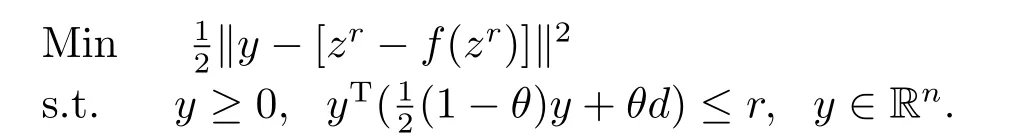
3.Existence Conditions of Solution to CP
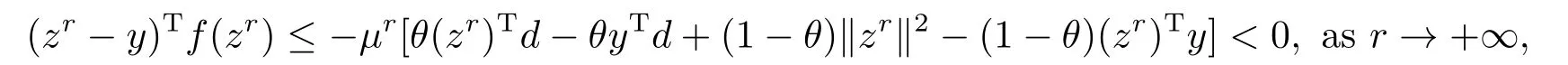
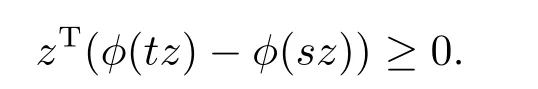
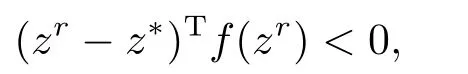
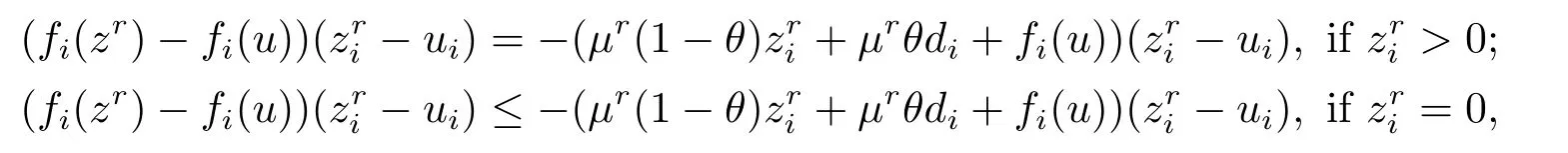
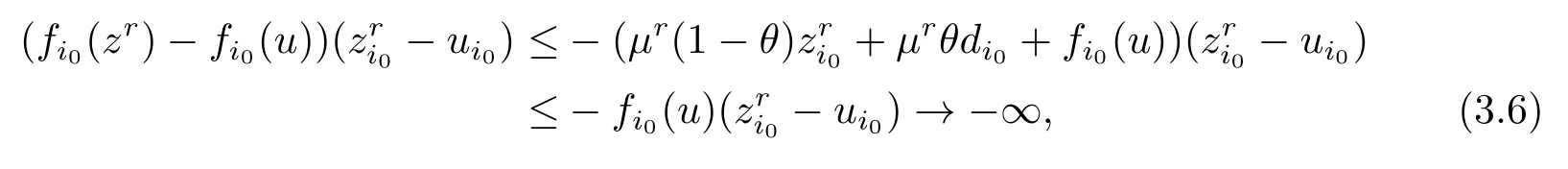
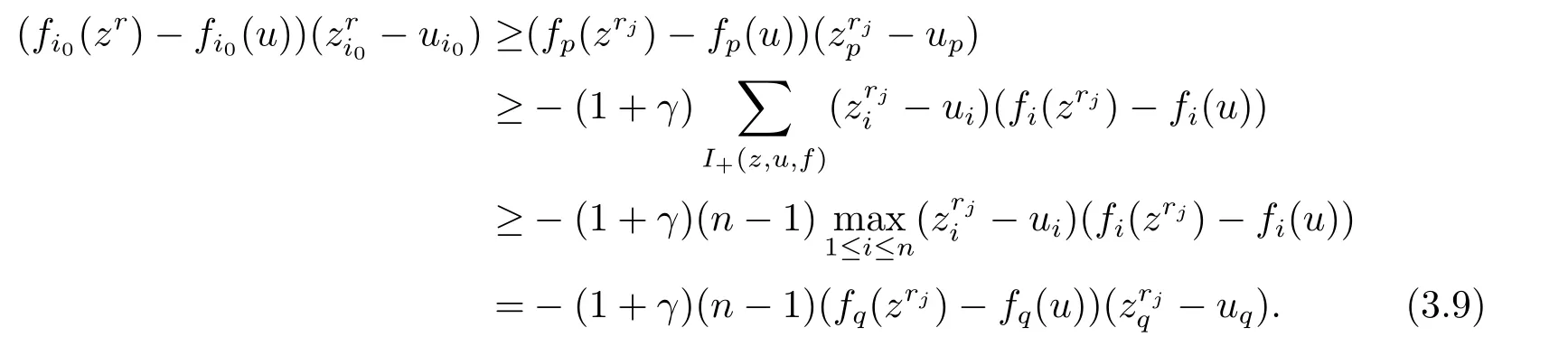
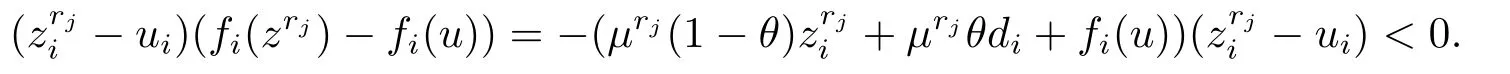
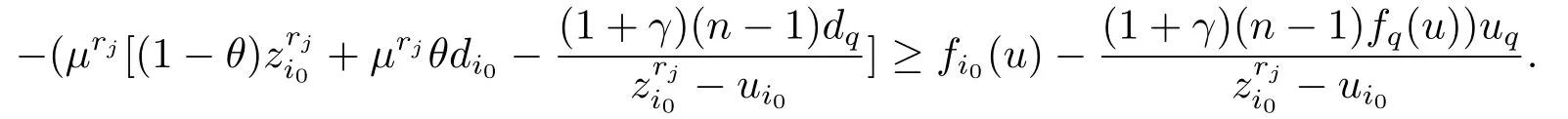
4.Conclusions
