2-维Ginzburg-Landau方程的一种混合有限元方法的高精度分析
2019-10-16李庆富王俊俊
李庆富,王俊俊
( 平顶山学院数学与统计学院,河南 平顶山467000)
1.引言
考虑如下2维Ginzburg-Landau方程:

其中Ω ⊂R2是一个边界为∂Ω的矩形,0 非线性Ginzburg-Landau方程的有限元方法被很多学者专家所关注.例如,文[1-2]研究了一个非线性耦合形式的Ginzburg-Landau方程,其中文[1]研究了其半离散和隐式Euler全离散格式,文[2]提出了一种线性化的CN格式,二者都得到了最优误差估计.文[3]给出了(1.1)有限差分的收敛结果,避开了数值解的估计,利用数学归纳法证明了其格式在L2(Ω)-模下的误差估计.文[4]针对(1.1)给出了三种线性化的差分格式,接着研究了该方程的平面波解,并得到了三个格式的截断误差. 混合有限元方法虽然对空间要求光滑度较低,并能同时得到原始变量和中间变量数值解等优势,但需要满足所谓的LBB条件,这通常不是一件容易的事.为了降低空间选取的难度,文[5]对二阶椭圆问题提出了另一种混合元格式.较传统的混合元格式具有以下特点:当空间满足一个简单的包含关系时离散的LBB条件自动满足,自由度少且可避免对矢量有限空间的试探函数进行散度运算等.因此,该格式已被广泛应用在各种方程中[6−10]. 本文借用文[5-10]的思想,使用五节点元[11−12]及零阶Raviart-Thomas元讨论了2-维Ginzburg-Landau方程的一种新混合有限元方法.首先给出其半离散的有限元格式,证明了其解的存在唯一性,利用导数转移等技巧得到了其在半离散下的超逼近结果.其次,给出了其一个线性化的Euler格式,有技巧的导出了原始变量u在H1模意义下及流量在L2模意义下的O(h2+τ2)阶的超逼近性质.最后利用一个数值算例验证了理论结果. 令Ω是一个矩形,Γh是Ω的一个正则剖分.对于一个给定的Kh∈Γh,记四个顶点和四条边分别为ai,i=1∼4 和li=i=1∼4 (mod 4).相对应的有限元空间分别定义为Vh和: 其中,Qij=span{xrys,0≤r≤i,0≤s≤j}.[vh]表示跨过单元边界F的跳跃值,当F ⊂∂Ω时,容易验证,是Vh上的模.对于u∈H1(Ω),(H1(Ω))2,设Ih:H1(Ω)→Vh和Πh:(H1(Ω))2分别为由Vh和上诱导的插值算子,满足:Ih|K=IK,Πh|K=ΠK及 和 其中是对应边li(i=1,2,3,4)的单位外法向量.有以下引理:. 引理2.1[12]对于任意的(H2(Ω))2,有 令=∇u,则(1.1) 相对应的弱形式是寻找使得 定理3.1问题(3.1) 存在唯一解. 证设和分别为Vh和上的基,则有 其中 由于B是正定矩阵,则对t∈(0,T],(3.1) 存在唯一解. 令 假设(⋆)‖uh‖0,∞<1. 定理3.2令u和uh分别为(1.1) 和(3.1) 的解,若u∈H3(Ω),(H2(Ω))2,我们有 证由(3.1)和(1.1)我们有误差方程: 将其改写为 在(3.6)的第一式中令=∇ξt,在第二式中令vh=ξt,两式相加,取其实部有 显然有 由假设得到 利用导数转移以及文[12]的结论有 综合以上误差,代入(3.7)有 由于ξ(0)=0,两端关于t从0 到t做积分有 利用Gronwall不等式得到 则有 在(3.6)中令= 也即 最后需要说明先验假设(⋆)的正确性.首先,记δ(t)∇(u(t)−uh(t)).有初始逼近和插值理论可知‖δ(0)‖0,∞<1成立.由函数的连续性,在t=0的一个小领域[0,ε]内,定理3.2成立. 如果假设不再整个区间I=[0,T]上成立,设t0=inf{t:‖δ(t)‖0,∞≥1,t∈I},则有‖δ(t0)‖0,∞=1,t0>0(事实上,若‖δ(t0)‖0,∞>1,由函数的连续性,总可以找到一个点t1 由定理3.2的证明过程可以看出其结论在[0,t0]处成立,则由逆不等式,对于充分小的h,有‖δ(t)‖0,∞≤‖∇(u(t)−Ihu(t))‖0,∞+‖∇(Ihu(t)−uh(t))‖0,∞≤Ch‖u‖2,∞+Ch−1‖∇(Ihu(t)−uh(t))‖0≤Ch,t∈[0,t0].选择适当的h0,当h≤h0,有‖δ(t)‖0,∞≤Ch <1,t∈[0,t0].此与‖δ(t0)‖0,∞=1矛盾.所以先验假设(⋆)是正确的. 注3.1由于(3.7)左端没有关于‖ξt‖h的项存在,则在估计项ξt的时候,对(3.10)进行导数转移,将关于t的导数从ξ上转移到上,最终得到关于‖ξ‖h的估计. 令{tn:tn=nτ;0≤n≤N}是[0,T]上的均匀剖分,时间步长是τ=T/N,记σn=σ(X,tn),0≤n≤N,定义:利用[14]线性化的有限元方法,寻找使得当n≥1 时,有 令 定理4.1设和分别为(1.1)和(4.1)的解,对任意的m=1,2,...,N,若um∈H3(Ω),(H2(Ω))2,有 证得到误差方程 显然有 由文[13]的高精度结果可以看到 又由于 则有 也就是 另一方面,在(4.4)的第一个式子中,选取=有 因此,存在τ1,h1,C1,使得当τ≤τ1,有 由条件τ=O(h2)得到 其中h≤h2≤1/CC2. 假设(4.3)对于m≤n−1成立,由于τ=O(h2),则存在h3,有 其中h≤h3=1/CC0. 下面我们证明结果对于m=n也成立.由(1.1)和(4.1), 将其变形后有 类似ξ1的证明有 改写B4,再估计有 总结以上的误差结果,对(4.8)从2到n求和,则有 利用离散的Gronwall不等式,有 又由于令= 则存在τ4,h5,C4,使得当τ≤τ4有 由条件τ=O(h2),也有 其中h≤h5≤1/CC4.可以看到C4和没有任何关系,当取和则(4.15) 对m=n成立.至此数学归纳法结束,定理证毕. 注4.1由于文中采用了线性化的全离散格式,当时时刻的时间层分析需要用到上一时刻时间层的结论,因此选择数学归纳法进行证明.为了每一个时间层的结果到最后都应该由一个统一的系数来控制,在证明第n层结果时,需要利用(4.7),而不能直接利用带有C0的归纳假设结果. 注4.2由于(4.8)左端没有关于的项,则对于B3来说,直接估计就会降低最后结果的阶,利用一个分列技巧将τ从内积的一端转向另一端,回避出现项,从而得到最后结果. 在这一章里,给出一个算例来验证理论部分.考虑(1.1),其中,Ω=[0,1]×[0,1],a1=a2=b1=b2=1,真解为u=etxy(1−x)(1−y).在表格5.1-5.8中,选择τ=5h时刻t=0.25,0.5,0.75,1.0 来分别验证试验结果.可以看到当h→0时,有最优估计阶O(h),最优估计阶O(h2),可以看到所有结果验证了前面理论部分. 表5.1 数值解Unh 在t=0.25的结果 表5.2 数值解Unh 在t=0.5的结果 表5.3 数值解Unh 在t=0.75的结果 表5.4 数值解Unh 在t=1.0的结果 表5.5 数值解在t=0.25的结果 表5.5 数值解在t=0.25的结果 m×mpn−Pnh ‖H(div;Ω) 阶 ‖Πhimages/BZ_89_748_1642_782_1686.pngn−Pnh ‖0 阶4×4 0.03378079483080 — 0.00748816766348 —8×8 0.01698575787882 0.9919 0.00191969829692 1.9637 16×16 0.00850227630890 0.9984 0.00048302136361 1.9907 表5.6 数值解 在t=0.5的结果 表5.6 数值解 在t=0.5的结果 m×m ‖pn−Pnh ‖H(div;Ω) 阶 ‖Πhimages/BZ_89_748_1642_782_1686.pngn−Pnh ‖0 阶4×4 0.03376858013758 — 0.00743287024398 —8×8 0.01698605210408 0.9913 0.00192229990270 1.9511 16×16 0.00850236919353 0.9984 0.00048465359581 1.9878 表5.7 数值解在t=0.75的结果 表5.7 数值解在t=0.75的结果 m×m ‖pn−Pnh ‖H(div;Ω) 阶 ‖Πhimages/BZ_89_748_1642_782_1686.pngn−Pnh ‖0 阶4×4 0.03376851491266 — 0.00743257391232 —8×8 0.01698603311508 0.9913 0.00192213210266 1.9512 16×16 0.00850236757636 0.9984 0.00048462522470 1.9878 表5.8 数值解在t=1.0的结果 表5.8 数值解在t=1.0的结果 m×m ‖pn−Pnh ‖H(div;Ω) 阶 ‖Πhimages/BZ_89_748_1642_782_1686.pngn−Pnh ‖0 阶4×4 0.03376851775874 — 0.00743258684292 —8×8 0.01698603303400 0.9913 0.00192213138609 1.9512 16×16 0.00850236755676 0.9984 0.00048462488080 1.98782.单元介绍





3.半离散超逼近结果
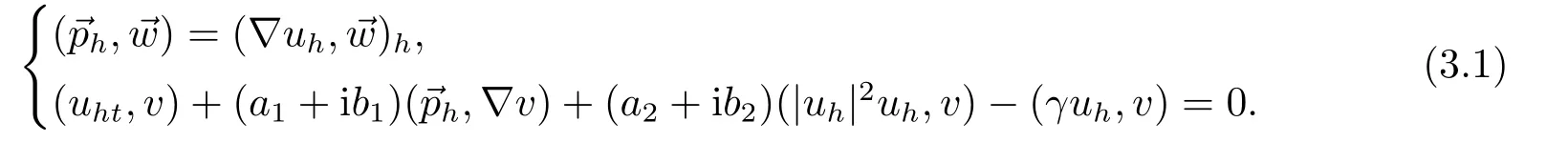





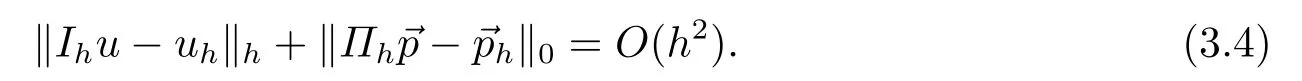
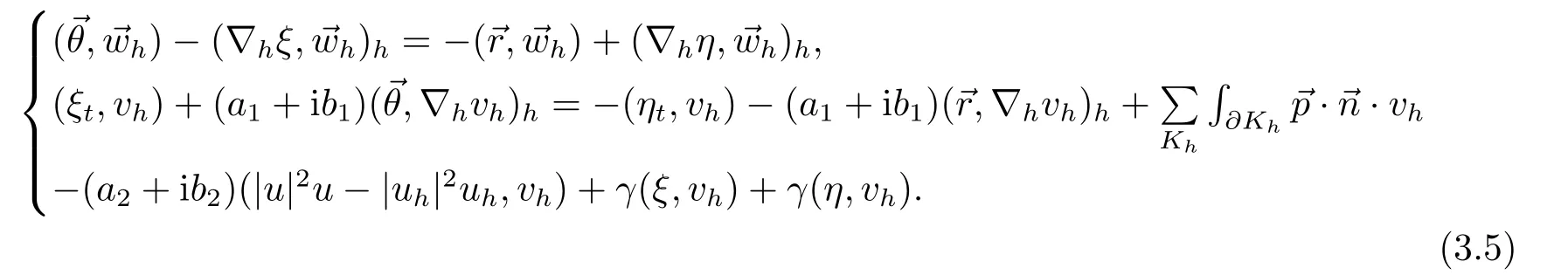






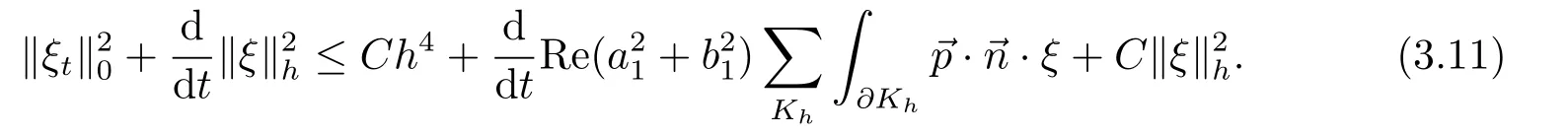





4.线性化逼近格式

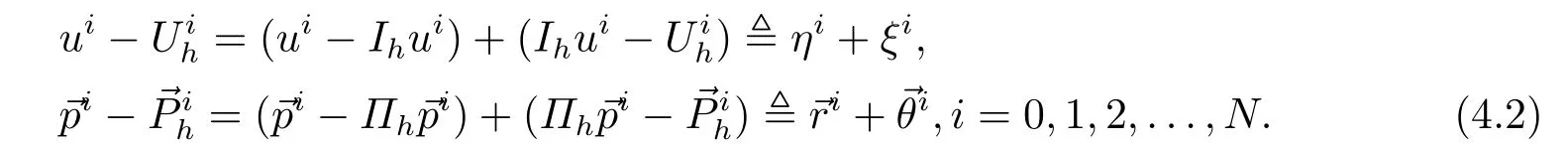





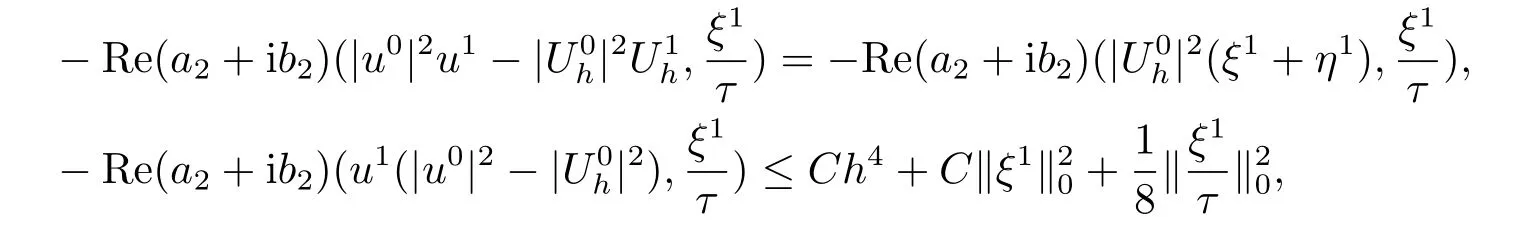
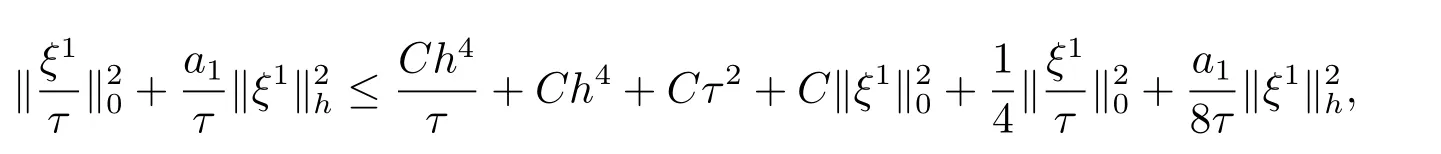

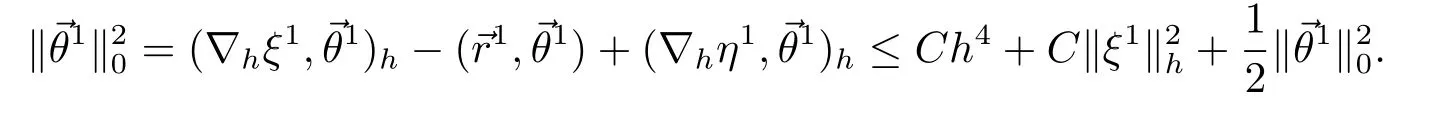







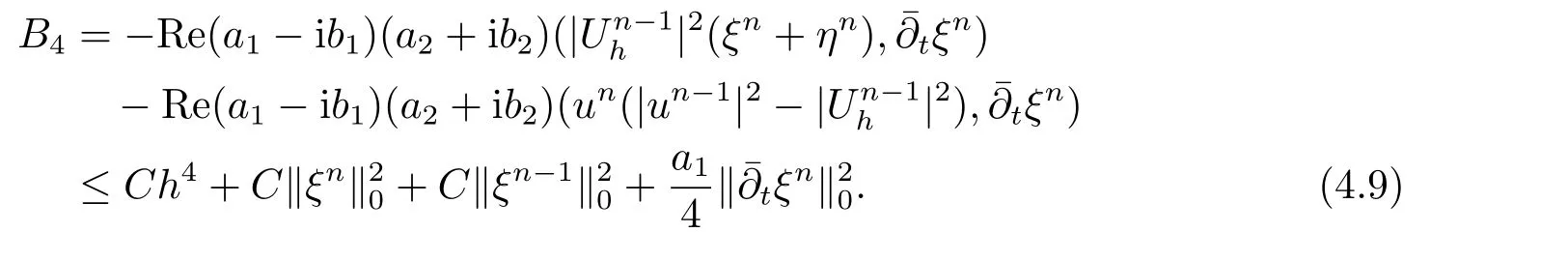



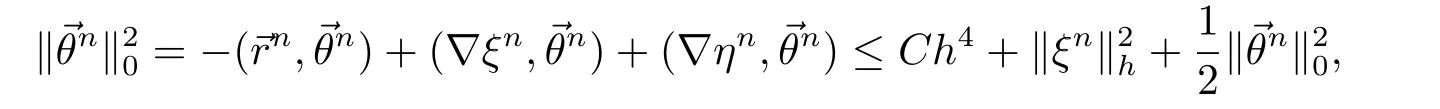


5.数值算例








猜你喜欢
杂志排行
应用数学的其它文章
- 凸二次半定规划一个新的原始对偶路径跟踪算法
- Numerical Solution of Nonlinear Stochastic Itô-Volterra Integral Equations by Block Pulse Functions
- 面板数据分位数回归模型的工具变量估计
- Stability Analysis of Indirect Adaptive Tracking Systems for Simple Linear Plants with Unknown Control Direction
- The Boundedness of Maximal Dyadic Derivative Operator on Dyadic Martingale Hardy Space with Variable Exponents
- Positive Solutions for Kirchhoff-Type Equations with an Asymptotically Nonlinearity
