一阶非自治共振系统周期解的存在性
2019-10-16陈瑞鹏李小亚
陈瑞鹏,李小亚
( 北方民族大学数学与信息科学学院,宁夏 银川750021)
1.引言与主要结果
近年来,非线性微分方程

周期解的存在性被诸多学者深入研究,其中a,b∈C(R,[0,∞))为ω-周期函数且满足
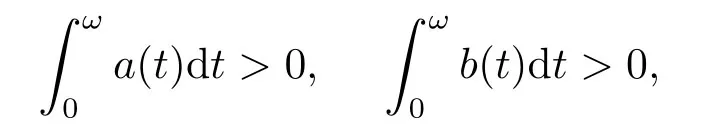
τ是一个ω-周期连续函数,λ为正参数.注意到当λ=0时,方程(1.1)将退化为u′=−a(t)u,这恰为经典的马尔萨斯人口模型.在现实世界应用中,方程(1.1)主要用于描述与呼吸、心律失常及血细胞生成等密切相关的多种人体生理过程,相关研究成果见文[1-10]及其参考文献.同时,诸多学者致力于研究(1.1)相应的微分系统,例如[11-13]等.特别地,文[12]讨论了系统
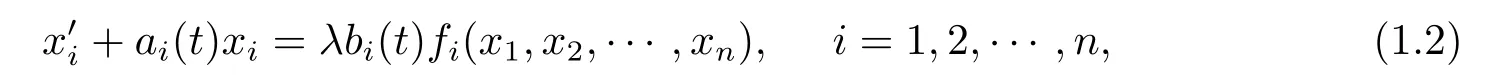
注意到基本假设∫ω0ai(t)dt>0通常用于保证线性微分方程

是非共振的,该假设在上述所涉及文献的讨论中起到了关键作用.事实上,在非共振情形下,能够运用不动点理论、分歧理论等经典工具研究相应问题并建立存在性结果.这里称线性方程(1.3)为非共振的,若它的唯一解是平凡解.假设h是一个L1-函数,当线性方程(1.3)非共振时,由著名的Fredholm二择一定理可知非齐次问题存在唯一解,且可表示为

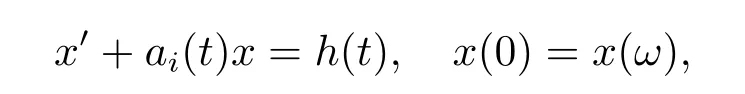
其中G(t,s)为(1.3)相应的Green函数,参见文[7-13]等.
显然,大多数学者主要研究非共振问题.相比较而言,对于共振系统和方程的研究进展十分缓慢,而且关于共振系统周期解的存在性结果极少.对于共振情形下非线性微分方程的其它研究工作,可见文[14-17]等.于是,一个自然而有趣的问题是:当
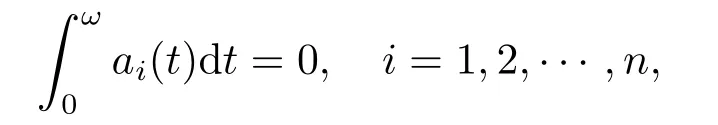
时,方程(1.1)相应的微分系统是否仍存在周期解? 本文将为非自治共振系统

建立新的周期解存在性定理,从而为该问题给予肯定的回答.此处称向量函数(u(t),v(t)),t∈R,为系统(1.4)的一个周期解,若u(t)=u(t+ω),v(t)=v(t+ω),u=u(t),v=v(t)∈C1[0,ω]且满足(1.4).据我们所知,上述问题迄今未曾被研究过,本文所得结果将填补这个空白.
本文总假设:
(H1)f,g∈C(R×R×R,R)有界且关于t是ω-周期的.此外,存在正常数l1和l2,使得对任意的(t,x,y)∈R×R×R,

(H2)pi,ci∈C(R,R)是ω-周期函数且满足ci(t)dt=0,i=1,2.
注1.1(H2)蕴含了函数ci的平均值满足
在上述基本假设下,本文的主要结论是:
定理1.1假设(H1)和(H2)成立.若p1(t)≡0,p2(t)≡0,则系统(1.4)至少存在一个周期解.
注1.2由条件p1(t)≡0,p2(t)≡0可得∫(t)dt=0 (i=1,2),从而本文所研究的微分系统(1.4)是共振系统.
引理1.1[18]令

其中Rn是通常的n-维欧式空间,其范数为假设映射F=(f1,f2,···,fn):Rn在G的闭包G上连续,对G的边界∂G上的元素x成立F(x)≠θ=(0,0,···,0),并且
(i)fi(x1,x2,···,xi−1,−L,xi+1,···,xn)≥0,1≤i≤n;
(ii)fi(x1,x2,···,xi−1,+L,xi+1,···,xn)≤0,1≤i≤n.
则F(x)=θ在G中存在一个解.
本文结构作如下安排:在第二部分我们将证明定理1.1,并给出具体的例子来阐释本文的主要结果;在第三部分我们将给出一些相关结果和注记.
2.主要结果的证明
方便起见,首先给出一些符号和定义.
定义线性微分算子Li:D(Li)→E,

其中E=C[0,ω]是一个Banach空间,范数为且
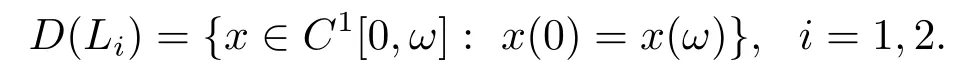
因为Ker(Li)={c},c∈R,所以算子Li不可逆.进一步,令Lx:=x′,则由p1(t)≡0,p2(t)≡0可得
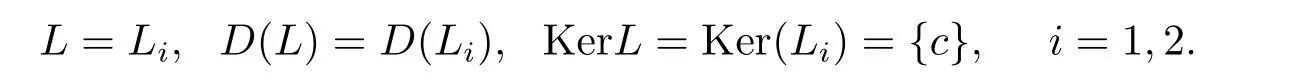
定理1.1的证明令V=KerL,则其中

于是,u和v可重写为

由假设(H2)可知(u,v)是系统(1.4)的一个周期解当且仅当(u,v)满足下列方程

由(2.1)和(2.3)分别可得
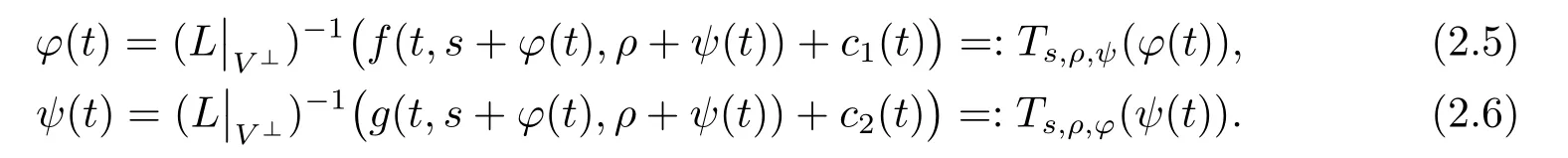
进一步,假设(H1)保证了存在常数M1>0,M2>0,使得
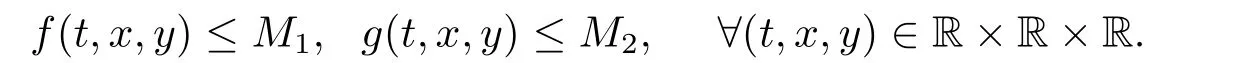
据此并直接应用Schauder不动点定理[19],不难证明对任意的s和ρ,方程(2.5)和(2.6)均存在不动点.假设对于s=s∗,ρ=ρ∗,方程(2.5)和(2.6)分别有不动点和,这里s∗与ρ∗是某些待定常数.此外,容易看到(2.5)的每个可能的解φ是有界的,因而存在常数R1>0,使得对满足(2.5)的φ成立‖φ‖≤R1.同理,存在常数R2>0,使得(2.6)的任一可能解ψ满足‖ψ‖≤R2.

则本定理的证明将完成.事实上,可取充分大的正常数s1,使得s1+≥l1>0,进一步由假设(H1)可知

另一方面,存在绝对值充分大的常数s2<0,使得s2+≤−l1<0,从而

类似地,可选取常数ρ1>0和ρ2<0,它们满足ρ1与|ρ2|充分大,且使得
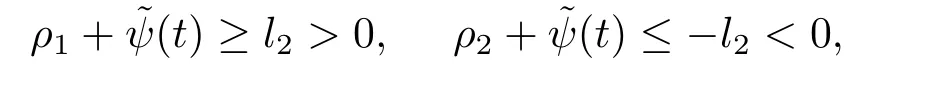
相应地,可得

令
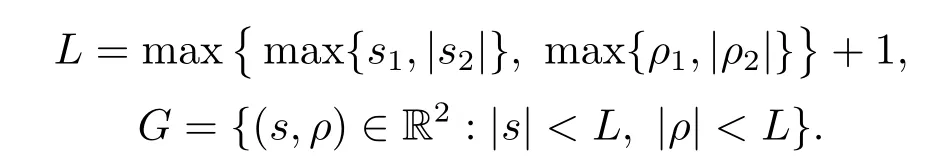
定义

则由假设(H1)易知F:=(F1,F2):R2在上连续.此外,结合(2.9)-(2.12)及G的定义,不难验证F((s,ρ))≠θ=(0,0),∀(s,ρ)∈∂G.
下面,我们将证明引理1.1的条件(i)和(ii)满足.首先,若能够证明

与
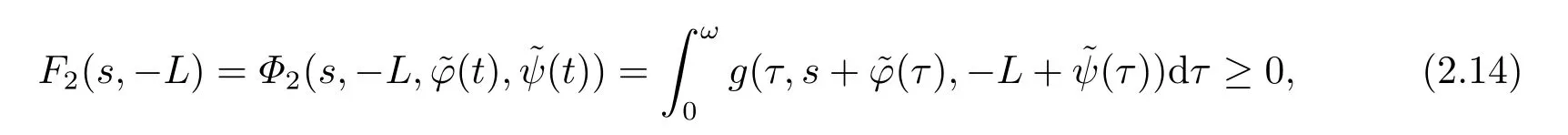
则引理1.1的条件(i)必满足.事实上,由算子L的定义可知−L+≤s2+≤−l1,这结合假设(H1)中的第一个不等式表明(2.13)成立.进一步,假设(H1)及−L+≤ρ2+≤−l2保证了(2.14)亦满足.通过类似讨论可得

于是,引理1.1的条件(ii)亦成立.
最后,由引理1.1可知存在(s0,ρ0)∈G,使得F((s0,ρ0))=θ,因而(2.7)和(2.8)成立.令s∗=s0,ρ∗=ρ0,则定理1.1证毕.
例2.1考虑非自治共振系统
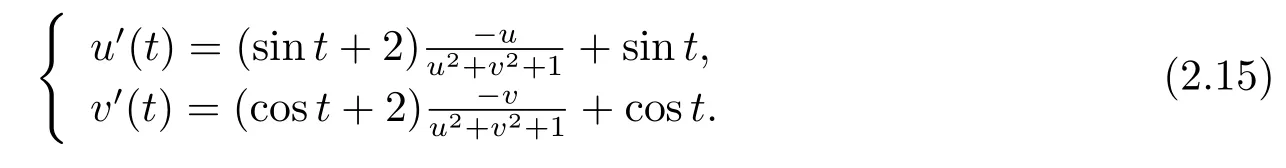
显然,

c1(t)=sint,c2(t)=cost是关于t的2π-周期连续函数,且满足

因此,假设(H2)满足.
另一方面,f(t,u,v):=于R3上连续且关于变量t是2π-周期的.进一步,不难验证
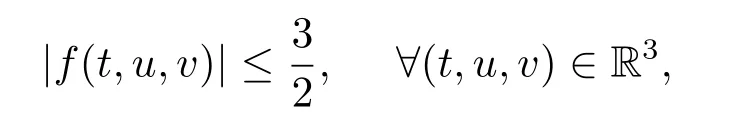
并且对任意正常数l1,有

于是,f(t,u,v)满足假设(H1).同理可知

亦满足假设(H1).从而由定理1.1可知系统(2.15)至少存在一个周期解.
注2.1显然,非自治共振系统(2.15)并不能由文[5-13]等所采用的研究方法处理,而且上述存在性结果是新颖的.
3.相关结果与注记
本节将给出一些相关结果和注记.
推论3.1假设(H1)和(H2)成立.若

则系统

至少存在一个周期解.
证类似于定理1.1的证明,易知结论成立.
考虑如下n×n系统

假设:
(H1)′fi∈C(R×Rn,R)有界,且关于变量t为ω-周期.存在正常数li,使得对任意(t,x1,x2,···,xn)∈R×Rn,有

(H2)′ pi,ci∈C(R,R)是ω-周期函数且满足
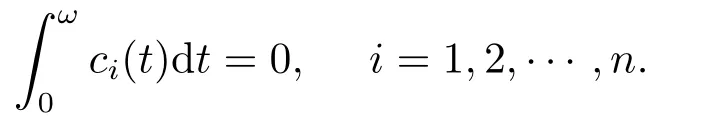
定理3.1假设(H1)′和(H2)′成立.若pi(t)≡0 (i=1,2,···,n),则系统(3.1)至少存在一个周期解.
证通过与定理1.1证明中类似的讨论,可证结论成立.
注3.1需要指出的是对于特殊情形

定理3.1 的结论仍成立.
注3.2本文并未讨论pi(t)0但0pi(t)dt=0 (i=1,2,···,n)的情形,然而我们相信定理1.1的证明方法完全可以用来处理此情形.此外,虽然本文主要讨论时滞函数τ(t)≡0的情形,但是定理1.1的证明方法对于τ(t)0的系统仍适用.
猜你喜欢
杂志排行
应用数学的其它文章
- 凸二次半定规划一个新的原始对偶路径跟踪算法
- Numerical Solution of Nonlinear Stochastic Itô-Volterra Integral Equations by Block Pulse Functions
- 面板数据分位数回归模型的工具变量估计
- Stability Analysis of Indirect Adaptive Tracking Systems for Simple Linear Plants with Unknown Control Direction
- The Boundedness of Maximal Dyadic Derivative Operator on Dyadic Martingale Hardy Space with Variable Exponents
- Positive Solutions for Kirchhoff-Type Equations with an Asymptotically Nonlinearity
