埋地管道缺陷的自漏磁场计算方法研究*
2019-10-16李忠吉李长俊成婷婷张财功
李忠吉,李长俊,成婷婷,张财功
(西南石油大学 石油与天然气工程学院,四川 成都 610500)
0 引言
埋地管道由于环境恶劣、机械损伤以及其他意外荷载的影响,可能会产生凹陷、裂纹等缺陷,一旦缺陷恶化导致管道破裂,就会造成管道中的介质泄漏,污染环境并且易造成安全事故[1-3]。因此,定期对埋地管道进行检测,尽早发现管道形成的缺陷、判断缺陷特征以及消除缺陷,对管道的安全运行十分重要。
实际工程应用中,传统的漏磁检测、超声波检测等无损检测方法存在着设备复杂,检测条件受限等缺点,针对这些检测技术的不足,Dubov在1997年首次提出的金属磁记忆检测方法有效地解决了这些问题[4]。这种方法的基本原理可以总结为:在地磁场的影响下,应力和应变会使铁磁材料微结构中的磁畴取向发生不可逆的变化,使得应力集中的上方出现自漏磁场[5],通过磁力计检测漏磁场变化,即可确定构件应力集中位置[6]。
目前磁记忆检测主要用磁力梯度仪等仪器检测缺陷可能存在的位置,并不能对缺陷进行准确量化,主要是因为自漏磁场形态与缺陷形式,自漏磁场大小与缺陷大小之间的对应关系还未完全明确[7]。
针对这些热点问题,Mandache等[8]建立了圆柱形缺陷的表面磁场计算模型,突破了缺陷形状对模型的限制;Xu等[9]应用磁荷理论建立了材料内部缺陷的自漏磁场计算模型;Li等[10]基于磁偶极子理论和J-A磁化模型建立了埋地管道缺陷的自漏磁场计算模型,并对影响自漏磁场的缺陷参数进行了分析;黄作英等[11]应用双极磁荷法分析了3种缺陷类型的径向磁场和轴向磁场。虽然国内外学者已经建立了一些缺陷与自漏磁场之间的定量模型,但由于没有考虑到缺陷处磁荷分布的不均匀性,导致计算的自漏磁场与实际数据存在较大的差异,从而难以准确判断缺陷的特征。
基于此,本文考虑缺陷处磁荷实际分布,提出新的埋地管道缺陷自漏磁场计算方法,并将其应用在某埋地管道磁记忆检测中,以期为提高管道缺陷量化的准确性提供理论参考。
1 力磁关系
材料缺陷处磁荷的分布取决于材料的磁化强度,而材料磁化的强弱又与作用在材料上的应力有关,因此首先需要研究材料的力磁关系。对于油气管道这类铁磁材料,已经提出了一些力磁耦合模型,Jiles等[12]基于耦合理论和趋近原理,引入有效场,将应力的影响等效为外磁场的作用:
Heff=H+αM+Hσ
(1)
(2)
式中:Heff为总的磁场强度,A/m;H为地磁场强度,A/m;α为域间耦合的平均场参数,由实验确定;M为磁化强度,A/m;Hσ为应力作用下的等效磁场强度,A/m;σ为作用在材料上的应力,Pa;μ0为真空磁导率,T·m/A;λ为磁致伸缩系数;θ为应力与外磁场的夹角,(°);ν为泊松比。
材料在应力作用下的磁化包括可逆和不可逆2部分,在模型的建立过程中须分别计算。基于能量最小原理,最终推导出应力和磁化强度的关系如下:
(3)
(4)
式中:Man为材料非磁滞磁化强度,A/m;Ms表示材料饱和磁化强度,A/m;ε,c和a均表示材料磁化特性的参数。
根据上述的应力磁化模型,经过迭代计算即可求得材料在应力作用下的磁化强度。
2 自漏磁场计算模型的建立
埋地管道缺陷自漏磁场形成示意如图1所示。以埋地管道表面常见的长方体凹槽缺陷为例,长宽深分别为a,b,c,以缺陷中心为原点,建立图1中的坐标系。根据磁偶极子理论,在地磁场的作用下,管道出现缺陷时,缺陷的侧壁将会积累正负磁荷,自漏磁场便由这些正负磁荷形成的磁场叠加而成[13]。

图1 埋地管道缺陷自漏磁场形成示意Fig.1 Schematic diagram for self-leakage magnetic field formation of buried pipeline defect
通过管道力磁关系可知,缺陷磁荷分布情况与缺陷处的磁化强度有关,但是缺陷处的应力不连续,使得其磁化强度的分布也具有不连续性,因此不能用1个连续的函数来表达。为了精确地计算出缺陷处的磁化强度,本文利用ANSYS 16.0 Workbench的强大非线性分析功能,对管道进行网格离散,导出缺陷表面处若干微小单元的应力,再计算得到缺陷表面处每个单元的磁化强度。
以图1中缺陷面3为例,采用具有较强适应性的四面体网格进行划分,沿z轴划分成n个网格,记为i=1,2,3,,n;沿y轴划分成m个网格,记为j=1,2,3,,m,则缺陷面3共被划分成n×m个单元格,如图2所示。

图2 缺陷面3的网格划分Fig.2 Meshing of defect surface 3
每个网格的节点坐标统一由左上角节点标记,记为eij(xij,yij,zij),因此每个网格的面积可表示为:
(5)
基于管道力磁耦合关系,可以得到每个单元对应的磁化强度Mij。根据磁荷理论[14],磁荷量与垂直于磁体表面的磁化强度呈正相关,缺陷面3上每个单元的磁荷量可表示为:
qij=μ0MijxSij
(6)
式中:qij表示eij单元对应的磁荷量,Wb;Mijx表示缺陷面3上垂直eij单元表面的磁化强度,A/m。
通过式(6)可以得到管道缺陷面3的磁荷分布矩阵q:
(7)
根据磁偶极子理论,每个单元的磁荷在P(xp,yp,zp)点处产生的磁场强度三分量表示为:
(8)
(9)
(10)
(11)
式中:Hijx为缺陷单元在P点产生的磁场强度沿x轴分量,A/m;Hijy为缺陷单元在P点产生的磁场强度沿y轴分量,A/m;Hijz为缺陷单元在P点产生的磁场强度沿z轴分量,A/m;rij为缺陷单元到P点之间的直线距离,m;其他参数同上。
通过将缺陷面3个单元产生的磁场分量进行叠加,即可得到缺陷面3在P点产生的磁场分量:
(12)
(13)
(14)
式中:H(3)x为缺陷面3在P点产生的磁场强度沿x轴分量,A/m;H(3)y为缺陷面3在P点产生的磁场强度沿y轴分量,A/m;H(3)z为缺陷面3在P点产生的磁场强度沿z轴分量,A/m。
应用上述同样的计算方法,可依次得到缺陷其他3个面在P点产生的磁场强度,需要特别注意的是,计算过程中,垂直于磁体表面的磁化强度在不同缺陷面将发生改变。通过对4个缺陷面正负磁荷产生磁场的叠加,最终得到埋地管道缺陷在P点产生的磁场强度三分量:
Hx=H(1)x+H(2)x-H(3)x-H(4)x
(15)
Hy=H(1)y+H(2)y-H(3)y-H(4)y
(16)
Hz=H(1)z+H(2)z-H(3)z-H(4)z
(17)
式中:Hx为缺陷在P点产生的磁场强度沿x轴分量,A/m;Hy为缺陷在P点产生的磁场强度沿y轴分量,A/m;Hz为缺陷在P点产生的磁场强度沿z轴分量,A/m。
P点处磁感应强度三分量表示为:
Bx=μ0Hx
(18)
By=μ0Hy
(19)
Bz=μ0Hz
(20)
式中:Bx为缺陷在P点产生的磁感应强度沿x轴分量,T;By为缺陷在P点产生的磁感应强度沿y轴分量,T;Bz为缺陷在P点产生的磁感应强度沿z轴分量,T。
由于埋地管道磁记忆检测是处于地磁场下的弱磁检测,磁感应强度信号微弱,为了便于判断,目前在实际工程应用中,常采用磁力梯度仪检测,根据磁感应强度梯度模量变化情况判断缺陷位置[15]:
(21)
式中:G为y方向的梯度模量,T/m。
3 应用实例
通过实际案例分析,验证本文提出的计算方法的准确性。某埋地管道材质为X70,其主要化学组成以及力学性能如表1所示。管道直径660 mm,壁厚9.5 mm,埋地深度1.2 m,介质内压3.01 MPa。

表1 X70钢的主要化学组成与力学性能Table 1 Main chemical composition and mechanical properties of X70 steel
管道路线探测工作完成后,使用精度1 nT/m的磁力梯度仪对管道进行磁记忆检测。磁力梯度仪的构成如图3所示,主要包括探测器、控制器和电源3部分,其中探测器两端分别有磁传感器探头。

图3 磁力梯度仪的构成Fig.3 Composition of magnetic gradiometer
管道自漏磁场收集与管道开挖如图4所示。实验管道周围地势平坦,无明显的干扰磁源。手持探测器并保持提离高度0.5 m不变,沿着图4(a)中黑线(管道轴线)行走完成管道自漏磁场信号收集。处理收集的数据时发现1个异常峰值点,其值为1 028 nT/m。经过管道开挖检查,在21.3 m处发现管道上表面存在1个近似凹槽缺陷,长400 mm,宽100 mm,最大深度6 mm。开挖后的管体如图4(b)所示。

图4 管道自漏磁场收集与管道开挖Fig.4 Collection of pipeline self-leakage magnetic field and pipeline excavation
应用文中提出的自漏磁场计算方法,首先借助ANSYS 16.0 Workbench中的静态结构模块Static Structural对含缺陷管道的应力状态进行分析。为了在保证准确性的同时提高计算效率,对缺陷处网格划分进行加密处理,缺陷外的网格划分可适当加粗;同时为了简化计算,忽略土体对管道的作用,只在管道内部施加介质内压3.01 MPa。其中,ANSYS分析得到的结果如图5所示。
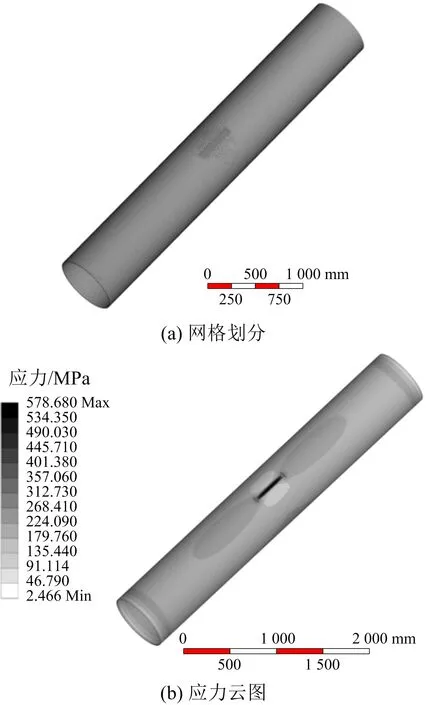
图5 缺陷管道网格划分和应力分析结果Fig.5 Results of meshing and stress analysis for defective pipeline
应力分析完成后,导出应力并根据力磁耦合关系得到每个微小单元的磁化强度。通过计算管道缺陷处每个微小单元磁化强度与其面积的乘积,即可得到缺陷处的磁荷分布矩阵,计算都在MATLAB软件中完成;然后根据公式(8)~(11),并结合缺陷处的磁荷分布矩阵,计算得到缺陷每个单元在检测点产生的磁场强度三分量;接着通过公式(12)~(17)进行叠加计算,得到缺陷处所有磁荷在检测点产生的总磁场强度三分量;最后通过公式(18)~(21)的计算,得到考虑磁荷实际分布时缺陷处的磁感应强度梯度模量,如图6所示。为了对比本文提出的计算方法的准确性,分析了现有方法,计算结果也如图6所示。其中管道磁化参数如下[9]:Ms=1.71×106A/m,a=955 A/m,α=0.8,c=0.099,ε=0.7×108Pa。实验管道所处地磁场三分量:Hgx=12 A/m,Hgy=20 A/m,Hgz=36 A/m。
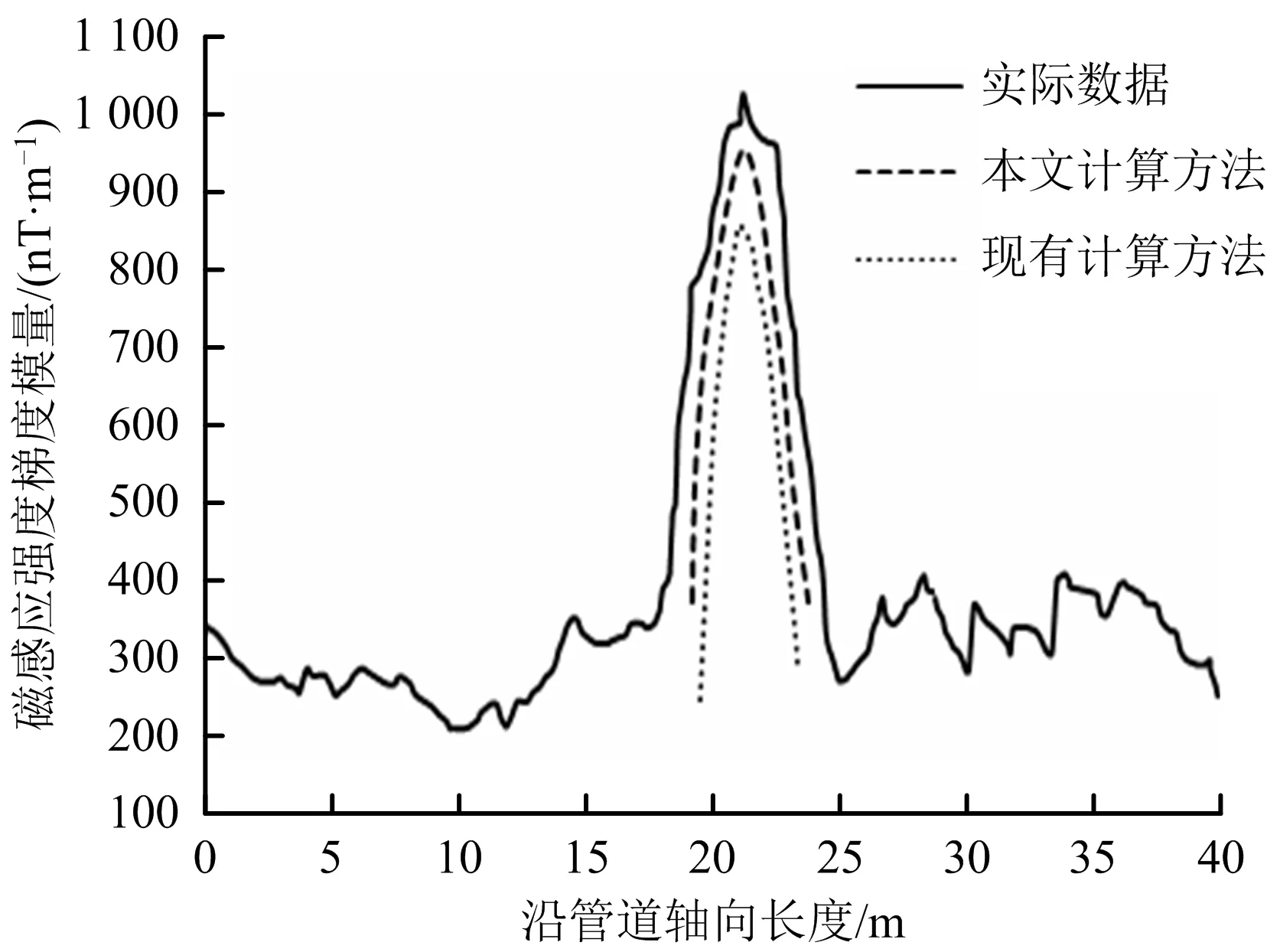
图6 缺陷管道磁感应强度梯度模量实际曲线与理论计算曲线Fig.6 Actual curve and theoretical calculation curves of gradient modulus for magnetic induction intensity of defective pipeline
由图6可知,在埋地管道缺陷处附近,磁感应强度梯度模量的实际测得曲线与理论计算曲线都出现极大值,变化趋势也基本相同。本文方法计算的峰值为957 nT/m,与实际峰值之间绝对误差为71 nT,相对误差为6.9%;现有方法计算的峰值为859 nT/m,与实际峰值之间绝对误差为169 nT,相对误差为16.4%。考虑到现场检测时,外界可能有干扰磁源,或者测量时的人为因素以及仪器本身影响,2种计算方法的误差都在可接受的范围内,都可以为缺陷的检测提供理论指导。不过本文提出的计算方法相对于现有的方法更接近于实际数据,准确度更高,在对缺陷特征进行反演求解时,能更准确的量化缺陷参数,这对管道实际生产运行中的缺陷非开挖识别与剩余寿命评价有着显著影响。
4 结论
1)现有的埋地管道缺陷自漏磁场计算方法未考虑磁荷分布与材料磁化强度的关系,把缺陷处的磁荷假设为均匀分布,使得计算结果与实际检测的误差较大。
2)缺陷处应力的不连续性,使得其磁化强度的分布也具有不连续性;采用ANSYS软件对管道缺陷处进行受力分析,能得到材料缺陷处磁化强度分布;根据磁荷理论,得到缺陷处磁荷的实际分布,提出了考虑磁荷分布的缺陷自漏磁场计算方法;考虑到埋地管道磁记忆检测信号微弱,可以采用磁感应强度梯度模量作为缺陷检测依据。现场应用表明该方法计算结果与实际值之间峰值相对误差为6.9%,相对于现有的方法精确度更高。
3)提出的自漏磁场计算方法有利于提高管道缺陷参数量化的准确性,对缺陷非开挖识别与剩余寿命评价有着重要意义。
