基于模糊聚类方法的S700K转辙机故障诊断

,2

(1.兰州交通大学自动化与电气工程学院，甘肃兰州，730070；2.兰州交通大学光电技术与智能控制教育部重点实验室，甘肃兰州，730070)

转辙机是信号设备室外三大件之一，其缺陷与损害直接影响列车的安全可靠运行。目前，在高速重载铁路中大多采用S700K交流电动转辙机，为了提高其工作的安全性与可靠性，应用智能数据分析处理技术，实现对转辙机工作状态的智能感知和安全预警十分必要。现场对该设备的故障诊断主要依靠工人的工作经验对比功率曲线的变化规律来判断故障，或者设天窗点对现场设备进行定期检修[1-2]。这种故障分析与诊断技术不仅效率低、工作量大，而且容易发生错判、漏判现象而危及行车安全。目前，应用于转辙机智能故障诊断的方法大多针对ZD6直流电动转辙机，对已大量投入使用的交流电动转辙机的故障诊断方案较少，已有的智能故障诊断方案没有充分利用从微机监测系统获取的转辙机动作功率曲线，并且各方法都有其局限性。安春兰等[3]研究了基于小波分解的方法，需要预先设定基函数和分解尺度等参数，小波参数的选择可能影响故障诊断的精度。ATAMURADOV等[4-5]提出了基于专家系统的道岔故障智能诊断方法，知识库完备性的获取和验证困难，当出现新的故障类型时，不能及时添加到故障类型库中。王瑞峰等[6-7]将神经网络及改进后的算法用于转辙机的故障分类，当网络模型扩大时可能出现指数爆炸的现象。肖蒙等[8-9]采用贝叶斯网络进行故障诊断需要提供可靠合理的先验概率，并且当样本数量较小时，故障诊断效果不理想。钟志旺等[10-11]基于支持向量机的故障诊断，原则上只能进行两两分类。EKER等[12-13]分别基于高斯核和最小二乘支持向量机建立了道岔常见失效模式及其控制电路的故障分类器。S700K转辙机动作功率曲线具有非线性、非平稳的特点，故障类型不同，其动作功率曲线不同。模糊聚类分析算法已成功应用于变压器与滚动轴承的故障诊断与分类中[14-16]，它是一种无监督的学习方法，不需要先验知识，完全依靠自身就能够完成多个类簇的划分，转辙机故障样本多、参数难以精确计算，利用模糊聚类分析算法可以克服这些不足。本文作者利用微机监测系统获取的S700K转辙机动作功率曲线，提取在时域表征曲线的标准差、方差、波形因子、脉冲因子以及裕度因子等相关特征指标作为故障特征参数，构建原始特征模式矩阵。采用模糊聚类分析方法，把无类别标记的集合按照某种准则划分成若干子集，将特征模式矩阵中性状最接近的故障模式分为一类，提出一种S700K转辙机智能故障诊断新方法。该方法克服了上述文献中先验概率难以确定以及参数选择影响诊断结果等现象，经过现场实际数据验证，该方法有效提高了故障诊断的精度与效率。

1 转辙机动作功率曲线分析

目前，我国微机监测系统通过采集电流与功率来反映它的工作状态，工作人员利用周期性监测的功率曲线判断转辙机的故障类型。S700K转辙机采用380 V交流异步电机，转辙机的输出功率P与道岔尖轨推拉力F关系[17]如下：

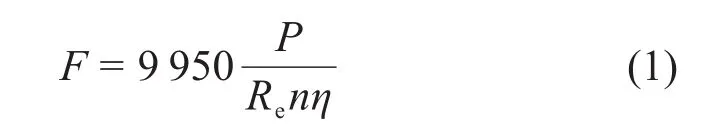
式中：Re为转辙机传动系统等效力臂；n为电动机转速；η为电动机效率。

道岔尖轨推拉力F反映转辙机的运行状态，因此，根据式(1)可以用转辙机的动作功率曲线来反映转辙机的运行状态。

1.1 正常动作功率曲线分析

S700K交流电动转辙机动作过程可分为启动、解锁、转换、锁闭和勾通表示5个过程，其正常动作功率曲线如图1所示。

图1 S700K正常动作功率曲线Fig.1 Normal operation power of S700K

由图1可见：在0.15 s左右时，由于转辙机启动，需要较大的功率，因此，功率曲线骤然上升并且很快达到峰值。随后，由于设备启动完毕，锁舌弹出，转辙机完成内部解锁，进入正常转换阶段曲线急剧下降并趋于稳定。在5.1 s左右时，道岔转换完毕，尖轨密切，功率曲线出现一定幅度的下降，但不会降为0。最后，道岔位置确定，道岔表示电路被切断，功率降为0 kW[18-19]。

1.2 故障功率曲线分析

经过现场调研发现，S700K转辙机在上道使用的过程中经常出现的故障类型如表1所示，每种故障类型所对应的动作功率曲线如图2所示。

2 转辙机故障诊断方法

2.1 故障特征参数的提取

针对S700K交流电动转辙机动作功率曲线非线性、非平稳的特点，提取在时域表征相关特征的指标为标准差、方差、波形因子、脉冲因子以及裕度因子等作为特征参数，构建故障诊断系统的原始特征模式矩阵，提取的特征指标及其计算公式[20]如下：

平均值μ1为

均方根μ2为

标准差μ3为

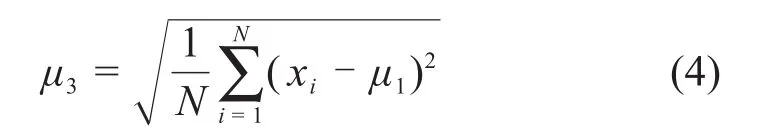
方差μ4为

表1 S700K转辙机常见故障现象及原因Table1 Common failures and causes of S700K switch machine

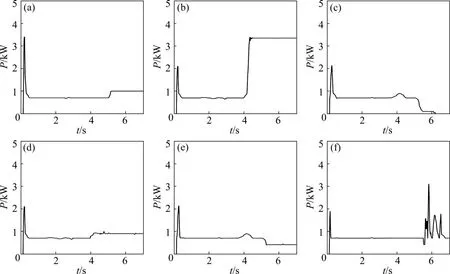
图2 常见故障所对应的功率曲线Fig.2 Power curve corresponding to common fault

最大值μ5为

峭度μ6为

峰值因子μ7为

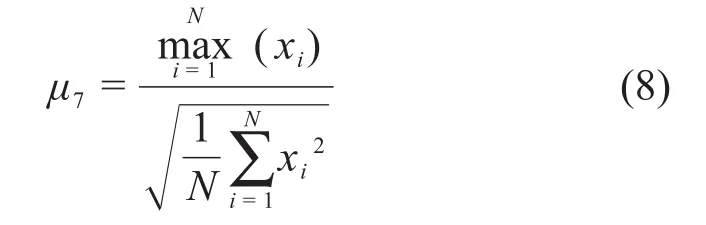
波形因子μ8为

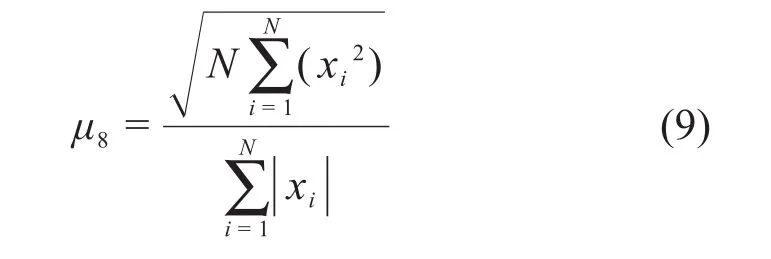
脉冲因子μ9为

裕度因子μ10为

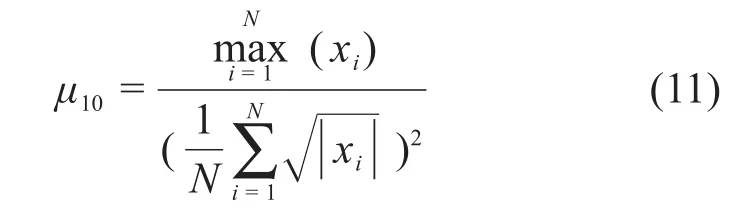
式中：xi为原始信号采样值；N为采样长度。

对微机监测系统数据库获取的转辙机正常运行曲线与典型故障曲线提取以上参数作为表征故障类型的特征值，结果如表2所示。

2.2 模糊聚类分析算法

在模糊聚类算法中，为了进行定量分类，引入描述样本之间相似度的指标rij=R(xi，xj)，其中隶属度R(x，y)表示(x，y)的相关程度。在模糊数学中，若对于任意i=1,2，…，m，j=1,2，…，n，都有rij∈[0,1]，则称R=(rij)m×n为模糊矩阵[21]。

对特征模式矩阵X通过平移标准差变换与平移极差变换进行标准化后，利用距离法得到矩阵R中的每一个元素rij∈[0,1]，即矩阵R是矩阵X上的一个模糊等价关系。由于矩阵R只是1个模糊相似矩阵，不一定具有传递性，为了进行分类，需求出具有传递性的模糊等价矩阵R＊，在R＊中，当λ由1变到0时，分类由粗变细形成动态聚类图。模糊聚类分析算法过程如下：

1)选取S700K电动转辙机不同运行状态下的动作功率数据，包括正常模式和表1中所示的故障模式以及待检曲线，共n种模式，则设论域U={x1,x2,…,xn}，每种模式有m个指标表示其性状，即xi=(xi1,xi2,…,xim)，i=1,2，…，n，于是，得到特征模式矩阵[22]：

为了消除不同量纲的影响，使数据分布在[0,1]之间，需要对原始特征模式矩阵X进行标准化。首先，对原始特征模式矩阵X进行平移-标准差变换：

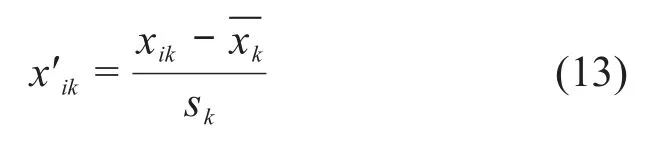
式中：i=1,2， … ，n；k=1,2， … ，m；

经过平移-标准差变换后，每个变量的均值变为0，标准差变为1，且消除了不同量纲对特征模式矩阵造成的影响。但是，经过变换后得到的变量x′ik不一定在区间[0,1]上，因此，需要对变量x′ik进行平移-极差变换使数据分布在[0,1]之间：

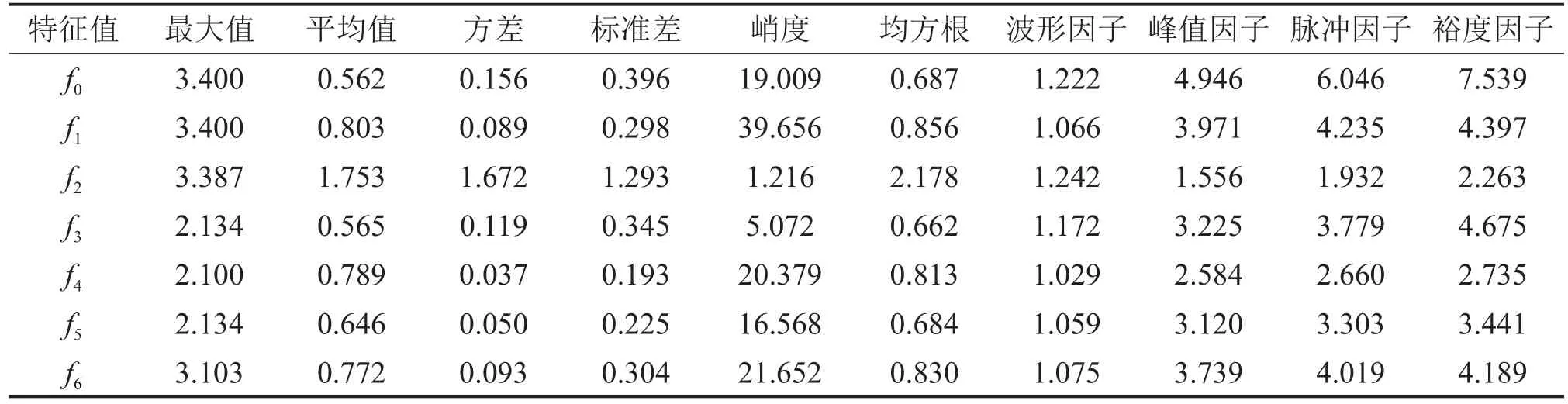
表2 S700K电动转辙机常见故障特征值Table2 Characteristic values of common faults of S700K electric switch machine

2)对标准化后的矩阵X利用描述样本之间相似程度的指标rij=R(xi,xj)建立此矩阵的模糊相似矩阵R。聚类统量rij的确定方法主要有相似系数法与距离法，本文中采用距离法确定rij。在采用距离法时，令

式中：c为使0≤rij≤1的参数；d(xi,xj)为模式xi与xj之间的距离。

常用的距离法有3种，分别为海明距离法、欧式距离法和切比雪夫距离法。

海明距离法：

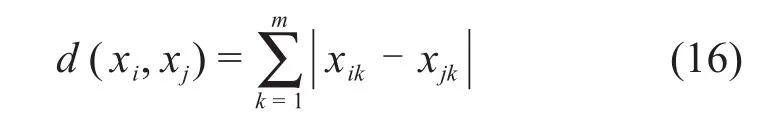
欧式距离法：

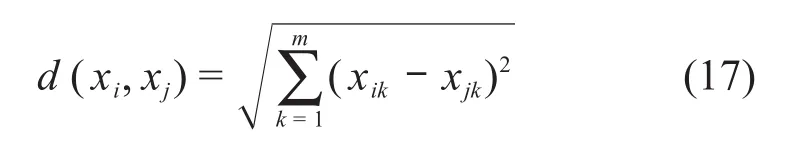
切比雪夫距离法：

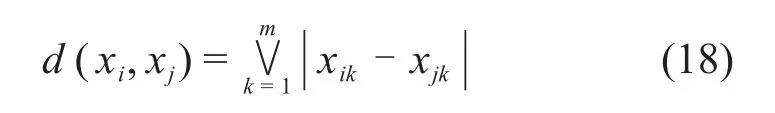
3)模糊相似矩阵R不一定具有传递性，即矩阵R与矩阵X不一定存在等价关系，为了进行分类并形成动态聚类图，需要利用平方法求矩阵R的传递闭包t(R)，将矩阵R改造成模糊等价矩阵R＊。从模糊等价矩阵出发，依次求平方：R→R2→R4→…→R2i→…，当第1次出现Rk∘Rk=Rk时(表明Rk具有传递性)，Rk就是所求的传递闭包t(R)。记Mm×n表示全体m×n模糊矩阵，则R∈Mm×n表示R其中一个m×n阶模糊矩阵。若R∈Mm×n，则存在一个最小的自然数k(k≤n)，使得传递闭包t(R)=Rk，对于一切大于k的自然数l，恒有Rl=Rk，此时t(R)为模糊等价矩阵R*。

4)R*为具有传递性的模糊等价矩阵，且R*=(rij)∈Mm×n，对于任意的λ∈[0,1]，称Rλ=(rij(λ))为模糊等价矩阵R*=(rij)的λ-截矩阵[23]，其中，

则rij(λ)∈{0,1}，即R*的λ-截矩阵为布尔矩阵。在模糊等价矩阵R*中，当λ在[0,1]之间由大到小发生改变时，形成对应的布尔矩阵，从而形成动态聚类图。

3 实例验证及结果分析

选取广铁集团长沙电务段某信号工区某S700K转辙机在运行过程中2个不同时刻的2条故障曲线作为待检样本，验证该算法的可行性。图3所示为某S700K转辙机发生2种不同故障时所对应的动作功率曲线d1和d2。采用式(2)～(11)对图3的功率曲线分别求其特征值，结果如表3所示。经过现场的工人检修后确定该转辙机发生的故障类型与表1中f2和f4所对应的故障类型一致。

根据表3建立特征模式矩阵X，则X=[f0;f1;f2;f3;f4;f5;f6;d1;d2]，根据模糊聚类的思想，需要对矩阵X进行标准化处理，从而消除不同量纲对数据造成的影响，使数据分布在[0,1]之间。利用平移-标准差变换与平移-极差变换对特征模式矩阵X进行标准化处理，得到的矩阵为X＊：

图3 现场某S700K转辙机发生故障时的动作功率曲线Fig.3 Action power curve of S700K switch in event of a fault

表3 待检曲线故障特征值Table3 Fault eigenvalues of pending curve

为了定量进行分类，采用海明距离法作为聚类统计量rij=R(xi,xj)，来描述故障样本之间的相似程度并建立原始特征模式矩阵的模糊相似矩阵R，将R改造成模糊等价矩阵R＊。由前文内容可知矩阵R的模糊等价矩阵R＊=t(R)，则有：

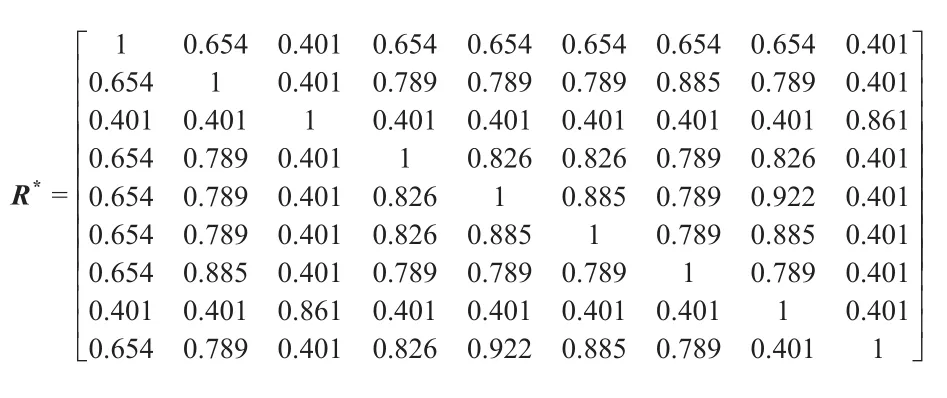
在矩阵R＊中，当λ在[0,1]之间由大到小取值，可得到转辙机故障诊断系统的动态聚类图，如图4所示。由图4可知：当λ=0.861时，当前转辙机运行曲线d1与表1所示故障曲线中的f2性状最相似，当λ=0.992时，当前转辙机运行曲线d2与表1中的f4性状最相似，即2条故障曲线分别对应的故障类型为故障特征集中的f2和f4，这与现场人工检测结果相一致[24]。

为了验证该方法对S700K转辙机故障状态的识别性能，从微机监测系统中获取36组S700K转辙机动作功率曲线数据进行测试，数据量属于小样本情况。在小样本情况下，模糊聚类方法作为故障分类器，比支持向量机(SVM)算法和贝叶斯网络(BN)算法的诊断误报率更低[10]。3种分类器性能比较如表4所示。从表4可见：模糊聚类方法正确率为94.5%；在小样本情况下，模糊聚类方法仍具有较强的预测推广能力。

图4 故障诊断系统动态聚类图Fig.4 Dynamic clustering diagram of fault diagnosis system

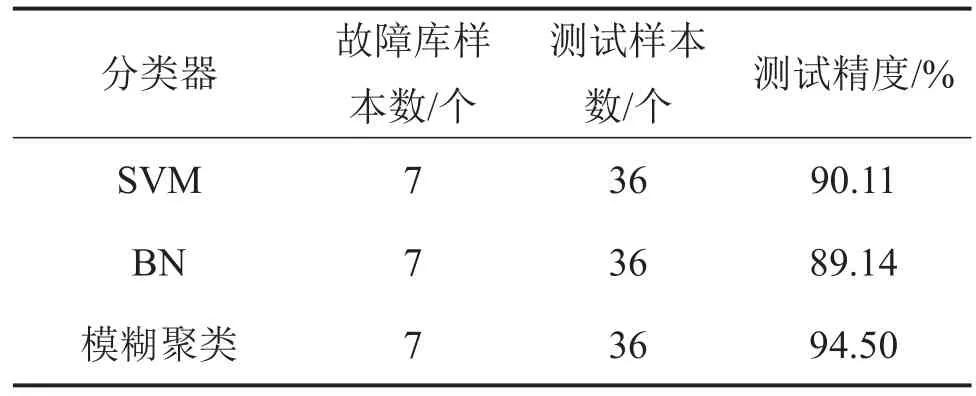
表4 3种分类器诊断性能比较Table4 Comparison of diagnostic performance of three classifiers

4 结论

1)本文针对S700K转辙机典型故障下的动作功率曲线呈非线性、非平稳的变换规律，由表征时域特征量的参数形成特征值，构建原始特征模式矩阵，在此基础上，利用模糊聚类思想对原始特征模式矩阵进行标准化、标定(建立模糊相似矩阵)、聚类，当λ在某一水平取值时，相似度最高的故障被分为同一类，从而达到故障诊断的目的。

2)基于模糊聚类分析算法的故障诊断是一种基于数字信号处理的方法，该方法无需训练，不需要提供大量的先验参数且支持多种故障同时检测，经验证有效提高了故障分类的准确率与效率。