机器人化钻锚车钻臂工作空间分析及轨迹规划

(中国矿业大学(北京)机电与信息工程学院，北京，100083)

煤炭是我国的主体能源，随着浅层煤层的枯竭，矿井正逐年向深部煤层延伸，而深层煤炭开采危险系数高[1-5]，严重威胁井下工人的人身安全，研究表明，煤矿巷道顶板事故是造成人员伤亡最严重的灾害之一[6]。锚杆机是煤矿巷道支护关键设备，主要分为单体锚杆钻机、机载锚杆钻机和锚杆钻车。其中，单体锚杆机及配套设备应用最广泛[7-8]，掘进机机载锚杆钻机应用较多[9]，但这2种装备操作复杂，人员操作危险性大，与掘进机配套串行作业容易引起掘锚失衡问题。近年来，我国引进并研发了较先进的锚杆钻车，如阿特拉斯科普柯Boltec S锚杆台车，虽可以实现高效率完全机械化锚固作业，但并不能与巷道掘进设备配套使用；我国自主研发CMM10-30型十臂锚杆钻车[10]，与掘锚机或连续采煤机等配套组成巷道快速掘进成套装备，但仅适用于顶板较好且允许一定空顶的巷道[11]。因此，缺少一种可以实现掘支锚并行作业、与掘进机配套的且适用于我国深部煤层巷道环境的锚杆钻车。目前，相关研究人员对锚杆钻机的运动学特性进行了大量研究，并取得一定的成果。文国臣等[12]对锚杆钻机变幅机构运动学特性进行研究，通过建立锚杆钻机变幅机构的正向运动学模型，求解并仿真验证了其有效工作空间。岳立新等[13]对锚杆钻机分段运动的控制方法进行研究，通过锚杆钻机正向运动学方程得到各关节运动角度的控制模型，从而确定锚杆钻机在不同巷道高度条件下的工作范围。辛德忠等[14]对全方位钻机钻孔姿态调节装置进行研究，运用D-H分析法建立坐标系并求出钻机结构的运动学方程，并仿真求解出机构有效工作空间。毛君等[15]建立以D-H参数法为基础，在掘进机位姿影响下的7自由度掘锚一体机运动学模型，分析了掘锚一体机的运动学特性和钻头的工作空间。但是，这些研究仅仅分析了锚杆钻机钻头所能到达的工作空间。马齐江等[16]在分析机载锚杆钻机工作空间的基础上，基于ADMAS仿真分析了锚杆钻机钻头的运动学特性，但仅能说明锚杆钻机可以达到预定的动作，并不能保证在运动过程中避开外界的障碍。在此，本文作者结合深部危险煤层综掘巷道智能化、无人化趋势[17-20]，提出一种机器人化钻锚车，实现全自动化自主钻锚作业，且保证在运动中与外界环境不发生干涉。在机器人化钻锚车原理样机基础上，对顶板钻臂和侧帮钻臂进行工作空间分析，确定机器人化钻锚车适用巷道范围；并对钻臂末端路径进行轨迹规划，确定钻臂各关节运动谱及目标运行轨迹曲线，避免钻臂在运动过程中与临时支护支架之间发生干涉。该研究为实现机器人化钻锚车钻臂智能化运动学控制提供参考。

1 机器人化钻锚车结构、功能及运动学建模

1.1 机器人化钻锚车结构功能介绍

针对深部危险煤层巷道需要，为提高掘进作业安全，提高掘进效率，提出了智能化掘支锚联合机组[21]，其中，综掘机实现巷道掘进并具备自主定位、自主纠偏和截割自适应等功能；临时支护架组实现巷道临时支护；钻锚车完成顶板和两帮的支护和锚固。根据巷道支护自动化和智能化需求，提出新一代与掘支锚联合机组配套的机器人化钻锚车，该装备不仅可在巷道掘进的过程中，通过铺锚网-钻孔-装锚固剂-装锚杆连续全自动化钻锚作业，快速同步完成巷道顶板和两帮的支护，而且具备自主定位，钻进协调自适应等功能[22-23]。

为满足巷道顶板和帮板锚固要求，机器人化钻锚车设计为双排四臂式结构，图1所示为机器人化钻锚车原理样机。由图1可见：机器人化钻锚车包括顶板钻臂、侧帮钻臂、车体、锚网存储及输送机构和临时支护机构，其中，顶板钻臂和侧帮钻臂均对称布置于车体前，与车体之间由转动副和平移副联结。顶板钻臂可以在车体上水平移动并旋转一定角度；侧帮钻臂可以在车体上下移动并旋转一定角度。图2所示为钻臂结构图。由图2可见：钻臂主要由钻架、锚杆存储及换装装置、锚固剂喷注装置和钻杆装卸装置组成，单钻臂可以实现钻锚孔、装锚固剂和装锚杆连续全自动化作业。

图1 机器人化钻锚车原理示意图Fig.1 Schematic diagram of roboticized bolting truck

图2 钻臂结构图Fig.2 Diagram of drill arm structure

1.2 钻锚车钻臂运动学建模

顶板钻臂和侧帮钻臂在钻锚车车体上均为对称布置，因此，只需要各选取其中一个钻臂进行分析即可得知另一个钻臂的运动情况，分别选取顶板右钻臂和侧帮右钻臂进行运动学建模。

将钻锚车钻臂等效为功能相同的杆件和关节，依据D-H坐标系构建法则，对该钻锚机械臂坐标系的建立作如下规定：以钻锚车顶板钻臂横向移动轨道所在巷道断面与巷道轴向交点作为初始基坐标系O0x0y0z0，在第i个关节上的坐标系为Oixiyizi，连杆i的坐标原点位于关节i与关节i+1轴线的交点处，连杆i的z轴与关节i+1的轴线重合，连杆i的x轴在关节i轴线和关节i+1轴线的公共法线上，方向从关节i轴线指向关节i+1轴线，连杆i的y轴由右手定则来确定。

1.2.1 顶板钻臂正向运动学建模

根据上述规定，对钻锚车顶板右钻臂每个关节建立坐标系，图3所示为顶板右钻臂D-H坐标系。由顶板钻臂的实际尺寸得到顶板右钻臂的D-H参数，如表1所示，其中：a为连杆长度，α为相邻连杆的扭角，d为相邻连杆的距离，θ为相邻2个连杆的夹角。

图3 顶板右钻臂D-H坐标系Fig.3 D-H coordinate system of the right top drill arm

表1 顶板右钻臂D-H坐标系参数Table1 D-H coordinate system parameters of the right top drill arm

根据建立的D-H坐标系及其参数，通过钻臂相邻关节坐标系之间的矩阵变换得到钻臂末端锚杆钻机相对于基坐标系的正向运动学模型，即锚杆钻机相对于基坐标系的空间位姿。顶板右钻臂坐标变换公式如下：

式中：R(x,θ)表示当前坐标系绕x轴旋转θ角度；R(z,θ)表示当前坐标系绕z轴旋转θ角度；[nx,ny,nz]，[ox,oy,oz]和[ax,ay,az]分别为末端执行器相对于基坐标系的姿态向量；[px,py,pz]为末端执行器相对于基坐标系的位置向量；

经解算变换矩阵为

顶板右钻臂运动学方程为

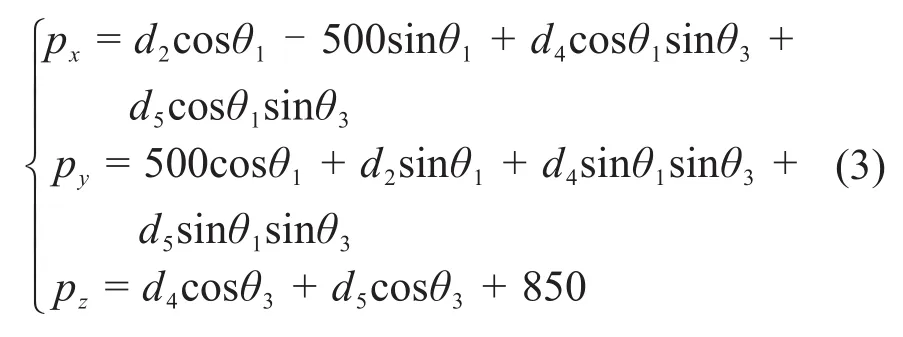
1.2.2 侧帮右钻臂正向运动学建模

依据D-H坐标系构建法则，建立钻锚车侧帮右钻臂的D-H坐标系，如图4所示；由侧帮钻臂的实际尺寸得到顶板右钻臂的D-H参数，如表2所示。

图4 侧帮右钻臂D-H坐标系Fig.4 D-H coordinate system of the right side drill arm

表2 侧帮右钻臂D-H坐标系参数Table2 D-H coordinate system parameters of the right side drill arm

根据建立的D-H坐标系及其参数，通过钻臂相邻关节坐标系之间的矩阵变换，得到侧帮右钻臂末端锚杆钻机相对于基坐标系的运动学模型：

经解算变换矩阵为

式中：

侧帮右钻臂运动学方程为

2 钻锚车钻臂工作空间分析

工作空间是指物体能够达到的目标点的集合，而钻锚车钻臂工作空间是指钻锚机钻头所能覆盖的空间点集。基于蒙特卡洛伪随机数方法提取参数并代入运动学方程，解算钻锚车4个钻臂可到达的工作空间，图5和图6所示分别为钻锚车钻臂工作空间及其xOz平面投影。其中：Ⅰ为侧帮左钻臂工作空间，Ⅱ为顶板左钻臂工作空间，Ⅲ为顶板右钻臂工作空间，Ⅳ为侧帮右钻臂工作空间。

图5 钻锚车钻臂工作空间Fig.5 Working space of drill arm of bolting turck

由图5和图6可见：钻锚车整体适用巷道长×宽最大为6 104 mm×3 844 mm，最小为4 100 mm×2 400 mm，能覆盖长×宽为5 500 mm×3 600 mm的巷道空间所有锚孔，满足巷道支护要求。

图6 钻臂工作空间xOz平面投影Fig.6 Projection of drill arm workspace in xOz plane

3 钻锚车钻臂轨迹规划

通过工作空间分析可以得到在钻臂末端所能达到的空间范围，但在钻臂变位过程中钻臂末端容易出现与临时支护液压支架或底板之间碰撞的现象，因此，还需对机器人化钻锚车钻臂运动轨迹进行规划，以实现在全自动化自主作业中躲避障碍，精确定准锚孔功能。机器人化钻锚车在全自动化钻锚作业中，顶板钻臂对顶板7个锚孔进行锚固，其中右顶板钻机锚固巷道一侧4个锚孔，左右侧帮钻臂分别对左右帮板5个锚孔进行锚固。

3.1 顶板右钻臂轨迹规划

钻锚车顶板钻臂为左右对称布置，选择对顶板右钻臂的运动轨迹进行研究。根据实际工况，设定钻锚车顶板右钻臂完成巷道顶板4个锚孔的钻锚工作的运动时间共120 s，钻臂运动时间不包括钻机钻锚作业时间。图7所示为顶板右钻臂各关节运动步骤，表3所示为顶板右钻臂关节运动谱，其中：A代表移动关节2，B代表转动关节3，C代表移动关节4，与图3中关节对应，箭头指向为该关节的移动方向。

图7 顶板右钻臂各关节运动步骤Fig.7 Movement steps of the right top drill arm joints

根据钻臂运动轨迹的约束条件，三次多项式插值轨迹规划已不能满足钻臂的工作要求，因此运用五项式插值方法规划钻机末端运动轨迹。根据上述对钻臂关节运动的规定，以移动关节2为例作高次多项式插值，首先对关节2在20～40 s的运动轨迹进行计算，通过实际中6个约束条件，对关节2的运动方程进行求解。

设关节2关于时间的运动函数为

对于运动函数的位置约束有：

对于运动函数的速度约束有：

S′(20)=S′(40)=0

对于运动函数加速度的约束有：

S′(40)=0

将所列方程写成矩阵形式为

表3 顶板右钻臂关节运动谱Table3 Articulation spectrum of the right top drill arm

由式(8)可知：6阶矩阵的秩为6，所以，方程存在唯一解，对式(8)求解，得到方程系数a0=-6.26，a1=1.43，a2=-0.10，a3=0.003 5，a4=-0.000 06，a5=-0.000 004。

同理，对关节2、关节3和关节4在各时间段内的运动轨迹方程系数求解。将顶板右钻臂关节2、关节3和关节4在1个周期内各关节随时间的运动轨迹方程代入到运动学方程式中，得到钻机末端的运动轨迹，图8所示为顶板钻臂钻机末端运动轨迹。

临时支护支架顶板厚度200 mm，护帮板厚度75 mm，由图8可见：钻臂末端在x轴最大位移为2 370 mm，距离临时支架护帮板内侧为205 mm；z轴最大位移为3 600 mm,钻臂末端可达到所要顶板目标锚孔位置；变位过程中z轴位移为3 250 mm，低于支架顶梁下边界150 mm，因此，在顶板钻臂运动中可避免与支架顶梁和护帮板之间产生干涉。

3.2 侧帮右钻臂轨迹规划

在式(5)建立的钻锚车侧帮右钻臂坐标系中，杆件1、杆件2、杆件4为虚拟杆件，在钻臂运动时，将其取相应固定值即可。对关节3、关节5和关节6的运动作如下规定。

钻锚车侧帮右钻臂完成巷道侧帮5个锚孔的钻锚工作的运动时间共150 s，钻臂运动时间不包括钻机钻锚作业时间。图9所示为侧帮右钻臂各关节运动步骤，表4所示为侧帮右钻臂关节运动谱，其中：E代表移动关节3，F代表转动关节5，G代表移动关节6，与图4中关节对应，箭头指向为该关节的移动方向。

图8 顶板钻臂钻机末端运动轨迹Fig.8 Trajectory of the end of the top drill arm

图9 侧帮右钻臂各关节运动步骤Fig.9 Movement steps of the right side drill arm joints

表4 侧帮右钻臂关节运动谱Table4 Articulation spectrum of the right side drill arm joint

同样使用高次多项式关节轨迹规划的方法对关节3、关节5和关节6进行关节轨迹规划，并将得到的各关节运动轨迹函数代入式(6)中，得到侧帮钻臂末端的运动轨迹。图10所示为侧帮右钻臂末端运动轨迹。

图10 侧帮右钻臂末端运动轨迹Fig.10 Trajectory of the end of the right side drill arm

由图10可见：钻臂末端在x轴的最大位移为2 750 mm，变位过程中，距离侧帮板250 mm,距临时支护支架护帮板内侧175 mm；z轴的最大位移为3 300 mm，低于巷道支架顶梁100 mm，最小位移高于底板250 mm。因此，侧帮钻臂运动中可避免与临时支护支架及底板产生干涉。

4 结论

1)提出了一种与悬臂式掘进机及临时支护机组配套的机器人化钻锚车，且该装备具备全自动化自主钻锚作业、自主定位和钻进协调自适应等功能。

2)建立了机器人化钻锚车钻臂运动学模型，分析了顶板钻臂和侧帮钻臂工作空间，机器人化钻锚车工作空间能覆盖最大长×宽为6 104 mm×3 844 mm，最小长×宽为4 100 mm×2 400 mm的巷道，能满足长×宽为5 500 mm×3 600 mm的试验巷道的支护要求。

3)对钻锚车钻臂的运动关节进行了轨迹规划，确定钻臂关节运动谱，将基于多项式插值法求出的关节运动轨迹函数代入相应的正向运动学方程中，得到钻机末端的运动轨迹。仿真结果表明：顶板钻臂变位过程中钻机末端距离顶板350 mm，低于巷道临时支护支架顶梁150 mm，侧帮钻臂变位中钻机末端距离侧帮壁250 mm，距支架护帮板内侧175 mm，因此，顶板和帮板钻臂末端的运动轨迹均不会与临时支护支架发生干涉，满足工作要求。