混合骨料级配对充填料浆离析的影响

温震江1，高谦1，陈得信，王永定

(1.北京科技大学土木与资源工程学院，金属矿山高效开采与安全教育部重点实验室，北京，100083；2.金川集团股份有限公司，甘肃金昌，737100)

废石、尾砂等固体废弃物是矿山废弃物的重要组成部分。为了降低矿山充填采矿成本，金川公司利用废石与棒磨砂或戈壁集料进行混合作为充填骨料进行下向分层胶结充填法采矿，不仅提高了充填体强度，满足下向分层充填的要求[1-2]，而且还实现了废弃物资源化利用，由此减小废弃物排放。然而，废石混合充填骨料存在料浆分层离析，不仅导致管道输送过程中的堵管、爆管事故，而且造成胶结充填体分层，从而降低充填体整体稳定性，存在安全生产隐患。虽然影响充填料浆离析因素有很多，但骨料级配是最重要因素之一[3]。针对充填骨料粒径级配，国内外学者已经开展了大量的研究。SANTOS等[4-5]研究表明，采用连续级配骨料配制的自密实混凝土，相比于间断级配骨料混凝土具有更好的抗离析性能；SUN等[6-7]研究发现，通过使各粒级粗细骨料的比率逼近富勒曲线，可以确定最佳级配；张爱勤等[8-9]对泰波理论进行研究，并以此为基础进行骨料级配设计；李洋等[10-11]研究了骨料离析对充填体强度的影响；杨志强等[2,12]研究了骨料离析对料浆流变性的影响。然而，关于骨料级配对充填料浆离析影响的研究较少。在此基础上，本文作者针对金川矿山废石-棒磨砂混合骨料，通过级配设计、建立参数表征骨料级配，结合混合充填料浆离析试验，探究骨料级配对充填料浆离析的影响规律，并对充填骨料优化配比进行分析，以便为混合粗骨料在金川矿山工业化应用中提供理论依据。

1 混合骨料级配设计理论

1.1 粗骨料的界定

在矿山充填领域，粗骨料的界定从混凝土领域借鉴而来，根据美国材料与试验协会(ASTM)对混凝土骨料的划分：粗骨料为粒径大于4.750 mm的骨料，粉料为粒径小于0.074 mm的骨料[13]，细骨料为粒径0.074～4.750 mm的骨料。

1.2 级配设计理论

混合骨料级配应采用连续粒级才能达到较大密实度，因此，基于Wey-Mouth的粒子干涉理论，通过计算次粒级的实积率来设计骨料连续级配[1]。首先，测得堆积密度和表观密度；然后，计算该粒级的理论实积率和实用实积率；最后，根据实用实积率计算各级骨料的分计筛余百分比，由此配置实验所需的粗骨料。

1.3 混合骨料粒径连续分布模型与级配参数

为了研究混合骨料级配对充填料浆离析的影响，采用平均粒径和粒径分散系数2个级配参数表示骨料级配[1,14-15]。根据Wey-Mouth的粒子干涉理论设计骨料级配，在临界状态下，骨料粒径级配是连续的，并且可以达到最大密度，这与Fuller曲线理论相似，因此，基于Fuller公式对设计骨料级配进行函数拟合，建立骨料的粒径连续分布模型，其粒径分布函数F(x)为

式中：F(x)为骨料粒径为x的通过率，%；Dmax为骨料的最大粒径，mm；M和N为拟合系数。

对粒径分布函数F(x)进行求导，得到混合骨料的粒径概率密度函数f(x)。根据混合骨料的粒径分布函数可以求出任意区间内骨料的粒径分布情况[15]。对于某一粒径范围的混合骨料，粒径区间[ɑ,b]的分布概率Pi为

则该体系骨料粒径分散系数ε为

基于式(3)和式(4)，粒径分散系数ε可表示为

根据式(3)～(5)可知，平均粒径和粒径分散系数这2个参数由各粒径骨料综合确定，适合表征骨料体系的级配组成状态。

2 混合骨料物化分析及其配比

2.1 充填骨料物化特性分析

金川矿山充填主要采用废石和棒磨砂的混合骨料，其中，废石主要是在采准和采矿过程中产生，并被破碎至最大粒径为12 mm左右的混合料；棒磨砂是将戈壁鹅卵石经过破碎和棒磨工艺制成的最大粒径为5 mm的骨料。2种充填骨料的物理参数和化学成分分别如表1和表2所示。由表2可以看出：棒磨砂和废石化学成分有明显的差别，废石的化学成分更加复杂，但主要都是由SiO2组成，属于惰性材料，比较稳定，适合作为充填骨料。

2.2 充填骨料级配分析

骨料级配是影响充填效果的重要因素之一。泰波级配理论将粒径不大于d的骨料的质量分数表述成以下形式[16]：

式中：P为粒径x的骨料的通过率，%；n为级配指数。

根据式(6)分别对棒磨砂和废石2种骨料粒径分布进行拟合，结果如图1所示。

由图1可知，废石骨料级配指数n=0.619 9，大于理想状态的Fuller级配指数n=0.5，说明废石中粗颗粒含量偏高，若不掺加一定量的细颗粒改善级配，则在高浓度充填时容易发生沉降离析；而棒磨砂级配指数n=0.307 2，相对于理想状态的Fuller级配指数n=0.5偏小，说明棒磨砂细颗粒偏多，不添加一定量的粗骨料很难形成充填骨架，进而影响充填体强度。

2.3 混合骨料配比确定

单独使用废石和棒磨砂骨料很难满足矿山对充填体强度和料浆流动性的要求，因此，需要将2种骨料按照一定的配比混合以改善充填级配，增大骨料堆积密实度，在保证强度的前提下，降低胶凝材料用量可降低充填成本。根据2种骨料的堆积密实度试验确定骨料配比，试验设计了11种配比试验，分别测定不同配比的混合骨料的密度ρ和松散密度γ，再根据式(7)得出混合骨料的堆积密实度Φ：

2种骨料的堆积密实度模型函数[16-17]为

表1 充填骨料物理参数Table1 Physical parameters of filling aggregate

表2 充填骨料化学成分(质量分数)Table2 Chemical composition of filling aggregate %

图1 废石和棒磨砂粒径负累计分布特征曲线Fig.1 Characteristics curve negative cumulative distribution of waste rock and rod mill sand particles

式中：ρ1为废石粗骨料密度，t/m3；ρ2为棒磨砂细骨料密度，t/m3；混合骨料密度ρ=[w/ρ1+(1-w)/ρ2]-1，0≤w≤1；Φ1为废石粗骨料堆积密实度；Φ2为棒磨砂细骨料堆积密实度；w为废石粗骨料质量分数，%。

按式(8)分别计算不同配比情况下混合骨料的理论堆积密实度，结果如图2所示。

由图2可知，当废石粗骨料质量分数w＜70%时，混合骨料堆积密实度随w增加而增大，此时，废石粗骨料构成“骨架”结构，而细骨料棒磨砂主要起填充空隙的作用；当w=70%时，混合骨料堆积密实度的理论值和实测值均达到最大，这是因为在该配比时满足棒磨砂细骨料恰好能将废石粗骨料形成的“骨架”空隙填满，使得混合骨料最密实；当w＞70%时，混合骨料堆积密实度随w增加而减小，这是由于随着废石粗骨料质量分数的增加，棒磨砂质量分数减少不足以填充废石形成的“骨架”结构，加之粗骨料之间的“边壁效应”进一步阻碍细骨料的填隙，故而使得混合骨料堆积密实度越来越小。

图2 废石-棒磨砂混合骨料堆积密实度曲线Fig.2 Compactness curve of mixed aggregate for waste rock and rod mill sand

因此，为了减少物料种类对离析试验的影响，根据级配设计理论确定采用堆积密实度最大时的废石和棒磨砂配比，即废石与棒磨砂质量比为3:7来进行混合骨料配制、级配参数计算和充填料浆离析试验。

3 混合骨料充填料浆的离析试验

3.1 试验方法

试验主要是借助拌合物稳定性跳桌试验来测试不同级配的混合骨料料浆的离析情况，通过配制不同级配的混合骨料，将其与胶凝材料混合搅拌均匀倒入平均分成上、中、下3层的稳定性检测筒中，然后将筒放在跳桌上振动，振动完成后，分别取出每层的粗骨料进行清洗，待烘干后称质量，然后通过计算得到充填料浆的离析率。

3.2 试验材料

试验材料主要包括废石、棒磨砂和胶凝材料，其中废石和棒磨砂按质量比7:3配制成混合骨料，并且采用标准筛分别配制最大粒径为9.5 mm和12.0 mm的混合粗骨料；胶凝材料选用由北京科技大学开发、甘肃金昌熙金节能建材有限公司生产的“固结粉”新型充填胶凝材料。

3.3 试验方案

3.3.1 混合骨料配制及级配参数计算

为了更好地发挥骨料间的填充作用，以Wey-Mouth的粒子干涉理论为基础，通过控制次级粒径骨料的实积率来配制以12.0 mm为最大粒径的5种级配以及以9.5 mm为最大粒径的3种级配。最大粒径12.0 mm的5种级配，选取其中一种作为标准实积率，编号Z1，并以此为基础进行增减，作为其他几种级配的实积率，Z2的实积率增加0.05，Z3的实积率增加0.08，Z4的实积率减去0.05，Z5的实积率减去0.08；同样地，最大粒径9.5 mm的3种级配，也是选取其中一种作为标准实积率，编为Z6，在此基础上分别增减0.05，得到Z7和Z8。通过筛分实验得到8种级配如表3所示。

根据表3，结合式(1)拟合各个级配的粒径分布曲线，可以得到相应的粒径分布函数F(x)，进而可以得到粒径概率密度函数f(x)，然后根据式(3)～(5)计算各个级配的表征参数平均粒径和粒径分散系数ε。计算结果见表4。

3.3.2 离析率测试

根据跳桌稳定性试验测得上、中、下3层骨料粒径大于4.75 mm的粗骨料的质量，然后根据式(9)计算混合骨料离析率S：

式中：m1，m2和m3分别为上、中、下3层粗骨料的质量，g。

3.3.3 料浆屈服应力测试

屈服应力是表征料浆稳定性的重要指标，与骨料的级配以及料浆离析性有关，如果骨料级配不良，无法实现最大密实度，那么料浆中的粗骨料就容易发生沉降，离析率大，相应的屈服应力反而较小[18]。因此，可以通过建立三者之间的关系控制离析确定合理的骨料级配，反映骨料级配对料浆离析的影响。

当胶砂比为1:4和料浆质量分数为78%时，采用Brookfield R/S plus型浆式流变仪测试料浆屈服应力，根据剪切速率-剪切应力曲线获得料浆屈服应力。料浆离析率及屈服应力试验结果如表5所示。

表3 混合骨料试验级配(质量分数)Table3 Test gradation of mixed aggregate %

表4 混合骨料级配表征参数计算结果Table4 Calculation results of characterization parameters of mixed aggregate gradation

表5 料浆离析率及屈服应力试验结果Table5 Test results of segregation rate and yield stress of slurry

4 试验结果分析

4.1 屈服应力对料浆离析率影响

料浆离析率与屈服应力关系如图3所示，其回归方程为

式中：X为料浆屈服应力，Pa；相关系数R2=0.921 9。

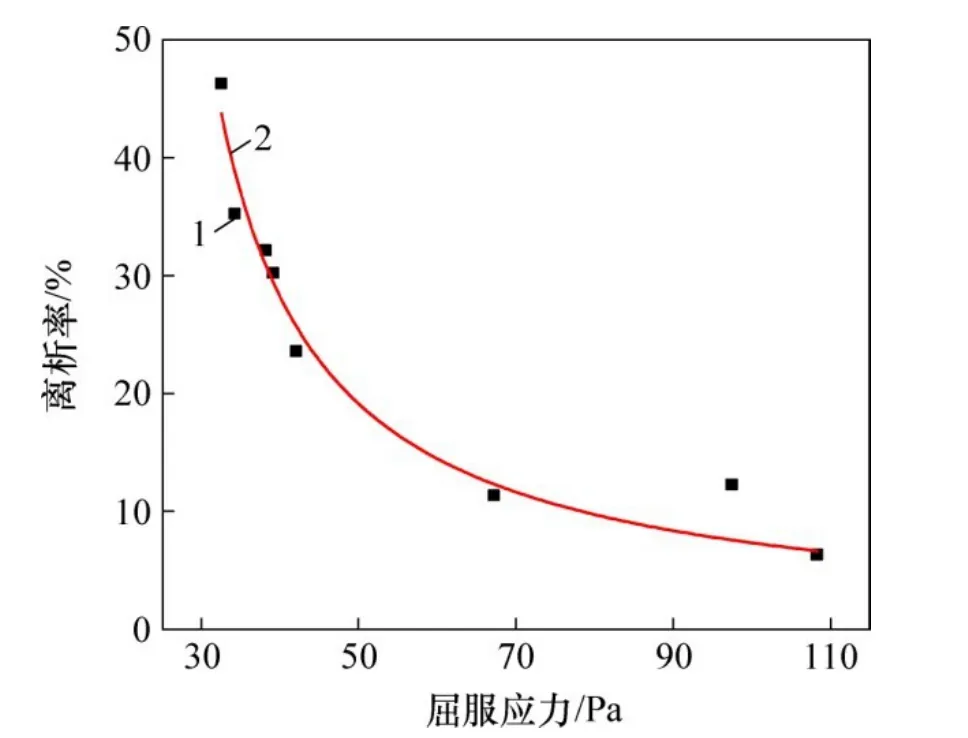
图3 料浆离析率与屈服应力关系Fig.3 Relation between segregation rate and yield stress of slurry

对于高浓度充填料浆而言，不可能完全不发生离析，根据自密实混凝土离析率的规定，离析率不宜大于10%[19-20]，而高浓度充填料浆满足自流输送条件离析率的范围可以通过离析率与充填料浆屈服应力的关系获得。目前，国内外对于膏体和高浓度料浆的划分还没有清晰的界限[21]。张修香等[22-23]研究表明：对于废石-棒磨砂混合骨料而言，当屈服应力介于50～60 Pa时，充填料浆近似为均质体，可以满足金川矿山高浓度自流输送的条件，因此，将其作为条件代入式(10)，得出的离析率范围为16.76%～21.55%。

4.2 混合骨料级配对料浆离析率的影响

基于统计学基本原理建立的平均粒径和粒径分散系数能够很好地表征骨料级配情况，为了探究混合骨料级配对料浆离析的影响，需要建立骨料级配参数与离析率之间的关系。平均粒径与料浆离析率的关系如图4所示，其回归方程如下：

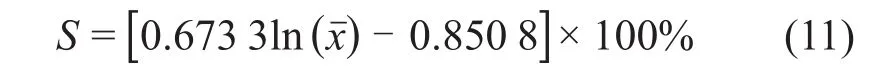
式中：为平均粒径，mm；相关系数R2=0.950 6。

同样，结合表2和表3数据进行回归分析，建立平均粒径、粒径分散系数和离析率三者之间的关系，得出其回归方程为

S=(0.093 5-0.406 2ε+0.287 2)× 100%(12)式中：ε为粒径分散系数；相关系数R²=0.965 6。

根据上述回归方程可知：随着平均粒径增大和粒径分散系数减小，充填料浆离析率增大。为了探究骨料级配对料浆离析的影响，必须对其进行定量分析，找出能够满足高浓度自流输送的条件的骨料平均粒径以及粒径分散系数，因此，根据粒径表征参数和料浆的离析率范围16.76%～21.55%，可以得出满足高浓度自流输送条件的平均粒径为4.99～5.39 mm，粒径分散系数为1.42～1.45。

图4 料浆离析率与平均粒径的关系Fig.4 Relation between segregation rate of slurry and average particle size

5 混合骨料优化设计验证试验

5.1 试验骨料级配及调整

选用金川矿山充填材料即最大粒径为13.2 mm的废石与棒磨砂混合骨料以及固结粉胶凝材料进行验证试验。试验骨料级配Y如表6所示。根据各级粒径通过率进行拟合，并结合式(3)～(5)计算可得出级配Y骨料的平均粒径为5.41 mm，粒径分散系数为1.40，不满足合理范围，因此，需要对级配进行调整。根据Fuller公式并结合上文拟合粒径分布曲线结果可知：N可取0.46和0.49，M近似为100，据此调整后级配T1和T2的粒径如表7所示。由表7可得：级配T1和T2骨料的平均粒径分别为5.04和5.26 mm，粒径分散系数分别为1.44和1.42。

表6 金川矿山混合骨料级配YTable6 Mixed aggregate gradation Y of Jinchuan mine

表7 调整后混合骨料级配(通过率)Table7 Aggregate gradation after adjustment %

5.2 离析率测定及结果

采用Y，T1和T23种级配，制备料浆质量分数分别为76%，78%和80%，胶砂比均为1:4的充填骨料进行离析试验，测定其离析率，结果如表8所示。由表8可以看出：3种级配的骨料的离析率均随着料浆质量分数的增加而减小；在料浆质量分数相同的情况下，级配Y骨料的离析率均比调整后的级配T1和T2的高，尤其是在料浆质量分数为76%的情况下，与级配Y骨料的离析率相比，级配T1和T2的骨料的离析率分别降低了11.71%和10.57%，下降幅度高达37.7%和34.1%，可见：适当的调整骨料级配可以有效控制充填料浆离析。当料浆质量分数为80%时，级配T1和T2的骨料的离析率分别为16.38%和17.04%，与所得满足高浓度自流输送条件的料浆离析率范围16.76%～21.55%比较，仅分别存在1.17%和2.28%相对误差。说明根据满足高浓度自流输送条件料浆离析率所求得骨料级配表征参数范围具有一定的可靠性。

表8 料浆离析率试验结果Table8 Experimental results of segregation of slurry

6 结论

1)以Wey-Mouth的粒子干涉理论为基础设计骨料连续级配，基于Fuller公式对设计的骨料级配进行函数拟合，以此建立骨料的粒径连续分布模型，采用统计学基本原理建立的平均粒径和粒径分散系数能够很好地表征骨料级配情况。

2)单独使用废石和棒磨砂骨料很难满足矿山对充填体强度和料浆流动性的要求，废石和棒磨砂合理质量比为7:3。

3)以屈服应力50～60 Pa为约束条件时，满足金川矿山高浓度自流输送条件的离析率范围为16.76%～21.55%，在此条件下，骨料的平均粒径为4.99～5.39 mm，粒径分散系数为1.42～1.45。

4)料浆质量分数对骨料离析率也有很大影响，在相同级配条件下，骨料离析率随着质量分数的增加而下降，因此，适当提高料浆质量分数可以有效控制离析；另外，适当调整骨料级配可以有效控制充填料浆离析，当料浆质量分数为80%时，级配T1和T2的骨料离析率分别为16.38%和17.04%，与满足高浓度自流输送条件的离析率范围16.76%～21.55%相比较，仅分别存在1.17%和2.28%的相对误差，表明所得骨料级配表征参数范围具有一定的可靠性。