基坑开挖对下卧地铁隧道影响的解析计算方法

,2

(1.中南大学土木工程学院，湖南长沙，410075；2.中南大学重载铁路工程结构教育部重点实验室，湖南长沙，410075)

为最大化利用城市有限的土地资源，在密集的城市地下交通网邻近区域进行新建工程活动不可避免。郑刚等[1]总结了近年国内基坑施工引起盾构隧道变形的代表性工程案例，其中，邻近基坑开挖引起盾构隧道最大隆起量可达33 mm。盾构隧道过大的纵向变形将导致管片开裂、螺栓屈服、接缝张开及渗漏水等病害，严重时还会引起轨道结构不平顺，威胁列车运营安全。CHANG等[2]报道了我国台北某区间盾构隧道在邻近基坑开挖作用下导致隧道结构裂损破坏的案例。可见，开展邻近基坑开挖对既有盾构隧道影响的研究很有必要。当前一些研究者针对该问题分别采用现场实测[3-6]、模型试验[7-9]、数值计算[10-12]及理论解析方法[13-15]等方法开展了相关研究。在这些方法中，现场实测和模型试验往往存在周期长且耗资较大的缺点；数值计算虽然能够较合理地模拟复杂的实际施工过程以及隧道—围岩相互作用，但需要借助于大型商业计算软件，特别是在处理复杂大型模型时，对计算机的性能要求高，计算很耗时。理论解析法具有简便快捷等特点，更适合应用于初步设计和指导工程施工。在既有研究成果中，较典型的作法是将盾构隧道简化为Winkler地基(Pasternak地基)中的Euler-Bernoulli梁(Timoshenko梁)，而作用在盾构隧道上的基坑开挖引起的卸荷作用则可由Mindlin解或其他方法求出，由此建立基坑开挖引起下卧盾构隧道变形的力学模型。该方法思路清晰，力学原理简单，在工程中得到了一定应用，但该方法也存在一些不足，如在模型的建立过程中，认为隧道上覆土层的剪切层参数及地基反力系数为常数，事实上，基坑开挖后，经过扰动后的开挖区域土体抵抗下卧隧道隆起的地基参数会衰减。可见，既有的基于Winkler或Pasternak地基建立的模型难以准确反映下卧隧道实际的受力状态。为此，本文作者在上述模型基础上，进一步考虑基坑开挖后扰动区土体抵抗下卧隧道隆起的地基参数沿隧道纵向不均匀分布，结合工程实例，研究分析上部基坑开挖对既有下卧盾构隧道结构变形的影响，并对基坑分层开挖施工参数进行合理优化。

1 Vlasov地基-Timoshenko梁计算模型

1.1 建模思路

既有研究表明，在研究上部开挖卸载对下卧既有盾构隧道的回弹变形影响时，可将影响范围内的盾构隧道简化为1条细长梁。同时，考虑到盾构隧道通常是由一系列预制管片通过高强螺栓拼接而成，因此，环与环之间的接头部位变形是影响隧道纵向变形的关键因素。SHEN等[16-18]认为盾构隧道纵向变形由弯曲和剪切这2种基本变形模式组成，即盾构隧道发生纵向变形时既受弯又抗剪。传统的Euler-Bernoulli梁理论忽略了梁的剪力对其变形的影响，认为弯矩是导致梁发生挠曲的原因，因此，将盾构隧道简化为Euler-Bernoulli梁实际上低估了隧道的变形。与Euler-Bernoulli梁相比，Timoshenko梁理论同时考虑了弯矩和剪力对梁变形的影响，因此，更符合盾构隧道的实际受力状态。

Winkler地基模型将弹性地基简化为连续分布的、独立的土弹簧，虽然在许多实际应用中能够得到令人满意的结果，但这种模型的主要缺点是不能考虑邻近土弹簧的相互作用，往往会高估地基弹性梁的内力。Pasternak地基模型虽然考虑了邻近土弹簧的相互作用，但土体剪切层参数及地基反力系数往往凭经验选取，缺乏理论依据。此外，这2种地基模型都无法合理地考虑基坑土体开挖后地基参数沿隧道纵向的变化(开挖扰动效应)，而Vlazov地基模型从理论上很好地解决了这个问题。为简化计算，基坑开挖卸荷作用仅考虑弹性变形对下卧隧道的影响，不考虑土体变形的时空效应，可根据Mindlin解计算。

1.2 Timoshenko梁模型

Timoshenko梁的受力变形模式及受力状态如图1所示，其中，p(x)和q(x)分别为地基反力和卸荷荷载，D为盾构隧道直径，T1和T2分别为隧道两侧土体I和II对隧道边界的剪切力(边界效应)。内力与变形之间的关系为：

式中：M和Q分别为弯矩和剪力；E和G分别为梁的弹性模量和剪切模量；I为截面惯性矩；A为截面面积；κ为剪切系数；(EI)eq和(κGA)eq分别为梁的等效弯曲刚度和剪切刚度；w为梁中性轴的挠度；φ为梁截面转角。

图1 Timoshenko梁的受力变形模式及受力状态Fig.1 Force mode and status of Timoshenko beam

根据文献[17]，盾构隧道的(EI)eq和(κGA)eq可分别采用如下2式计算：

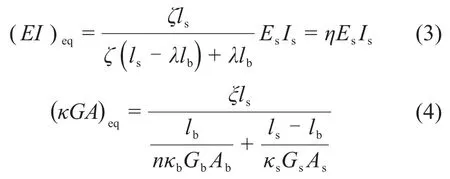
式中：ζ为环向接头的旋转刚度系数；ls为衬砌管片环宽；lb为纵向连接螺栓长度；η为弯曲刚度缩减系数，一般可取为1/5～1/7[19]；EsIs为混凝土衬砌管环的弯曲刚度；ξ为考虑管环之间接触作用的修正系数；κb和κs分别为螺栓和管环的Timoshenko剪切系数，取0.9和0.5[15]，Gb和Gs分别为螺栓和管环的剪切模量；Ab和As分别为螺栓和管环的截面面积；n为纵向连接螺栓数量。

1.3 Vlazov地基模型

Vlazov地基模型如图2所示。地基反力p(x)与挠度w(x)的关系为

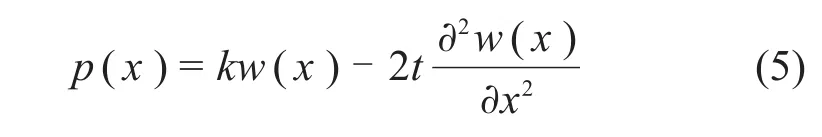
式中：k为地基反力系数；t为土层剪切参数。k和t可采用如下公式计算[20]：

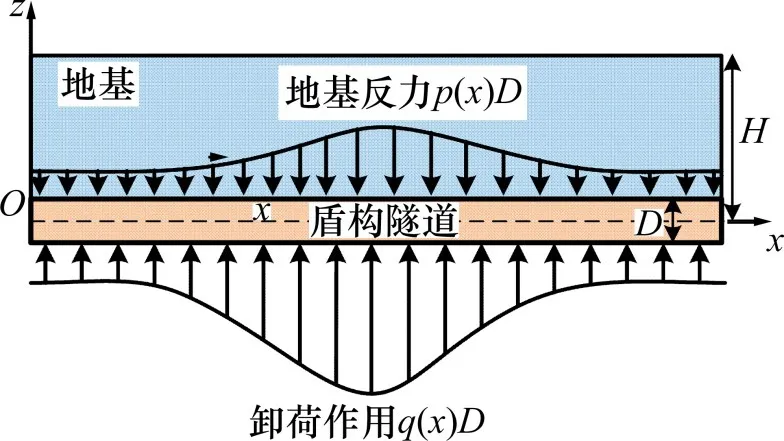
图2 Vlazov地基模型Fig.2 Vlazov foundation model

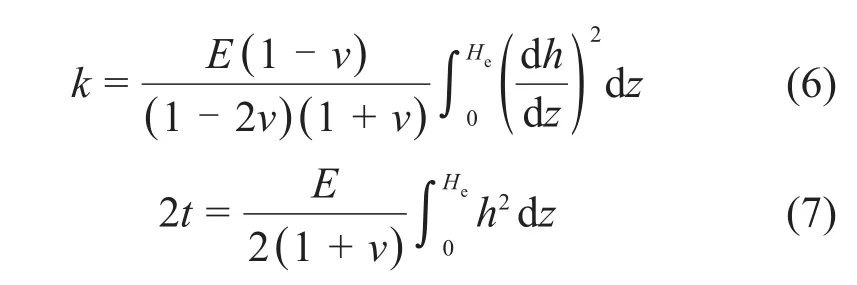
式中：E和v分别为土的弹性模量和泊松比；He为地基弹性层厚度，文献[15,21]建议将He取盾构隧道直径的2.5倍；h=h(z)，为描述z方向位移变化的函数，一般可取为线性或指数变化的函数，本文采用线性函数的形式。基坑开挖后，当隧道上覆土层厚度Hf小于He时，式(6)和(7)中应取隧道实际的覆土厚度Hf。

1.4 基坑开挖卸荷作用

开挖卸荷作用q(x)可采用Mindlin解计算，计算模型示意图见图3。

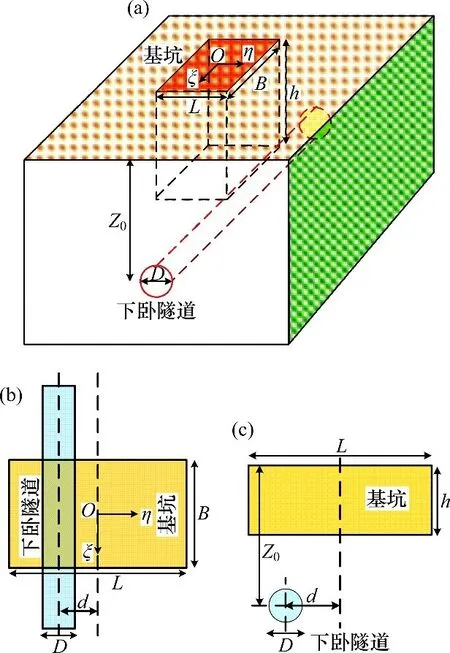
图3 卸荷作用q(x)计算模型Fig.3 Calculation model of unloading stress q(x)

式中：

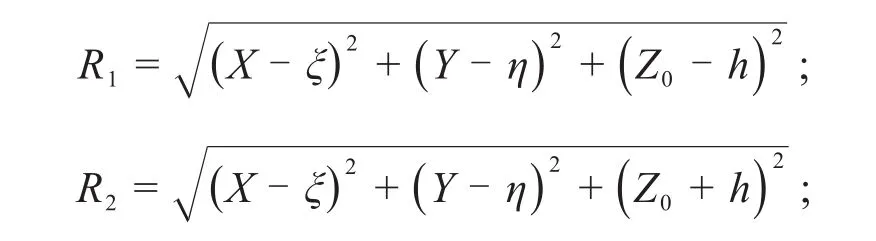
v为土的泊松比；L，B和h分别为基坑的长度、宽度和深度；Z0为下卧隧道中心的埋深；X和Y分别为ξ-η坐标系下的横坐标和纵坐标；和Hi分别为各土层的重度和厚度。若基坑和隧道非正交，则作用于隧道上的卸荷作用可根据文献[14]中的方法进行简单坐标变换后进行计算。

2 基坑开挖对下卧盾构隧道的影响及其验证

2.1 模型求解

由上部基坑开挖引起的下卧盾构隧道的受力状态如图1(b)和(c)所示。以往的研究[13-16]均未考虑该剪切力T1和T2的作用，为此，本文考虑T1和T2的影响，注意到其对称性，可认为T1=T2[21]。

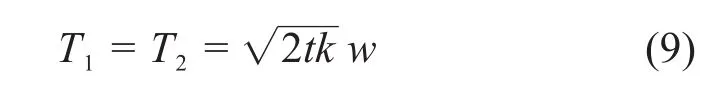
由静力平衡关系，有

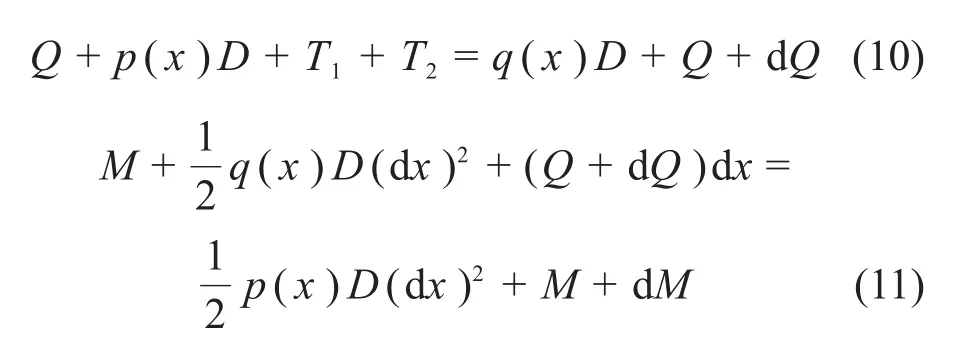
忽略二次高阶项(dx)2，将式(1)，(2)，(5)和(9)代入式(10)和(11)得：

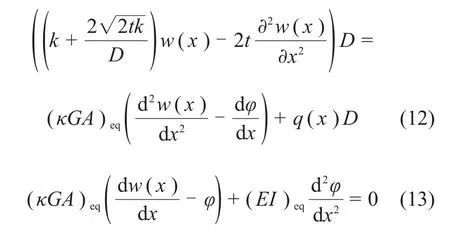
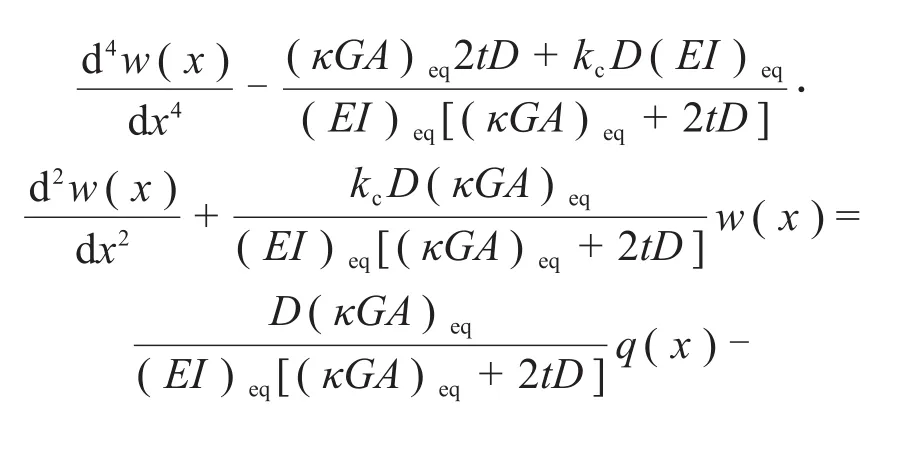
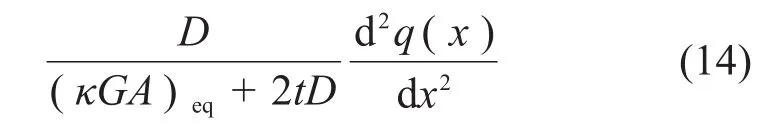
直接求出式(14)的解析解较困难，可采用有限差分法求出上式的近似解。图4所示为基坑分台阶开挖的典型工程案例的计算模型。将隧道分为n+4个单元，单元长度为l，共n+5个节点。其中-2～n1节段、n1～n2节段、n2～n3节段、n3～n4节段和n4～(n+2)节段的地基反力系数分别为k1～k5，剪切系数分别为t1～t5，可分别根据式(6)和式(7)计算。求解出的隧道挠度w为

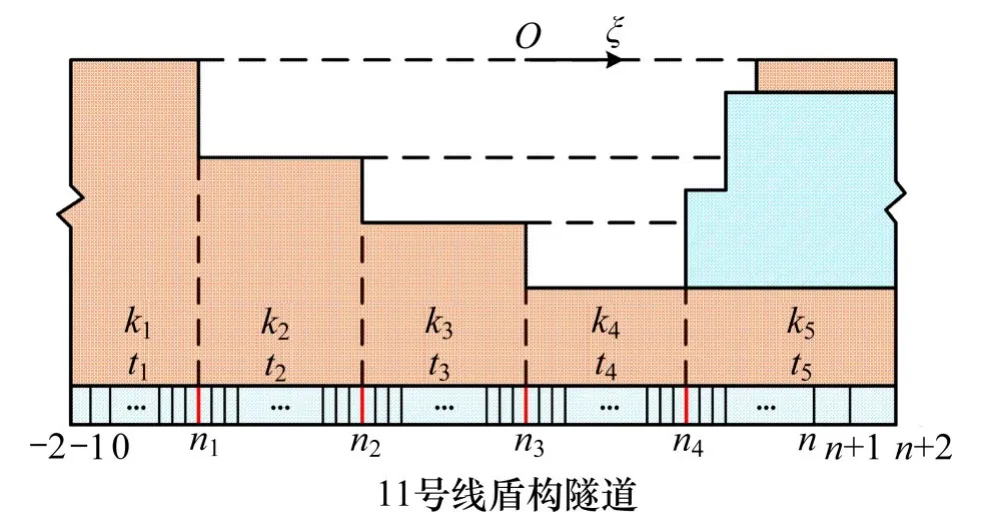
图4 有限差分法计算模型Fig.4 Model of finite difference method

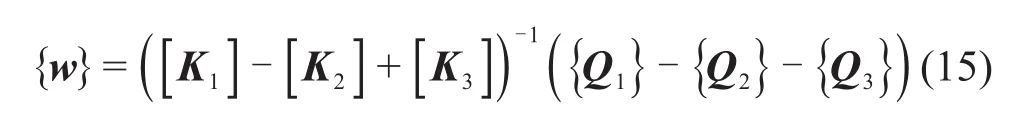
式中：{w}=[w0,w1,w2,…,wn]T；

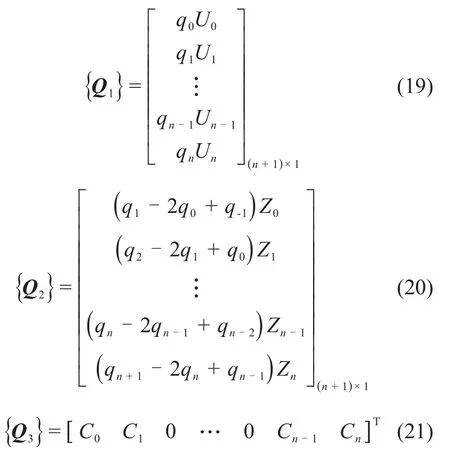
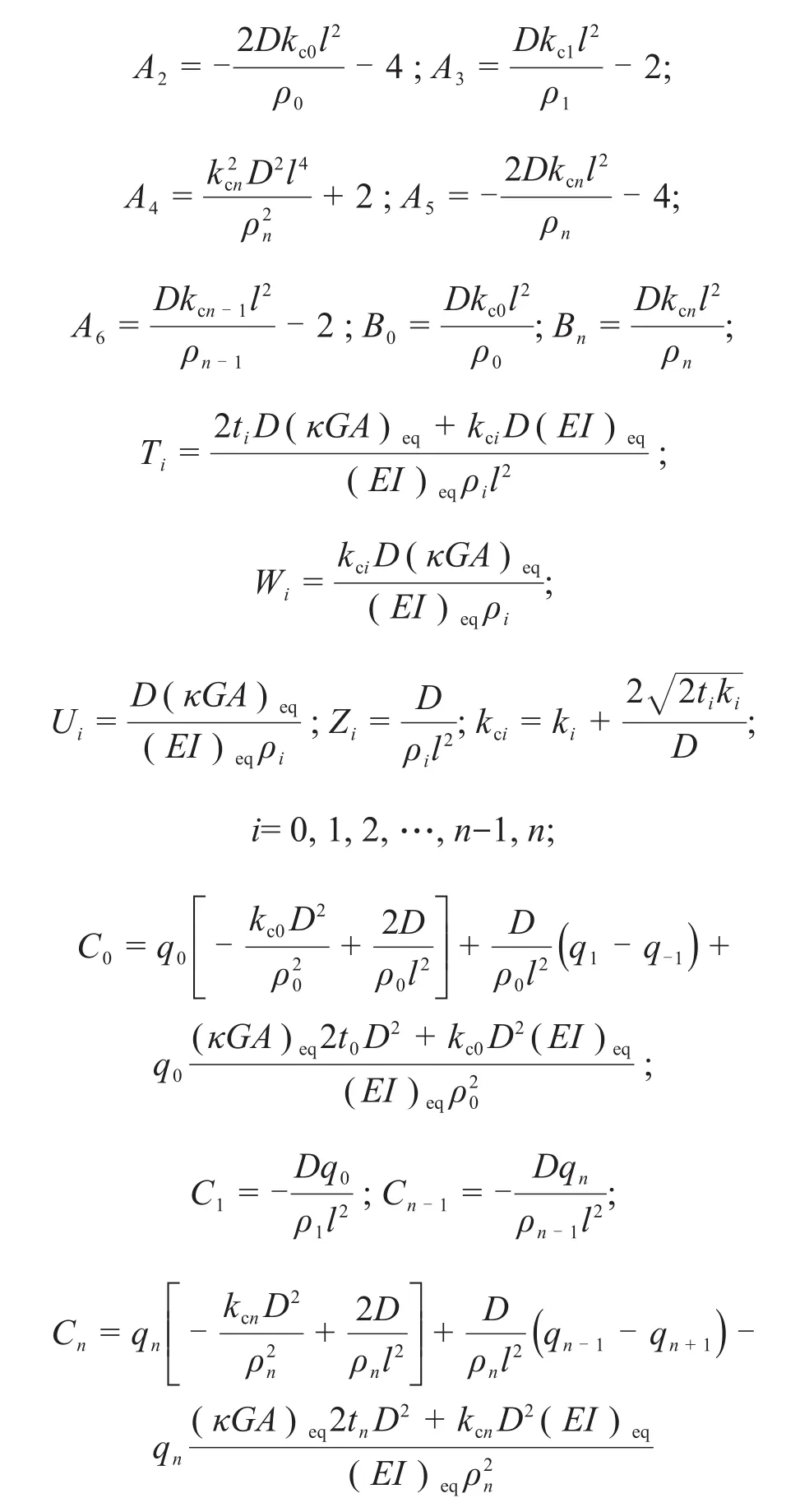
且有

需注意的是：若等效剪切刚度(κGA)eq足够大，则隧道模型退化为Euler-Bernoulli梁；若土层剪切参数t为0，则地基模型退化为Winkler地基。

2.2 模型验证与对比分析

为验证本文模型，对于文献[22]中的工程案例，基坑与下卧盾构隧道的相对位置关系如图5所示。基坑的长度、宽度和深度分别为50.00，10.00和11.00 m，其底板与下卧隧道的净距仅为5.50 m。隧道的外径及壁厚分别为11.00 m和0.55 m，其等效弯曲刚度和剪切刚度分别为3.99×1011N·m2和3.38×109N。地层由上而下分别为18.00 m厚的黏土层，30.00 m厚的粉质黏土层及16.00 m厚的砂质粉土层。相关力学参数见表1。

图5 基坑与隧道相对位置关系Fig.5 Relative position between tunnel and foundation pit

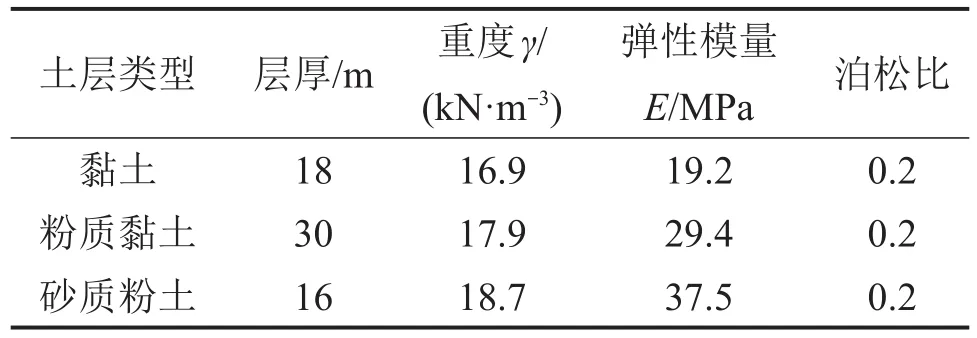
表1 土层相关力学参数Table1 Related mechanical parameters of soil layers

为反映本文方法与不考虑基坑开挖扰动效应方法的差别，将盾构隧道简化为Timoshenko梁和Euler-Bernoulli梁，地基模型分别采用Winkler模型和Pasternak模型。四者之间的组合分别为：Timoshenko-Winkler模型(T-W模型)，Timoshenko-Pasternak模型(T-P模型)，Euler-Bernoulli-Winkler模型(EB-W模型)和Euler-Bernoulli-Pasternak模型(EB-P模型)。几种方法计算的基坑开挖引起的下卧隧道的变形如图6所示。由图6可知：本文模型计算结果与文献[22]采用数值计算所得结果相吻合，从而验证了本文方法对预测邻近基坑开挖引起的隧道变形的适用性与准确性。TW和EB-W模型都会产生不合理的计算结果，T-P和EB-P模型由于无法考虑基坑开挖扰动效应，其计算结果均偏小，存在一定误差。此外，将盾构隧道简化为Euler-Bernoulli梁的模型所得计算结果均小于将其简化为Timoshenko梁的计算结果。可见：本文考虑弯矩和剪力对隧道纵向变形的影响以及基坑开挖扰动效应，将盾构隧道简化为Vlazov地基中的Timoshenko梁，提出的模型具有一定的适用性和准确性。

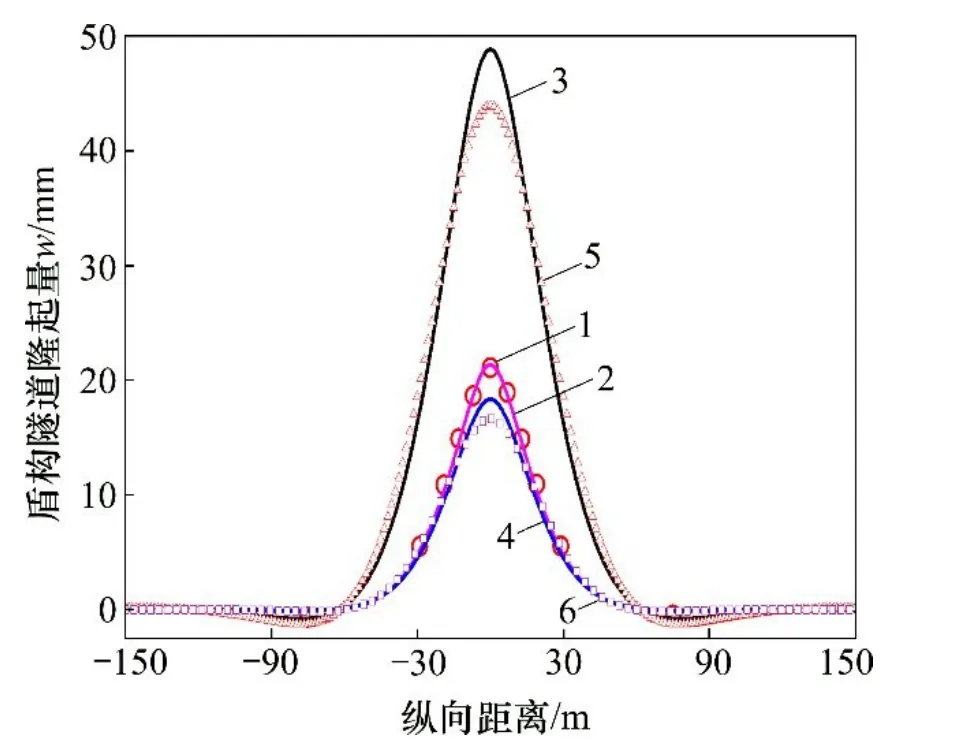
图6 基坑开挖完后几种方法隆起量计算结果对比曲线Fig.6 Comparison of results computed by several methods after excavation of underlying metro tunnel

3 工程应用

3.1 工程概况

深圳市桂庙路快速化改造工程西起规划振海路，止于后海滨路，道路全长约4.90 km。桂庙路改造工程需要在既有地铁11号线上采用明挖法修建双洞矩形公路隧道，共线长度约3.00 km，典型相对位置关系见图7。基坑开挖深度约14.00 m，宽度38.20 m，采用直径为1.00 m、间隔为0.11 m、长度为15.50～23.00 m的钻孔灌注桩，桩间内外设直径为0.6 m高压旋喷桩止水的围护结构型式。共线段地铁11号线盾构隧道左、右两线均位于基坑下方，隧道内径为6.00 m，壁厚为0.35 m，与基坑底板净距为8.50 m，左、右两线中心距离基坑中心线分别为4.74 m和17.04 m。

图7 基坑与下卧盾构隧道相关位置关系Fig.7 Relative position between foundation pit and underlying shield tunnel

工程场地地质条件复杂，地层自上而下依次为人工填土、粗砂、黏土、淤泥质黏土、砾砂和砾质黏性土，如图7所示，相关力学参数见表2。计算中，土体平均泊松比取0.25。

表2 各层土相关力学参数Table2 Related mechanical parameters of soil layers

为保证施工进度和线路纵向土体稳定性，设计采用全幅、分层开挖。开挖分3个台阶进行，台阶高度分别为6，4和4 m，台阶步长均为6 m。简化后的基坑纵向开挖示意图如图8所示。

3.2 计算结果与实测结果对比验证

深圳市地铁11号线盾构隧道相关参数如表3所示。盾构隧道的等效弯曲刚度(EI)eq和等效剪切刚度(κGA)eq分别为 1.74×1011N·m2和 3.07×109N。根据桂庙路改造工程实际情况，采用本文所述的理论解析法对基坑开挖所致下卧地铁11号线隆起变形进行计算，并与现场监测数据和T-P模型的计算结果进行对比验证。

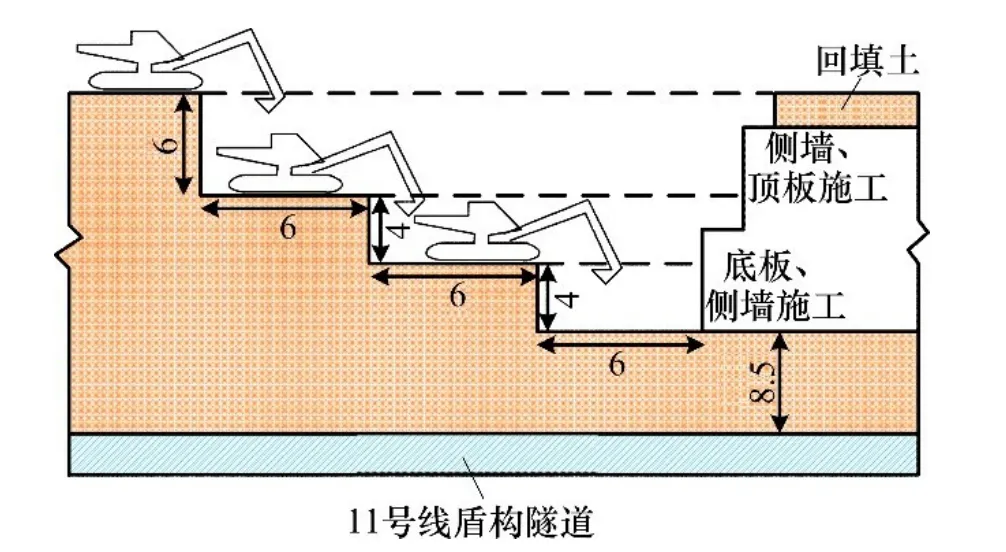
图8 基坑纵向开挖示意图Fig.8 Diagram of longitudinal excavation of foundation pit

表3 地铁11号线隧道结构参数Table3 Parameters of metro line 11

图9 基坑开挖完后隧道隆起量计算及实测结果对比曲线Fig.9 Comparison between calculated and measured results of tunnel deflection after excavation

图9所示为基坑全部开挖完后，地铁11号线左、右两线的隆起变形实测值与理论计算结果。由图9可知：因为基坑开挖引起的隧道变形较小，这2种方法的计算结果均与现场实测结果较吻合。本文计算结果和偏移中心的幅度比T-P模型的稍大，这是由于T-P模型忽略了基坑开挖扰动对上覆土层地基参数的影响，即地基参数沿隧道纵向保持不变，实际上低估了下卧隧道的变形。此外，在纵向距离0～60.00 m范围内，本文方法的计算结果与T-P模型所得结果相比更接近于现场实测结果。

3.3 施工优化

现有的基坑开挖施工方案对下卧地铁11号线的影响有限，实测最大隆起量仅为7.40 mm。在满足盾构隧道隆起变形值不超过既有控制标准的前提下，兼顾施工进度的要求，需要对现有的施工方案进行优化，具体包括三台阶法开挖每层台阶高度的优化及台阶步长的优化。

“上海市地铁沿线建筑施工保护地铁技术管理暂行规定”[23]和GJJ/T 202—2013“城市轨道交通结构安全保护技术规范”[24]均对盾构隧道竖向变形提出了具体要求，竖向变形控制在20.00 mm以内。基于此，本文将盾构隧道隆起变形20.00 mm作为控制值，16.00 mm作为报警值，12.00 mm作为预警值。结合本文提出的理论解析法，对相关施工参数进行优化。

3.3.1 开挖台阶高度的优化

如图8所示，现场施工3个台阶高度分别为6，4和4 m，步长均为6 m。在这部分研究中，台阶步长仍为6 m，3个台阶高度分别取为：6，4和4 m(工况1)；4，6和4 m(工况2)；4，4和6 m(工况3)。计算结果如表4所示。

表4 不同工况的计算结果Table4 Results of different conditions

由表4可知：相较于原施工方案(工况1)，工况2和3都有利于减少下卧盾构隧道的隆起量，其中工况3效果最好。究其原因，这3种工况下的基坑土方开挖量分别为6 876，6 417.6和5 959.2 m3，较少的土开挖量有助于控制隧道的隆起变形；另一方面，当第1和第2个台阶开挖高度均为4 m时，盾构隧道上覆土层厚度较大，相应的地基参数要比工况1和2的高，有利于抵抗隧道隆起。因此，这3种施工方案的控制效果中，工况1最差，工况2一般，工况3最好。在实际工程施工中，建议将3个台阶开挖高度调整为4，4和6 m。

3.3.2 开挖台阶步长的优化

由上述分析可知，当3个台阶的高度分别为4，4和6 m时，对下卧盾构隧道的隆起变形控制是有利的，所以，这部分研究中采用工况3的台阶高度施工方案，以表4中变形指标值为控制目标，对施工台阶步长进行优化，每个台阶步长取为6～42 m，计算结果如图10所示。

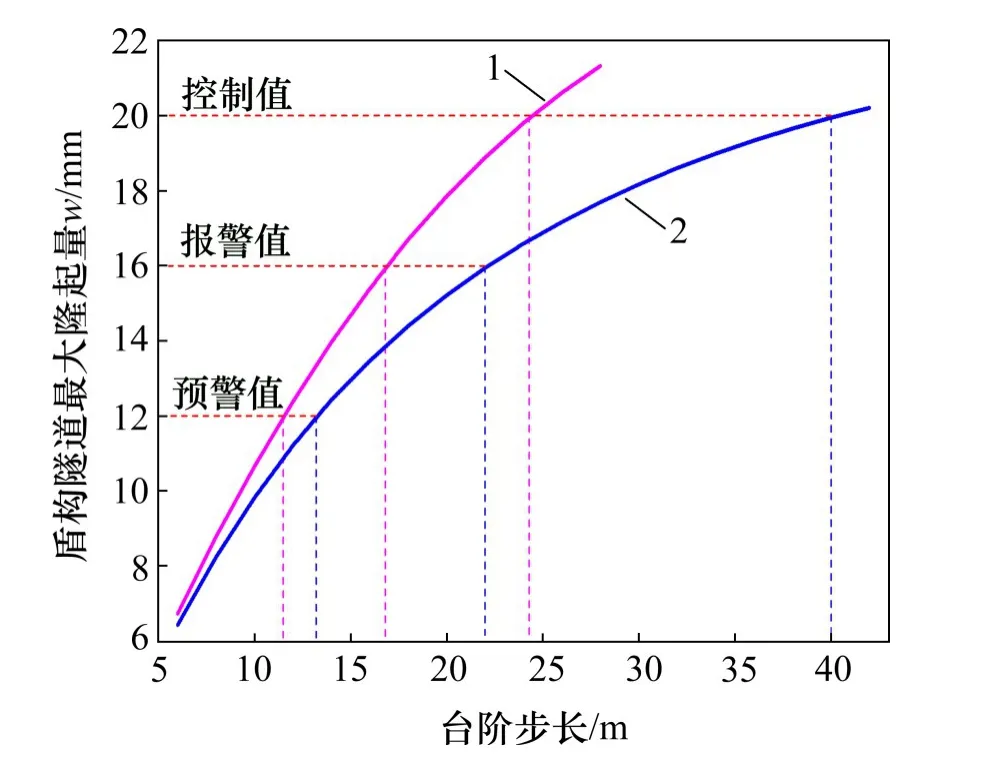
图10 隧道最大隆起量与台阶步长的关系Fig.10 Relationship between the maximum tunnel deformation and step length

由图10可知：本文方法预测的盾构隧道最大隆起量达到预警值、报警值和控制值所对应的台阶步长分别为11.5，16.8和24.3 m；而不考虑开挖扰动效应时(T-P模型)预测的隧道隆起量达到3个指标所对应的台阶步长分别为13.2，22.0和40.0 m。当台阶步长分别为13.2 m和40.0 m时，两者计算的挠度曲线如图11所示。由图11可知：当基坑开挖尺寸较大时，两者的计算结果偏差比较明显，并且不考虑开挖扰动效应时明显低估隧道的变形，给下卧盾构隧道带来安全隐患。当隧道隆起量达到预警值时，应采取必要的控制措施并密切监控隆起的进一步发展；当达到报警值时，要立即采取有效措施和手段(如覆土堆载等)对隆起进行控制；当达到控制值时，将导致结构破坏等严重工程事故。因此，为降低基坑开挖对下卧盾构隧道的影响，在不增加额外隧道隆起变形控制措施的条件下，对于本工程案例，应控制基坑台阶施工步长小于11.5 m。如对于标段K3+980～K3+786(共194 m)，若开挖步长为11 m，则可分为17段，按照每段施工时间5 d计算，需要85 d完成，若保持原施工步长6 m的方案，则需要160 d完成，可缩短75 d的施工工期，大幅度加快了施工进度。

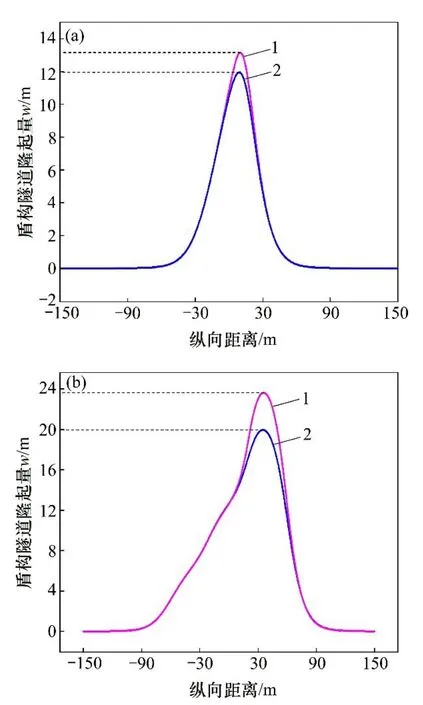
图11 不同开挖步长计算的隆起量曲线Fig.11 Deflection curves calculated by different excavation steps

4 结论

1)考虑基坑开挖扰动对下卧盾构隧道上覆土层地基参数的影响，认为基坑开挖扰动会造成上覆土体的剪切参数和反力系数沿隧道纵向不均匀分布。将盾构隧道简化为Vlazov地基中的Timoshenko梁，作用在下卧盾构隧道上的基坑开挖卸荷作用采用Mindlin解计算，建立了基坑开挖对既有下卧盾构隧道隆起变形量的理论计算方法，并与既有研究结果和现场实测结果进行了对比验证，结果表明两者较吻合。

2)结合盾构隧道隆起变形控制标准，对依托工程的基坑分层开挖高度、台阶步长施工参数进行了优化计算，将3个台阶高度由原来的6，4和4分别调整为4，4和6 m，台阶步长可由原设计的6 m调整为11 m，不仅可以满足下卧盾构隧道的安全要求，而且可以大幅度加快施工进度，缩短工期。