基于特征参数的频率域海洋可控源电磁数据反演影响因素分析
2019-10-16
(中国海洋大学海洋地球科学学院,山东青岛,266100)
可控源电磁法(controlled-source electromagnetic methods,CSEM)已成功应用于海底油气、天然气水合物及矿产资源勘探中[1-2]。频率域海洋CSEM通常的工作方式是在海底上方拖曳电偶极子源,发射频率为0.1~10 Hz的电磁信号,并在海底布设接收站采集经过海底地层传播的电磁信号[3]。当前频率域海洋CSEM一维反演[4-8]和二维反演[3,9-13]发展较为成熟,三维反演算法在不断发展中[14-16]。在海洋CSEM反演研究方面,前人的工作主要集中在反演算法的选取[9,17-24]、反演网格及初始模型的选择[3,15]和正则化参数的选取[9,14]等方面,而对电磁场分量、发射频率和观测模式的选取研究较少。常规的海洋CSEM反演以轴向观测模式下的单频轴向电场分量反演为主[25],KEY等[4,8]通过理论模型的反演测试发现,使用多频率数据、多分量电磁场数据或混合观测模式参与反演均能明显改善反演结果,但未给出反演结果改善的理论依据。为探究一维时间域海洋CSEM对海底天然气水合物的分辨能力,EDWARDS[26]提出特征参数分析方法来研究电磁场数据的分辨率,即对雅可比矩阵进行奇异值分解(SVD),利用特征参数来定量分析反演参数耦合性,以此为依据确定地层电阻率或层厚在反演中能否重构。SCHOLL等[27]使用特征参数分析方法研究了时间域海洋CSEM法对海底高阻层的分辨能力。HÖLZ等[28]使用特征参数分析方法分析时间域海洋CSEM中的旋转不变量参数,结果表明使用旋转不变量数据进行共中心点反演可以较好地恢复海底电性结构。SWIDINSKY等[29]进一步研究了时间域海洋CSEM法中发射源导航参数和海底电阻率参数的同步反演问题,发现在反演过程中,发射源导航参数和地下电阻率是解耦的,反演可以同时重构这2类不同参数。LI等[30]则对频率域海洋CSEM法中的发射源导航参数和电阻率进行了同步反演。本文在实现了频率域海洋CSEM一维反演的基础上,考察反演中电磁场分量、发射频率和观测模式对反演结果的影响,使用特征参数分析方法深入分析造成这些影响的原因,并将特征参数分析方法应用于实际数据的反演。
1 基本理论
1.1 海洋CSEM一维反演算法
一维层状电阻率各向同性介质中水平电偶极子和垂直电偶极子激励下源的位函数及电磁场的表达式可由矢量位函数推导得到[7],在正演过程中采用ANDERSON[31]给出的801点汉克尔变换滤波系数,可保证在较高频率时计算结果的准确性。
高斯-牛顿法同时利用了目标函数的一阶导数和二阶导数信息,具有较好的收敛性[32],已广泛应用于CSEM反演中[8-9,18,23,33]。本文的海洋CSEM一维反演使用的便是高斯-牛顿法。基于正则化约束建立反演目标函数如下:
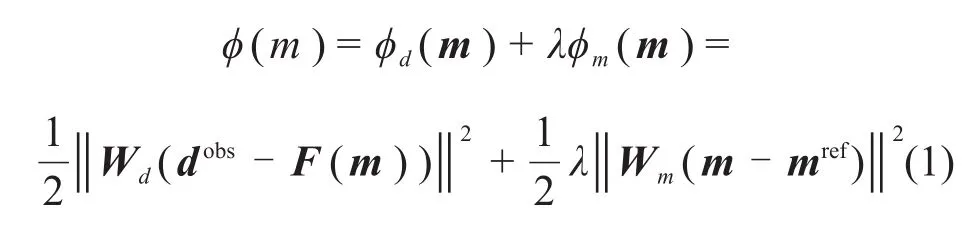
式中:ϕd(m)为数据拟合泛函;ϕm(m)为模型稳定泛函;m为模型参数(电阻率的对数lgρ);mref为包含先验信息的参考模型;λ为正则化参数;dobs为观测数据;F(m)为正演响应函数;Wm为模型加权矩阵;数据加权矩阵Wd为与数据标准差有关的对角矩阵,其表达式为[17]:
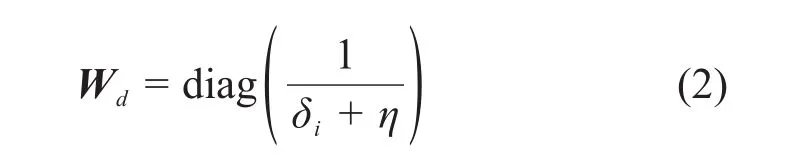
δi(i=1,…,Nd)为第i个数据的标准差,Nd为观测数据个数;η为数据本底噪音。这里将电场E本底噪音取为10-15V/(A·m2),磁感应强度B本底噪音取为10-18T/(A·m)。对于模型的约束方式,使用最小梯度支撑约束(minimum gradient support,MGS)[34],与常用的光滑约束相比,MGS允许反演中模型参数的剧烈变化,可以获得更清晰的电性边界。
在高斯-牛顿反演中采用如下的迭代格式:
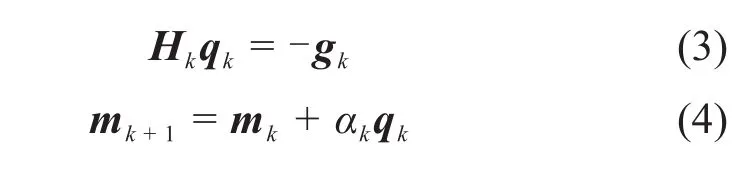
式中:gk为目标函数的梯度向量;Hk为目标函数的海森矩阵;qk为模型更新量;αk为步长;k为当前迭代次数。gk和Hk分别具有以下形式:
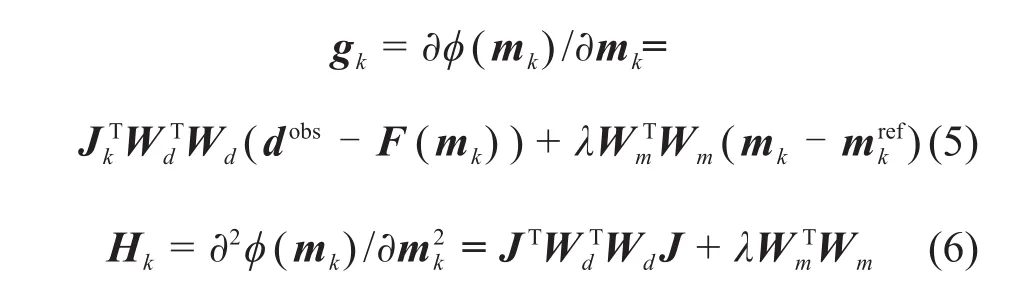
式中:Jk= ∂F(mk)/∂lgρ,为雅可比矩阵(或称灵敏度矩阵),可由解析公式给出[30]。步长αk采用基于Wolfe条件的非精确线搜索方法选取[32]。
正则化参数λ的选取是反演中的关键,本文采用NEWMAN等[14]提出的经验公式来计算第k次迭代的λ:

式中:anj为矩阵[(WdJ)T(WdJ)]中的元素。
在反演过程中,为使得模型参数m在合理范围内,采用非线性变换来约束模型参数[35-36]。
1.2 特征参数分析方法
特征参数分析(engenparameter analysis)是分析反演数据分辨能力的有效手段[26-29]。设模型参数向量为m,对应正演响应向量为F(m),对其添加一定误差e得到理论观测数据f(m)=F(m)+e。在考虑观测误差的情况下,一阶Taylor近似下正演响应与模型参数的关系可近似为,

式中:J为雅可比矩阵。SCHOLL等[27]指出,对于广义线性反演算法(如高斯-牛顿算法和共轭梯度算法等),通过一阶Taylor级数展开可将非线性反演问题线性化,仅当模型参数变化量∂m较小时,f(m)与m才可近似为线性关系。为便于特征参数分析,将f(m)和m均转换到对数域[26],即
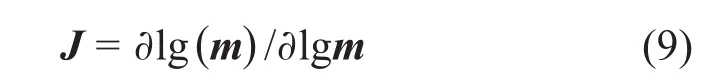
LANG[37]给出复数的对数形式:
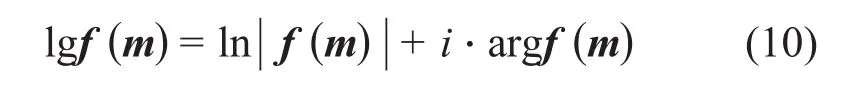
式中:i为虚数单位。考虑到
将式(10)代入式(9)经过转换,可得到:

对理论模型所对应的雅可比矩阵进行特征值分解(SVD)可得:

式中:数据矩阵U为Nd×Nm的酉矩阵(即有UT=U-1);S为Nm×Nm阶的对角阵;V为Nm×Nm的酉矩阵;Nd和Nm分别为观测数据和模型参数个数。S包含雅可比矩阵J的特征值(Eigenvalues),数据矩阵V包含雅可比矩阵J的特征参数(Eigenparameters)。将式(12)代入式(8)可得
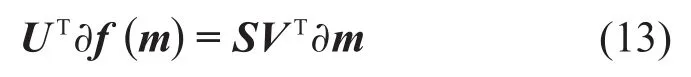
EDWARDS[26]指出,式(13)可用于分析实际数据的特征参数的误差,即

这说明特征参数的误差为对应特征参数的倒数,且模型参数的误差上限可用下式估算:
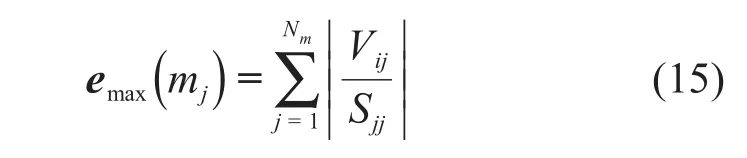
式中:i=1,…,Nd。
使用特征参数可定量分析反演数据对反演参数(一维情况下为地层电阻率等)的耦合性,以此为依据确定地层电阻率等在反演中能否重构[27]。
2 合成数据反演
采用经典的海洋一维油气储层模型进行测试[25]。图1所示为海洋一维油气储层模型示意图。由图1可见:该模型分5层,在海底地层中存在100 m高阻薄储层;在离海底上方50 m处沿y方向均匀布设41个水平电偶源,间距500 m(发射源坐标为xs=0 m,ys=0~20 km,zs=950 m),在海底布设1个接收站(x=y=0 m,z=1 000 m)。假定发射电流为1 A。理论模型正演数据(电场和磁场分量)的实部和虚部分别添加高斯随机噪音作为观测数据进行反演。初始模型采用海底电阻率为1 Ω·m的均匀半空间模型。反演时空气层和海水层电阻率和厚度固定,因此,在最终反演结果中空气层和海水层将不再显示。下面分别讨论电磁场分量的选择、频率的选择及观测模式对反演的影响。
2.1 电磁场分量的影响
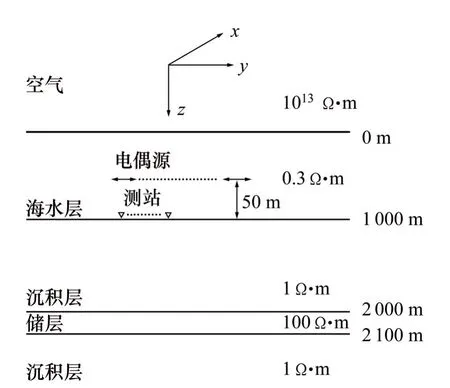
图1 海洋一维油气储层模型示意图Fig.1 1D canonical reservoir model
以海洋CSEM施工中常用的轴向观测模式为例,y方向电偶源产生水平电场分量Ey,垂直电场分量Ez和水平磁场分量Bx。常规频率域海洋CSEM反演以轴向观测模式下的单频轴向电场分量(Ey)反演为主[24]。本节将对使用单分量数据和同时使用Ey,Ez和Bx这3个分量数据的反演结果进行对比,所用发射频率为0.3 Hz和1.0 Hz。合成数据使用电磁场分量的实部和虚部,并加入2%的高斯随机噪声。图2所示为不同磁场分量合成数据反演结果。由图2可见:仅使用1个分量数据进行反演时,不但反演得到的高阻薄层厚度过大,且高阻薄层的位置有明显偏移,同时在浅层和深层出现明显虚假异常;使用3个分量数据进行反演时,反演结果得到改善,高阻薄层的埋深、厚度和电阻率范围均得到较好还原,但在浅层和深层仍存在明显虚假异常,这可以通过特征参数分析方法加以解释。

图2 不同电磁场分量合成数据反演结果Fig.2 Inversion of synthetic data using different electric and magnetic components
对于如图1所示的5层测试模型,在空气层和海水层已知的情况下,需要反演的海底地层参数共有3个(海底从上至下3层介质的电阻率ρ1,ρ2和ρ3)。图3所示为不同电磁场分量情况下特征参数分析结果,其中横坐标为特征参数(用P表示)序号,纵坐标为要反演的模型参数m(电阻率以10为底的对数)序号,对应的特征参数值以圆圈给出,白圆代表正特征参数,黑圆代表负特征参数,圆半径对应相对数值。由于V是酉矩阵,故特征参数绝对值不超过1,图例中给出圆圈大小对应单位值(1对应白圆,-1对应黑圆)。
SCHOLL等[27]指出,不同模型参数对应的特征参数P表征模型参数的耦合程度,P越大,则该模型参数解耦性越好。从图3(a),(b)和(c)可以看出,前2个特征参数P1和P2对应ρ1和ρ2,并且耦合在一起,说明使用单分量数据反演难以将ρ1和ρ2区分开;而第3个特征参数P3对应ρ3并且与P1和P2是解耦的,但是P3对应特征值均不超过1,这说明使用单分量数据难以反演出ρ3。从图3(d)可以看出:P1和P2分别对应ρ2和ρ1,而P3对应ρ3,P1和P2仍然耦合在一起,但与单频情况相比,耦合程度要弱;P3与P1和P2是解耦的,P3对应特征值为1.70。这说明使用3分量数据时反演结果要优于单分量数据反演结果。
2.2 频率的影响
反演所用合成数据使用Ey,Ez和Bx的实部和虚部并加入2%高斯随机噪声。图4所示为不同频率合成数据的反演结果,数据拟合差均接近1。
由图4(a)和(b)可见:使用单频率(0.3或1.0 Hz)进行反演时,反演得到的高阻薄层厚度过大,且高阻薄层的位置有明显下移,同时在浅层和深层出现明显虚假异常。由图4(c)可见:使用2个频率(0.3和1.0 Hz)进行反演时,高阻层的埋深和厚度得到较好还原,但浅层和深层仍有明显虚假异常。由图4(d)和(e)可见:使用3个频率(0.1,0.3和1.0 Hz)或使用4个频率(0.1,0.3,1.0和3.0 Hz)进行反演时,高阻层的埋深和厚度在得到较好还原的同时,浅层和深层的虚假异常得到较好压制,尤其是使用4个频率数据反演的结果更优。
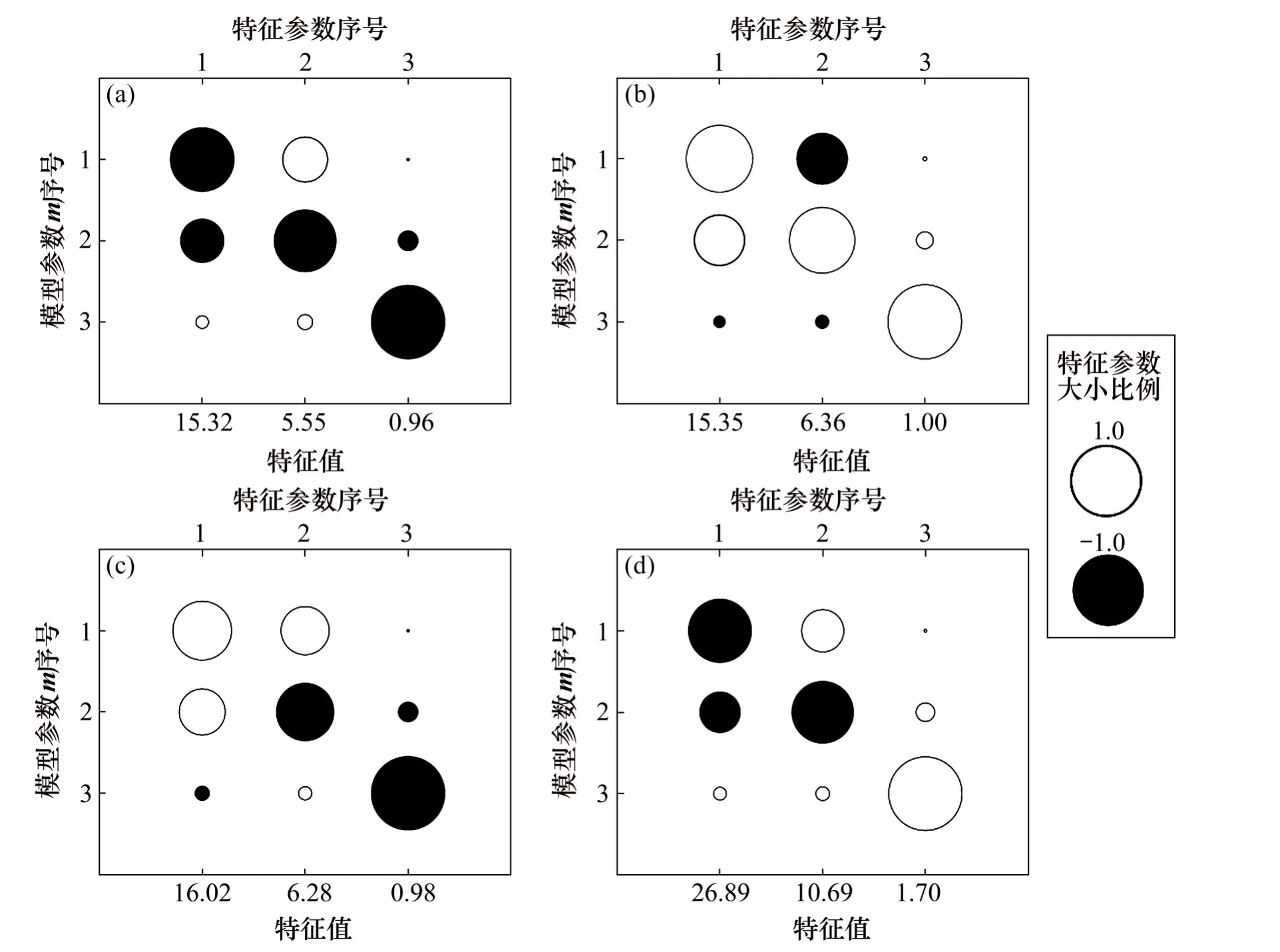
图3 不同电磁场分量情况下特征参数分析结果Fig.3 Engenparameter analysis for synthetic data using different electric and magnetic components
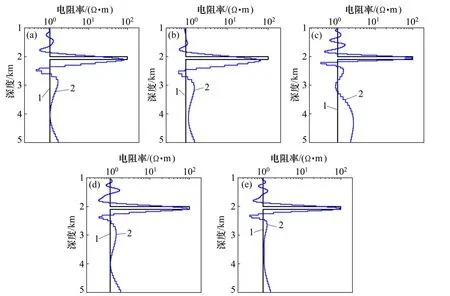
图4 不同频率合成数据反演结果Fig.4 Inversion of synthetic data using different frequencies
图5所示为多频率情况下特征参数分析结果。从图5(a)和(b)可以看出:前2个特征参数P2和P1对应ρ1和ρ2,并且耦合在一起,说明使用单频数据反演难以将ρ1和ρ2区分开;第3个特征参数P3对应ρ3并且与P1和P2是解耦的,但是P3对应特征值较小,这说明使用单分量数据难以反演出ρ3。由图5(c)可见:使用2个频率时特征参数分析结果是类似的,前2个特征参数P1和P2(对应ρ1和ρ2)耦合在一起,P3(对应ρ3)对应特征值较小,反演时难以区分ρ3。从图5(d)和图5(e)可以看出:P1,P2和P3(分别对应ρ2,ρ1和ρ3)是解耦的,这说明使用3个或4个频率反演时可以较好还原ρ2,ρ1和ρ3,且使用4个频率的特征参数解耦性最好。由此可知,在合适的频率范围内,适当增加频点个数可有效改善反演结果。
2.3 观测模式的影响
在频率域海洋CSEM勘探中,常使用轴向观测模式采集数据。下面对比单一观测模式(轴向观测模式inline或赤道观测模式broadside)合成数据和混合观测模式(轴向观测模式+赤道观测模式)下合成数据反演结果。发射频率为0.1,0.3,1.0和3.0 Hz,合成数据使用电磁场分量实、虚部并加入2%高斯随机噪声。轴向观测模式下电磁场分量Ey,Ez和Bx参与反演,赤道观测模式下电磁场分量Ex,By和Bz参与反演,混合观测模式下电磁场6个分量均参与反演。
图6所示为不同观测模式下合成数据的反演结果。从图6可以看出:赤道观测模式数据反演所得高阻层的位置相对真实模型向上有所偏移(图6(b)),这与CONSTABLE[2]的结论是一致的,与轴向观测模式情况相比,赤道模式数据对地下电性结构敏感性较差、恢复能力差,因此,在频率域海洋CSEM勘探中常使用轴向观测模式采集数据。轴向观测模式或混合观测模式数据反演结果较好,且混合观测模式下浅层和深层的电阻率更接近真实值。
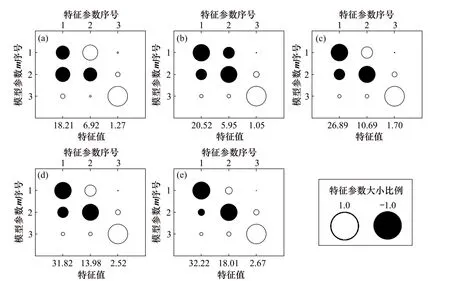
图5 不同频率情况下特征参数分析结果Fig.5 Engenparameter analysis for synthetic data using different frequencies
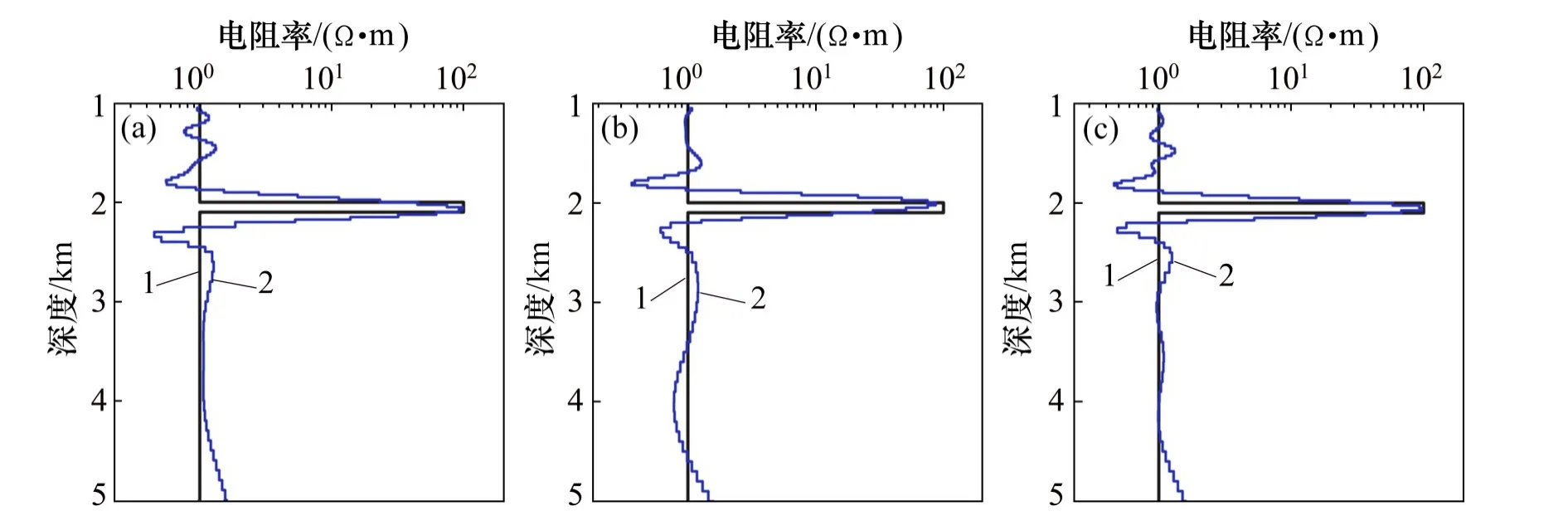
图6 不同观测模式下合成数据反演结果Fig.6 Inversion of synthetic data using different survey geometries
图7所示为不同观测模式下特征参数分析结果。由图7可见:赤道观测模式下特征参数的解耦性较差,而在轴向观测模式和混合观测模式下,特征参数的解耦性较好,且混合模式下特征参数耦合程度最低,表明混合观测模式数据反演效果最好。
3 实际数据反演
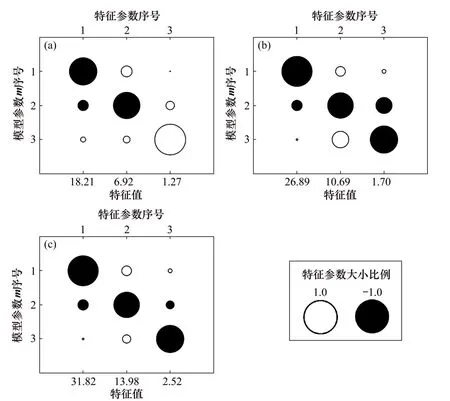
图7 不同观测模式下特征参数分析结果Fig.7 Engenparameter analysis for synthetic data using different survey geometries
下面对挪威Troll油田的实际数据进行反演试算。取实测数据某一测线进行测试[38],该测线区海底地形起伏较小,平均水深约330 m,测线长约18 km,其中46个发射源离海底约30 m深度处,接收站位于海底。发射频率包括0.25,0.75和1.25 Hz。选取某一接收站处采集的水平轴向电场分量进行反演(在此次海试中,只有水平轴向电场分量有效,因此,暂时无法进行多分量数据反演)。初始模型为海底半空间模型(电阻率为1 Ω·m),其中空气层和海水层在反演中固定。
图8所示为Troll油田实际数据反演结果,最终数据的拟合差为1.60。图8中虚线对应地震资料所确定的高阻油气层的顶部埋深,反演所得高阻层埋深与地震资料分析结果非常接近。图9所示为观测电场分量数据与反演得到电场分量数据拟合情况,从图9可以看出:3个频率下观测数据与反演所得的电场分量数据拟合较好。
根据MORTEN等[38]的反演结果,并结合图8,将此测点处地下电性结构简化为1个5层模型(包括空气层和330 m厚海水层),其中从深度1 500 m起是厚度为200 m,电阻率为60 Ω·m的高阻储层,储层上方是厚度为1 270 m,电阻率为1 Ω·m沉积层,储层下方沉积层的电阻率为1 Ω·m。根据特征参数分析方法,可得此简化模型对应的特征参数分析结果,如图10所示。从图10可以看出:P1对应于ρ2和ρ3,P2对应于ρ1和ρ3,P3对应于ρ1和ρ2的值非常小,说明这3层的模型参数是解耦的,对所使用的数据进行反演,理论上可以将3层区分开来;另一方面,P3对应的特征值较小,反演在理论上难以还原出第3层的真实电阻率,根据前面理论模型的测试结果,这有可能是仅使用了单一观测模式、单一电磁场分量的数据造成的。尽管如此,此简化模型对应的特征参数的解耦性较好,能在一定程度上说明图8所示反演结果是可靠的。根据式(15)可以估算出此简化模型参数的误差上限为|V11/S11|+|V12/S22|+|V13/S33|=4.95%。
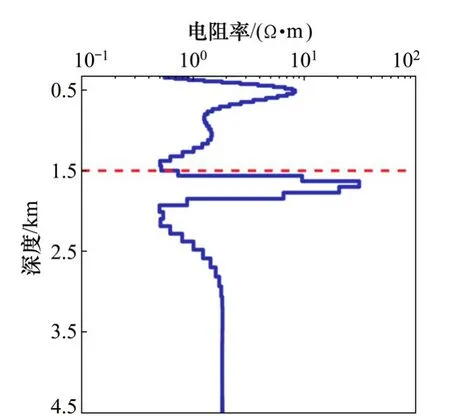
图8 Troll油田实际数据反演结果Fig.8 Inversion of Troll field data
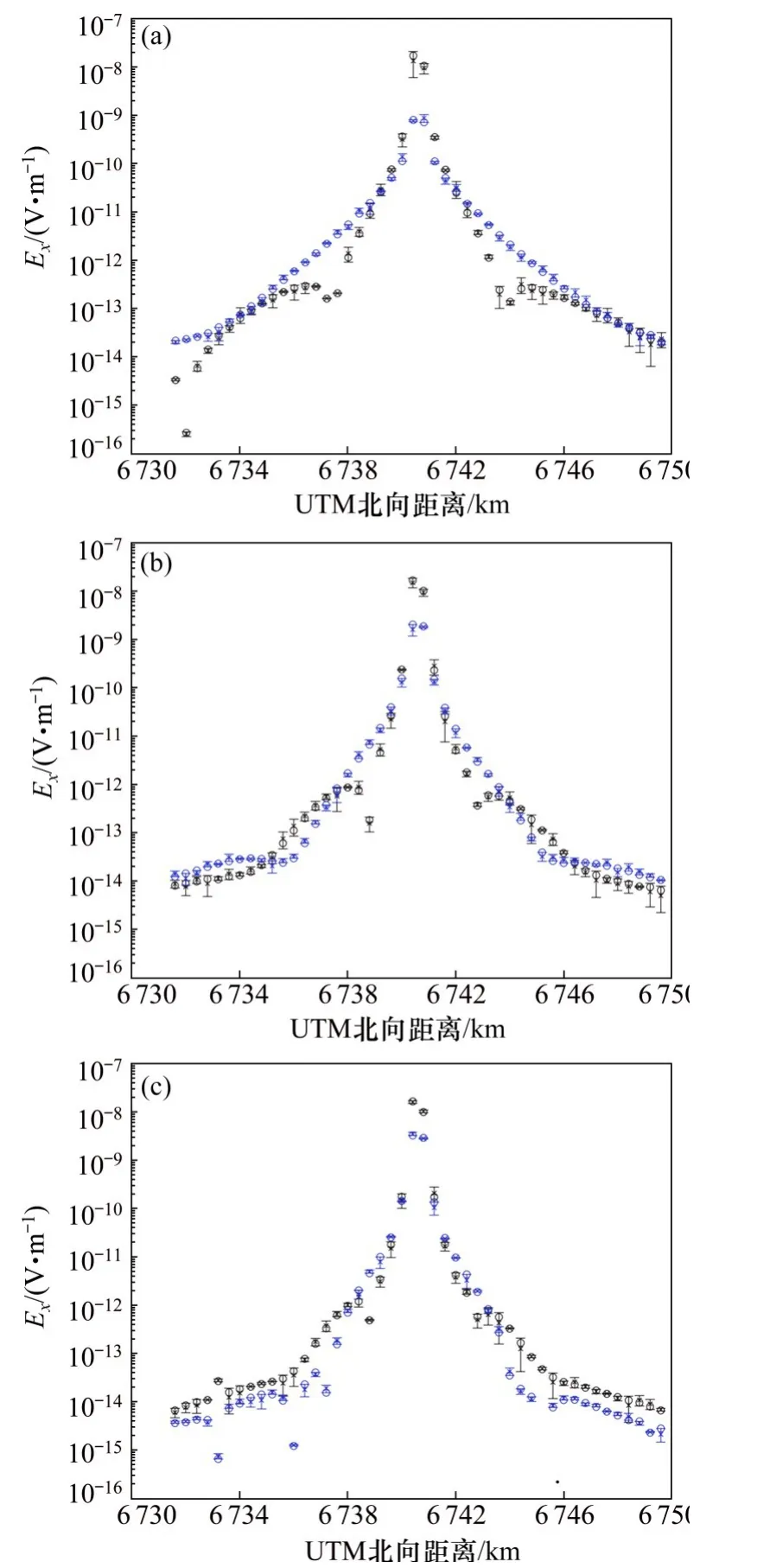
图9 观测电场分量数据与反演得到电场分量数据拟合情况Fig.9 Data fitting between observed electric data and calculated electric data
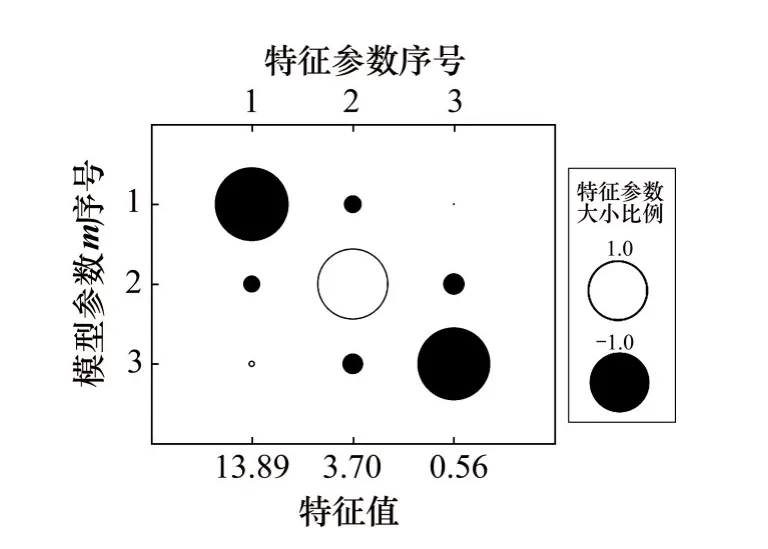
图10 Troll油田一维简化模型对应的特征参数分析结果Fig.10 Engenparameter analysis for reduced ID model obtained from Troll field data
从该实际数据反演算例可知:使用特征参数分析方法可对实际数据质量进行评价,在对实际数据进行大规模二维或三维反演前,可结合测区已知地质钻井资料建立1个反演初始模型,使用该模型对实际数据进行特征参数分析,可初步推断该数据是否适合反演。
4 结论
1)反演时恰当地选择电磁场分量、观测模式以及频率可明显改善反演效果,通过特征参数分析方法可以在一定程度上评估这几个因素的选择是否合理。
2)利用所开发的反演算法对挪威Troll油田的实际CSEM数据反演所得到的电阻率模型与地震资料的解释结果吻合,进一步证明了反演算法的有效性。
3)建立了1个简化的5层模型,对该简化模型进行特征参数分析,结果表明特征参数分析方法可应用于实际资料的反演。
4)在对实际数据进行大规模二维或三维反演前,结合测区已知地质钻井资料可建立1个反演初始模型,使用该模型对实际数据进行特征参数分析,可初步判断该数据是否适合反演。
