基于响应面法和正交试验的涡轮流量计优化设计

张晓东 李 谨 龚 彦

(西南石油大学 机电工程学院， 成都 610500)

引 言

涡轮流量计具有精度高、重复性好、结构简单、测量范围广、体积小、质量轻、压力损失小、维修方便等优点，但存在性能会随被测流体黏度增大而变差的问题[1-2]。目前，国内的涡轮流量计在出厂时，其性能一般都是用水或黏度比较低的柴油进行鉴定，但很多使用者却用涡轮流量计来测量液压油、润滑油等中黏度甚至高黏度液体的流量，导致出现很大的测量误差。因此，提高涡轮流量计在测量黏性介质时的精度具有非常重要的现实意义。

目前关于黏性介质对涡轮流量计影响的研究主要集中在分析流量计内部几何结构和流体介质对其性能的影响[3-7]以及仪表系数的修正方法[8-9]等方面，而根据流体性能对流量计进行结构优化的研究较少，在结构优化时考虑到内部几何参数间交互作用的则更少。由于涡轮流量计几何参数较多，作用的机理各不相同，各个参数之间存在交互作用，因此有必要研究各个参数间的相互关系，确定最优参数组合。本文以DN40涡轮流量计为例，从优化几何结构出发，探究几何参数对涡轮流量计性能的影响，分析显著影响因素之间的交互作用，并在计算流体力学(CFD)仿真的基础上通过响应面法和正交试验对结构进行优化设计。

1 模型与仿真

1.1 模型的建立

选择某公司生产的LWGY 系列 DN40涡轮流量计，其主要参数为：叶轮叶片数N1=6，叶片顶端半径Rt=9.5 mm，叶轮轮毂半径Ro=10 mm，叶轮轮毂长度Lh=8 mm，叶轮导程L=88.5 mm，导流体叶片数N2=4，前导流体轮毂长度H1=54 mm，后导流体轮毂长度H2=38 mm。

按照上述几何参数建立三维模型，如图1所示。为了使流体接近充分发展状态从而形成稳定的流速分布，在涡轮流量计前后分别加装10D和5D长直管段[10]。

图1 涡轮流量计三维模型Fig.1 3D model of the turbine flowmeter

1.2 网格划分

将三维模型导入网格划分软件ICEM中，考虑到流量计叶轮部分和导流件部分结构复杂，而且是仿真计算的关键部件，因此在ICEM中均采用非结构化的四面体网格对叶轮流域和导流件流域进行划分；而前、后直管段流域结构相对简单但尺寸较大，采用四面体网格划分会使网格数量大大增加，为了减少仿真时间，采用结构化的六面体网格对该流域进行划分，划分后的网格数为1 474 621个，其Quality最小值为0.36。通过增加整体网格数进行网格无关性检验，网格尺度符合计算要求。

1.3 边界条件定义

边界条件如下：

(1)仿真介质采用实际状况下的原油，其运动黏度为2.64×10-5m2/s，密度为887 kg/m3，流量范围2～20 m3/h；

(2)入口采用速度入口，选取2 m3/h、4 m3/h、8 m3/h、14 m3/h、20 m3/h这5个体积流量下的入口速度；出口采用压力出口，设置为1个标准大气压；

(3)管壁，上、下导流体和叶轮表面均采用无滑移壁面边界条件；

(4)涡轮流量计叶轮部分流域设置为旋转流域，前后导流件部分设置为固定流域，旋转流域与固定流域之间采用交界面进行连接。

1.4 湍流模型的选择

由于涡轮流量计叶轮在流体中处于高速旋转状态，其表面曲率变化非常大，而雷诺应力模型(RSM)考虑到了流体旋转或流线弯曲所带来的应力张量的急剧变化，可以更好地模拟涡轮流量计在复杂流场状况下的运行规律，因此本文选用RSM湍流模型[11]。

1.5 仿真仪表系数和线性度误差的计算

仪表系数为涡轮感应放大器产生的脉冲数与流过传感器流体体积的比值[12]。在计算仿真仪表系数之前需要计算流量计叶轮在该流量下的稳定转速θ。通过监测发现，当叶轮驱动力矩与阻力矩的差值小于10-8时，可认为叶轮所受力矩达到平衡，则此时的叶轮转速即为稳定转速。叶轮稳定转速确定后，根据叶片个数、入口流速与管道截面积可以得到此时的涡轮流量计仿真仪表系数，其计算公式为

(1)

式中，K为涡轮流量计仿真仪表系数，L-1；N为叶轮叶片个数；θ为叶轮稳定转速，rad/s；V为入口流速，m/s；A为前直管段入口截面积，m2。

仪表系数线性度误差可以反映涡轮流量计的测量精度，仪表系数线性度误差越小，则流量计的测量精度越高，反之则测量精度越低。

通过式(1)计算出2 m3/h、4 m3/h、8 m3/h、14 m3/h、20 m3/h这5个点的仿真仪表系数后，便可以得到涡轮流量计仪表系数线性度误差δ，其计算公式为

(2)

式中，Kmax,i为流量计在5个流量点处得到的仪表系数最大值；Kmin,i为流量计在5个流量点处得到的仪表系数最小值。

2 Plackett- Burman设计

根据Plackett- Burman(PB)试验设计，选取8个试验因素(叶轮顶端半径、叶轮叶片数、叶轮轮毂半径、叶轮轮毂长度、叶轮导程、前导流件长度、后导流件长度、导流体叶片数)和3个空白因素，每个因素设高、低两个水平，以仪表系数线性度误差为响应值，共计12个试验，试验设计因素及水平见表1。

表1 PB设计因素与水平

对表1试验中各因素进行显著性分析，分析结果如表2所示，模型显著差异水平p=0.004，说明回归方程关系显著；决定系数R2=0.992 7，说明回归有效，试验结果可靠。由表2还可以看出8个因素均对流量计线性度误差影响显著，其中叶轮叶片数N1、叶轮顶端半径Rt、叶片轮毂半径Ro、叶轮轮毂长度Lh这4个为显著影响参数，在后文中运用响应面法进行优化；而叶轮导程L、前导流件长度H1、后导流件长度H2、导流体叶片数N2这4个为次显著影响参数，在后文中运用正交试验进行优化。

表2 参数显著性分析

3 结构参数优化

3.1 显著影响参数的响应面法优化

采用Box- Behnken中心组合设计方法，以叶轮顶端半径Rt、叶片数N1、叶片轮毂半径Ro、叶轮轮毂长度Lh这4个显著影响因素为自变量，仪表系数线性度误差为响应值，其余结构参数保持不变，设计四因素三水平29个试验点的响应面优化试验。因素与水平见表3，试验设计见表4。

表3 Box- Behnken设计因素与水平

对模型进行方差分析得到的响应面分析结果如表5所示，p<0.000 1<0.05，表明该模型是显著的，具有统计学意义。由表5数据可得，自变量Rt、N1、Ro、Lh均显著(p<0.05)，按照对响应值的影响程度排序为叶轮顶端半径Rt>叶轮叶片数N1>叶轮轮毂长度Lh>叶轮轮毂半径Ro。失拟项P=0.056>0.05，此值不显著，说明在试验范围内预测值和实测值的拟合度较高，能够选择该回归方程对试验结果进行相关分析，线性度误差R的回归方程为

表4 Box- Behnken设计结果

表5 Box- Behnken设计方差分析

图2 影响仪表系数线性度误差的几何参数间交互作用Fig.2 Interaction of geometric parameters affecting the linearity error for instrument coefficients

从图2(a)～(f)可形象地看出影响仪表系数线性度误差的几何参数间交互作用。比较图2各个分图可知，叶轮顶端半径Rt对仪表系数线性度误差的影响最为显著，表现为曲线最陡，其余因素影响大小顺序为叶轮叶片数N1>叶轮轮毂长度Lh>叶轮轮毂半径Ro。这也与表5的方差分析结果相吻合。

使用Design Expert软件在表3变量的高低水平范围内寻优，以叶轮叶片数是整数为前提，取其中一个最优组合进行CFD仿真计算，并与显著因素的响应面回归方程预测值进行比较，比较结果如表6所示。可以看出，对于优化后的流量计模型，其仪表系数线性度误差拟合公式的预测值与CFD计算值非常接近，误差仅为0.6%，说明响应面法可以很好地用于涡轮流量计结构优化。

3.2 次显著影响参数的正交试验设计

在对显著参数进行响应面优化后，选择叶轮导程L、前导流件长度H1、导流体叶片数N2、后导流件长度H2这4个次显著影响因素为自变量，以流量计线性度误差为响应值进行正交试验设计，根据因素和水平数选择正交表L9(34)，一共9组仿真计算模型，因素与水平见表7。

正交试验结果与均值如表8所示，因素L对应的均值2最小，表明L取第二水平上的值时线性度误差最小，同理可以得到H1、N2和H2的取值分别为第三水平、第二水平和第二水平，因此理论上的最优水平组合为L2(H1)3(N2)2(H2)2。

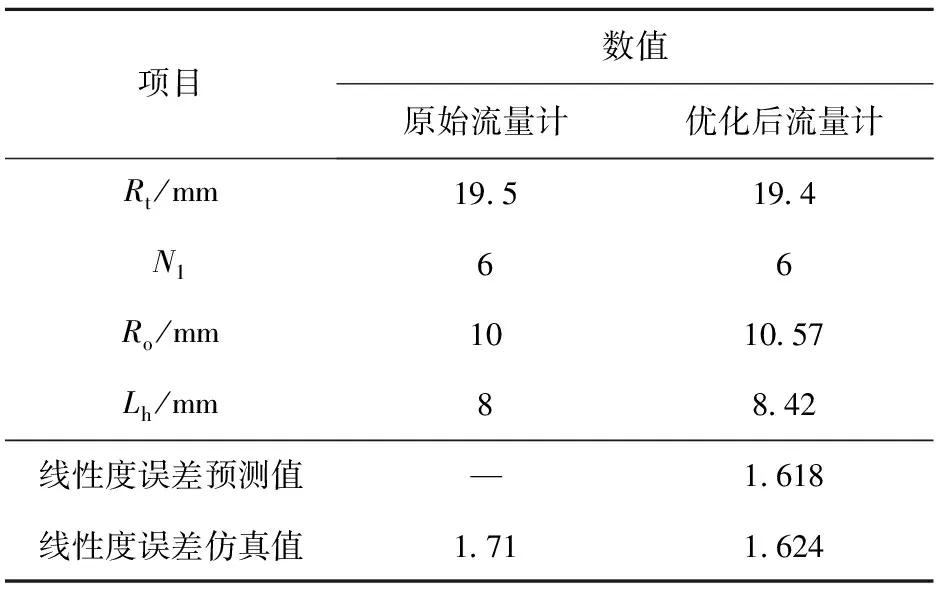
表6 响应面优化前后参数对比

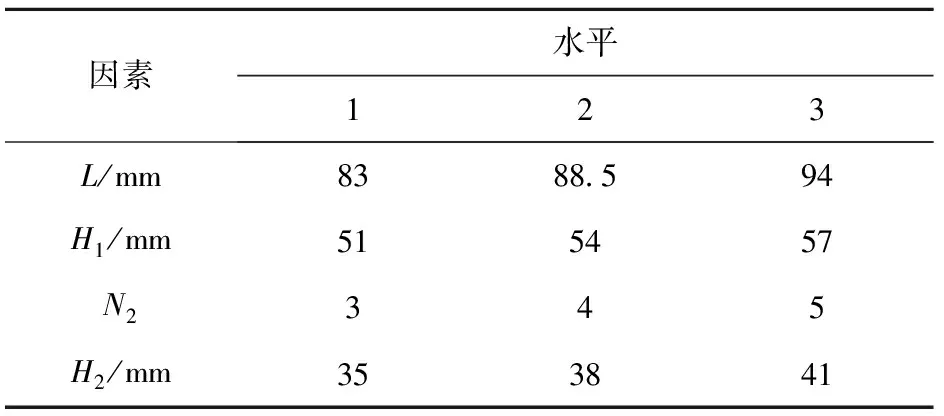
表7 正交试验因素与水平

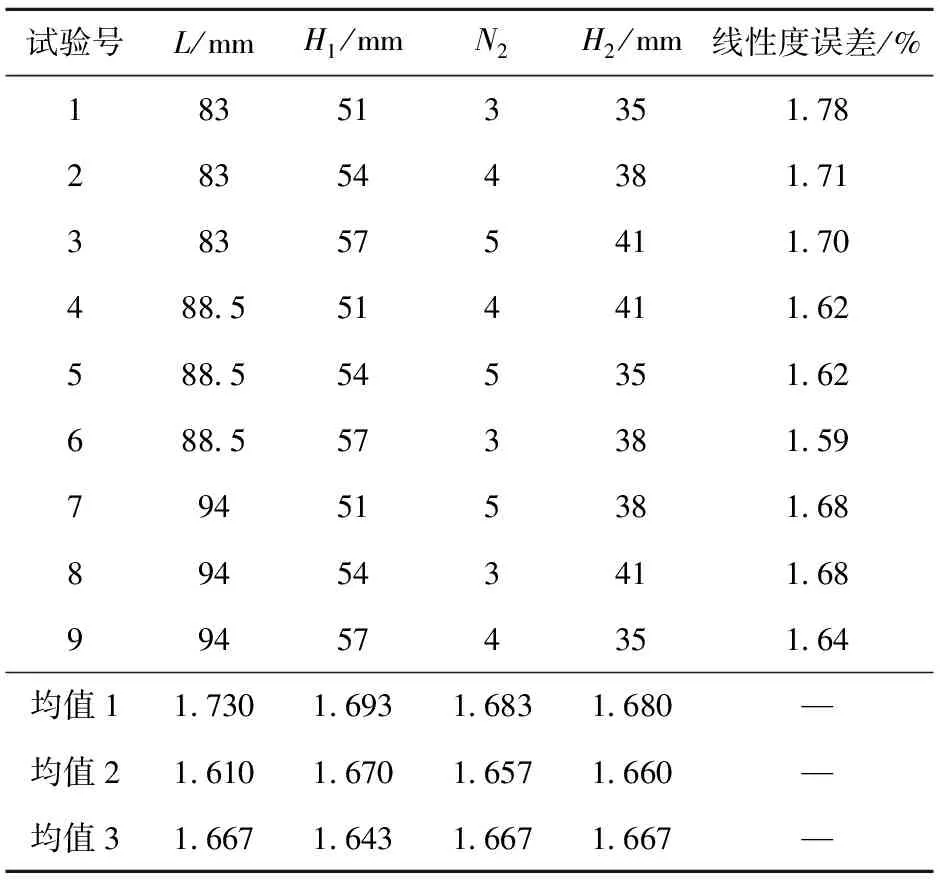
表8 正交试验结果与均值

图3和图4分别为原始流量计与优化后流量计的截面速度分布云图。对比图3和图4可以看出，优化后的流量计在后导流件上下部分的流场速度分布较原始流量计更加均匀，说明优化后流量计的叶轮结构在流场中的旋转稳定性更好，从而使得测量精度得到提高。

图3 原始流量计截面速度分布云图Fig.3 Velocity distribution cloud diagram for the original flowmeter section

图4 优化后流量计截面速度分布云图Fig.4 Velocity distribution cloud diagram for the flowmeter section after optimization

4 试验验证

图5 流量技术检测试验装置Fig.5 Flow detection test equipment

将优化前后的涡轮流量计在西南石油大学流量技术检测试验台上进行试验，试验装置如图5 所示。试验介质采用由机油和柴油按照一定比例混合的密度为887 kg/m3、运动黏度为2.64×10-5m2/s的混合液，采用静态容积法原理，利用泵为流体提供动力，流体经过流量控制阀和被测涡轮流量计后直接流回容积池中。分别选取2 m3/h、4 m3/h、8 m3/h、14 m3/h、16 m3/h、20 m3/h这6个体积流量点，通过计算机控制台采集每个流量点下试验流量计产生的脉冲个数N，从而得到涡轮流量计在6个流量点下的仪表系数K。试验中每个流量点分别进行3次重复性试验，试验误差均小于0.025%。

将原始流量计仪表系数与优化后的流量计仪表系数进行对比，结果如图6所示。流量计仪表系数CFD仿真值与试验值吻合，证明了CFD仿真的准确性。对比原始涡轮流量计和优化后涡轮流量计仪表系数试验值曲线得出，优化后的流量计在不同流量处的仪表系数变化情况较原来更为平稳。经计算，仪表系数线性度误差由原来的1.71%下降到了1.59%，显著提高了涡轮流量计的测量精度。

图6 流量点与仪表系数的关系Fig.6 Relationship between the flow point and instrument coefficient

5 结论

(1) Plackett- Burman设计分析表明，对涡轮流量计测量精度影响显著的参数为叶轮顶端半径、叶轮叶片数、叶轮轮毂半径和叶轮轮毂长度，影响次显著的参数有叶轮导程、前导流件长度、后导流件长度和导流体叶片数。

(2) 运用Box- Behnken设计方法对筛选出来的显著影响参数进行试验设计，建立了涡轮流量计线性度误差的多元回归模型，并检验了预测模型的拟合度。结果表明，回归模型对实际情况拟合较好，能够运用响应面法对涡轮流量计结构参数进行优化。

(3)在响应面法优化的基础上，对筛选出来的次显著影响参数进行正交试验设计，得到了最优结构组合。试验验证结果表明优化后的涡轮流量计测量精度得到了显著提高。