稀疏度自适应回溯追踪算法改进

丁佳静 武雪姣 李雪晴

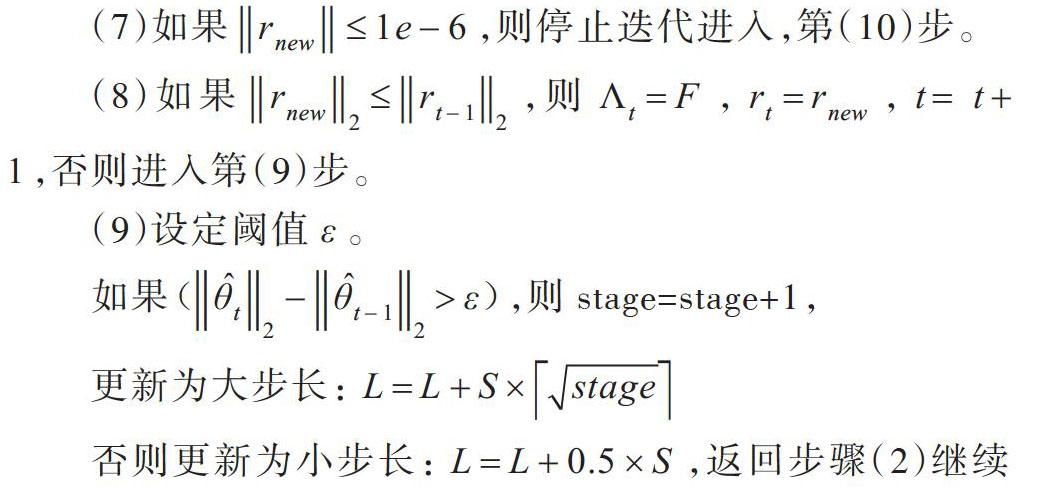
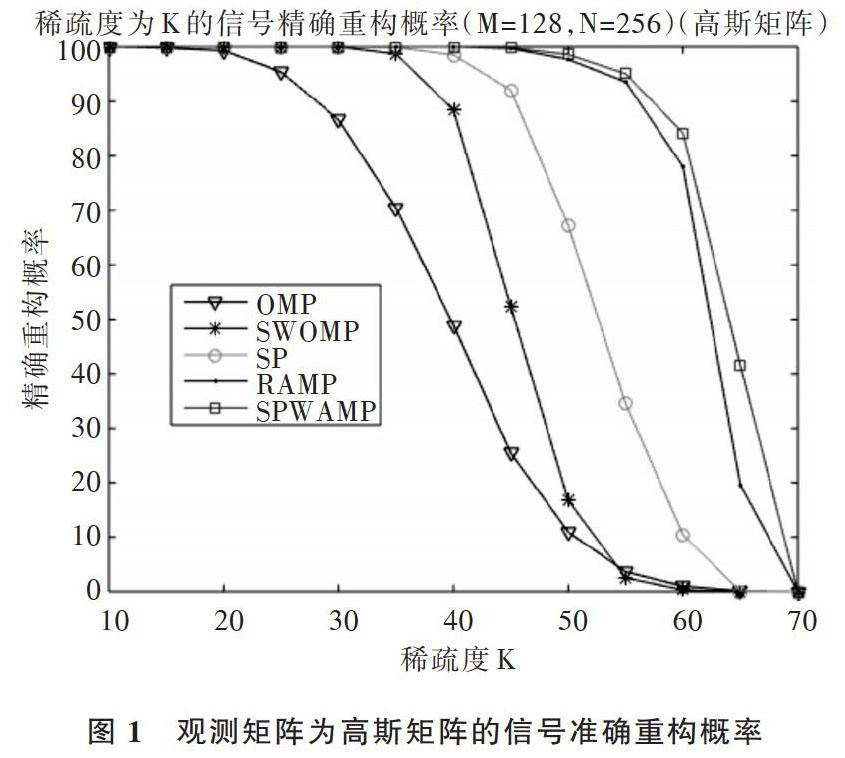
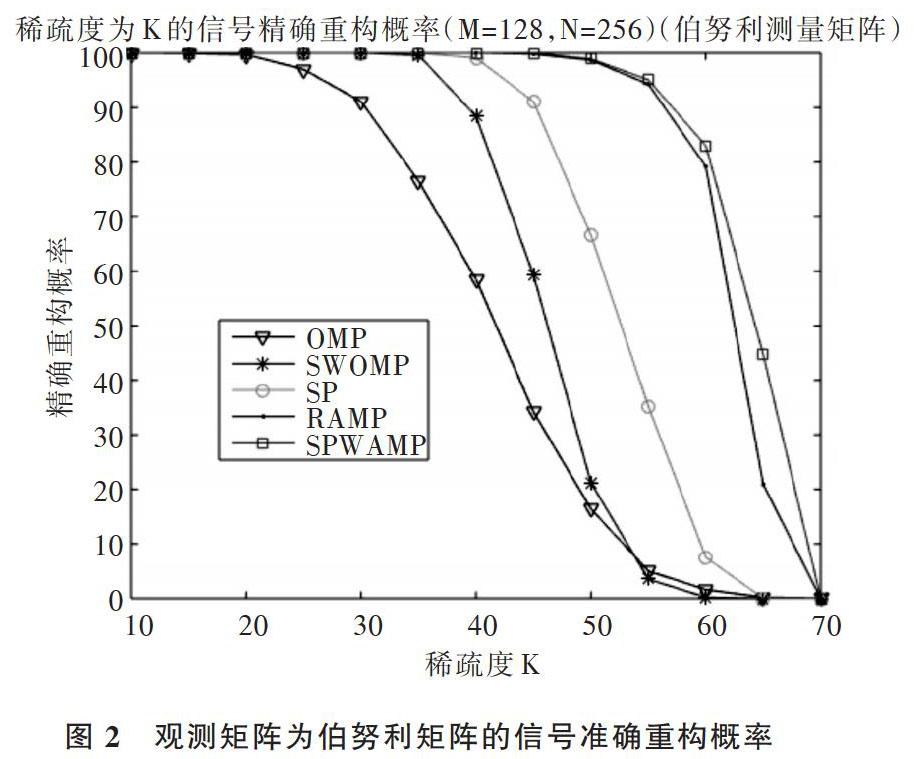
摘 要：针对压缩感知重构算法中信号稀疏度未知和步长大小固定的问题，提出一种新的压缩感知信号重构算法，即基于弱选择的稀疏度自适应回溯追踪（SPWAMP）算法。该算法将自适应思想、变步长迭代思想与回溯思想相结合，在未知信号稀疏度的情况下，利用阈值方法选取预选集，通过变步长更新支撑集原子个数并结合回溯思想剔除不可靠原子，最终实现信号精确重构。仿真结果表明，当信号稀疏度K达到65时，该算法重构精度相对稀疏度自适应匹配追踪（SAMP）算法提高了40%，而此时正交匹配追踪（OMP）算法、子空间追踪（SP）算法和分段弱选择正交匹配追踪（SWOMP）算法已无法实现重构。因此，该算法相对其它同类算法提高了信号重构精度。

关键词：压缩感知;重构算法;稀疏度自适应;信号处理

DOI：10. 11907/rjdk. 191437 开放科学（资源服务）标识码（OSID）：

中图分类号：TP312 文献标识码：A 文章编号：1672-7800（2019）008-0059-04

Improved Algorithm for Sparsity Adaptive Backtracking

DING Jia-jing， WU Xue-jiao， LI Xue-qing

（School of Information Engineering， Hebei GEO University， Shijiazhuang 050000， China）

Abstract：Aiming at the reconstruction of unknown sparsity signal and step size small fixed in compressed sensing， we put forward a new compression sensing signal reconstruction algorithm， namely sparsity adaptive backtracking algorithm based on weak selection（SPWAMP）. The algorithm combines the idea of adaptive， variable step iteration and backtracking. In the case of unknown signal sparsity，the preset is selected by threshold method， and the number of atoms in the support set is updated by variable step size and the idea of backtracking is used to eliminate the unreliable. Finally， the precise signal reconstruction is realized. Simulation results show that when the signal sparsity K reaches 65， the reconstruction accuracy of the algorithm is improved by 40% compared with SAMP， while OMP， SP and SWOMP cannot realize the reconstruction. Therefore， compared with other similar algorithms， this algorithm improves the signal reconstruction accuracy.

Key Words：compressed sensing; reconstruction algorithm; sparse degree adaptive; signal processing

作者簡介：丁佳静（1992-），女，河北地质大学信息工程学院硕士研究生，研究方向为人工智能与机器学习。

0 引言

2004年，Donoho[1]提出压缩感知（Conmpressed Sensing，CS）理论，指出如果信号在某个变换域是稀疏的，则可借用一个观测矩阵将变换后的信号降维;若该观测矩阵满足约束等距性条件，可以求解最优化问题，并根据低维测量向量，高概率地精确恢复原始信号。该理论在信号处理领域有广阔的应用前景[2-5]。

压缩感知理论主要由信号稀疏表示、测量矩阵构造和重构信号算法组成，其中，最核心的是重构算法[6-9]，其代表性算法包括正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法[10]、子空间追踪（Sub-space，SP）算法[11]、正则化正交匹配追踪（Regularized Orthogonal Matching Pursuit，ROMP）算法[12]、分段正交匹配追踪（Stagewise Orthogonal Matching Pursuit，StOMP）算法[13]和稀疏度自适应匹配追踪（Sparsity Adaptive Matching Pursuit，SAMP）算法[14]。2010年杨成等[15]提出一种新的稀疏度自适应子空间追踪算法，该算法在每次迭代中采用弱匹配原则选取新原子，并引入SAMP自适应思想，再通过回溯思想提高重构准确性;2013年Xue等[16]提出VSStAMP（Variable Step size Stagewise Adaptive Matching Pursuit）算法，该算法根据判断候选集中包含原子的个数作为变步长的标准，当原子个数小于u*M时采用大步长2*s，当原子个数小于u*M时采用小步长s。

本文在现有压缩感知重构算法的基础上，针对实际信号稀疏度大多未知及步长大小固定的问题，结合SP算法的回溯思想和SAMP算法的自适应思想，并运用弱匹配原则选取新原子和变步长思想，提出一种改进的基于弱选择的稀疏度自适应回溯追踪（Sparsity subspace Weak Adaptive Matching Pursuit，SPWAMP）算法。

1 压缩感知理论

压缩感知理论中待采样的信号能够实现压缩感知技术的前提是该信号是稀疏的，即利用信号可压缩性减少采样样本数目，且可以重建原始信号。压缩感知与普通采样率不同之处在于，测量对象不再是信号的某一采样点数据，而是一组用于描述信号的线性方程[17-18]。

假设待采样信号[x]的长度为[N]，观测信号[y]的长度为[M]（[M<

[y=Φx]                （1）

[x]一般不是稀疏的，但在某个变换域[Ψ]是稀疏的，即[x=Ψθ]。此时[y=ΦΨθ]，令[A=ΦΨ]，则[y=Aθ]。其中[θ]表示[K]是稀疏的，即[θ]只有[K]个非零项，是信号[x]在某变换域的系数表示，[Φ]是大小为[M×N]的测量矩阵，[Ψ]是大小为[N×N]的稀疏矩阵，[A]是大小为[M×N]的传感矩阵。

根据观测值[y]，利用稀疏重构关系和重构算法重构信号[x]，可求解[l1]范数优化问题：

[minαα1s.t.y=Ax]        （2）

从观测值[y]中恢复稀疏系数[θ]，进而求出信号[x]的精确估计[19-20]。

2 基于弱选择的稀疏度自适应回溯追踪算法

压缩感知中子空间追踪（SP）算法在每次迭代中选择多个原子，利用回溯思想，在每次迭代过程中重新估计所有候选者的可信赖性，但其自身也有不足，必须以稀疏度作为输入参数。

2.1 SP算法

SP 算法核心步骤：

输入：[M×N] 传感矩阵[A]

[N]維观测向量[y]

信号稀疏度[K]

（1）初始化[r0=y，Λ0=φ，A0=φ，t=1]。

（2）计算内积[u=abs[ΑTrt-1]]（即计算[rt-1，aj]，[1][jN]），选择[u]中[K]个最大值，将这些值对应[Α]的列序号[j]构成集合[J0]（列序号集合）。

（3）令[Λt=Λt-1？J0]，[Αt=Αt-1？aj][（j∈J0）]。

（4）从[θt]中选出绝对值最大的[K]项记为[θtK]，对应[At]中[K]列记为[AtK]，对应[A]的列序号记为[ΛtK]，更新集合[Λt]=[ΛtK]。

（5）求[y=Αtθt]的最小二乘解：[θt=argminθ||y-Αtθt||=][（ΑTtAt）-1ATty]。

（6）更新残差，使得[rt=y-ΑtKθtK=y-ΑtK（ΑTtKΑtK）-1][ΑTtKy]。

（7）[t=t+1]，如果[t≤S]则返回第（2）步继续迭代，如果[t>S]或残差[rt=0]则停止迭代进入。

（8）重构得[θ]在[ΛtK]处有非零项，其值分别为最后一次迭代所得[θtK]。

输出：信号稀疏表示系数估计[θ]

[N×1]维残差[rS=y-ASθS]

2.2 SPWAMP算法

本文算法在SP算法的基础上，采用弱匹配原则选取新原子，结合SAMP算法自适应思想在迭代过程中自动调整所选原子数目，并采用变步长提高信号重构精度[21]。当算法在开始执行时采用大步长快速接近（使用幂函数变步长），当接近目标时，采用小步长（步长为原步长的0.5倍），并且通过相邻信号能量之间的关系作为改变步长的标准。

总之，基于弱选择的稀疏度自适应回溯追踪（SPWAMP）算法是一种结合SP算法的回溯思想和SAMP算法的自适应思想，并通过弱匹配原则选取新原子和变步长思想的新重构算法，提高了算法重构精度。

SPWAMP 算法核心步骤为：

输入：[M×N]的传感矩阵[A=ΦΨ]

[N×1]  维观测向量[y]

步长[S]

（1）初始化[r0=y，Λ0=φ，L=S，t=1]。

（2）计算[u=abs[ΑTrt-1]]（即计算[rt-1，aj]，[1jN]），选择[u]中[L]个最大值，将这些值对应[Α]的列序号[j]构成集合[Sk]（列序号集合）;选择[u]中大于门限[Th]的值，将这些值对应A的列序号[j]构成集合[J0]（列序号集合）。

（3）令[Ck=Λt-1？Sk？J0][Αt={aj}][（for  all  j∈Ck）]。

（4）求[y=Αtθt]的最小二乘解：[θt=argminθ||y-Αtθt||=][（ΑTtAt）-1ATty]。

（5）从[θt]的中选出绝对值最大的[L]项记为[θtL]，对应的[At]中的[L]列记为[AtL]，对应的[A]的列序号记为[ΛtL]，更新集合[F]=[ΛtL]。

（6）更新残差，使得[rnew=y-ΑtL（ΑTtLΑtL）-1ΑTtLy]。

（7）如果[rnew≤1e-6]，则停止迭代进入，第（10）步。

（8）如果[rnew2≤rt-12]，则[Λt=F]，[rt=rnew]，[t=][t+][1]，否则进入第（9）步。

[9] 刘浩强，赵洪博，冯文全. 基于CS的正则化稀疏度变步长自适应匹配追踪算法[J]. 北京航空航天大学学报，2017，43（10）：2109-2117.

[10] TROPP J A，GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Transactions on Information Theory，2007，53（12）：4655-4666.

[11] WEI D， MILENKOVIC O. Subspace pursuit for Compressive Sensing signal reconstruction[J].  IEEE Transactions on Information Theory， 2009， 55（5）：2230-2249.

[12] NEEDELL D，VERSHYNIN R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit [J]. IEEE Journal of  Selscted Toptics in Signal Processing，2010，4（2）：310-316.

[13] DONOHO D L，TSAI G Y，STARCK J L. Sparse solution of under-determined linear equations by stage-wise orthogonal matching pursuit [J]. IEEE Transactions on Information Theory，2012，58（2）：1094-1121.

[14] DO  T  T，GAN L， NGUYEN N，et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing [C]. Piscataway：IEEE Conference on Signals，2008.

[15] 楊成，冯巍，冯辉，等. 一种压缩采样中的稀疏度自适应子空间追踪算法[J]. 电子学报，2010，38（8）：1914-1917.

[16] XUE B I， CHEN X D， ZHANG Y U. Variable step size stagewise adaptive matching pursuit algorithm for image compressed sensing[C]. 2013 IEEE International Conference on Signal Processing， Communication and Computing，2013：1-4.

[17] 王烈，罗文，秦伟萌. 分段弱选择自适应正交匹配追踪算法[J]. 计算机工程与设计，2018，39（12）：3767-3773.

[18] 王福驰，赵志刚，刘馨月，等. 一种改进的稀疏度自适应匹配追踪算法[J]. 计算机科学，2018，45（S1）：234-238.

[19] 王欣，张严心，黄志清. 基于变步长的正则化回溯自适应追踪算法[J]. 电子学报，2018，46（8）：1829-1834.

[20] 杨韧，张兴敢. 压缩感知重构SAMP的改进算法[J]. 南京大学学报：自然科学版，2018，54（3）：538-542.

[21] 彬彬有礼的专栏. 压缩感知重构算法之子空间追踪（SP）[EB/OL].https：//blog.csdn.net/jbb0523.

（责任编辑：江 艳）