巴丹吉林沙漠潜水蒸发的数值模拟研究

2019-10-14周燕怡王旭升

水文地质工程地质 2019年5期

周燕怡，王旭升

(中国地质大学(北京)水资源与环境学院,北京 100083)

潜水蒸发是指浅层地下水在包气带向上运移、贡献给陆面蒸散的过程，属于地下水的一种排泄方式。潜水蒸发的机理涉及液态水向上运移和表土蒸发2个过程[1]，后者也可以称为土体中的水分蒸发[2]。土体中植被根系吸水产生的蒸腾作用也是陆面蒸散的重要组成部分，属于土壤-植物-大气连续体(SPAC)过程[3-4]。潜水蒸发可以通过水分和盐分的输送影响SPAC过程，因此又被扩展为GSPAC过程[5]。在干旱区，潜水蒸发是地下水排泄的重要方式，它不仅向地表和大气输送水分，而且把地下水循环过程中携带的物质(包括潜在污染物)输送到地表产生环境影响，例如“水走盐留”造成土壤次生盐渍化。潜水蒸发的强度随着地下水位的加深而减弱，其关系可以用简化公式表示，但属于地区经验，取决于具体的条件。一般认为存在一个极限埋深[6]，当地下水位深度超过临界值时，潜水蒸发为零。受地形起伏影响，地下水埋深在很小的空间范围也可能发生较大的变化。因此，大面积区域潜水蒸发的评估需要考虑不同空间尺度的地形变化。Li[7]等以新疆焉耆盆地为例进行分析，发现区域潜水蒸发量的计算结果在一定程度上取决于数字高程的栅格分辨率。地下水盐度[8]和季节性冻结[9]也对潜水蒸发量有影响。

内蒙古西北部的巴丹吉林沙漠属于典型的极端干旱区。与干旱气候形成反差的是，这片沙漠分布大量的湖泊。研究者指出该沙漠湖泊的维持依赖于地下水排泄[10-12]。关于沙漠地下水的来源，很多研究者提出了一些富有争议的推测[13-15]。Dong等[16]将这些推测分类为4种假说。导致地下水来源争议的另一个焦点问题就是地下水的消耗，即巴丹吉林沙漠每年消耗多少地下水。不少研究者根据气象数据计算了沙漠湖泊的蒸发耗水量[16]，但忽略了干旱区常见的潜水蒸发耗水。陈添斐[17]在进行巴丹吉林沙漠湖泊群地下水模拟时，发现无湖洼地的潜水蒸发总量可能与湖面蒸发总量相当。这意味着潜水蒸发在巴丹吉林沙漠具有突出的作用。不过，该模拟结果是使用线性蒸发假设、取极限埋深为1.5 m的情况下得到的，并不一定能够代表沙漠潜水蒸发的真实特征。

为了更加准确地评估巴丹吉林沙漠地下水的消耗量，必须弄清楚潜水蒸发强度与地下水埋深之间的关系。受到环境条件和仪器设备的限制，在巴丹吉林沙漠直接观测不同水位深度的潜水蒸发非常困难。为此，本文以巴丹吉林沙漠的基本气候和砂土环境特征为背景，开展不同地下水埋深条件下的SPAC过程数值模拟，力图提供更加可靠的定量依据用于计算沙漠潜水蒸发量。

1 研究区概况

巴丹吉林沙漠位于内蒙古阿拉善高原，面积约5×104km2，其东南部有高大沙山和湖泊交错分布的奇特景观。沙漠中没有地表河流，因此地下水是湖泊水分的唯一来源。作为干旱区，巴丹吉林沙漠多年平均降水量较少，介于50～150 mm，自东南向西北降水量逐渐减少，一年之中降水主要发生在6—8月。与降水量偏少的特征相反，沙漠周边气象站观测到的水面蒸发量很大，多年平均蒸发量均超过2 500 mm(小型蒸发皿)。在地质构造上，巴丹吉林沙漠属于阿拉善地块，发育断陷沉积盆地，厚度超过500 m的孔隙和裂隙含水层广泛发育[18]。沙漠表层主要被第四系风积沙覆盖，风积砂具有较强分选性，粒径在0.075 ～2 mm范围内的颗粒占80%以上，粉黏粒含量很低，属于细砂[19]，孔隙度0.35～0.42。根据前人研究[20]，风积沙的天然干容重一般为1.48～1.68 g/cm3，内摩擦角在31°～39°，压缩系数小于0.1 MPa-1。

巴丹吉林沙漠植被主要沿着湖泊分布，在地下水埋藏较浅的洼地也有分布。植被在局部地形上的空间变化反映了潜水蒸发与地下水埋深之间的关系。图1以苏木吉林湖区为例，反映了沙丘地下水和植被分布的剖面特征。在靠近湖泊的地带，地下水埋深变浅甚至形成侵蚀下降泉，流动水体减弱了盐碱化问题，有利于形成草地。但是，在苏木吉林北湖的南部，地势平坦，地下水埋藏浅，强烈的潜水蒸发作用导致了盐分的累积，形成盐碱地，仅有喜盐草类稀疏生长。总体上，从湖岸到沙丘高处，植被景观呈现草地—稠密灌丛—稀疏灌丛或裸沙的分带变化，与地下水埋深的分带变化相对应。

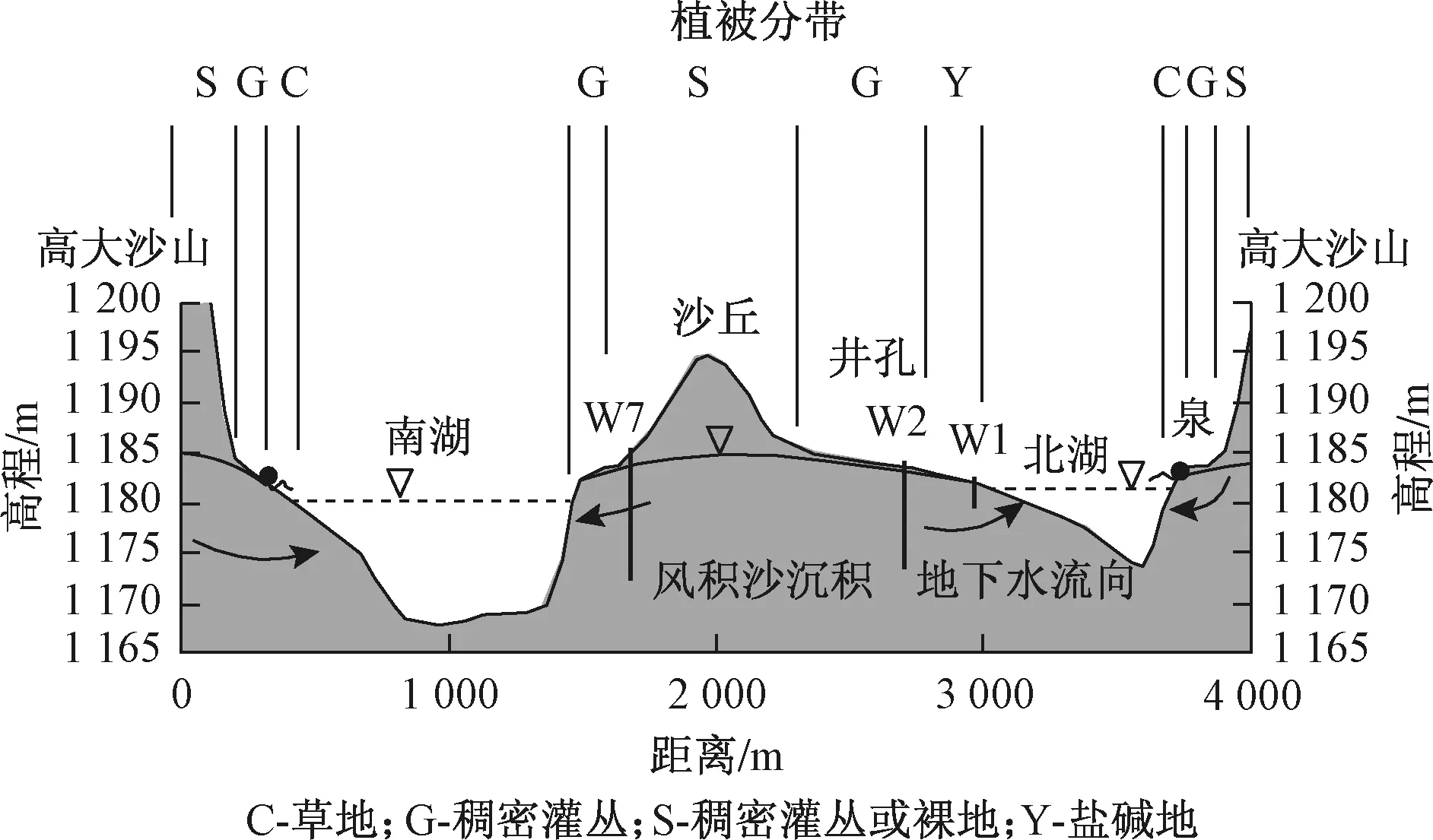
图1 苏木吉林湖区水土环境特征典型剖面图[12]Fig.1 Schematic profile of the soil-water environment across the Sumujilin Lakes[12]

巴丹吉林沙漠潜水蒸发作用反映在土体含水率随深度的变化。笔者在苏木吉林湖区使用土壤水分传感器TDR进行了夏季不同深度含水率的原位观测，结果见图2。图中3个观测场地代表了地下水埋深在0.5～1.5 m之间不同情况。DS-11和DA-1测点的地下水埋深都小于1.0 m，含水率随着深度加大而增加。土壤含水率越低，毛细水吸力越大，在剖面上形成了持续从潜水面吸收水分到地表蒸发的水势梯度。在DW-3测点，地下水埋深接近1.3 m，总体上存在随深度加大含水率增加的趋势。但是在剖面深度1.0 m范围内出现了含水率的2个峰值。第1个峰值大致位于深度0.1 m处，第2个峰值大致位于深度0.4 m处，含水率都低于20%。由于风积砂比较均匀，这种含水率的变化不太可能是土质变化导致的，而是观测之前若干次强降雨入渗形成的，造成了水势剖面上的零通量面，峰值点上部水分向上运移，峰值点下部水分向下运移。这意味着当地下水埋深较大时，潜水蒸发的作用较弱，强降雨形成入渗可以在某个时期内超过蒸发作用导致包气带水分向下运移。这种蒸发和入渗的交叠作用增加了潜水蒸发过程的复杂性。

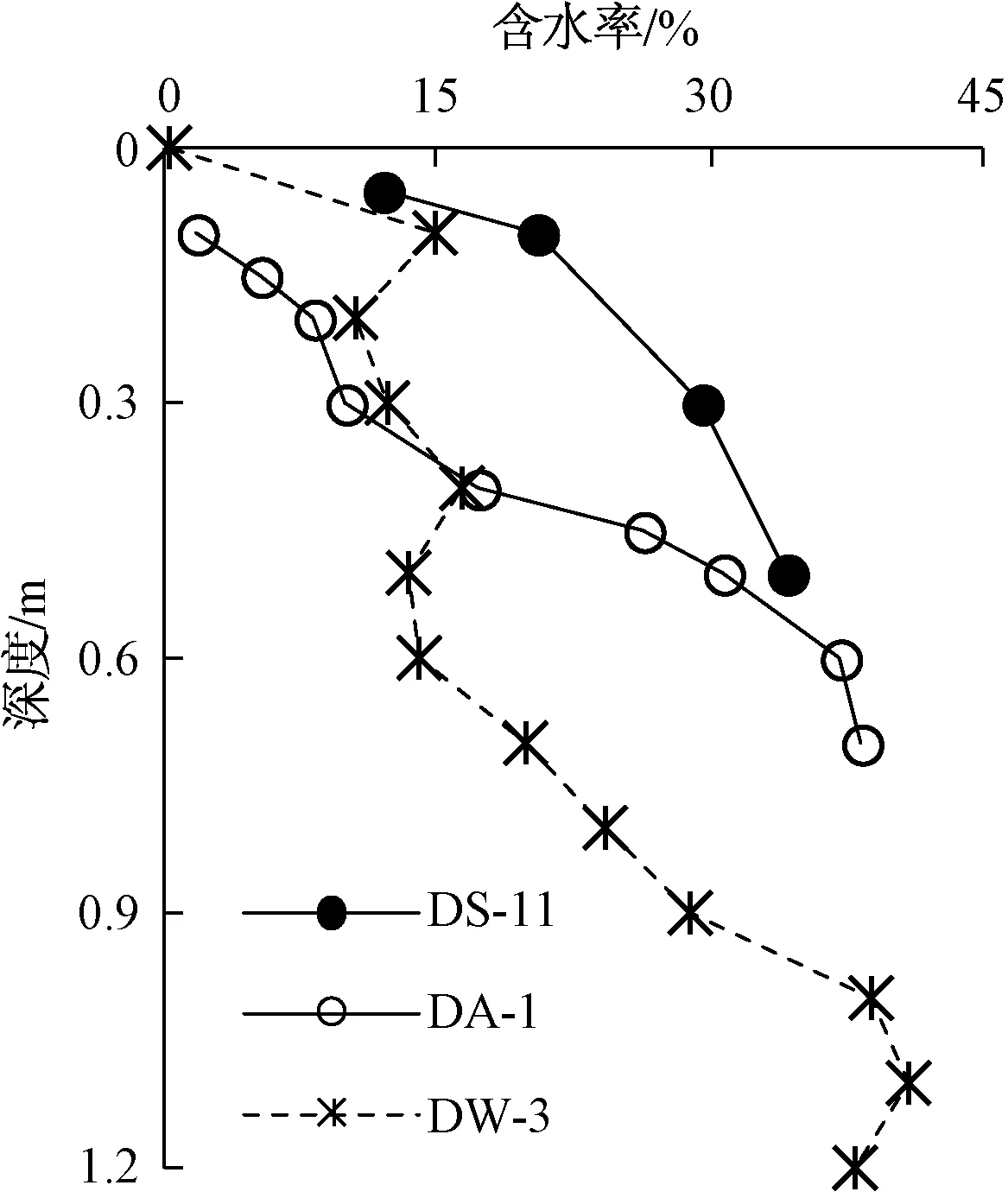
图2 巴丹吉林沙漠地下水浅埋区土壤含水率随深度的变化特征[21]Fig.2 Depth-dependent soil moisture content at typical sites with shallow groundwater in the Badain Jaran Desert[21]

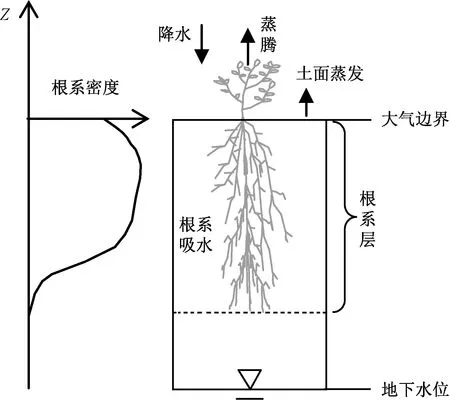
图3 潜水蒸发一维土柱概念模型Fig.3 1-D conceptual model for estimating groundwater evaporation

2 潜水蒸发模型设计

2.1 概念模型和模拟工具

潜水蒸发涉及地下水与SPAC过程的相互作用，需要考虑SPAC的各种要素，包括土壤、植物和大气边界。SPAC过程以垂向水分交换为主。本文建立一个受地下水影响的垂向一维SPAC模型，研究不同地下水位埋深情况下的潜水蒸发问题。模拟工作采用Hydrus-1D软件[22]。

如图3所示，模型的底部为潜水面，处理为定水头边界，上部是一个SPAC系统，以大气边界为驱动条件。SPAC的包气带发生土壤水分的非饱和渗流运动，采用一维形式的Richards方程描述[23]：

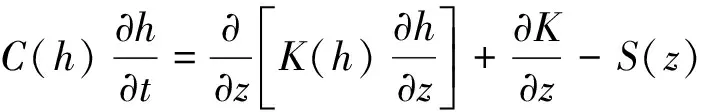
(1)

式中：z——垂向坐标/m, 以向上为正；

t——时间/d；

h——土壤水的压力水头/m；

K(h)——随压力水头变化的渗透系数/(m·d-1)；

C(h)=∂θ/∂h——土壤容水度/m-1，反映的是含水率θ随压力水头变化的特征；

θ——随h的变化采用土水特征曲线表示；

S(z)——随深度变化的单位体积根系吸水强度/(d-1)。

模型的边界条件，地面边界：

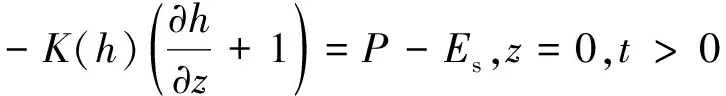
(2)

潜水面边界：

h=0，z=-d，t>0

(3)

式中：P——降水强度/(m·d-1)；

Es——土面蒸发强度/(m·d-1)；

d——地下水位的埋深/m。

非饱和土壤的压力水头为负值，h=0表示潜水面处砂土饱和、压力水头为零。Hydrus-1D模型对蒸散发的模拟有专门的处理方法。首先，蒸散总量被分解为土面蒸发和蒸腾2个部分，并且都与潜在蒸散量成正比[24]：

Ep=ETpe-ηLAI

(4)

Tp=ETp(1-e-ηLAI)

(5)

式中：ETp——潜在蒸散强度/ (m·d-1)，取决于气象条件；

Ep和Tp——土面蒸发和植被蒸腾强度的最大可能值/ (m·d-1)；

LAI——叶面积指数；

η——消光系数(本文按经验取η=0.6)。

在2个潜在蒸散分量中，Ep控制土面蒸发Es的计算，Tp控制根系吸水强度S(z)的计算。其中，Es的计算需要考虑表层干砂的最大吸力，即-hmax。按照Hydrus-1D推荐的做法，本文采用土水特征曲线中含水率为θr+0.005时对应的压力水头确定最大吸力(θr为砂土残余含水率)。在Hydrus-1D中，根系吸水采用随根系密度变化的分配函数和特定的水分胁迫函数计算。本研究采用Hydrus-1D嵌入的S-shaped模型[25]作为根系吸水的水分胁迫函数，该模型包含P0和P50两个参数。P0为衰减指数，取Hydrus-1D建议的经验值(P0=3)。P50指根系吸水强度衰减到50%对应的压力水头，取经验值(P50=-1 m)。在根系层，根系密度也是随深度变化的(图3)，与具体的植被景观特征有关。本文将在植被情景设计中对此加以处理。模型上边界的驱动条件采用重复年周期波动的逐日降水量和潜在蒸散量数据，因为本文主要研究某些气候情景下的多年平均周期性行为(取周期长度为365 d)。模型初始条件假设为压力水头与潜水面形成静水力学平衡状态，在反复周期模拟中，初始条件的影响将逐步消失，达到重复性的周期变化状态。

本文模型在垂向上采用均匀的剖分方式，离散节点的间距为10 cm。测试结果表明更高的模型分辨率并不会显著改善模拟结果的精度，因此10 cm的节点间距对本文研究是可行的。在时间剖分上，根据数值计算的收敛特征，采用Hydrus-1D的变步长迭代法，最小时间步长为0.000 01 d，最大时间步长为5 d。模型含水率迭代精度取0.001。每一种气候情景下的模拟时间为20年，取最后1年的结果代表多年平均周期状态。对比观察不同时期的模拟结果，表明模拟时间达到10年以上则初始状态不确定性导致的年际变化均小于5%，因此取第20年的结果足以消除初始条件的影响。

取得多年平均状态周期解的逐日模拟数据后，计算多年平均潜水蒸发量：

(6)

式中：Eg——多年平均潜水蒸发量/mm；

i——一个周期年内的天数；

Vi——潜水面处即模型底部的逐日水分通量/(mm·d-1)，向上为正；

δ——阶跃函数，即Vi>0时δ=1，否则δ=0；

Δti——累加时间步长，取Δti=1 d。

使用阶跃函数的目标，是单纯提取出潜水面对蒸散发的贡献，而筛除掉降水入渗对地下水的补给。

2.2 气候情景

巴丹吉林沙漠的周边分布有多个气象站，具备长期气象观测数据，而沙漠内部只在近几年才开始气象观测。根据周边气象资料，巴丹吉林沙漠降水量具有东南高、西北低的特点，多年平均降水量为40～150 mm。小型蒸发皿(E20型)水面蒸发量与降水量分布趋势相反，东南部为3 000～3 500 mm/a，北部可达4 000 mm以上。2012年，中国地质大学(北京)在沙漠腹地的苏木吉林南湖架设自动气象站[12]，对降水量和湖面蒸发量(E601型蒸发皿)进行观测。该自动气象站的数据能更准确地反映沙漠湖泊区气象条件，作为本次模拟研究的基础数据，其中2013年完整年的逐日降水量和蒸发量数据见图4。该年的总降水量约为157.4 mm，总蒸发量约为1 314 mm。本文取该气象站E601型蒸发皿观测的水面蒸发量为潜在蒸散量(ETp)，替代其它气象数据计算潜在蒸散量的简化方法。

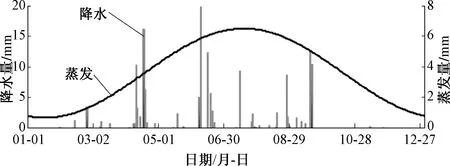
图4 苏木吉林湖区2013年气象要素逐日变化特征Fig.4 Daily meteorological data in the Sumujilin lake area in 2013

为了反映沙漠气候环境的时空变化，在设计模型的气候情景时，取参考年的降水量代表沙漠相对湿润气候情景(用符号C1表示)。通过去除一些雨强较小的降雨事件，使总降水量降低到100 mm，作为沙漠的平均气候情景(用符号C2表示)。进一步去除更多雨强较小的降雨事件，使总降水量降低到50 mm，作为沙漠相对干燥气候情景(用符号C3表示)。潜在蒸散量如何随干湿环境变化是一个比较复杂的问题，目前缺少定论。为便于对比不同地下水埋深对潜水蒸发的影响，本文假设潜在蒸散量在各个气候情景中保持不变。

2.3 砂土参数

砂土的非饱和土水特征曲线一般用相对饱和度Se作为参考：

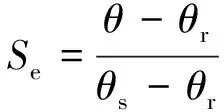
(7)

式中：θr和θs——残余含水率与饱和含水率。

在Hydrus-1D中，推荐使用V-G公式[26]表示土壤含水率与压力水头之间的关系，并以此计算不同相对饱和度下的渗透系数，即：

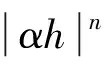
(8)

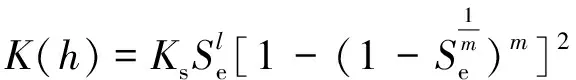
(9)

式中：α——与土壤进气值有关的参数/m-1；

n——无量纲的参数，m=1-(1/n)；

Ks——饱和渗透系数/(m·d-1)；

l——孔隙弯曲度的参数，依据经验可取为0.5。

实际的土水特征曲线还需要考虑吸湿和脱湿过程的滞后效应，对短期行为和微观机理研究比较重要。本文主要研究长周期行为，这种滞后效应暂不予以考虑。

对于巴丹吉林沙漠，已经通过采样法进行了砂土水分特征曲线的研究[19, 21, 27-29]，包括压力膜仪法和离心机法测试水分特征曲线获取的VG公式拟合参数(θr、θs、α、n)。这些参数都有一定的变异性，其中θs的变异性最小。此外，采用单环入渗仪在沙丘表层进行了饱和渗透系数的观测[30]，发现风积砂的Ks为0.5～75 m/d，有一个较大的变化范围。实际上，巴丹吉林沙漠的第四系沉积物有一定的空间变异性，普遍为细砂，局部地区也存在中砂、粗砂沉积。关于砂土参数的变异性，前人进行了一些定量研究[31-32]。通过收集大量土壤样品(包括砂、黏土、壤土以及粉土)数据，Carsel和Parrish[32]建立了θr、Ks、α和n等参数的耦合随机模型，其中含有砂土的概率统计参数，与巴丹吉林沙漠的砂土特征具有相似性。笔者参考该方法对砂土参数进行Monte Carlo模拟，得到5 000个砂土参数的随机组并分析了包气带水下渗的不确定性[33]。本文以研究地下水埋深的影响为重点，在砂土参数变异性方面做了简化处理，即设计出3个砂土参数组合分别代表细砂、中砂和粗砂的情景。各种情景下的V-G公式参数见表1。由于不同砂土类型的θs变异性并不大，在此统一取最大值0.42。

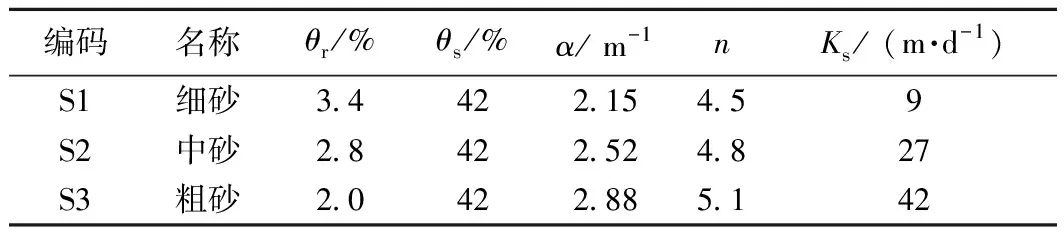
表1 砂土特征参数的三种组合情景

2.4 地下水埋深和植被情景

在巴丹吉林沙漠干旱区，植被覆盖特征对地下水埋深具有高度依赖性(图1)，在模型中的具体表现之一就是叶面积指数的季节性变化特征随地下水埋深而变化。杜占池[34]等对内蒙古典型草原地区沙地植物的叶面积指数(LAI)进行了研究，发现LAI最大值通常出现于8月份。唐思凌[35]等对典型沙生灌木的研究表明沙蒿生长季为4月底到10月下旬，4月底—7月初LAI为稳步上升，达到最大值的10%～90%，7月初到9月中旬为稳定期LAI接近最大值，9月中旬到10月下旬LAI迅速降低。本文参考这些研究结果，在潜水蒸发模型中将植被生长季确定为5—10月，各月LAI按照固定的比例周期变化，分别为最大LAI的30%、70%、100%、100%、75%、50%，非生长季的LAI取为零。考虑到随着地下水埋深的加大，植被总体上向稀疏和无覆盖状态转变，模型的最大LAI随水位埋深情景(0.2～3.0 m)的不同而在2.5～0.1之间变化(表2)。

植被根系吸水与地下水埋深有关。有研究者对沙漠草地根系特征进行研究[36-37]，表明沙地草本植物的根系主要分布在深度0.5 m以内，蒿类的根系可以达到1.0 m，根系密度均匀分布或随深度线性减小，浅根一般均匀分布。前人对油蒿和柠条的研究[38]表明沙漠灌木最大根系深度可达1.5～3.0 m，最大根系密度一般出现在0.3～0.5 m，以下根系密度随深度增加近似指数衰减。结合已有研究，本文假设植被根系密度在地下水埋深0.2 m时为均匀分布，在地下水埋深为0.5～1.0 m时随深度线性减小，在地下水埋深1.5～3.0 m时随深度呈中部大两头小的方式变化。同时，按照Hydrus-1D的要求，确保根系密度函数在整个根系层的积分为1。模型中不同深度段的根系密度见表2。

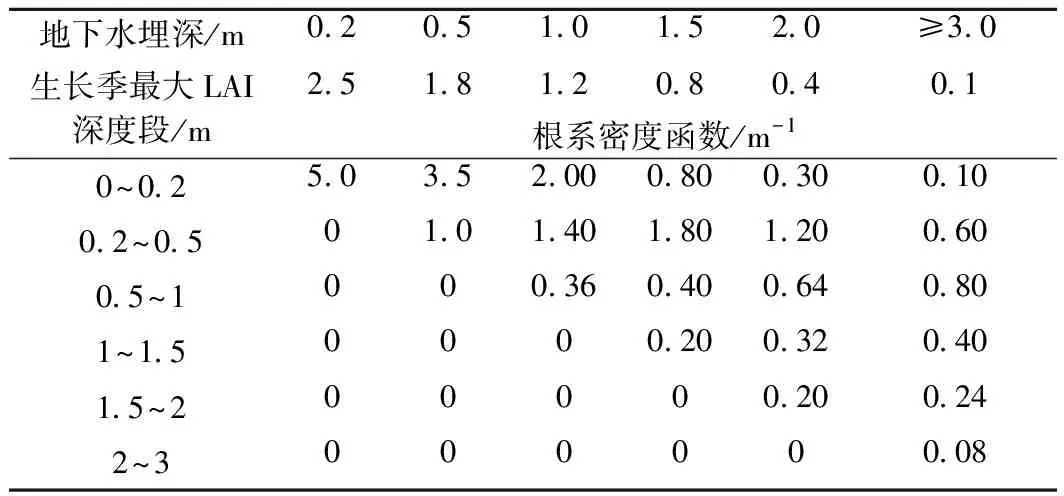
表2 不同模拟情景的地下水埋深和植被特征

本文假设根系的深度和密度函数并不随季节变化，只有LAI随季节变化，代表特定气候背景下植被种群稳定分布的状态。另外，本文暂不考虑盐分运移对潜水蒸发和植被的影响。地下水埋深浅(d<0.5 m)时可能发育植被稀疏的盐碱地，但这时的总蒸散量不管有无植被都很强，不会显著影响对潜水蒸发的计算结果。

本次研究包括3种气候情景(C1, C2, C3)，3种砂土参数情景(S1, S2, S3)和6种地下水埋深(最大埋深为3.0 m)情景，一共设计有54个情景模型。实际上，为了寻找潜水蒸发的极限埋深，对地下水埋深大于3.0 m的情况也进行了模拟，即试探性的将模型深度调整为3.1 m、3.2 m、……, 直到在年周期的任何时刻都不存在潜水蒸发为止。

3 模拟结果分析

3.1 潜水蒸发强度的季节性变化特征

Hydrus-1D能够计算逐日的模型底部水分通量，根据这些数据可以观察潜水蒸发强度的季节性变化。图6给出了平均气候情景(C2)和细砂(S1)情景下的模型底部水分通量V(式6)的变化曲线，包括地下水埋深为1 m和2 m两种情况的模拟结果。当V>0时，模型底部水分向上运移，说明发生了潜水蒸发；当V<0时，则水分向下运移，包气带水下渗补给地下水。从图6可以看出，当地下水埋深为1 m时，多数时间V>0，即以潜水面蒸发为主，只有少数发生降水的日期及雨后的若干天内出现V<0的情况，而且呈现一种显著的锯齿状变化。这说明当地下水埋深比较浅的时候，强降水比较容易转化为地下水补给。对于V>0时，d=1 m情景的潜水蒸发强度存在显著的季节性振荡，在7月份达到峰值，与潜在蒸散量(图4)的变化趋势基本一致。相比之下，地下水埋深为2 m的情景显示出非常平缓的V值变化，似乎只有3次降水事件引发了潜水面处的下渗补给，但是每次V<0持续的时间比d=1 m的情景更长一些，而开始出现V>0的时刻均落后于强降雨发生时刻。这实际上反映了包气带对降水-入渗补给过程的滞后延迟作用，包气带厚度越大，滞后效应越显著。不过，仅观察逐日变化曲线难以判断地下水的年补给量如何随潜水面深度而变化。虽然d=1 m时，响应降雨事件的V绝对值要大于d=2 m的情景，似乎意味着地下水获得了更多的补给，但其潜水蒸发的强度远大于d=2 m的情景，说明消耗的地下水也很多。只有通过累计年蒸发量与年降雨量比较才能最终判断实际地下水补给量与消耗量之间的关系。

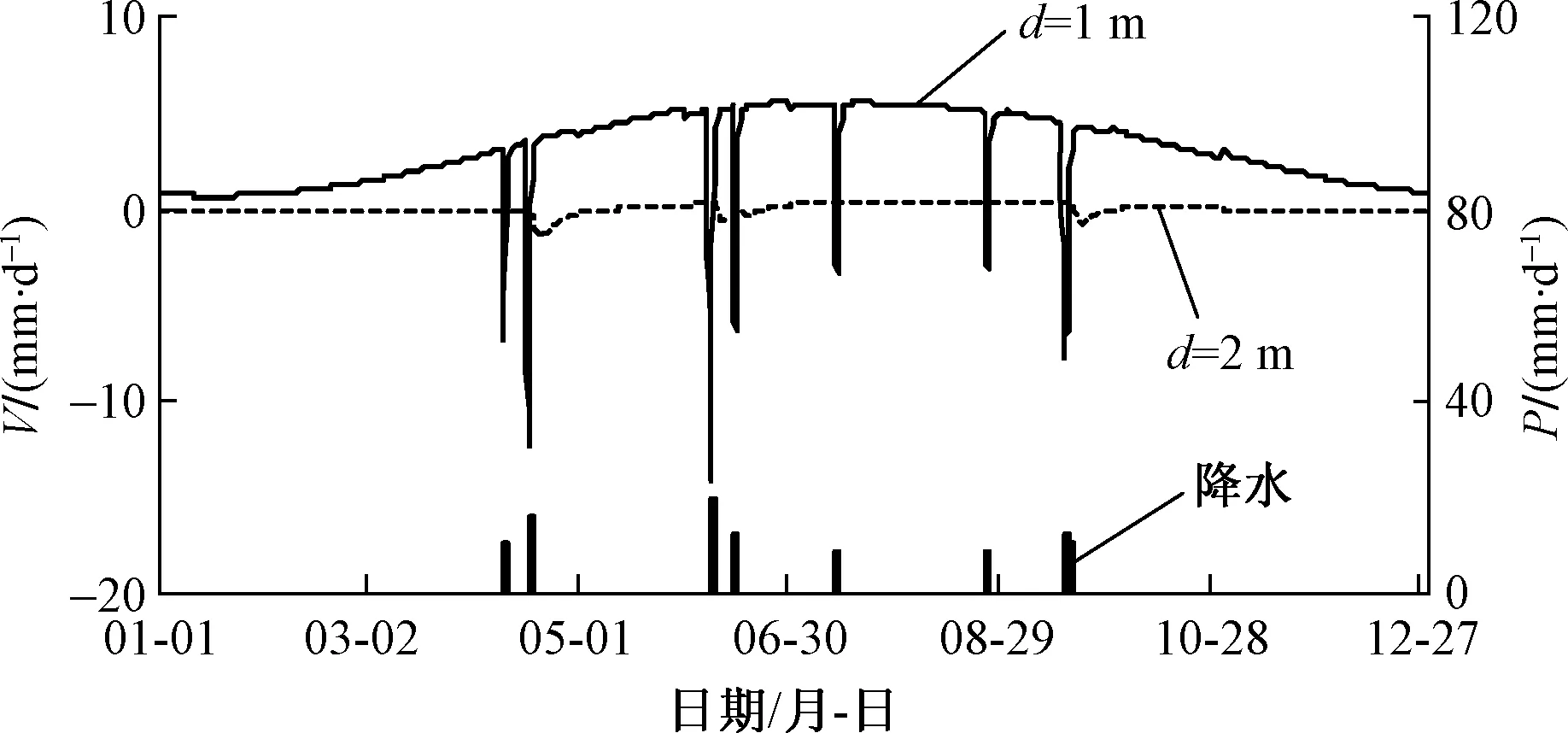
图5 平均气候(C2)和细砂(S1)情景下底部水分通量(V)以及降水(P)的逐日变化(d表示地下水埋深)Fig.5 Daily variation patterns of the bottom flux (V) in the model and the precipitation (P) for the scenarios of average climate conditions (C2) and fine sands (S1), where d is the depth to water table

3.2 多年平均潜水蒸发量与地下水埋深的关系

为了在年尺度上观察地下水与SPAC系统的水量交换，需要把逐日水分通量的模拟结果在周期年内进行累计，例如多年平均潜水蒸发量按照式(6)进行计算。采用类似的累计方法可以计算出多年平均的土面蒸发量(Es)和蒸腾量(Ta)，实际蒸散量为两者之和，即ETa=Es+Ta。将地下水的净补给计算为：

Rg=P-ETa

(10)

其中，Rg代表多年平均状态下的地下水净补给，即超过年蒸散量的部分年降水量转化为地下水补给。如果Rg<0，意味着降水量不足以支撑蒸散量，必须通过潜水蒸发补充。图6针对9种典型情景，给出了关键水分通量年累计值随地下水埋深的变化特征。总体看，当潜水面深度小于2 m时，这些水分通量对地下水埋深的变化都比较敏感，而且不同情景的数据显示出一定的差异；潜水面深度超过2 m时，水分通量趋于稳定，随地下水埋深的变化只有少量的调整。

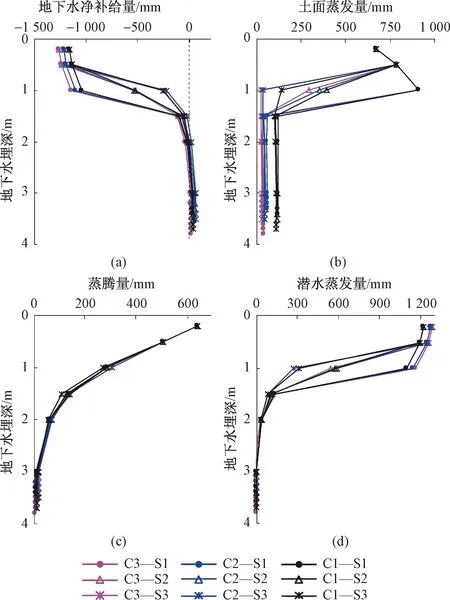
图6 模型水分通量要素多年平均值随地下水埋深的变化Fig.6 Variations in the mean annual values of the simulated water flux components

由图6(a)可知地下水净补给量(Rg)可正可负，当d<2时，总是有Rg<0，表明蒸散消耗的水量总是大于降水量，需要潜水蒸发进行补充。在相同的砂土参数情景和地下水埋深情况下，气候越干旱(从C1到C3)，Rg越小，即潜水蒸发的贡献越大。相比之下，砂土类型变化引起的差异较小。当地下水埋深较大时，可以获得真正的入渗补给(Rg>0)，但在最好的情景下年补给量也不超过40 mm，说明沙漠的地下水补给受到很大的限制。

土面蒸发量随地下水埋深的变化不仅具有非线性特征，而且在d为0.5～1.0 m的区间会出现峰值(图6b)，变化曲线整体上呈反S型。这种特征是2个相反的趋势叠加造成的。首先，随着地下水埋深变浅，表土变湿润，蒸发强度向最大可能土面蒸发量Ep靠拢。其次，地下水埋深变浅导致LAI增大产生强烈的遮光效应，按照式(4)分配的Ep值变小。这2个相反变化趋势的叠加产生了Es的峰值。然而，这种叠加效应对蒸腾量的变化曲线(图6c)几乎没有影响，而且不管情景如何，蒸腾量的变化都近似为同一条曲线，似乎说明根系吸水的自我调节作用使得实际蒸腾量只随最大叶面积指数变化。不过，需要意识到本文模型没有考虑发生盐碱化的情况，因此当d<0.5 m时，单独的土面蒸发量或蒸腾量模拟结果都不能代表实际可能发生的情况，只有两者的总和(即ETa)才有意义。

多年平均潜水蒸发量(Eg)随地下水埋深的变化显示在图6(d)中，可以看出Eg随地下水埋深增大而减小的趋势具有显著的非线性特征，并且存在使得Eg=0的极限埋深。总体而言，各种情景下的极限埋深都大于3 m，而且在d=3 m时潜水蒸发量都小于最大值的5%。当d在0.5～1.5 m区间，Eg对地下水埋深的变化十分敏感，反映了砂土毛细水平均上升高度一般小于1.0 m的特征。当d=1.0 m时，Eg对砂土类型的变化也非常敏感，细砂(S1)的潜水蒸发量远远大于粗砂(S2)的情景，相比之下，干湿气候情景变化对潜水蒸发量的影响是微弱的。然而，在d<0.5 m和d>1.5 m的区间，潜水蒸发量对地下水埋深、气候情景和砂土类型的变化都不太敏感。

3.3 经验公式和极限埋深

图6(d)潜水蒸发量随地下水埋深的变化曲线近似呈S型，与土壤含水率随压力水头的关系曲线有较高的相似度。笔者试图采用线性、抛物线型或指数型的经验公式对曲线进行拟合，效果都不理想，会产生很大的误差。考虑到V-G公式成功地刻画了S型土水特征曲线，本文提出采用一个类似V-G公式的关系式拟合潜水蒸发曲线：

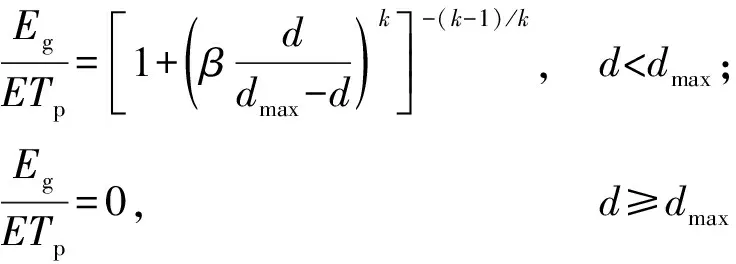
(11)

其中，β和k都是无量纲参数，且k>1。dmax为极限埋深，极限埋深的数值根据模拟结果直接确定，因此对于每种情景只需要优化出β和k两个参数的取值即可。式(11)可以很好地拟合各种情况下的潜水蒸发曲线，误差均小于0.1，而且可以比较准确地反映在d/dmax处于0.2～0.4区间时曲线的急剧变化特征。有关参数见表3，典型的拟合曲线特征见图7。

表3 不同情景下潜水蒸发特征经验式(11)的参数

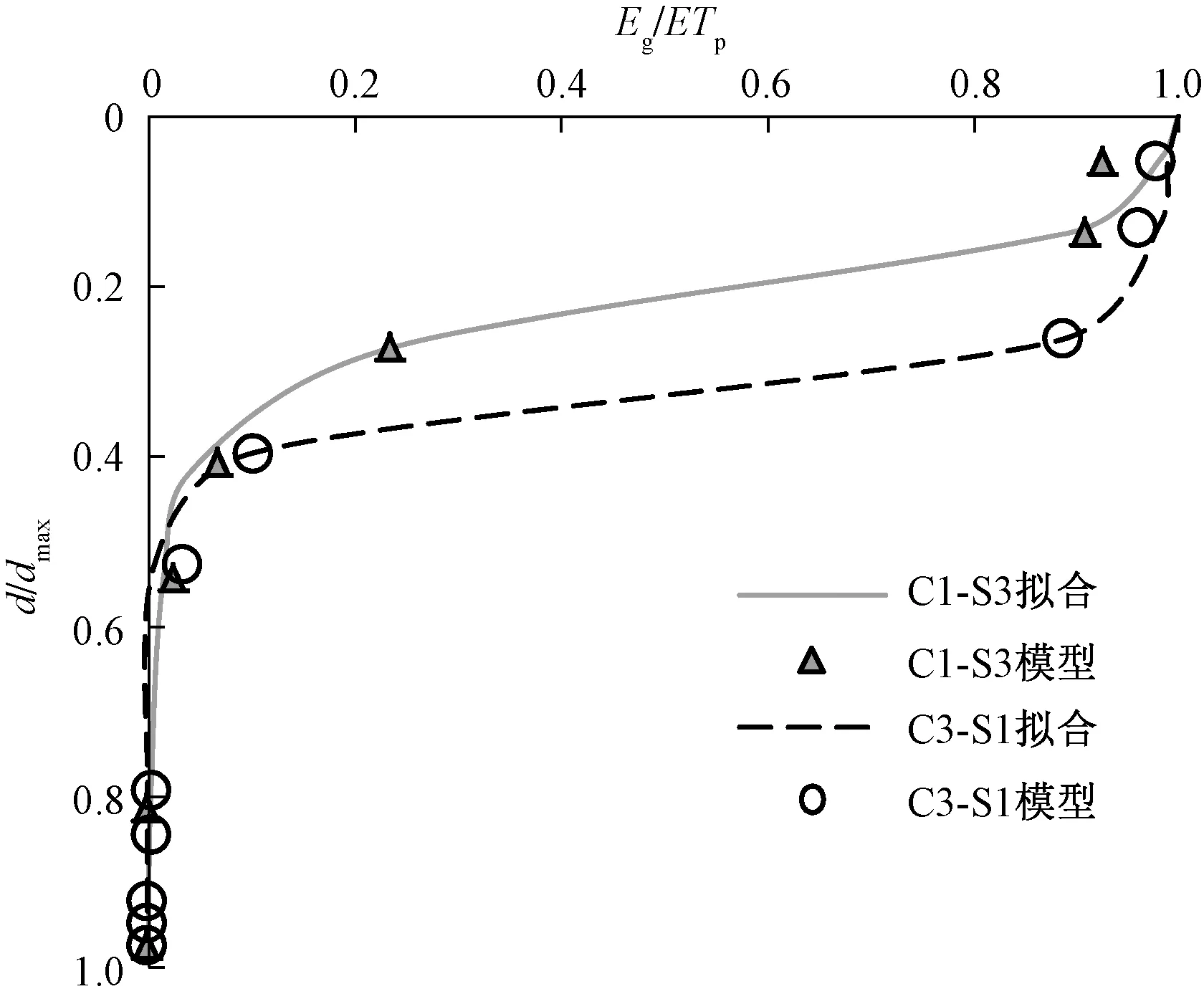
图7 式(11)拟合潜水蒸发曲线的效果对比图Fig.7 Comparison between the fitting curves by using Equation (11) and the modeling data points

从表3可以看出，不同情景的极限埋深在3.3～3.8 m变化，平均值接近于3.5 m，极限埋深总体上随着土质变粗(从S1到S3)和气候情景向干燥方向迁移均不是单调的增减变化，其机理尚不清楚。参数β的变化比较有规律，即随着砂土颗粒变粗，其数值增大，这与表1中α参数的变化特征类似。气候情景对参数β的影响相对较小。参数k为4.8～10.7，总体上随着气候情景向干旱化方向发展而增大，但随着砂土颗粒变粗并不显示出单调的增减变化，似乎在中砂的情景中其数值最小。

4 成果应用与讨论

本文模拟研究得到的结果集中体现在式(11)和表3中，可以用于对巴丹吉林沙漠的潜水蒸发量进行重新评估。为了便于对比，本文计算潜水蒸发量的空间范围与陈添斐[17]所取的范围相同，属于30 km×23.6 km的矩形区域。该区域发育了15个大小不同的湖泊，湖泊总面积约为8.9 km2。根据已知的200 m分辨率数字高程数据和地下水位栅格数据，可以计算得到地下水埋深的栅格数据。然后，考虑不同的情景，采用式(11)计算每个非湖泊栅格的多年平均潜水蒸发量，累加得到评价区的潜水蒸发总量，与湖面蒸发量进行对比。

在干旱气候(C3)和细砂(S1)情景下，计算得到评价区的潜水蒸发总量为2.9×107m3/a，湖面蒸发总量为1.1×107m3/a。这意味着评价区的潜水蒸发量比湖面蒸发量大1.6倍，二者比值接近2.6∶1。在湿润气候(C1)和粗砂(S3)情景下，潜水蒸发总量为2.6×107m3/a，与湖面蒸发量的比值接近2.5∶1。另外，地下水位动态观测结果显示巴丹吉林沙漠地下水的水位非常稳定[39-40]，年动态变幅小于0.3 m，波动轻微。在平均水位的基础上增加0.15 m或减小0.15 m计算得到的潜水蒸发量，与采用水位平均值得到结果相比，相对偏移量均小于3%。总之，评价区的潜水蒸发耗水显著大于湖面蒸发耗水。

陈添斐[17]模拟计算发现潜水蒸发总量与湖面蒸发总量的比值接近1∶1，这是极限埋深取1.5 m且进行线性插值得到的结果。从图6d可以看出，这样会低估相同埋深下的Eg值，从而造成计算结果偏小。考虑到实际极限埋深大于3.0 m以及Eg呈现的非线性变化，本文计算的结果更加可靠。巴丹吉林沙漠有100多个湖泊，总面积接近20 km2，湖面蒸发总量接近2.3×107m3/a。若按照本文的比例进行估计，则巴丹吉林沙漠无湖洼地的潜水蒸发总量至少达到5.8×107m3/a，两者总和确定的地下水排泄消耗量至少为8.1×107m3/a。以往对巴丹吉林沙漠水均衡的研究容易忽略潜水蒸发，从水均衡分析上来讲显然是不妥当的，需要重新加以考虑。

本文就一些简单情景下的潜水蒸发进行了数值模拟，仅取得了一些初步结论，还存在着许多问题有待进一步研究。首先，目前还缺乏用来校验模型的实测潜水蒸发数据。建议下一步工作中对巴丹吉林沙漠的潜水蒸发进行长期监测，确定各种典型情景下的实际潜水蒸发情况，为进一步校准和完善潜水蒸发模型提供定量依据。其次，本模型只考虑了液态水的运移，实际上，在沙漠包气带，汽流和温度对水分运移的作用也很重要[41-42]。特别是在冻结期，温度对土壤水的运动起主导作用[43]。因此，在下一步的研究中，需要进一步考虑水、汽、热耦合迁移以及冻结期的潜水蒸发问题。第三，本文模型中采用了给定地下水埋深的方式进行模拟，实际上地下水位与蒸发存在相互作用并可能造成地下水位的变动，从而对模拟结果产生影响[44]。为了精确地模拟潜水蒸发量，在下一步的研究中还需要考虑潜水蒸发与地下水位的耦合效应。此外，在沙漠中，湖泊和洼地并非均匀分布。因此，本次研究获得的潜水蒸发量和湖面蒸发量的比值在空间范围上具有局限性，只能对应于本文所选取的计算范围。若是将计算范围扩大到沙漠西北部湖泊较少的区域，可能该比值会更大，这有待于在未来的工作中加以探讨。