基于能量耗散机制的粗粒土圆度损伤特性分析

2019-10-14魏玉峰潘远阳

水文地质工程地质 2019年5期

何亮，魏玉峰，潘远阳，雷壮

(地质灾害防治与地质环境保护国家重点实验室(成都理工大学)，四川成都 610059)

圆度用于反映颗粒原始棱角被磨圆的程度，是颗粒的重要结构特征[1]，探究粗粒土的圆度损伤，对研究粗粒土力学特性具有重要意义。Wentworth C K[2]首次给出了圆度的定义，指出圆度是最尖的角边曲率半径与最长对径一半的比值。 Cherif Taiba A 等[3]运用三轴试验对砂土的颗粒形状进行研究，建立了粉砂颗粒圆度与强度间联系，认为粗粒土的抗剪性能很大程度上依赖于颗粒圆度。Ghalehjough Babak Karimi 等[4]提出基于直剪试验下，颗粒圆度对土的极限承载力影响大，随颗粒圆度增大极限承载力降低。Arun P Raj等[5]通过研究常用的圆度测量仪，建立圆度定量模型，分析了圆度测量的影响因素与试验误差。Vepraskas M J等[6]建立回归模型以确定砂粒圆度和球形度与土壤锥度指数及堆积密度和密集土壤休止角的关系。Zheng J等[7]详细介绍了识别粒子角和拟合圆的算法，用以计算土壤圆度。Zheng Junxing等[8]提出运用计算方法对土壤圆度进行计算，证明了不同类型土壤圆度采用几何计算法优于图表法,分析了计算方法与传统方法分别计算颗粒圆度的差异。基于能量耗散角度研究剪切试验过程中粗粒土圆度损伤特性，能从本质上揭示圆度损伤机制。谢和平等[9]认为岩石变形破坏是能量耗散等综合作用的结果，从能量角度提出了岩石强度准则和破坏准则。李子运等[10]对不同围压下的页岩进行分析，提出了峰前以能量积聚为主，破坏过程发生能量释放和能量耗散，峰后残余强度下重新开始积聚能量，但能量积聚能力和效率不如峰前。岩石变形破坏的过程是和外界产生能量交换的过程，基于理论角度分析岩石破坏的能量传递与耗散，分析岩石损伤扩展过程，对揭示岩石变形破坏本质具有重要意义[11-13]。陈中一等[14]运用MATLAB对花岗岩裂隙萌生扩展的过程研究，探讨了裂隙萌生扩展影响因素并提出研究新思路。Saurer E[15]基于MATLAB分析模型的断裂力学能量平衡和极限平衡方法，定性和定量地模拟非平面剪切带传播速率，剪切过程中具有明显的能量演化特征。

传统的颗粒圆度研究，多集中于颗粒形状的研究[16-17]，未定量从能量角度对其损伤本质进行分析。对于基于能量耗散机制下，建立粗粒土剪切过程圆度损伤模型，分析了粗粒土剪切过程圆度损伤因子变化与圆度损伤能量的定量关联，对探究粗粒土剪切过程圆度损伤的本质是一种有意义的尝试。近年来对粗粒土的相关技术研究成果广泛运用于工程实践中[18]，基于能量耗散机制下对粗粒土圆度损伤进行分析，可从本质上探究剪切过程中的土体状态变化，定性及定量描述圆度损伤的发挥过程，对分析剪切过程中粗颗粒裂纹扩展成因、圆度损伤演化过程具有一定的理论指导意义和工程实用价值。

1 剪切中粗粒土能量的传递与耗散

粗粒土剪切过程中能量不能凭空产生，也不能凭空消失，只能以一种形式转换成另一种形式[19-20]。针对剪切系统粗粒土在法向应力荷载作用下，剪切过程中满足系统能量守恒定律[21]。在外力作用下通过复杂的功能转换关系，基于热力学第二定律[19]，土体作为开放系统，为不可逆过程，致使整个阶段能量逐渐减少。

粗粒土在剪切系统中，以剪切盒粗粒土为整体研究对象，在外力做功初始总能量为E，剪切系统剪切达到应力峰值临界状态具有一个动能增量Ek，以剪切系统作为介质，能量传递至颗粒系统。一部分能量克服摩擦力做功，以摩擦热E0形式散失，基于热力学第二定律知摩擦生热为不可逆过程，致使系统整体能量逐渐减少；一部分转换为颗粒剪胀(剪缩)所需能量E1，宏观体现在颗粒孔隙率增大(减小)；一部分转换为颗粒间重新排列所需能量E2，具体表现为粗粒土在剪切盒内以错动、翻滚、掉落等形式产生动能与势能，另一部分因产生颗粒破碎粗粒土系统吸收部分能量E3。基于系统能量守恒下，可知满足基本理论准则：

E=E0+E1+E2+E3+EK

(1)

式(1)为剪切初始-应力峰值过程中，以粗粒土整体作为研究对象，基于系统能量守恒下建立的能量转化关系，如图1所示。

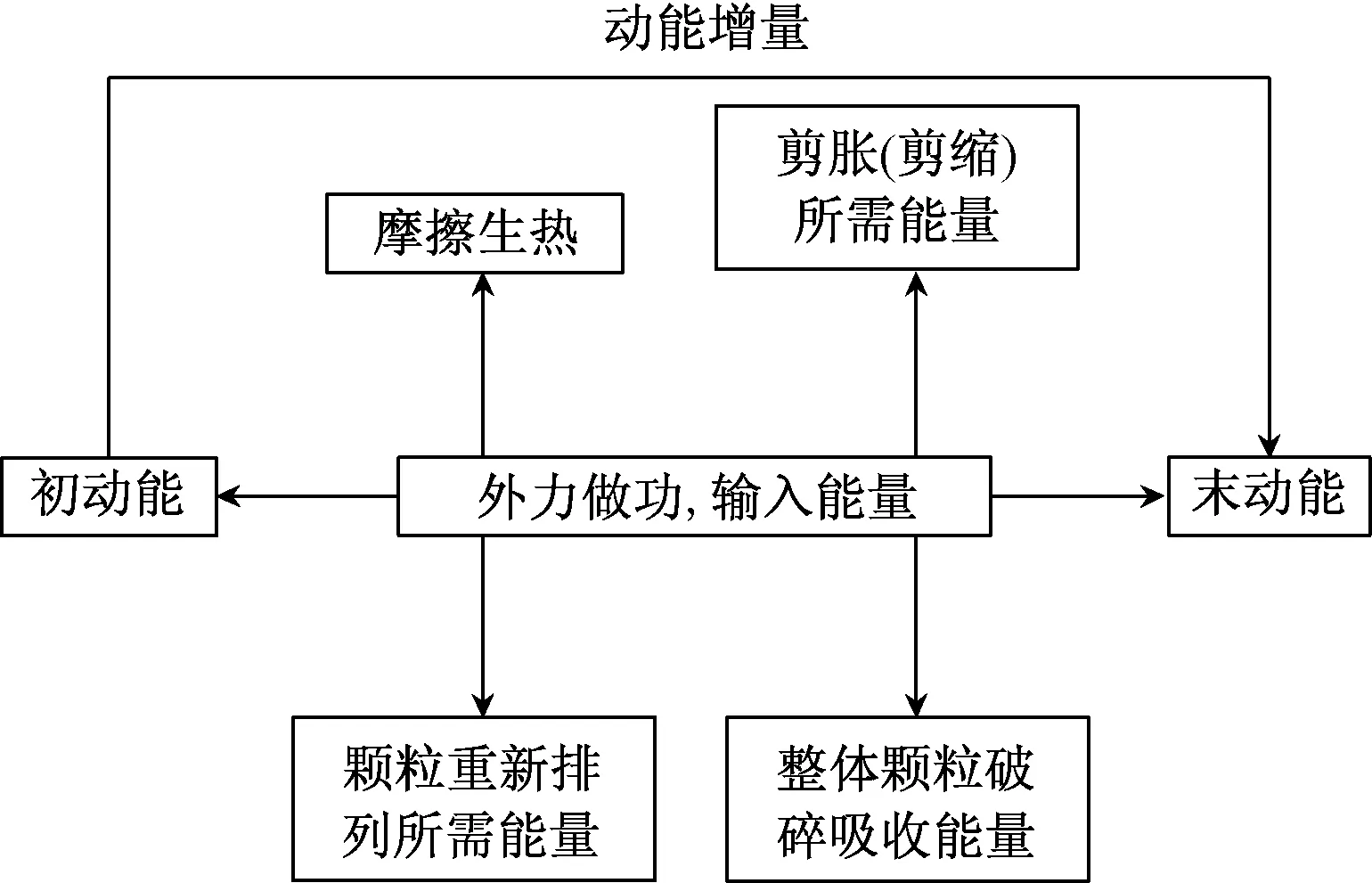
图1 粗粒土系统剪切过程能量转换传递关系Fig.1 Various energy transfer relationships in the shear process of coarse-grained soil systems

剪切过程中，以单个颗粒为研究对象，外力所做功，首先以剪切盒为介质传递到颗粒整体，颗粒粒间应力发生改变，表现出各向异性，以单个颗粒为介质能量发生传递与耗散。一部分能量作为颗粒损伤演化所需能量，颗粒开始产生微裂纹和颗粒产生应力集中，微裂纹在整个过程逐渐增加、汇聚、扩展，逐渐贯通，形成新的微表面；另一部分能量以弹性势能的形式存储在颗粒内部，逐渐积累，弹性势能逐渐汇聚过程中，达到临界状态，以剧烈的方式将能量输出，颗粒产生变形破坏，以动能、摩擦热、声波能、辐射能等形式体现，弹性势能为颗粒变形破坏的主要能量(图2)。

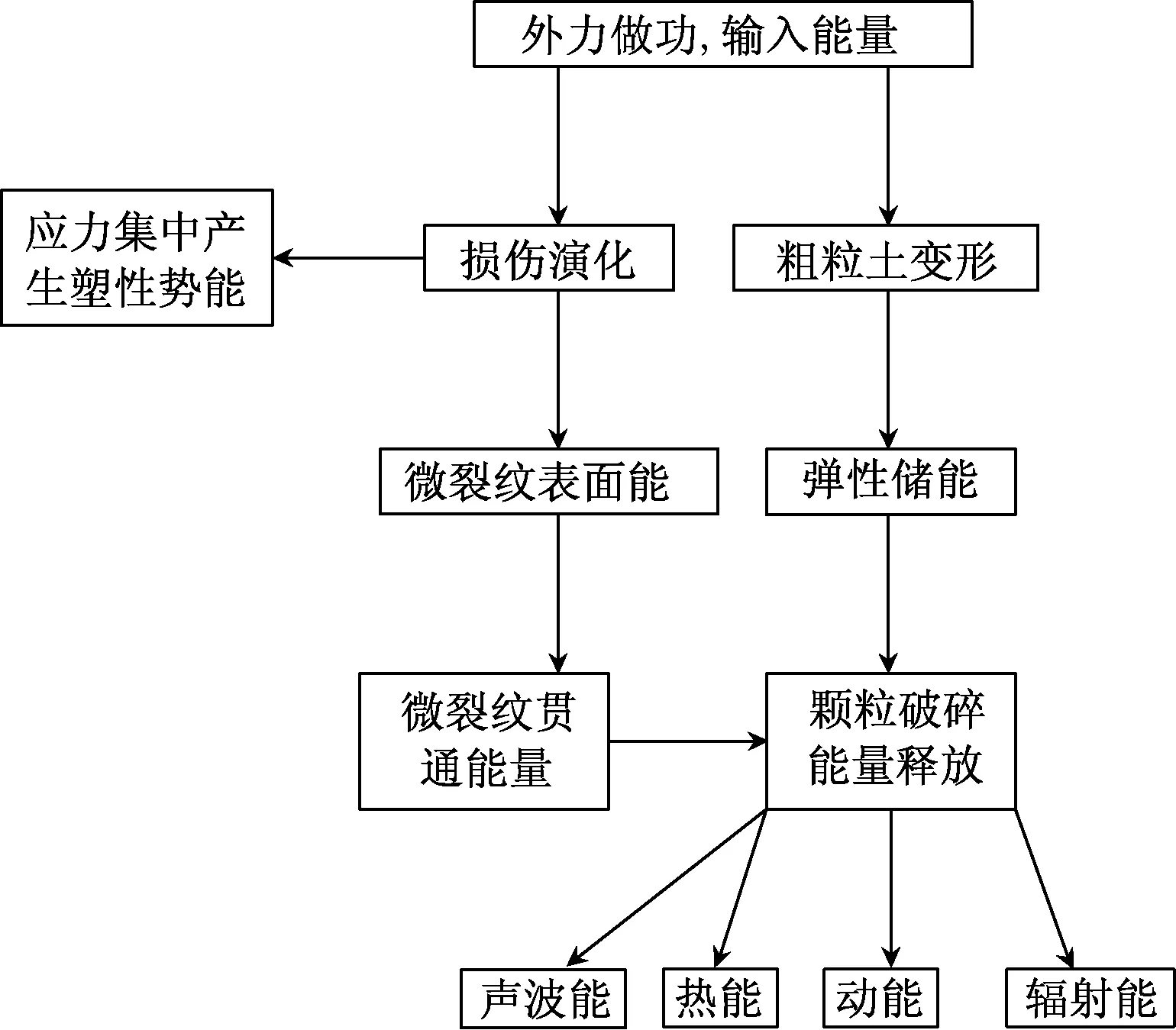
图2 粗颗粒剪切过程能量转换传递关系Fig.2 Energy transfer relationship in coarse particle shearing process

外力做功输入总能量U0，一部分以弹性势能形式储存在颗粒内部(用Ue表示)，另一部分发生应力集中产生塑性势能(Um)。

U0=Ue+Um

(2)

在应力空间下，总能量U0可按式(3)计算：

(3)

弹性势能可按式(4)进行计算：

(4)

式中：Ue——单个颗粒弹性势能；

σi=1，2，3——应力；

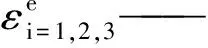
塑性势能虽对于单个颗粒，其所占比例较小，却是产生塑性区域、引起颗粒圆度损伤的关键势能，不可忽略，按式(5)计算：

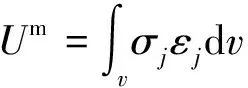
(5)

式中：Um——塑性势能；

εj——塑性应变；

σj——塑性应力。

2 能量耗散下的圆度损伤演化分析

剪切系统从初始-应力峰值阶段，剪切带附近颗粒发生翻滚、错动、平动、破碎、挤压掉落等，顶部及底部颗粒无明显相对运动趋势，忽略不计。对于剪切系统圆度损伤区域主要集中于剪切带，在外力作用下，随剪切系统启动，粒间应力出现各向异性，颗粒产生运动致使颗粒表面棱角磨损圆度增大。

任意粗颗粒基于二维平面形状如图3所示，定义颗粒为n边形，按表面凸起棱角，可将颗粒二维表面划分为由n/2个三角形构成。针对颗粒在剪切过程中，因颗粒内部塑性势能汇聚形成微裂纹，裂纹一旦贯通，由图3可知，颗粒初始棱角面积为定值，颗粒边界微裂纹贯通产生棱角磨损，颗粒棱角面积逐渐减小，当颗粒棱角逐渐磨损至近似于内切圆，总面积无限趋近于内切圆面积其圆度值最大。因能量沿最易路径传递，颗粒受粒间应力，塑性势能汇聚引起的微裂纹贯通先发生于颗粒边界，一旦颗粒中部微裂纹贯通颗粒产生核心区域破碎。颗粒在能量汇聚过程中，表面棱角逐渐被磨损，从而改变颗粒圆度，圆度在能量耗散、传递过程中损伤演化。定义粗颗粒圆度损伤因子Dr,棱角面积减少量D，初始面积为D0。

(6)

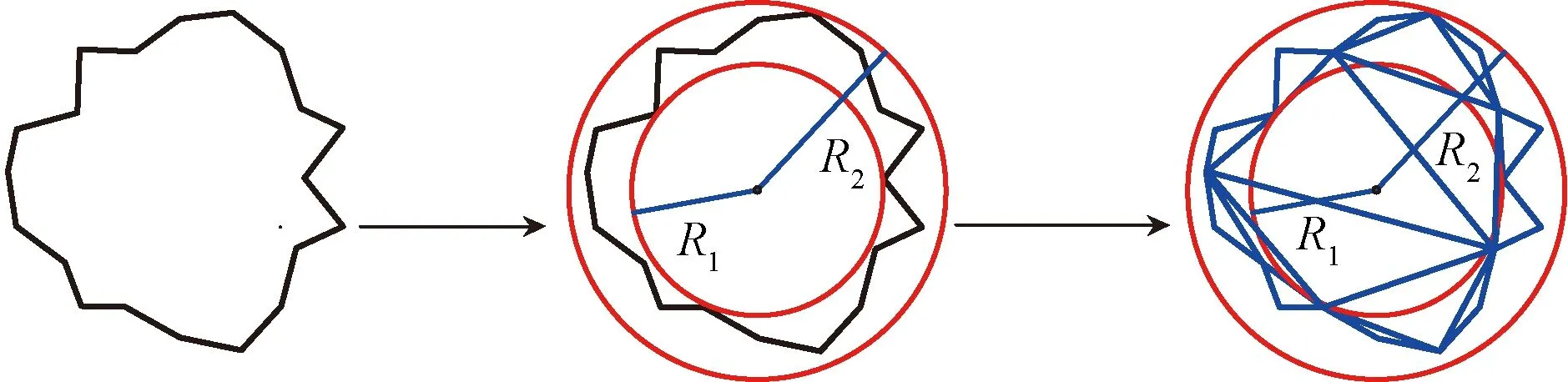
图3 颗粒圆度损伤几何计算示意图Fig.3 Schematic diagram showing geometric calculation of particle roundness damage

应力集中产生的塑性势能，主要贡献于颗粒边界处微裂纹贯通，导致颗粒磨损与颗粒核心区裂纹贯通，使颗粒大面积破碎。引起颗粒圆度损伤的塑性势能主要为棱角磨损部分能量，其值远小于使颗粒核心区破碎的塑性势能，这部分因圆度损伤所需消耗的能量与总塑性势能比值为圆度损伤因子Dr值。颗粒产生应力集中塑性势能为Um，因圆度损伤单个颗粒所需能量为Uf。

Uf=UmDr

(7)

由式(5)可知，针对颗粒单体而言，剪切中塑性区不断贯通，塑性势能不断增大，圆度损伤宏观体现在粗颗粒表面微裂纹演化，致使颗粒在剪切过程中磨损，以磨屑形式从表面剥落。汇聚于颗粒棱角处的塑性势能用于棱角处微裂纹贯通，这部分能量为圆度损伤所需能量。一部分用于颗粒核心区附近微裂纹贯通，使颗粒大面积产生破碎。基于最小耗能原理(最小熵产生原理)[22]颗粒破碎时，应力集中现象被释缓，单个颗粒任意时间t的颗粒破碎耗能率为：

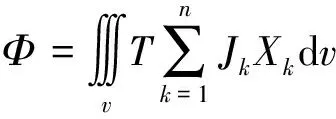
(8)

式中：T，Jk，Xk——微小单位体积在瞬时t的绝对温度、相对应的“流”、相对应的“力”。

颗粒核心区域主裂纹贯通，使颗粒大面积产生破碎所消耗的塑性势能用Us表示，总耗能率为时间函数，对总耗能率积分得：

(9)

根据式(7)～(9)可知，单个颗粒剪切过程中塑性势能Um可表示为：

(10)

此时对于单个粗颗粒总能量可表示为：

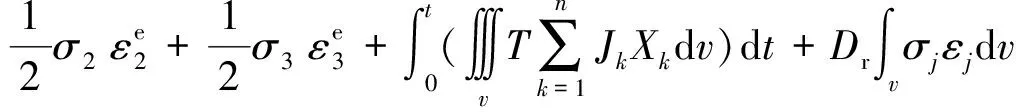
(11)

式(11)为单个颗粒圆度损伤因子的能量演化关系，单个颗粒受到总能量大部分转变为弹性势能，少部分转变为塑性势能，在粗颗粒中形成塑性区，剪切过程中塑性区发育，产生微裂纹，棱角处微裂纹贯通，棱角被磨损，圆度持续损伤演化，粗颗粒主裂纹贯通颗粒破碎。

将式(5)代入式(10)可建立基于能量耗散机制下圆度损伤模型：

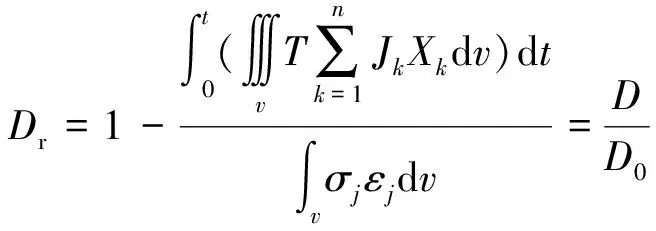
(12)

3 损伤模型的试验研究

试验研究采用可视化剪切仪，选择初始圆度较小的花岗岩颗粒与圆度较大的鹅卵石颗粒进行试验，可根据磨圆度将其分为棱角型接触、圆型接触两类颗粒。为减小颗粒间及试样间尺寸效应影响，控制试验所用粗颗最大高度不超过剪切盒高度的1/20[23]。实验前对颗粒进行筛分试验，选用级配较好的颗粒组进行试验。剪切过程中，颗粒之间接触力、受力面积等发生改变，颗粒产生一定的转角和位移，尤其剪切带内颗粒表现明显。考虑到边界效应对试验结果的影响，剪切过程中，对颗粒剪切带核心区域粗颗粒进行标记，运用image-pro对剪切粗颗粒提取信息数据，探究粗颗粒剪切过程中圆度损伤与力学特性响应。开展法向应力分别为100 kPa，200 kPa，300 kPa的室内试验，获得应力-位移统计表(表1)。

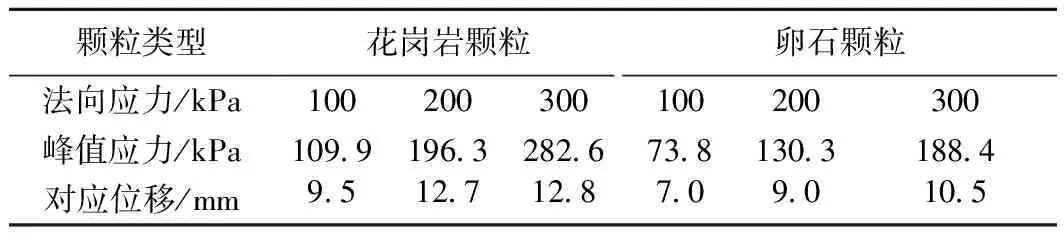
表1 峰值应力-位移统计

通过整理试验数据得到不同颗粒类型下各组试样破坏时的库伦强度拟合直线，由室内试验得到数值拟合曲线，如图4所示。

图4 两类粗粒土强度拟合直线Fig.4 Fitting of strength of two types of coarse-grained soil

通过强度特性剪切试验结果表明，棱角型接触式粗粒土强度参数值大于圆型，抗剪强度大。根据粗粒土剪切过程能量耗散关系，对于圆度较小的颗粒，剪切过程中对应颗粒转动动能、平动动能等发生改变。传递到颗粒内部积聚的塑性势能较大，剪切过程中，更易产生微裂纹及使颗粒产生磨损，增大颗粒圆度。根据式(12)圆度损伤模型可知，圆度损伤因子Dr值增大，导致所需圆度损伤能增大，圆度损伤所需能量的定量变化是影响粗粒土力学特性呈现差异性的根本因素。

根据圆度损伤模型，采用MATLAB对模型进行分析，根据试验结果花岗岩颗粒圆度较小，在试验过程中，其圆度损伤较大，观测效果更明显。同一直剪系统下，达到剪切峰值临界状态一定，粗粒土在剪切过程中满足热力学第一定律，基于能量耗散机制下相同法向应力的圆度损伤值无限趋近。针对花岗岩颗粒拟合三种法向应力下圆度损伤因子(Dr)、圆度损伤所需能量(Uf)、剪切位移(S)散点图如5所示。在法向应力分别为100 Pka，200 kPa，300 kPa下，Dr=1%，Dr=0.805%，Dr=0.374%时，散点图基于三维空间第一次出现拐点，此时对应的Uf=0.035，S=0.59。Uf=0.018，S=0.25，Uf=0.007，S=0.18。

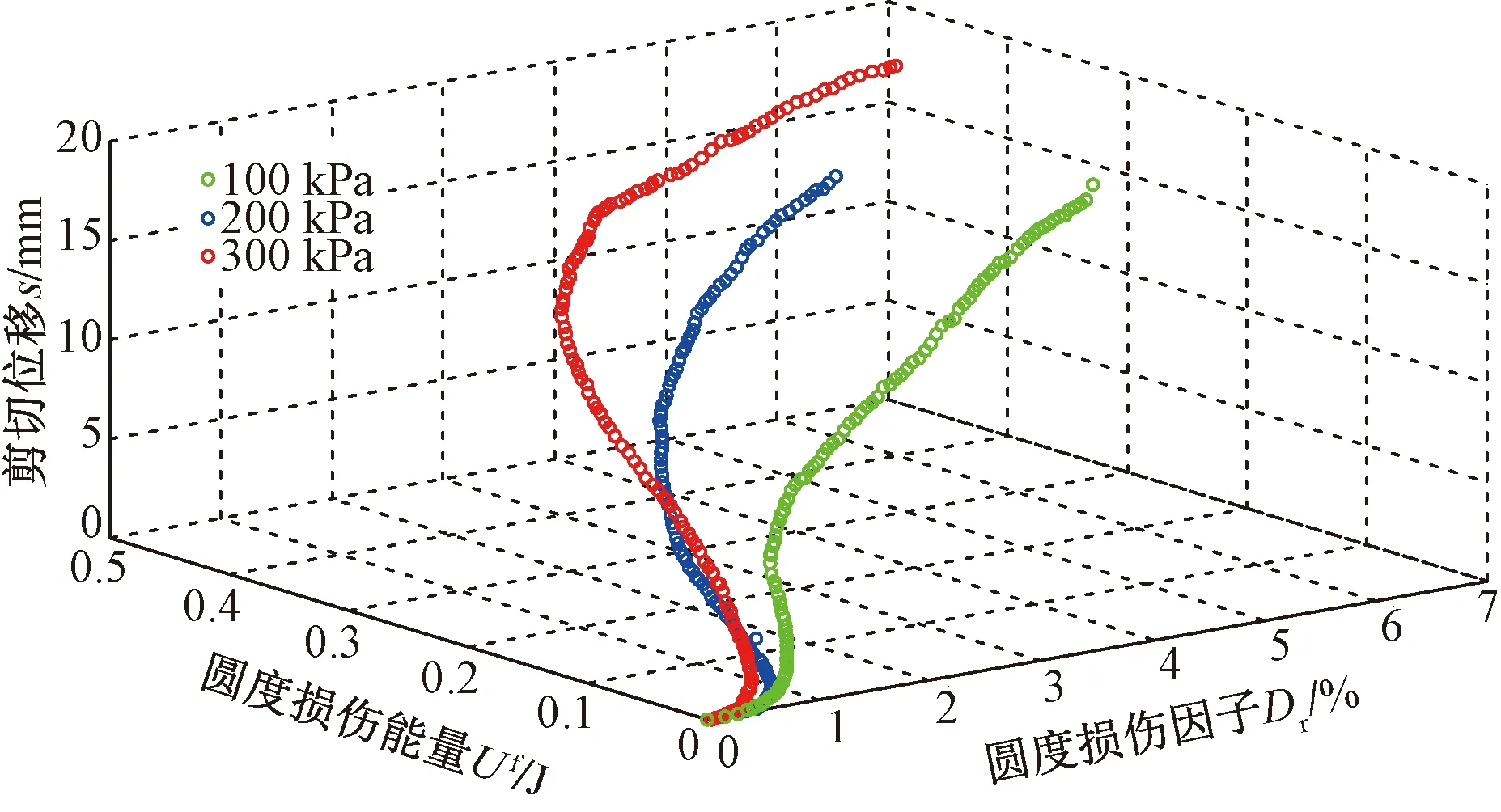
图5 圆度损伤因子与能量、剪切位移散点图Fig.5 Roundness damage and scatter plot of energy and shear displacement

花岗岩剪切过程圆度损伤基于100 kPa，200 kPa，300 kPa下存在差异，圆度损伤随法向应力增大，与颗粒力学特性响应速度越快。如图5所示，剪切过程出现了2次较大拐点，用T1，T2表示。2次拐点对应的Uf、Dr、S如表2所示。

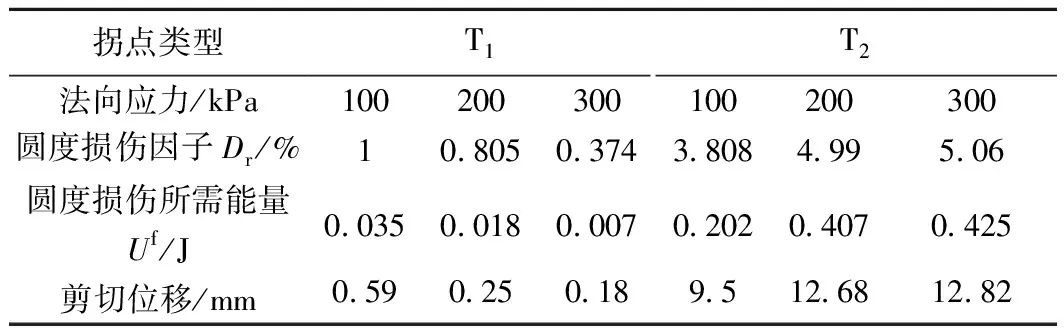
表2 剪切过程圆度损伤拐点特征值统计

由图5、表2可知，第一次圆度损伤过程出现拐点，随法向应力增大出现拐点延迟，此阶段为粗颗粒在试验条件下颗粒间粒间应力急剧变化的结果，圆度损伤因子急剧增大宏观体现于剪切盒内颗粒所处状态的改变。随着剪切行为的持续，达到应力峰值，第二次出现拐点，传递到颗粒内部的弹塑性势能逐渐汇聚，塑性势能的产生使颗粒产生微裂纹。达到应力峰值时，单个颗粒塑性区发育，微裂纹贯通，塑性势能达到最大。当圆度增大后，颗粒棱角已被磨损，继续进行剪切，圆度损伤逐渐达到稳定状态。

法向应力对粗粒土圆度损伤具有一定影响[24]，主要原因为法向应力大小不同，对传递到颗粒内部应力大小存在差异，粒间应力大小的改变对粗粒土在试验过程中具有不同程度的束缚作用[25]，从而影响着粗粒土剪切过程中圆度损伤程度。如图6圆度损伤因子与圆度损伤所需能量所示。

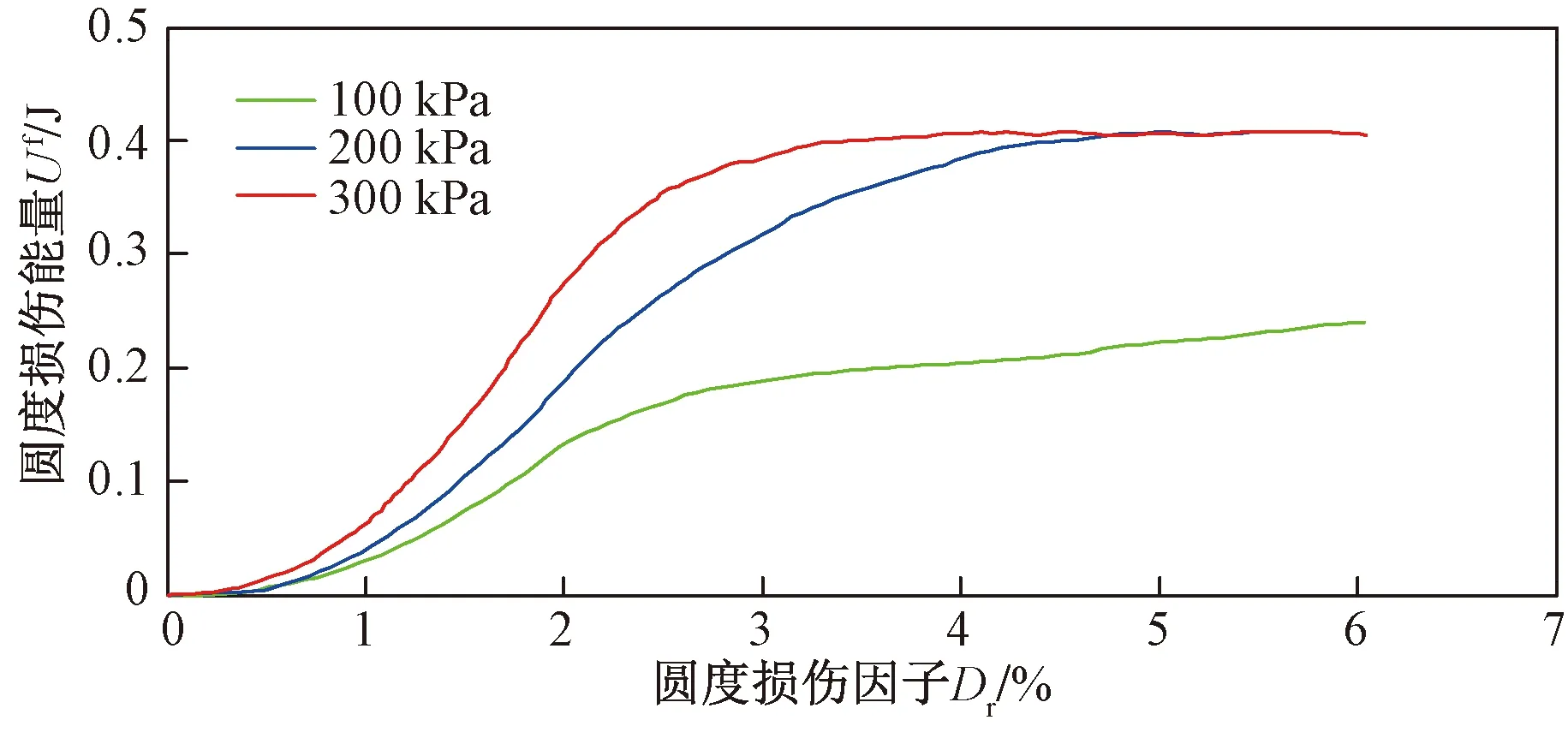
图6 圆度损伤与能量关系图Fig.6 Roundness damage and energy diagram

100 kPa下，Dr=6%时，Uf=0.239且尚未趋于稳定。200 kPa时，Dr=4.794%，Uf=0.405。300 kPa时，Dr=4.046%，Uf=0.407。所需圆度损伤能量已趋于稳定。试验结果表明针对同一颗粒，达到峰值状态圆度损伤因子随法向应力增大而减小，所需的圆度损伤能增大。

将同一法向应力下，颗粒剪切过程圆度损伤过程分为3个阶段。第一个阶段为圆度损伤响应阶段，即为第一次出现损伤拐点，此阶段粗颗粒圆度损伤对粒间应力的突然变化做出响应。第二个阶段为圆度损伤演化阶段，即到第二次出现拐点应力达到峰值时，此阶段粗颗粒塑性势能急剧增大，颗粒表面微裂纹持续演化，对应曲线变化较大。第三个阶段为圆度损伤稳定阶段，随着剪切持续进行，损伤因子增大，但损伤演化阶段峰值微裂纹已贯通，塑性势能大部分以颗粒表面能用于裂纹贯通，形成新的颗粒表面，在剪切未结束前颗粒继续错动、翻滚、平动等运动，不断磨损，损伤因子继续增大。