鄂尔多斯高原湖泊蒸发原位试验研究
2019-10-14许文豪王晓勇尹立河贾伍慧朱立峰董佳秋孙芳强
许文豪,王晓勇,张 俊,尹立河,贾伍慧,朱立峰,董佳秋,孙芳强
(1.中国地质大学(北京)水资源与环境学院,北京 100083;2.中国地质调查局西安地质调查中心,陕西 西安 710054)
水面蒸发是自然界中水循环和水量平衡的重要环节,几乎所有有关水资源和农业问题的研究,都离不开水面蒸发的分析与计算[1]。在干旱-半干旱地区,降水量较少而蒸发强烈,水资源紧缺,生态环境脆弱,水面蒸发的研究对于认识区域气候、揭示水循环机理、评价水资源以及生态系统的评估管理等具有重要意义[2]。
由于观测大水面蒸发量十分困难,国内外对自然水面蒸发直接观测较少,有前人在大型水体中通过涡度相关系统观测水面蒸发[3-4]。国外有研究采用水面漂浮蒸发皿实测小型水体蒸发[5],研究表明水体中原位试验测量蒸发明显低于陆面条件蒸发观测,开展原位试验观测蒸发更接近于水面实际蒸发。由于实测资料有限,水面蒸发量确定比较困难[6-7],目前,通常是通过观测小面积水面蒸发折算后间接推求大面积的水面蒸发,即蒸发器(皿)折算法[1]。折算法一般使用不同直径的蒸发器(皿)(如E-601型蒸发器、φ20 cm蒸发皿)观测的数据[8],通过折算系数校正获取水面蒸发量,如王永义经计算检验表明采用折算法具有可推广性[9],何渊等研究鄂尔多斯盆地沙漠高原区湖泊蒸发选用E-601型和φ20 cm蒸发皿监测蒸发数据[10]。蒸发器(皿)测量一般在陆面条件下进行,蒸发器及周围空气的动力及热力条件与水体有很大不同,测得的蒸发量不能代表自然界真实的蒸发量。同时,由于蒸发皿折算系数受多种因素影响且随季节变化[3,11],即使通过折算系数进行校正,但也不能获得水面蒸发的精确值。计算水面蒸发的另一种主要方法是通过各种蒸发模型计算理论值,常用的有Penman公式、Jesen-Haise公式及经验公式等。不同的公式方法存在约束条件,推广应用收到一定的限制,如Penman公式需要较全的气象数据等[12],通过计算所得的理论蒸发量同样不能代表水体的真实蒸发量。
鄂尔多斯高原位于干旱-半干旱地区,特殊的地质条件与内陆水循环的封闭性形成了众多湖泊,水体是水资源的重要组成部分,也是湖泊生态系统的重要组成部分。该地区湖泊主要接受地下水补给,湖面蒸发是湖泊唯一的排泄方式。因此,湖泊蒸发是区域水循环的关键过程,对水文循环研究有重要意义。同时,湖泊蒸发作为区域水平衡中重要均衡项,是准确评价水资源的关键项。因此,湖水蒸发研究对于认识区域水循环、水资源计算评价和湖泊生态环境保护等方面有着重要的科学价值和现实意义[13]。
本次研究选择鄂尔多斯高原木凯淖为典型湖泊,开展湖泊蒸发原位试验研究,通过湖泊蒸发量实测,分析蒸发量与各个气象要素之间的相关性,确定湖泊蒸发的影响因子,为鄂尔多斯高原湖水蒸发机理研究提供基础依据。通过湖面原位实测与陆面不同条件蒸发试验对比,获取适合本地区小型蒸发皿与湖水蒸发的折算系数,并通过与Penman公式计算蒸发量对比,分析Penman公式在本地区的适用性,为该地区湖泊蒸发提供依据和参考。
1 材料与方法
1.1 研究区概况
鄂尔多斯高原位于我国内蒙古自治区西南部,总面积约13×104km2。鄂尔多斯高原属干旱-半干旱大陆性气候,多年平均降水量约300 mm,该区降水较少且主要集中在夏季,蒸发强烈,年均潜在蒸发量是降水量的7倍。鄂尔多斯高原地势从西北向东南缓慢倾斜,海拔在1 300~1 500 m。北部为库布其沙漠,南部为毛乌素沙漠和滩地,中部隆起,海拔1 400~1 700 m,为鄂尔多斯台地。鄂尔多斯高原分布有大量湖泊,大多数为咸水湖泊,溶解性总固体较高,且湖水深度较浅。由于干旱少雨,蒸发量大,大多湖泊水质较差。尤其在毛乌素沙漠,湖泊更为多见,集水面积在1 km2以上的湖泊有近70个[10,14-15]。
本次研究选在鄂尔多斯高原较为典型的湖泊——木凯淖开展湖泊蒸发原位试验研究。木凯淖地处毛乌素沙漠北缘,属典型的干旱-半干旱气候。湖面海拔约1 370 m,面积约2 km2,湖水水深0.3~1 m,随季节波动,湖水溶解性总固体约1.5g/L。根据距离木凯淖最近的乌审召气象站的长期气象资料(2000—2017年)显示,年平均降水量330 mm,年变化系数为0.3,70%以上的降水发生在6—9月。φ20 cm蒸发皿测得的年平均蒸发量2 289 mm。
1.2 原位试验方法
1.2.1试验方案
为测得木凯淖湖水蒸发量,本次研究在湖中心位置放置E-601型蒸发器,以钢架平台固定(图1),保持蒸发器平稳。为避免盐度变化对蒸发的影响,蒸发器中加入浅层湖水,每隔3~4d进行人工换水,首先将蒸发皿中经过蒸发的湖水全部清空,然后重新加入湖水至与湖水面齐平,以避免蒸发富集引起的湖水盐度增加对蒸发的影响。在人工换水前后,人工测量换水前后蒸发皿中水位,用以对比校正蒸发皿中水位计监测数据。另外,为对比湖水蒸发和陆面蒸发以及咸淡水等不同条件下的蒸发量,在湖泊附近的空旷位置安装两个φ20 cm小型蒸发皿,用支架固定,器口距地面70 cm。两个蒸发皿分别加入湖水和淡水,用来观测不同盐度对蒸发量的影响。小型蒸发皿中水位高度7 cm,维持蒸发在5d以上,加水间隔为3~4d。原位试验观测时间为2017年6月9日—9月9日。
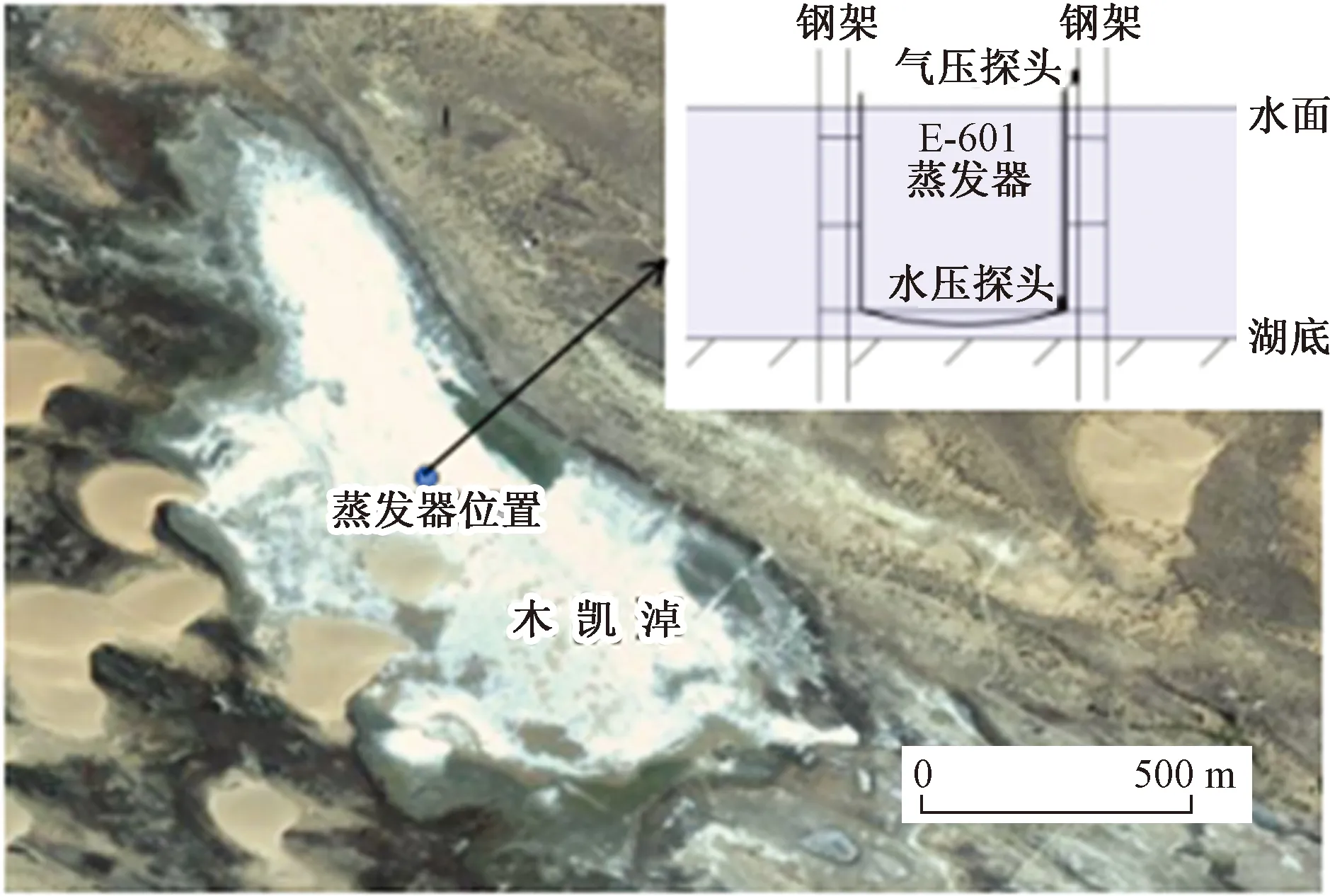
图1 研究区位置及原位试验图Fig.1 Location of the study and in-situ test
1.2.2数据获取
在E-601蒸发器底部安装测量精度±1 mm的水压力传感器(Keller DCX-22A,Winterthur,Switzerland),Keller同时配有气压传感器探头,固定于钢架平台。Keller监测气温和水温数据,监测间隔为1h。在距离木凯淖湖边200 m处放置自动雨量筒(52203 RM Young rain gauge, R.M. Young Co.,Michigan,USA),安装高度为70 cm,测量精度0.2 mm,监测降雨量数据。同时,收集乌审召气象站(木凯淖东南20 km)湿度、风速等气象要素的日平均数据。另外从Earth Data数据网站下载日净辐射数据(https://disc.gsfc.nasa.gov/datasets?keywords=GLDAS),空间精度0.25°×0.25°,时间间隔3h。
计算通过E-601蒸发器中水压与气压差值分别获取该时段初和时段末的水位,水位差值加上该时段内的降雨量得到蒸发实测值。如计算日蒸发量:由当天0:00时刻水位与第二天0:00时刻水位的差值加上该天降雨量。
φ20 cm小型蒸发皿每次加水前后用直尺测量水面距皿口高度。计算某一时段小蒸发皿蒸发量:该时段初与时段末的读数差值加上该时段内降雨量。
1.3 多元线性回归分析
湖水蒸发受到多个气象因素的影响,本次研究通过建立多元线性回归模型对湖水蒸发的影响因子进行分析。根据统计学方法[16],首先对因变量和自变量系列数据进行归一化处理:
将归一化后的数据输入SPSS统计分析工具软件中,建立蒸发量与气象要素的多元线性回归模型。采用逐步回归分析方法进行变量引入。逐步回归分析法可以从相关性很强的多个自变量中选择最显著的因子放入回归模型,避免多重共线性问题[17]。采用F检验概率值作为判断标准,使用系统默认值,进入概率小于等于0.05,移出概率大于等于0.1。
1.4 水面蒸发彭曼公式
在计算水面蒸发的模拟公式中,最常用的方法是Penman公式[2]:
式中:E——水面蒸发量/(mm·d-1);
Rn——净辐射的蒸发当量/(mm·d-1);
Ea——干燥力/(mm·d-1);
Δ——饱和水汽压与温度曲线的斜率/(hPa· ℃-1);
γ——干湿球常数/(hPa· ℃-1)。
1.5 Nash效率系数
Nash效率系数(Nash-Sutcliffe efficiency coefficient)简称NSE,一般用来验证水文模型结果:
式中:Q0——观测值;
Qm——模拟值;
Qt——t时刻值;
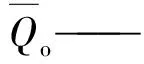
NSE接近1,表示模型精度高,可信度较高;NSE接近0,表示模拟结果接近观测值平均值水平,即总体结果可信,但模拟误差较大;NSE小于0,则模型不可信,模拟失败。
2 结果分析
2.1 蒸发量变化及影响因素分析
2.1.1日蒸发量及气象因素变化特征
日蒸发量及降水量随时间变化见图2(a)。观测期内木凯淖实测总蒸发量603.3 mm,平均日蒸发量6.49 mm,变差系数(CV)0.43,日蒸发量波动剧烈,最大日蒸发量接近13 mm,最小不足1 mm,蒸发强烈时日蒸发量可达蒸发弱时的17倍。观测期内,日蒸发量的整体变化趋势从6月中旬至7月中旬呈上升趋势,在7月下旬出现一系列低值,而这段时期降雨量大,8月上旬恢复较高的蒸发,至9月上旬日蒸发量呈现下降趋势(图3)。
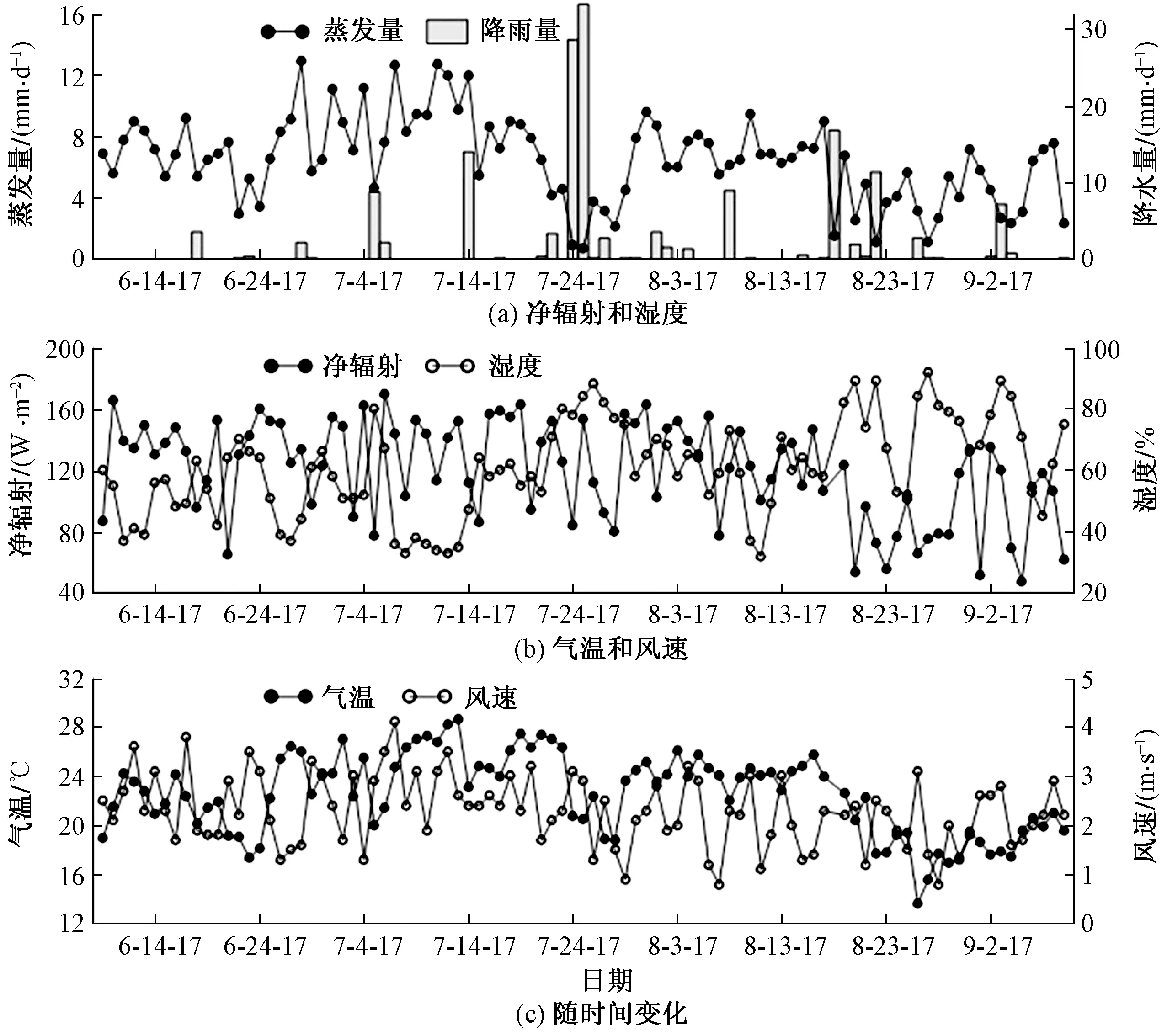
图2 日蒸发量和降水量(a)、净辐射和湿度(b)、气温和风速(c)随时间变化图Fig.2 Temporal variations in (a) daily evaporation and precipitation, (b) net radiation and humidity, and (c) air temperature and wind speed
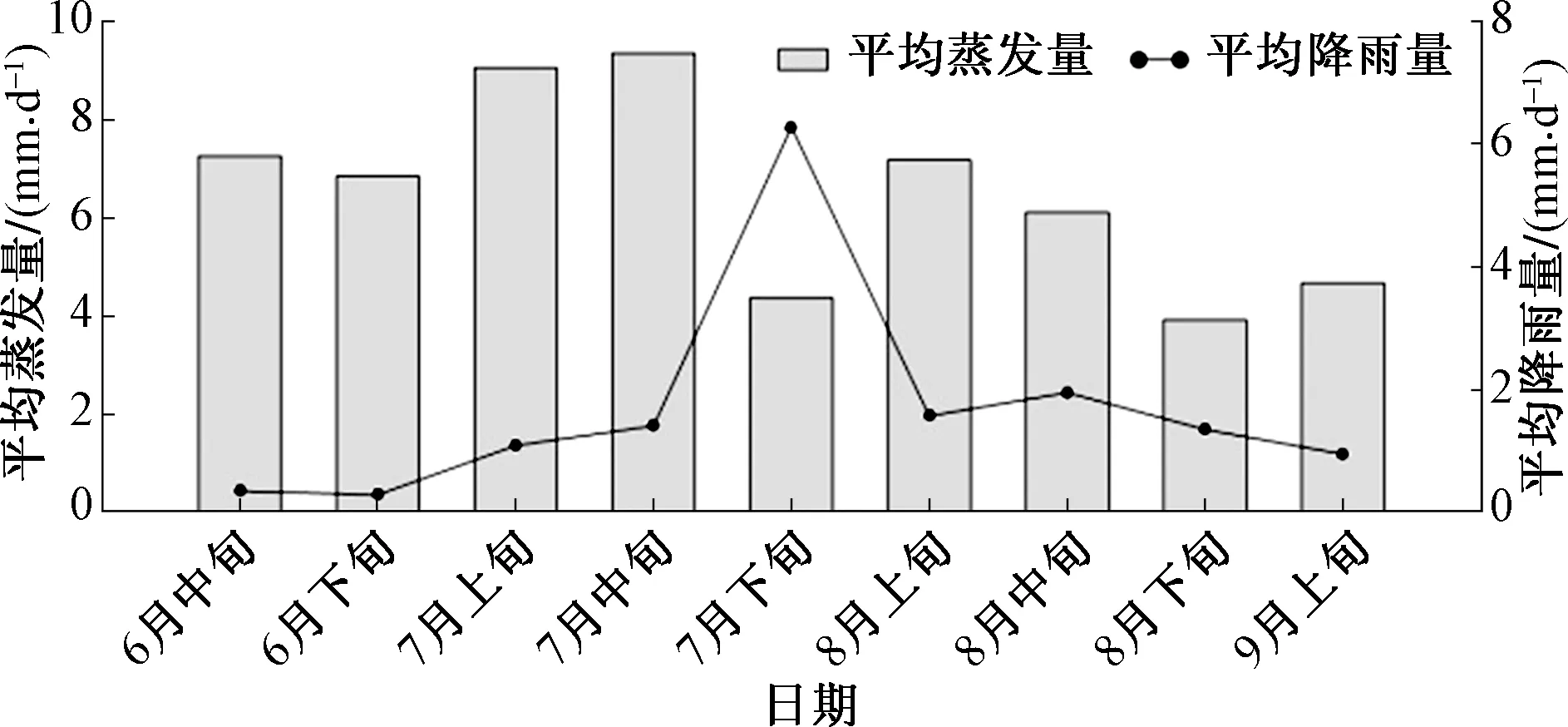
图3 旬平均蒸发量与降雨量Fig.3 Average evaporation and precipitation at ten-day’s scale
观测期内有降水天数35d,占总天数的38%,总降水量159.8 mm。一般在降水较多时对应微弱的蒸发,7月下旬平均日降雨量较大,对应的该时段内湖水蒸发较少,平均日蒸发量较低。
观测期内日平均湿度及净辐射随时间变化过程见图2(b)。日平均湿度从6月上旬到7月中旬整体下降,而在7月下旬日平均湿度较高,到8月上旬恢复到较低值后整体呈上升趋势。这与日蒸发量的变化呈现相反的趋势。日平均净辐射在47.40~169.71 W/m2间波动,其波动趋势整体上与湿度呈现一定的负相关。
由日平均气温和风速随时间变化(图2(c))可以看出,日平均气温在整体趋势上,由6月上旬到7月中旬不断上升,在7月下旬下降,8上旬恢复较高气温后到9月上旬呈现整体下降趋势。这与日蒸发量的波动规律相似。观测期内日平均风速随时间在0.8~4.1 m/s之间上下波动。
2.1.2日蒸发量与气象因素相关分析
日蒸发量与气象因素的波动规律存在一定的相关性。将日蒸发量与各气象要素日平均值进行相关分析,见图4。通过散点图拟合线性方程,根据决定系数大小,蒸发量与湿度的相关性最好(R2=0.59,p<0.01),与气温的相关性次之(R2=0.47,p<0.01)。蒸发量与净辐射也呈现较好的相关性,其R2为0.23,p<0.01。而蒸发量与风速相关性较差,R2为0.05,p<0.05。
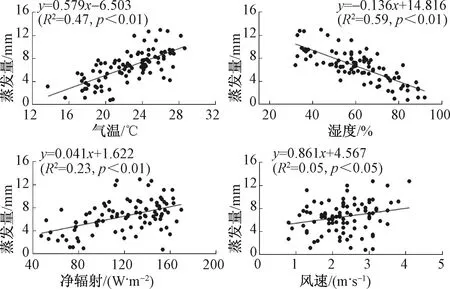
图4 日蒸发量与气温、湿度、净辐射及风速关系图Fig.4 Relationship between daily evaporation and air temperature, humidity, net radiation and wind speed
由此可见,蒸发受湿度影响最大,日平均湿度较大一般对应较小的蒸发;受气温影响次之,气温越高则蒸发越强烈。在日尺度上净辐射对蒸发的影响程度一般。此次研究发现,在日尺度上蒸发量与风速相关性很弱,可能原因是风速在一天内被平均后对湖水蒸发的影响淡化。
2.1.3多元线性回归模型
日蒸发量和气温、湿度、净辐射、风速日平均数据建立的多元线性回归模型为:
E0=-0.462ρ+0.373TA+0.178Sw+0.395
式中:E0——日蒸发量;
ρ——湿度;
TA——气温;
Sw——表示风速。
回归方程的决定系数R2=0.69,说明模型拟合度好。模拟结果采用Nash效率系数NSE评价。利用多元线性回归模型得到的蒸发量模拟值与实测日蒸发量计算多元线性回归模型NSE=0.69,证明模拟效果较好。模型结果中包含湿度、气温、风速,剔除了净辐射,对湖水蒸发影响显著性排序依次为湿度、气温和风速。湿度和气温是对湖水蒸发影响最大的前两个因素,这与相关分析法得出的结论一致。
2.2 不同方法蒸发量对比
2.2.1不同试验条件蒸发量对比
将不同试验条件下的φ20 cm蒸发皿蒸发量与湖内蒸发量进行对比,见表1。观测期内总蒸发量湖内最小,累计蒸发129.4 mm,湖边陆面加入淡水和湖水的小型蒸发皿分别累计蒸发152.4 mm、151.4 mm,蒸发量接近一致。逐时段内,湖内蒸发量均小于湖边陆面小型蒸发皿蒸发量,湖边陆面小型蒸发皿蒸发量差值很小。日平均蒸发量湖内8.6 mm,约为湖边陆面φ20 cm蒸发皿的85%。
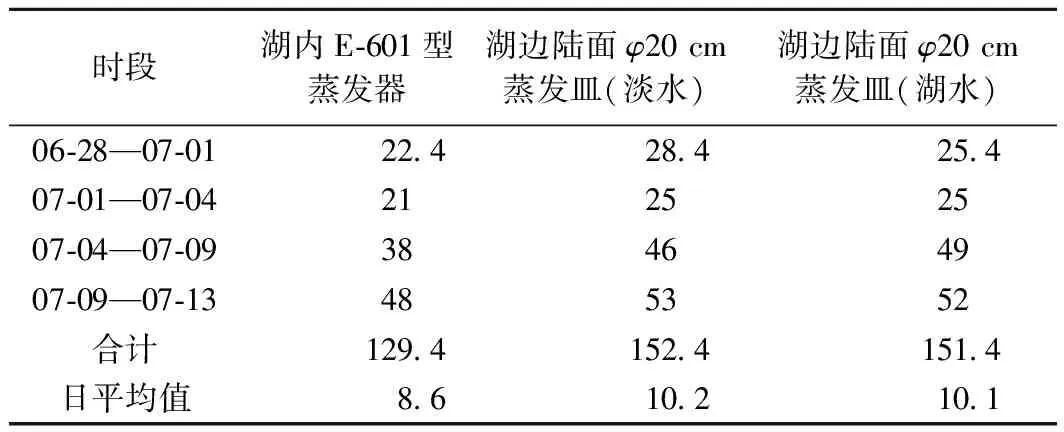
表1 不同试验条件累计蒸发量
蒸发皿加入淡水和湖水蒸发量一致,可见蒸发皿中水的蒸发受盐度(<1.5g/L)影响较小,可以忽略。湖内蒸发量均小于湖边陆面小型蒸发皿蒸发量。水体条件下,由于水面大量水分蒸发,其湿度一般大于陆面条件,另外随着气温上升,大水体水温的增长幅度远小于小型蒸发皿中的水温,因此水面实际蒸发小于小型蒸发皿中水分蒸发。根据小型蒸发皿换算湖水蒸发需折算系数的校正,本次研究表明,木凯淖湖泊蒸发与湖边φ20 cm小型蒸发皿的折算系数约为0.85。
2.2.2与Penman公式对比
将逐日蒸发量与Penman公式计算结果做对比,两者逐日变化见图5(a)。Penman公式计算累计蒸发533.1 mm,日平均5.79 mm(实测值分别为603.3 mm、6.49 mm),均略低于实测值。Penman公式计算值波动幅度较小,最大日蒸发量9.8 mm,最小日蒸发量2.1 mm,CV为0.26;实测日蒸发量波动幅度较大,CV达到0.43。蒸发很强烈时,如在7月11日和12日蒸发量均相对较高,实测蒸发量高于Penman公式计算值;而在蒸发很微弱时,如7月24日和25日蒸发量均相对很低,实测值则低于计算值。
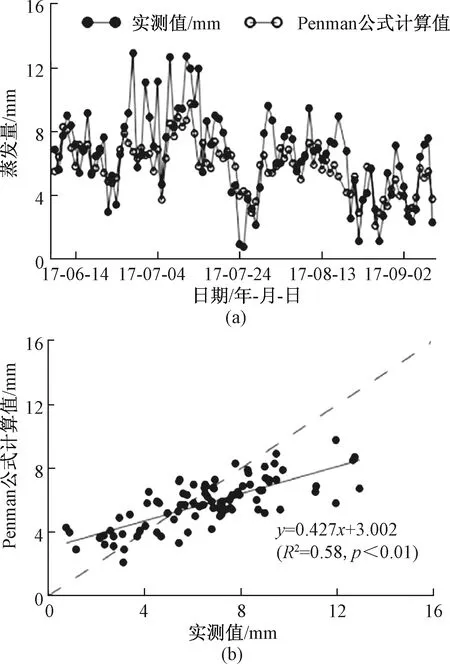
图5 实测日蒸发量与Penman公式计算结果动态曲线及关系图Fig.5 Dynamic variation (a) and relationship (b) between the observed results and estimated results by using the Penman Equation for daily evaporation
由图5(b)可以看出,实测蒸发量和Penman公式计算值相关系数R2=0.58,p<0.01,相关性较好。计算Nash效率系数NSE=0.46,说明使用Penman公式计算日蒸发量效果较好。当蒸发量偏离平均值时,使用Penman公式存在误差;当蒸发很弱时,使用Penman公式高估湖水蒸发,计算日蒸发量偏大;当蒸发强烈时,使用Penman公式低估湖水蒸发,计算结果偏低。
3 讨论
3.1 蒸发量与气象因素相关性
湖水蒸发受多个气象因素的影响,大量研究表明,影响干旱-半干旱水面蒸发的因素包括气温、水汽压差、风速、湿度和辐射等[2,10,18]。通过相关和多元统计回归模型两种方法分析,结果表明日蒸发量与湿度、气温、净辐射和风速间有一定的相关性,这与前人的结论一致。
研究显示,不同因素对蒸发影响的显著性中蒸发量受气温影响较显著,与其他前人研究结论一致,如徐仁通过通径分析得出平均气温是水面蒸发量的主要影响因素[19],李慧菁采用影响因子分析法得出气温对水面蒸发影响占主要地位等[20]。本次研究表明,湿度对湖水蒸发影响显著。对于湿度与水面蒸发相关性,目前有不同观点,有些学者认为,蒸发与湿度相关性大,如方晓明等通过研究表明日蒸发量与日均相对湿度显著负相关[21],而有些学者认为蒸发受湿度影响不明显[18]。
3.2 与小型蒸发皿对比
本次研究表明,湖内蒸发量小于陆面小型蒸发皿观测蒸发量,这符合普遍认为的小型蒸发皿观测蒸发量大于水面实际蒸发的规律[1],如Masoner J R在美国的研究表明,实测蒸发速率明显小于陆面蒸发皿蒸发速率[5]。水面蒸发与小型蒸发皿折算系数在各个地区不同季节取值不一[22]。本次研究表明鄂尔多斯高原地区夏季湖水蒸发与φ20 cm小型蒸发皿的折算系数约为0.85。根据前人研究,黄河流域干旱半干旱地区6—9月小型蒸发皿与20 m2蒸发池(近似代表湖泊蒸发)的折算系数多年平均值介于0.634~0.677[23],本次结果偏高。不同的结果与试验方法有关,本次在湖泊内部进行原位试验,所得折算系数对本地区具有一定的参考性。
此次研究发现小型蒸发皿中加入水的盐度(<1.5 g/L)对湖水蒸发量影响不大,可以忽略。这与前人在本地区的研究结论一致[10],并符合李阳等在干旱地区盐度水面蒸发试验研究得出的规律,水体盐度在0.8~10g/L范围内对蒸发量影响较小[24]。
3.3 Penman公式适用性
Penman公式是国内计算水面蒸发时常用的方法,然而对于不同的地区,其适用性存在差别。有些研究发现, Penman公式计算结果与蒸发实测值接近,精度较高,如前人在半干旱沙地-草甸区[2]的研究,而有些学者研究表明 Penman公式模拟水面蒸发效果较差,如韩鹏飞等在巴丹吉林沙漠的研究[17]。本次研究将实测湖泊蒸发量与Penman公式计算结果进行对比,发现两者相关性较高,效果较好。
4 结论
(1)鄂尔多斯高原湖泊水面蒸发受湿度、气温影响最大。
(2)小型蒸发皿监测蒸发量高于湖泊蒸发,与湖水蒸发折算系数为0.85。小型蒸发皿中加入湖水和淡水蒸发量无明显差距,水的盐度(<1.5g/L)对湖水蒸发影响很小,可以忽略。
(3)使用Penman公式估算湖泊蒸发量效果尚好。当蒸发很弱时,使用Penman公式计算日蒸发量偏大,而当蒸发强烈时,使用Penman公式计算结果则偏低。
受限于本次原位试验观测时段,未能就湖泊年蒸发量进行分析和讨论,后续工作将延长观测期,以深入分析不同季节的蒸发量变化规律及影响因素。
