基于变形-结构法的隧道初期支护安全性评价研究
2019-10-14刘大刚王明年
杨 涅, 刘大刚, 王明年, *,于 丽
(1. 西南交通大学土木工程学院, 四川 成都 610031;2. 西南交通大学 交通隧道工程教育部重点实验室, 四川 成都 610031)
0 引言
隧道开挖后,为控制围岩应力适量释放和围岩变形,同时也为增加结构的安全度和方便施工,往往需要施作初期支护。在现行隧道工程中,初期支护承担荷载比例大,而二次衬砌一般作为考虑荷载长期效益的安全储备,因此初期支护的合理设计至关重要。初期支护设计包括隧道施工前的预设计和施工中的动态设计,而初期支护的安全性评价又是实现初期支护动态设计的关键,故有必要进行初期支护安全性评价研究。
目前,众多专家学者已对初期支护的力学行为开展了大量深入的研究,提出了多种初期支护安全性评价方法。Vojkan等[1]通过现场监测及室内试验,研究了钢纤维喷射混凝土初期支护与围岩共同作用的力学性能; 徐帮树等[2]通过初期支护位移反演围岩的力学参数,进而通过地层-结构法计算初期支护的内力,并依据型钢混凝土安全系数计算方法进行安全性评价; 李洪泉等[3]基于线弹性、小变形和平截面等假设,推导了依据初期支护位移求支护内力的计算方法,并给出了初期支护截面失效的功能函数; Oreste[4]采用负指数函数拟合喷混凝土强度随时间的增长关系; 扈世民[5]采用理论分析、数值模拟及现场试验等手段,基于收敛-约束法原理,对依托工程初期支护安全性进行了评价; 杨成永等[6]依据修正GL2000徐变模型,提出了基于测量初期支护位移并考虑徐变影响的支护内力计算公式; 刘光明等[7]基于剪切滑移理论,确定了初期支护安全性评价方法,并对典型偏压隧道初期支护参数进行了优化。由上述文献可知,有关初期支护安全性评价方法的研究成果已很丰富,但由于理论较为复杂、部分参数选取困难等原因,一定程度上使这些方法的推广应用受到了限制。目前,基于荷载-结构法的初期支护安全系数评价法,由于其物理模型简单,可进行多种荷载、多种岩体状态的综合分析,计算速度快,至今仍很通用,但其计算结果是否符合实际,关键是对初期支护所受荷载的正确估算。现行规范中初期支护所受荷载采用围岩松动荷载而非更符合实际情况的形变压力,使得设计上偏保守,经济性较差[8]; 而较之初期支护所受荷载的不确定性,初期支护的变形则具有资料易得、原理清楚的天然优势,且初期支护的变形是隧道开挖支护后,结构在围岩压力和抗力作用下的综合反应,确定隧道结构变形可以唯一确定结构内力。
鉴于上述原因,本文基于矩阵位移法,建立以关键节点位移为已知量的变形-结构法,即在假设的荷载模式下,根据满足分布条件的关键节点的位移值,直接反算结构荷载及内力,进而依据规范定量评价初期支护的安全性; 并编制相应的计算机程序进行工程应用分析,以期为隧道施工阶段基于监控量测数据对初期支护的安全性进行评价提供有益帮助。
1 初期支护变形-结构法
1.1 基本假定
目前采用的初期支护结构方案主要有以下3种: 无系统锚杆支护结构、喷锚组合支护结构、锚杆为主的支护结构。为简化分析,本文所采用的初期支护结构方案为无系统锚杆支护结构,即初期支护主要由素混凝土或钢筋混凝土(或钢架)组成,不设置系统锚杆,仅在局部位置设置锚杆以防止掉块。基于上述初期支护的特点,提出以下基本假定:
1)在进行初期支护结构内力计算时,不考虑锚杆的作用;
2)近似将初期支护视为线弹性体,满足小变形和平截面假定;
3)当仰拱后于拱墙施作时,若施作了锁脚锚杆,则仍考虑仰拱对初期支护结构的贡献,但忽略其与围岩的相互作用;
4)较之隧道横断面尺寸,隧道纵向长度较大,故近似认为隧道纵向位移等于0,隧道初期支护处于平面应变状态。
1.2 变形-结构法的建立
基于矩阵位移法,建立初期支护结构的变形-结构法,流程如图1所示,具体步骤如下。
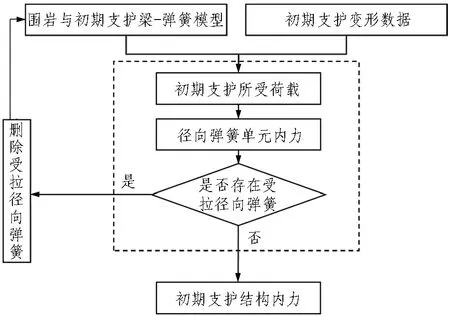
图1 变形-结构法流程图
1.2.1 建立围岩与初期支护的梁-弹簧模型
1)将初期支护离散成n个单位长度的弹性梁单元,并将单元的联结点视为节点;梁单元是既有局部坐标又有整体坐标的二维有限元,其局部(整体)坐标系均为直角坐标系。局部坐标系的x轴与梁轴线重合,x轴正向逆时针旋转90°即得y轴正向;整体坐标系的x轴正向取水平向右方向,y轴正向取竖直向上方向。二者满足如下关系式:
(1)

2)初期支护与围岩间的相互作用,采用径向弹簧单元和切向弹簧单元模拟[9],模型如图2所示。弹簧单元也是既有局部坐标又有整体坐标的二维有限元,局部(整体)坐标系定义与梁单元相同,二者满足如下关系式:
(2)
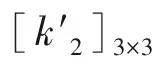
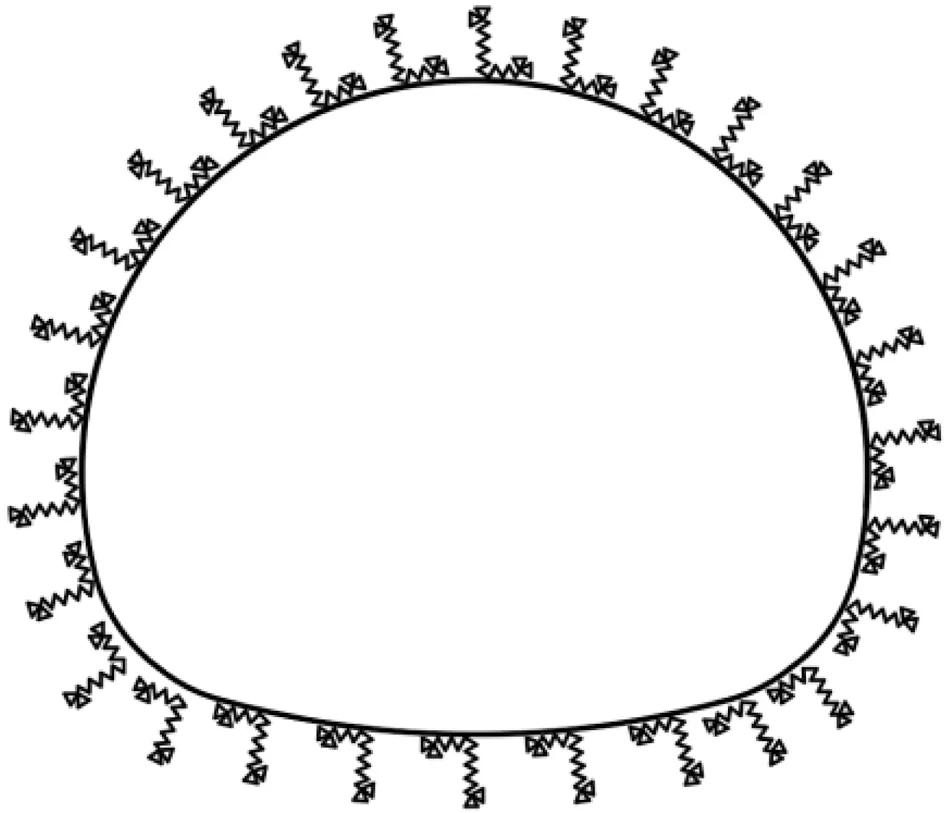
图2 梁-弹簧模型
3)采用直接刚度法,基于2个连续条件——变形协调条件和静力平衡条件,即连接在同一节点的各单元的节点位移应该相等,并等于该节点的结构节点位移;作用于结构上某一节点的荷载必须与该节点上作用的各单元的节点力相平衡[10]。将整体坐标系下各单元刚度矩阵直接组成初期支护结构的总体刚度矩阵,即:
[K]3n×3n=[K1]3n×3n+[K2]3n×3n
(3)
式中: [K]3n×3n为初期支护结构的总体刚度矩阵; [K1]3n×3n为梁单元的总体刚度矩阵; [K2]3n×3n为弹簧单元的总体刚度矩阵。
4)则初期支护结构的有限元基本列式为:
[K]3n×3n[δ]3n×1=[F]3n×1
(4)
式中: [δ]3n×1为初期支护结构节点位移矩阵; [F]3n×1为初期支护结构的等效节点荷载矩阵。
1.2.2 获取初期支护的变形数据
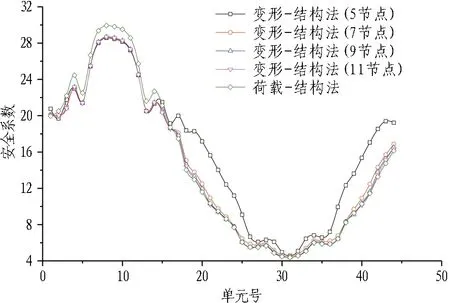
通过全站仪对初期支护结构m(m 1.2.3 计算初期支护结构所受荷载 (5) 2)仅采用m个关键节点位移进行节点荷载计算时,其所得解通常并不具有唯一性。为了使计算得到的解是唯一的,一般需要预先根据工程经验假定隧道荷载的分布形式[11]。基于此,本文以m个关键节点对应的节点荷载,即水平节点力和竖直节点力为代求未知量,其他节点的节点荷载则按相对位置关系进行线性插值确定,式(5)经整理得: (6) 初期支护结构的节点荷载中弯矩值小,将其忽略,计算中弯矩值均取0。求解式(6)即得到初期支护结构的等效节点荷载矩阵[F]3n×1。 3)实际隧道工程中,根据弹性反力的定义,径向弹簧单元仅能受压,需进行径向弹簧的存在性判定[12]。求解式(4),确定初期支护结构的节点位移[δ]3n×1,则局部坐标系下,单个径向弹簧单元的节点位移为: (7) 径向弹簧单元的内力,即节点荷载为: (8) 若节点荷载的水平节点力小于等于0,则该径向弹簧单元受拉,应取消;重复式(7)、式(8),对每个径向弹簧单元进行存在性判断。 4)重复1.2.1及1.2.3节步骤,直至无受拉径向弹簧单元存在,此时的[F]3n×1即为合理的初期支护结构所受等效节点荷载矩阵。 1.2.4 确定初期支护结构的结构内力 计算式(4)可得初期支护结构的节点位移[δ]3n×1,在整体坐标系下,梁单元的节点位移为[δ]6×1,则梁单元的节点荷载为: [F1]6×1=[k1]6×6[δ]6×1 (9) 在局部坐标系下,梁单元的节点荷载,即初期支护结构的内力为: (10) 式中[F3]6×1为梁单元自重荷载下的等效节点荷载。 基于上述初期支护变形-结构法的建立流程及步骤,采用MATLAB编写计算程序。MATLAB以矩阵为基本数据单位,其指令表达式与工程及数学中常用的形式十分相似,因此较之其他编程语言,用MATLAB求解问题更加简捷[13-14]。计算程序界面如图3所示,主要包括以下2个方面: 1)读取数据及参数输入。读取数据包括节点坐标及单元节点号,即当梁-弹簧模型建立好后,定义节点坐标及单元点号,分别按梁单元、径向弹簧单元、切向弹簧单元的顺序,将数据存入2个Excel表中,运行程序时,便可以直接读取数据进行计算; 另一部分参数通过编辑框输入,包括弹性模量、梁单元横截面几何参数等。此外,关键节点的位移值也在界面中输入。 2)求解及输出结果。完成第1步的操作后,便可进行“求解”,即可实现变形-结构法结构内力的计算,计算结果会直接在界面右侧部分显示。 图3 程序界面 已知初期支护结构内力,便可依据TB 10003—2016《铁路隧道设计规范》[15](简称《隧规》)中的破损阶段法进行初期支护的安全系数计算,安全系数标准参照《隧规》8.5.2条,初期支护按偏心受压构件计算其安全系数。当初期支护为素混凝土结构时,计算公式及相关参数选取参照《隧规》8.5.5条和8.5.6条;当初期支护为钢筋混凝土结构时,计算公式及相关参数选取参照《隧规》8.5.14条和8.5.15条。具体的初期支护结构安全性评价流程如图4所示。 依据《隧规》分别计算隧道浅埋及深埋情况下的围岩压力,运用荷载-结构法求得初期支护结构内力及节点位移。之后采用MATLAB对初期支护节点号进行随机抽样,分别选取5~11个节点为关键节点。需要指出的是,隧道监控量测时,拱顶点为必测点,且水平收敛采用水平测线进行量测,因此关键节点选取时,拱顶点必选,两侧边墙则选取平行的成对节点,这样既满足工程实际,又可极大地提高随机抽样的效率。之后,采用变形-结构法求得结构内力,并与荷载-结构法计算结果进行结构内力及安全系数的比较,从而确定关键节点的合理空间位置分布及数量。 图4 初期支护结构安全性评价流程 浅埋竖向及侧向围岩压力: (11) (12) (13) ei=γhiλ (14) 式(11)—(14)中:q浅为浅埋竖向围岩压力,kN;γ为围岩重度,kN/m3;h为洞顶离地面的高度,m;θ为顶板土柱两侧摩擦角,(°);B为坑道跨度,m;λ为侧压力系数;φc为围岩计算摩擦角,(°);β为产生最大推力时的破裂角,(°);ei为浅埋隧道不同位置水平围岩压力,kN;hi为内外侧任意点至地面的距离,m。 深埋竖向及侧向围岩压力: q深=γh (15) h=0.45×2s-1[1+i(B-5)] (16) e=λq深 (17) 式(15)—(17)中:q深为深埋竖向围岩压力,kN;s为围岩级别;i为每增减1 m时的围岩压力增减率;e为深埋水平围岩压力,kN。 以时速350 km高速铁路双线隧道Ⅳ级浅埋(17 m)及深埋围岩为例,隧道开挖高度为12.23 m,开挖跨度为14.70 m,隧道断面如图5所示。初期支护划分为44个1.0 m单元和节点,计算素混凝土及配筋情况下,隧道初期支护结构内力和安全系数。初期支护建筑材料选用C30喷混凝土、HRB400钢筋,围岩及建筑材料参数按《隧规》选取。计算工况见表1。 图5 隧道断面图(单位: cm) 3.3.1 关键节点的合理空间位置分布确定 通过大量计算可知,关键节点的空间位置分布越集中,变形-结构法求解的结构内力及安全系数的相对误差越大,即关键节点的空间位置应尽可能均布; 且关键节点在空间位置均布情况基本相同的条件下,应兼顾特征点,如拱顶点、跨度最大点、墙脚点等的工况,变形-结构法求解的结构内力及安全系数的相对误差最小。关键节点的合理空间位置分布如图6所示。 图6 关键节点位置分布 3.3.2 关键节点的合理数量确定 在关键节点空间位置分布合理的前提下,确定关键节点的合理数量,以深埋钢筋混凝土初期支护结构为例。计算得到结构的内力情况如图7和图8所示,结构的安全系数如图9所示。 图7 单元轴力变化曲线 图8 单元弯矩变化曲线 图9 单元安全系数变化曲线 由图7—9可知,基于变形-结构法求解的结构内力及安全系数均随着关键节点数量的增加而逐渐逼近荷载-结构法的结果,结构内力及安全系数的相对误差逐渐减小,各单元内力及截面安全系数的大小分布形式也逐渐趋于一致。其他工况计算结果规律也完全一致。 在进行隧道支护结构设计时,往往以最不利截面,即安全系数最小的单元截面作为控制截面。各工况下控制截面(31号单元)的安全系数及其相对误差,以及各单元截面安全系数相对误差的最大值见表2。 表2 支护结构安全系数相对误差 由表2可知,当关键节点数量大于等于7时,基于变形-结构法求解的结构最大安全系数相对误差均在10%以内,计算精度较高; 当关键节点数量大于等于5时,基于变形-结构法求解的结构最不利截面位置与荷载-结构法的结果一致,最不利截面安全系数的相对误差,对于素混凝土支护结构约为10%,对于钢筋混凝土支护结构约为5%,计算精度较高。考虑到现行隧道设计中,常规隧道设计断面尺寸均不超过上述断面,即进行变形-结构法计算时,关键节点的占比将会高于上述情况,因此支护结构内力及安全系数的相对误差将会进一步缩小。基于此,可确定关键节点的数量应大于等于5。考虑到施工现场的复杂性,为保证结果的准确性,建议关键节点的数量取7。 香炉坪隧道位于湖北省兴山县境内,为新建郑州至万州高速铁路湖北段控制性工程之一。属于时速350 km的高速铁路双线隧道,隧道采用大型机械化配套全断面工法施工,全长15 145 m,最大埋深1 100 m。隧址区位于秦岭大巴山体系,总体上属于侵蚀中低山沟谷地貌,地形波状起伏,山高坡陡,沟谷区域地形相对较缓,多呈“V”字型沟谷。高差较大,地面高程386~1 670 m,自然横坡30°~50°,局部较缓形成台地。隧址区上覆第四系全新统冲洪积(Q4al+pl)及坡洪积(Q4dl+pl)卵石土,坡崩积层(Q4dl+col)碎石土、滑坡堆积层(Q4del)碎石土和坡残积(Q4dl+el)粉质黏土为主; 下伏基岩为侏罗系中统下沙溪庙组(J2xs)砂岩、泥岩互层夹页岩,中下统聂家山组(J1-2n)粉砂岩夹泥岩,下统珍珠冲组(J1z)粉砂岩夹泥岩夹页岩、页岩夹薄煤层; 三叠系上统须家河组(T3xj)砂岩夹页岩、炭质页岩夹煤。 选取香炉坪隧道2#斜井D1K597+44为测试断面,测试断面为Ⅳ级围岩。在测试断面布置9个关键节点(见图10),采用全站仪分别测量记录各关键节点的竖向变形值和水平变形值,直至稳定。隧道开挖后,由于初测的滞后性,初期支护初测前一段时间内的变形难以准确测得,从而影响了计算结果的准确性,因此应尽早开始初测。由于本测试断面关键节点布置于初期支护施作时,初测于初期支护喷混完毕,时间间隔较短,近似认为所测变形值为初期支护真实变形值,各关键节点的累计位移值见表3。 图10 关键节点布置示意图 关键点竖向变形累计值/mm水平变形累计值/mmA-26.70.0B-13.6-3.2C-12.44.1D-8.3-7.4E-7.68.0F-8.2-3.1G-8.13.3H-7.6-0.9I-6.61.2 依据设计,测试断面初期支护采用C30喷射混凝土,Ⅰ18型钢钢架,钢架间距1 m,初期支护厚度为25 mm; 建筑材料参数按《隧规》选取。围岩径向弹性反力系数由Callerkin计算公式确定,即k=E/(1+μ)r0=100 MPa/m,其中岩体变形模量E取1.1 GPa; 泊松比μ取0.4; 由于高铁隧道断面为非圆形,因此采用开挖断面的最小外接圆作为拟合断面,取其半径为隧道近似半径,即r0=7.4 m; 围岩切向弹性反力系数取径向弹性反力系数的1/2[16]。计算得到初期支护的安全系数变化曲线如图11所示。 图11 测试断面初期支护的安全系数变化曲线 Fig. 11 Variation curve of safety factor of primary support of test section 《隧规》中对于钢筋混凝土结构,截面受压破坏时安全系数取2.0,受拉破坏时安全系数取2.4。由图10可知,初期支护各单元截面安全系数均大于规范值,表明其处于安全状态,这与现场的实际情况吻合,一定程度上表明了本文方法的合理性。 本文基于矩阵位移法,建立了以关键节点位移为已知量的变形-结构法,即由关键节点的位移值直接反算结构荷载及内力,进而依据规范定量评价初期支护的安全性;并编制了相应的计算程序,依托郑万高铁香炉坪隧道进行了工程应用分析。得到结论如下。 1)变形-结构法较之其他以位移为基础的反分析方法,具有原理简单、参数易选取、计算速度快的优点。 2)变形-结构法中,关键节点的空间位置应尽可能均布,且应兼顾特征点,如拱顶点、跨度最大点、墙脚点等,且关键节点的数量应大于等于5。考虑到施工现场的复杂性,为保证结果的准确性,建议关键节点的数量取7。 3)由基于变形-结构法的初期支护安全性评价方法的工程应用分析可知,安全性评价结果与现场的实际情况吻合。隧道施工过程中,可通过关键节点的位移监控量测数据,利用变形-结构法进行初期支护的安全性评价。 4)围岩弹性反力系数的大小对初期支护结构的内力影响较大,不同隧道工程围岩弹性反力系数往往不一样。因此,为提高变形-结构法的准确性,进一步研究围岩弹性反力系数的合理确定方法是必要的。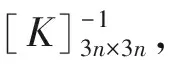
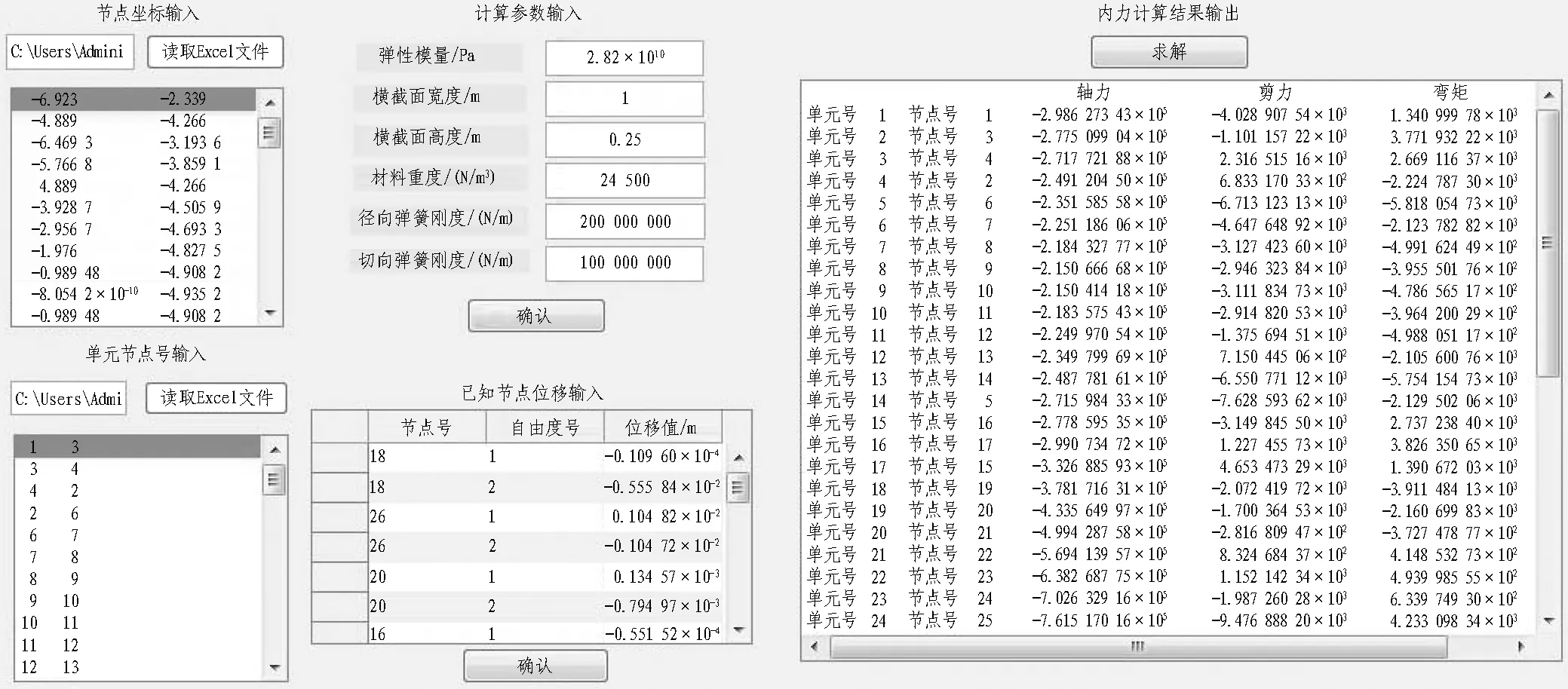
1.3 变形-结构法程序设计
2 初期支护结构安全性评价
3 关键节点选取
3.1 选取方法


3.2 计算工况及参数

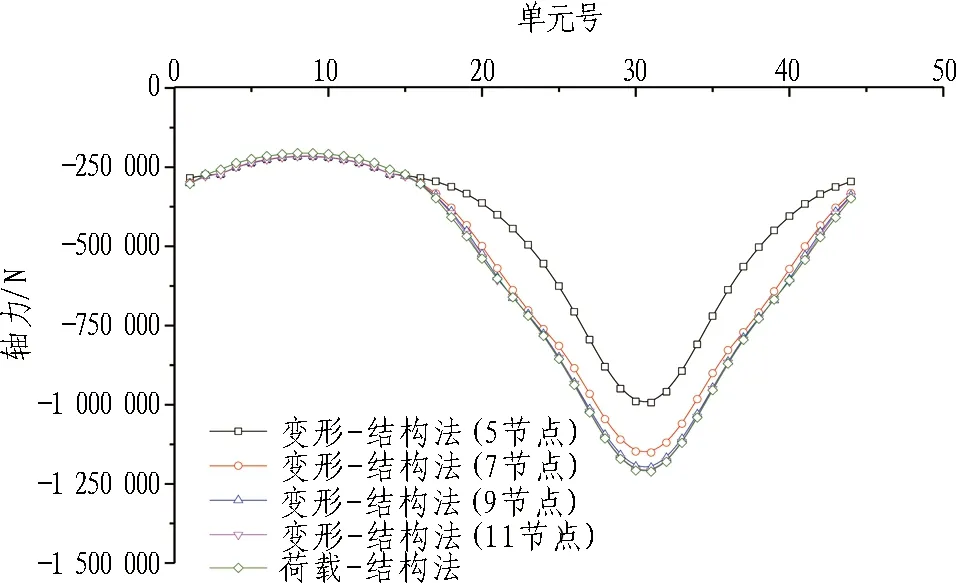
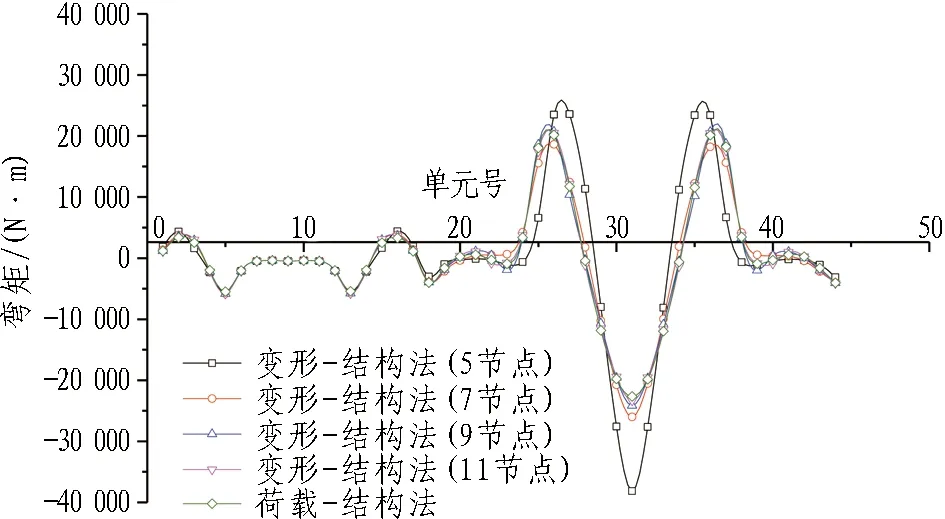
3.3 计算结果及分析


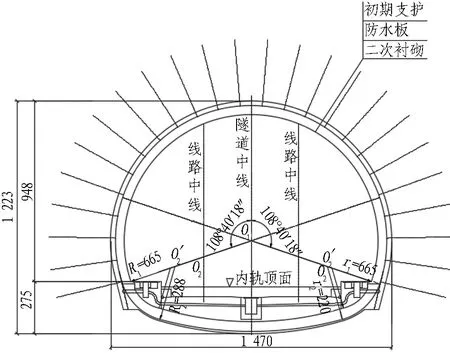
4 工程应用分析
4.1 工程概况
4.2 断面安全性评价


5 结论与讨论
