基于DGPS-SINS组合导航系统的定日镜清洗机器人设计

■徐能 宓霄凌＊ 张旭中 胡玉超 陈康立 薛刚强 熊步青

(1.浙江中控太阳能技术有限公司；2.青海中控太阳能发电有限公司)

0 引言

定日镜作为塔式太阳能热发电站中聚光集热系统的核心部件，其光学效率会直接影响整个电站的性能。由于定日镜在户外环境运行，空气中的粉尘及其他污染物等逐渐在其表面堆积，使其表面的光学反射率下降。因此，必须设计高效的定日镜清洗方式，对定日镜进行周期性清洗，以提升整个电站的发电效率。

目前，针对世界范围内已投运的塔式太阳能热发电站的定日镜清洗方式，有大量的研究和试验。Sener公司和Torresol Energy公司针对西班牙已投运的19.9 MW Gemasolar塔式热发电站联合开发了一款智能清洗机器人[1]，该机器人被放置在水平镜面上，可自动行走完成清扫。美国Bright Source公司针对其2014年2月投运的392 MW Ivanpah塔式热发电站设计了一款基于GPS定位的自动清洗车[2]，清洗车本体为一台起重机，清洗刷辊通过一根长24.5m的可伸缩机械臂固定在本体上，在同一个位置可清洗约24.5m范围内的定日镜，并可通过增加机械臂长度来减少清洗车在镜场内的行进里程。美国2015年3月投运的新月沙丘110MW塔式热发电站采用的清洗车是通过在重型车辆本体上搭载水箱的方式，由人工操纵清洗定日镜。

虽然上述清洗方式在清洗单个镜面时可实现自动清洗，但在整个镜场的清洗过程中仍需要人工干预，如人工控制机械臂的位置、控制执行机构的姿态、移动清洗车位置等。这样既增加了运维成本，又使在清洗过程中待清洗的定日镜必须由正常运行状态切换至清洗状态，导致这部分定日镜无法用于“追日”，影响了镜场的可利用率。

基于上述分析，浙江中控太阳能技术有限公司以中控德令哈50MW塔式太阳能热发电站为背景，设计了一款全自主执行清洗任务的机器人，可用于塔式太阳能热发电站定日镜的清洗，结构如图1所示。该清洗机器人通过在本体上搭载清洗水箱，并结合高压喷嘴、刷辊及精密的距离传感器控制执行机构主动靠近镜面，以完成清洗任务。

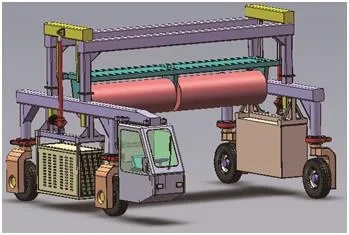
图1 定日镜清洗机器人结构图

由于该清洗机器人的行进和清洗任务均是在无人工干预的情况下自主完成的，因此可将清洗任务安排在镜场关场后的非日间时段。这样做避免了日间清洗时定日镜处于待清洗状态而造成的能量损失，有效提高了镜场的运营效率，降低了运维成本。

移动机器人的自主导航方式一般包括GPS导航、惯性导航(INS)、激光雷达导航[3-9]等。GPS导航具有全球性、全天候、高精度和三维定位等优点，但也存在数据易丢失、可靠性差等缺点；INS完全依靠载体自身设备独立导航；不与外界发生联系，数据不易受到干扰，但是INS的误差会随着时间累积，不适合长距离导航。所以将两者进行融合，可有效提高导航的精度和可靠性。然而在机器人行进过程中，不可避免地会出现GPS-INS信息丢失、行进轨迹发生偏移等情况，此时需要机器人具备感知周围局部环境的能力，激光雷达导航因测量精度高、数据量小、不受环境中光线影响等优点，在机器人局部环境感知领域得到了广泛应用[6]。

基于上述分析，结合清洗机器人需具备高精度运行轨迹的要求，本文拟采用差分全球定位系统(Differential Global Positioning System，DGPS)与捷联惯性导航系统(Strapdown Inertial Navigation System，SINS)相组合的导航方式，以获得机器人cm级的定位精度。同时，结合二维激光雷达完成障碍物检测，并充分利用镜场运行环境特性，开发了基于定日镜立柱识别的同时定位和建图(Simultaneous localization and mapping,SLAM)[7-10]，对机器人清洗过程中的路径进行优化，降低了因DGPS-SNIS故障或漂移导致清洗机器人与定日镜发生碰撞的风险。该清洗机器人在行进过程中，结合红外相机、可见光相机等测量单元，对定日镜相对机器人的姿态进行识别，完成镜面防碰撞检测，确保自主执行任务期间的稳定性和安全性。

本文主要针对定日镜清洗机器人的组合导航系统进行设计和验证。首先，建立了机器人系统地面导航系统坐标系，给出了WGS-84坐标系至当地导航系统坐标系的转换方程；其次，建立了基于扩展卡尔曼滤波(Extended Kalman Filer，EKF)算法的机器人导航方程；然后，介绍了二维激光雷达测量原理，对点云数据聚类算法进行了设计和测试，同时根据聚类结果对立柱特征进行模板匹配，基于对立柱的观测信息研究了清洗机器人即时定位与地图构建(SLAM)算法；最后，基于模型样车对设计的导航系统在模拟镜场环境下进行测试验证。

1 地面导航系统坐标系(ENU)

由于GPS广播星历采用WGS-84坐标系，其输出为测点的经度B、纬度L和高度H信息，不利于地面导航系统方程的建立，因此需要将其转换至地面导航系统坐标系ON-ENU下。该坐标系原点为地面上1个已知精确经度、纬度、高度信息的测站点ON；ONN轴为过点ON的子午线切线，指向正北方向；ONE轴为过点ON的椭球平行圈切线，指向正东方向；ONU由ONE、ONN根据右手定则确定，指向天顶方向。具体如图2所示。

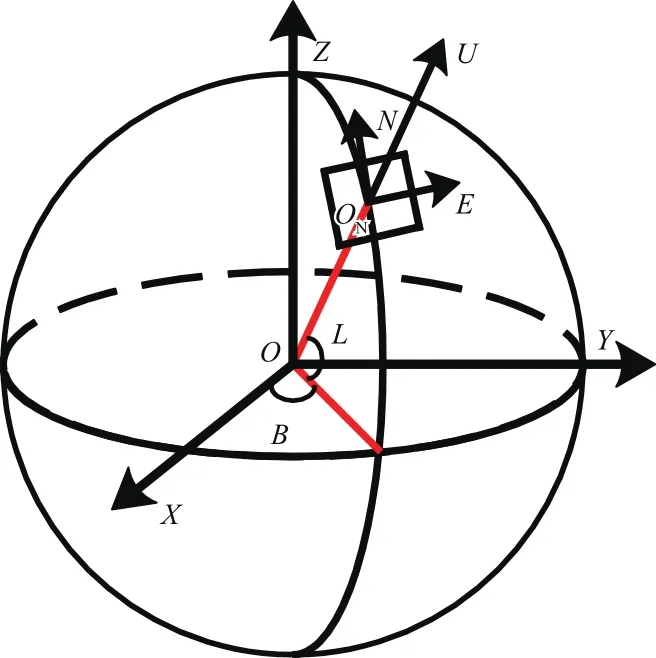
图2 地面导航系统坐标系

将WGS-84坐标系转换到地面导航系统坐标系，需要将基准站ON的经度、纬度和高度信息()B,L,H转换至O-XYZ直角坐标系下，即：

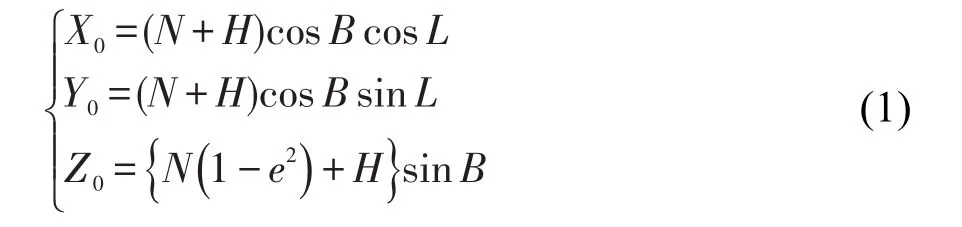
式中，e为WGS-84坐标系椭球对应的第一偏心率；N为纬度L处卯酉圈曲率半径。

式中，a、b分别为WGS-84坐标系椭球对应的长半轴、短半轴。

在机器人实时测量时，将获取的WGS-84坐标系下的经度、纬度、高度坐标(Bm,Lm,Hm)按照式(1)计算得到其空间直角坐标为(Xm,Ym,Zm)。

移动站和基站间的相对坐标[ΔX,ΔY,ΔZ]T为：

式中，T为转置。

则移动站在地面导航系统坐标系下的坐标由式(5)确定[11]：

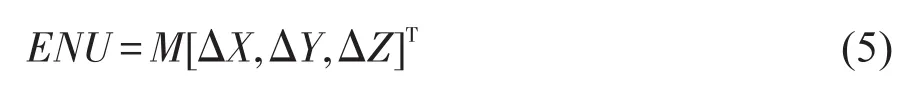
式中，

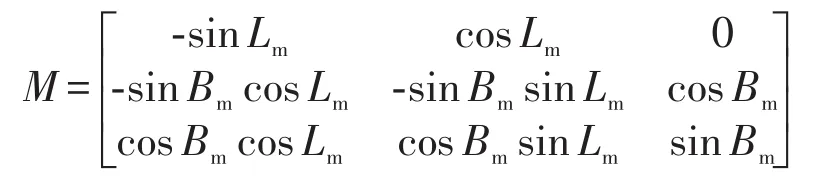
DGPS-SINS差分定位定向时，通过解析包含有UTC时间、速率、航向角等数据的$GPFPD报文，按照式(1)将与机器人运行相关的状态信息转换至地面导航系统坐标系下，以进行清洗机器人系统的导航与控制。

2 扩展卡尔曼滤波(EKF)方程

全局坐标系下机器人位姿如图3所示，图中L1、C、Po、Φ分别为机器人轮基长度、参考控制点、质心与前轮的偏角。机器人采用后轮驱动前轮转向的结构，其运动学方程满足Ackerman转向几何约束[12]。DGPS-SNIS系统在运动过程中，由于受路面颠簸、发动机震动等干扰因素的影响，会出现噪声及野值，使获取的位姿数据受到干扰，进而影响机器人的控制。考虑到机器人运动方程的非线性特性，本文采用EKF算法对机器人状态数据进行滤波。由于机器人系统在地面上运动，所以这里暂不考虑其在高度方向的状态变化。

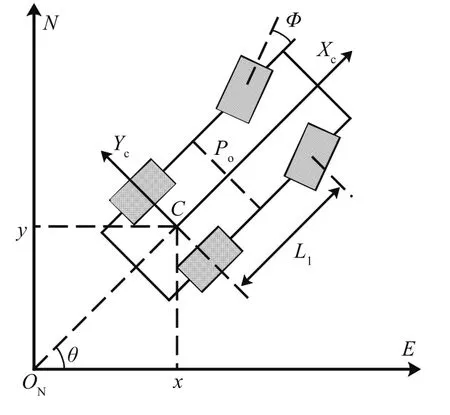
图3 全局坐标系下机器人位姿

机器人系统运动学模型可表示为[13]：

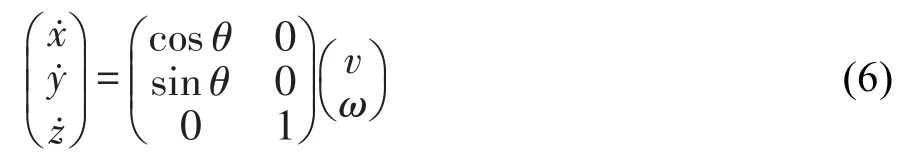
式中，v、ω分别为机器人运行的速度、本体转动角速度[13-14]；为机器人在参考点C的速度在地面导航系统坐标系下的分量；θ为车体航向角。

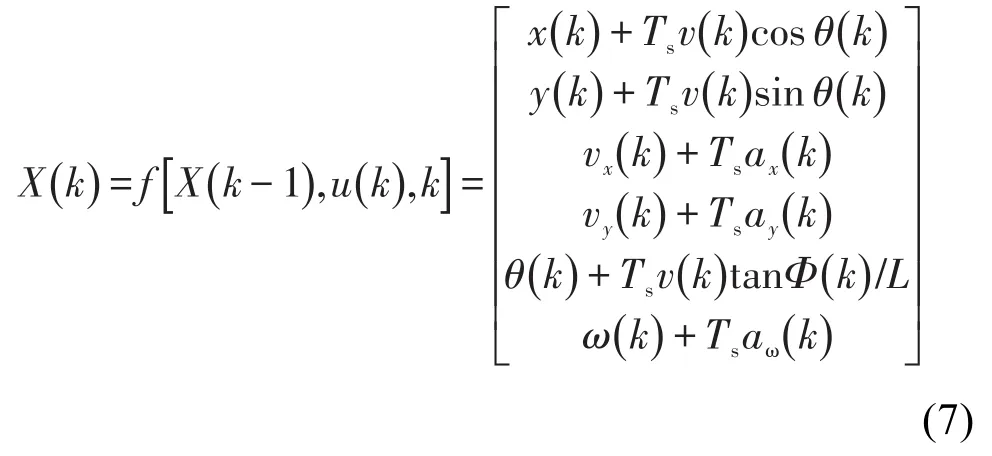
式中，为车体航向角速度；Ts为采样周期；aω为角加速度；k为时刻；ax为x方向的加速度；ay为y方向的加速度。

设系统噪声W为白噪声，则式(7)可表示为普遍状态方程的形式，即：

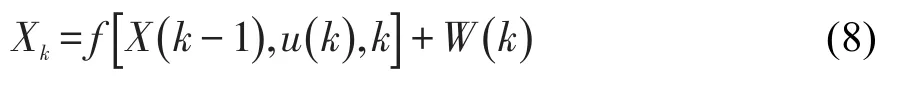
式中，Xk为第k时刻计算的X值。

式(8)为非线性方程，在当前状态处Taylor公式展开进行线性化处理，得到系统的Jacobian矩阵，可表示为：

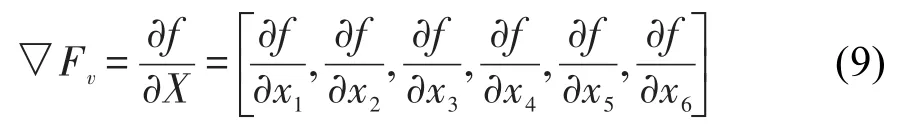
式中，Fv为X的偏导数。

系统观测方程为：

式中，Zk为k时刻的测量值(观测值)，是滤波的输入为状态变量到测量(观测)的转换矩阵，H1=[I5×505×1]，其中I为单位矩阵；Vk为观测噪声。

Kalman滤波方程式[15]为：

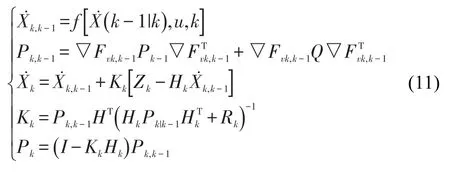
初始时刻给定状态和误差矩阵初值与P0，结合滤波方程式(11)在k-1时刻的状态预测值为,k-1，通过测量值Zk对预测值修正即可获得状态估值。

3 机器人SLAM算法

3.1 激光雷达测量模型

单线激光雷达测量原理如图4所示。

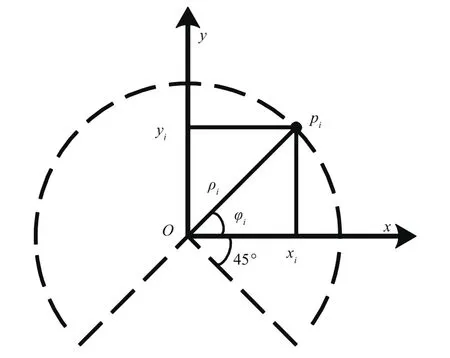
图4 激光雷达测量模型

图4中，ρi为第i个测点pi到测量探头的距离；φi为pi与x轴方向的夹角。单线激光雷达的扫描角度范围为-45°～225°，扫描角分辨率Δφ=0.25°，完成一次扫描共返回1081个以极坐标(ρi,φi)形式表示的数据点。

本文采用基于密度分布的聚类(Density-based spatialclusteringofapplicationswithnoise，DBSCAN)算法[16-17]，对激光雷达测量的原始数据进行聚类，并进行识别和模板匹配，基本的模板包括基于圆形轮廓辨识的圆柱形目标、基于直线识别[18]的规则目标物和其他不规则物体，以区分出立柱和障碍物。由于在镜场建设时已获得全镜场立柱的精确坐标，所以对立柱的识别可用于机器人局部环境定位和建图；对障碍物进行识别用于机器人防撞。图5为试验环境下对随机设置的不同形状的物体聚类测试结果，其中白色“o”为原始数据中的测量噪点，不同颜色类代表扫描范围内不同的物体。该算法能对目标物有效聚类，并滤除测量到的噪声。因此，可根据扫描的立柱信息，获得目标相对于机器人的位置和方位。

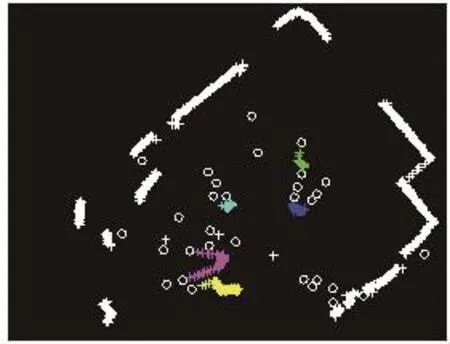
图5 试验环境下对随机设置的不同形状的物体激光雷达数据聚类结果

3.2 EKF-SLAM算法

镜场SLAM问题的基本场景如图6所示：清洗机器人在镜场内清洗，通过DGPS-SINS获得自己的全局位姿，同时利用测到的立柱信息递增的建立机器人导航地图，完成机器人即时建图和定位，对机器人运行轨迹进行优化确认。

行进过程中，由运动学方程可将机器人位姿xv,k表示为：

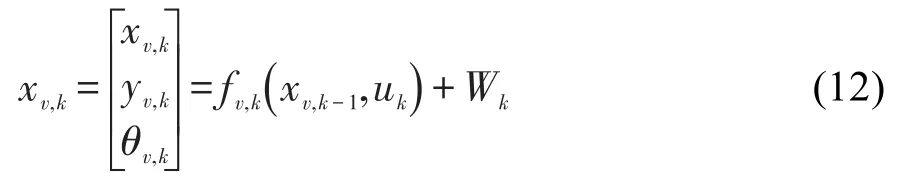
式中，xv,k、yv,k分别为k时刻x方向、y方向的速度；Qv,k为k时刻的航向角；Wk为零均值，协方差为Qk的高斯白噪声。

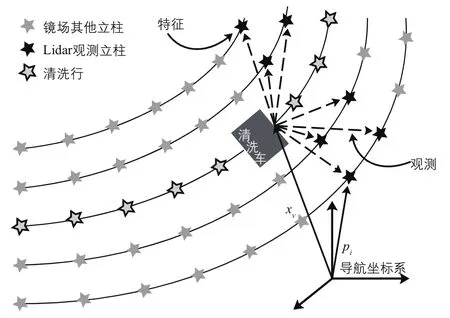
图6 镜场SLAM场景示意图

将第fi个立柱在机器人移动过程中的观测向量Zk的方程可表示为距离ρi和方位φi的形式，即：

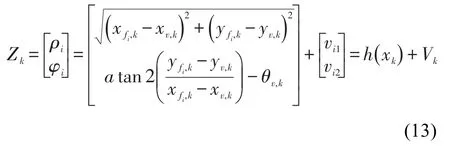
式中，Vk为零均值，协方差为Rk的高斯白噪声；对应的转换矩阵。

本节基于式(11)的EKF基本框架推导机器人的SLAM算法。根据机器人运动时序，将SLAM算法分成预测、观测、更新和增广4个阶段。

预测阶段需要在车辆运动后更新系统状态向量和协方差矩阵。

系统协方差矩阵Pk可表示为：

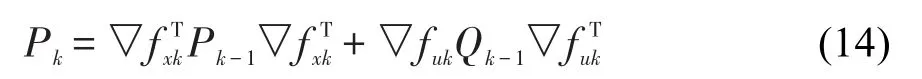
系统协方差矩阵Pk还可表示为：

式中，Pvv为机器人位姿协方差矩阵；Pvm为机器人和立柱的互协方差矩阵，且有Pmm为立柱协方差矩阵。

观测阶段通过激光雷达扫描获取立柱的状态信息，观测向量的预测值线性化后形成式(16)：

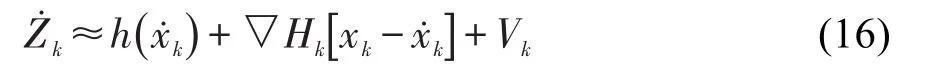
式中，▽Hk为观测方程的Jacobian矩阵。

协方差矩阵Pzz,k可表示为：

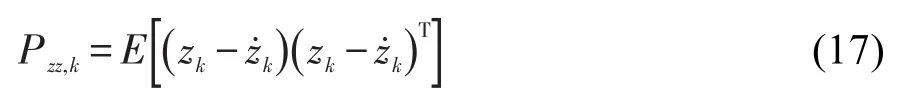
式(17)展开后可简化为：

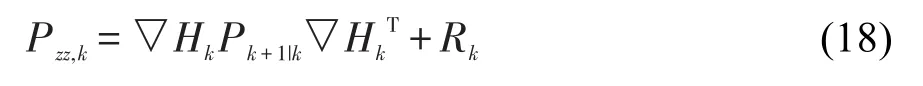
式中，Pk+1|k为根据k时刻的Pk值及系统模型预测的第k+1时刻的P值。

▽Hk可表示为：

针对第1根观测到的立柱，则有：

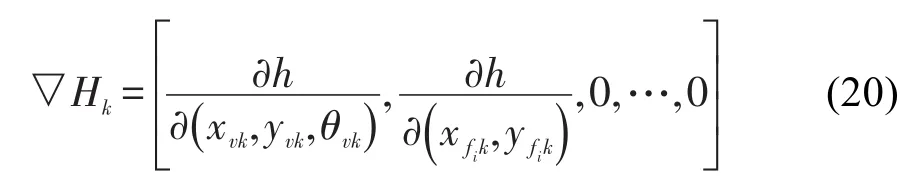
对第2根观测到的立柱，则有：

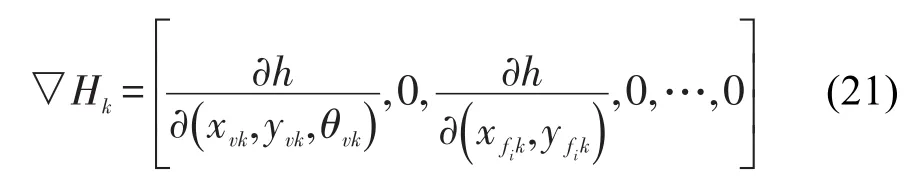
其他情况以此类推。

下一步利用预测值和观测值来更新系统的状态向量和协方差矩阵，具体的步骤为式(22)～式(24)：

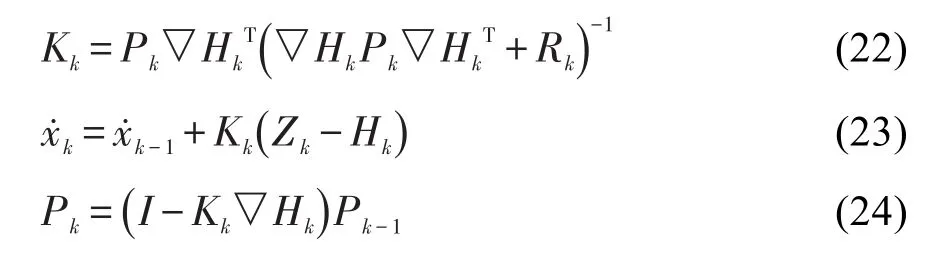
新状态向量的协方差矩阵为：

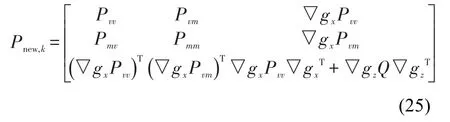
式中，▽gx，▽gz分别为g对xv,k和zj,k的Jacobian矩阵。

清洗机器人现场运行时，通过传感器不断测量，将新观测到的立柱向量加入到联合状态向量，并对清洗机器人估计的位置进行更新，完成清洗机器人局部环境定位和建图，对清洗机器人局部运行轨迹进行修正优化，降低清洗机器人与定日镜碰撞的风险。

由于机器人执行清洗任务的清洗行有几百甚至上千个被扫描的“路标”立柱，随着移动机器人观测路标的增多，系统状态向量的维数不断增加，协方差矩阵和Jacobian矩阵的计算量急剧加大，从而导致算法运行的效率和定位精度[19]降低，因此本方案采用以DGPS-SINS导航为主，以基于激光雷达的机器人SLAM导航为辅的组合导航方式，有效完成清洗机器人全局和局部环境下的自主导航，提高了系统的精度、稳定性和容错鲁棒性。

4 仿真测试及分析

对设计的组合导航算法进行了基于模型机器人的圆形轨迹跟踪测试，并对基于激光雷达的SLAM算法进行了仿真验证。

模型机器人基本参数为轮基长度L1=1.02 m，GPS帧率为20Hz，控制周期为0.1s，机器人名义线速度vn=0.4m/s，圆形轨迹半径R=7.48m，测试结果如图7～图11所示。

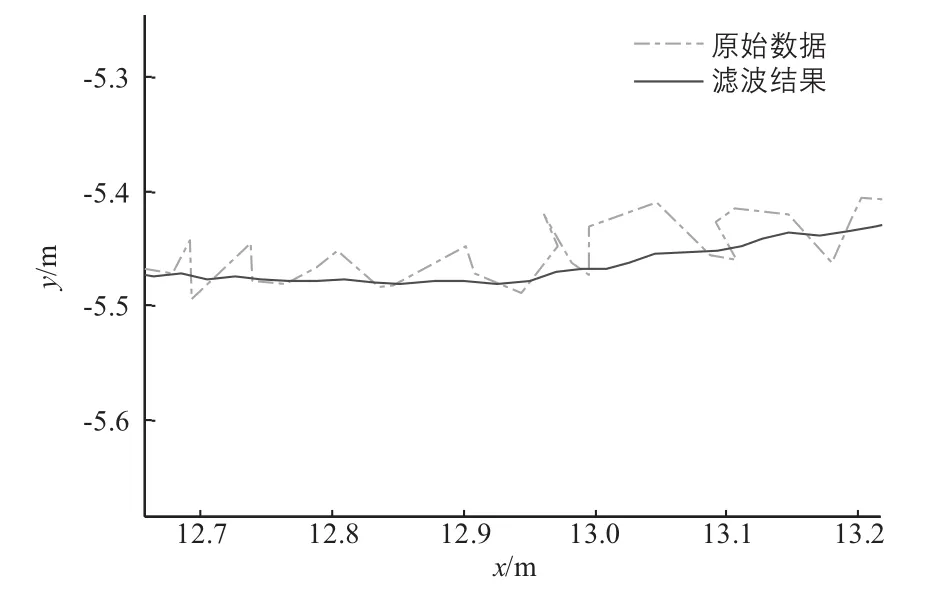
图7 圆形轨迹局部放大图

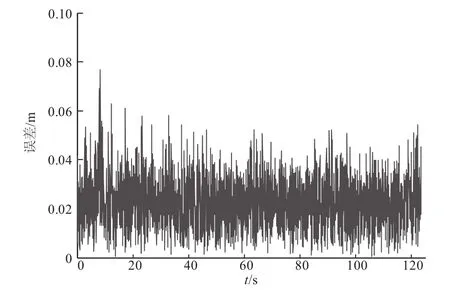
图8 Kalman滤波误差

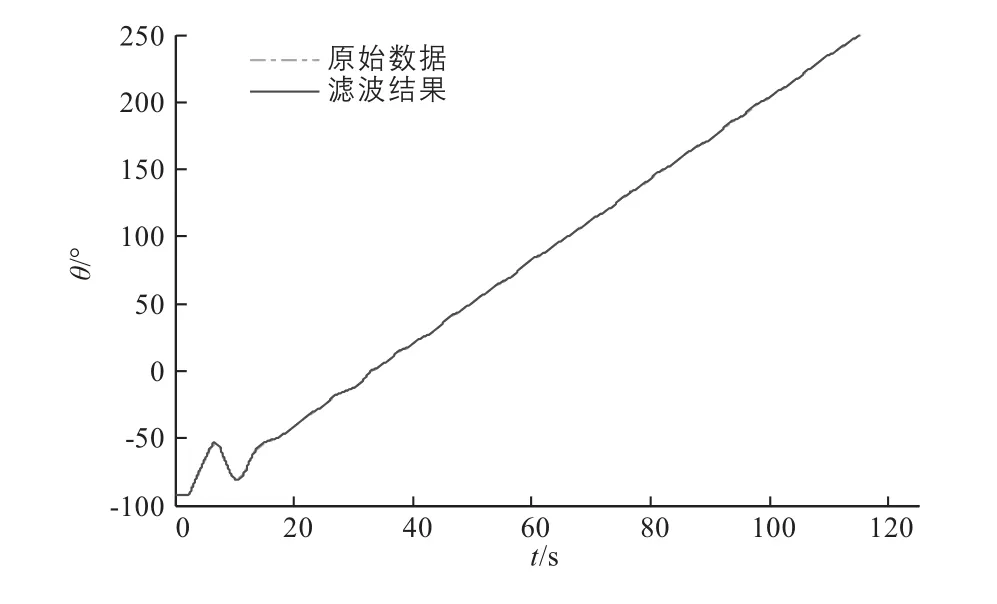
图9 车体航向角θ跟踪曲线

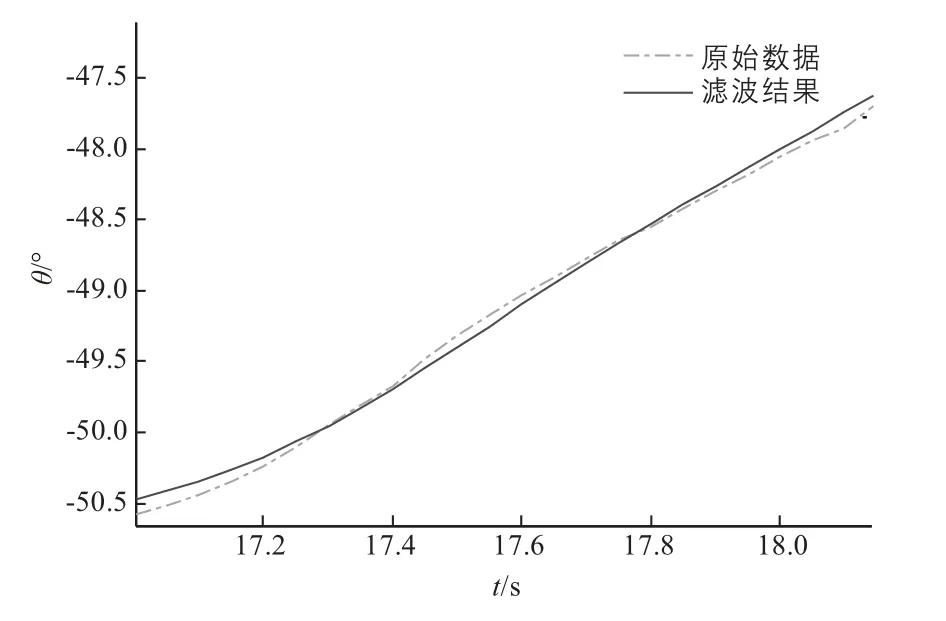
图10 车体航向角θ跟踪曲线局部放大图

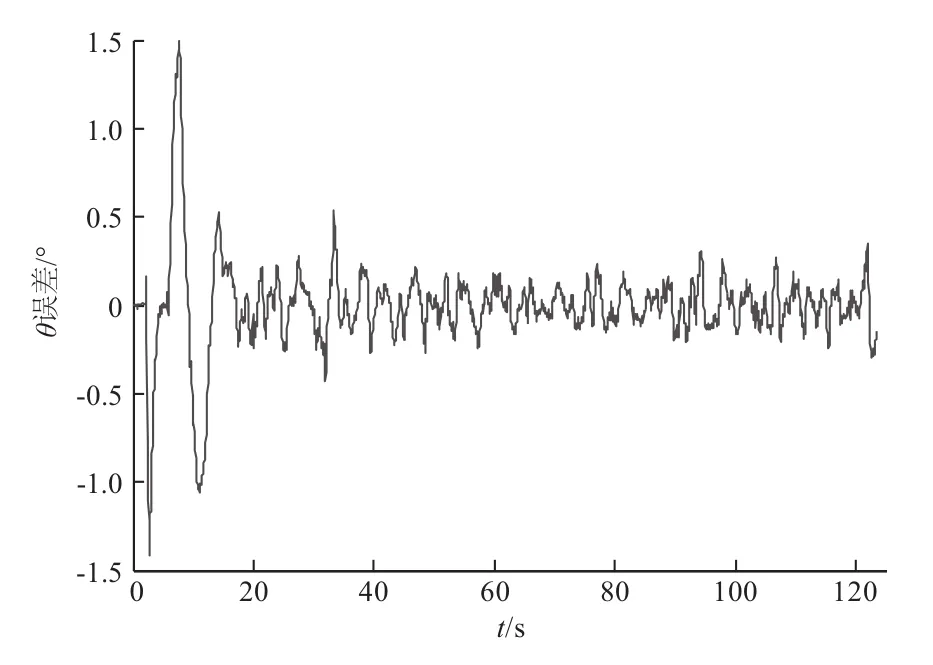
图11 车体航向角θ跟踪误差曲线

从图7和图10可以看出，算法对设备输出的具有剧烈抖动特性的原始数据进行了有效地滤波和平滑，保证了机器人导航和控制系统的精度和稳定性。在实际测试过程中也发现，这种高频抖动的原始数据也会给控制执行机构带来剧烈抖动，会严重影响控制执行机构的安全性能，设计的滤波算法有效地解决了上述问题。

仿真开始前约15s内，机器人位于圆形轨迹外任意一点并处于静止的预备状态。15s以后，机器人开始进行轨迹跟踪，测试结果表明，Kalman滤波器对机器人位置的估计误差均值为0.023m，对航向角估计误差均值为0.0043°。由于模型机器人GPS天线基线长度与机器人轮基长度均为1.02 m，所以机器人在静止状态下，前后天线的定位波动会导致约±1.5°的航向角计算误差；一旦机器人处于移动状态，该误差会降低且趋于稳定(如图11所示)。而实际的清洗机器人轮基长度约为2m，因此估计的航向角精度将优于此次测试的情况。

基于二维激光雷达的清洗机器人SLAM算法仿真测试结果如图12所示。清洗机器人在行进过程中，不断扫描获取清洗机器人周围的立柱信息并完成对立柱的匹配；进而结合该观测量对清洗机器人进行局部环境下的定位和建图，有效降低了系统的运行风险。

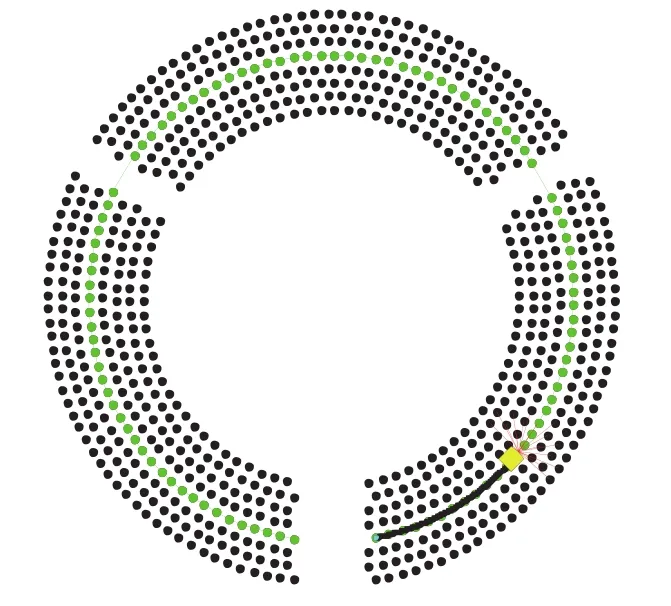
图12 清洗机器人SLAM路径导航结果

5 结论

针对现有塔式太阳能热发电站定日镜清洗方案存在的运维成本高、影响镜场利用率、人工干预清洗效率低等突出问题，本文设计了一款全自主清洗机器人，重点设计了基于DGPS-SINS组合导航系统的机器人，同时针对机器人导航系统设计了EKF算法，对系统状态进行滤波和最优估计，有效提高了导航系统的精度和稳定性；并结合太阳能热发电站定日镜布局特性和机器人运行环境特点，提出了采用二维激光雷达实现机器人SLAM算法，通过多传感器融合方案，优化了机器人清洗过程中的位置精度，降低了机器人本体与镜面碰撞的风险。最后，对设计的方案进行了样机测试仿真验证，结果表明，设计的方案和算法能够满足镜场环境下清洗机器人的运行需求。