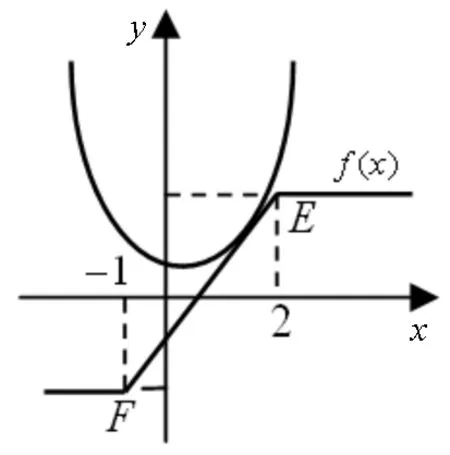
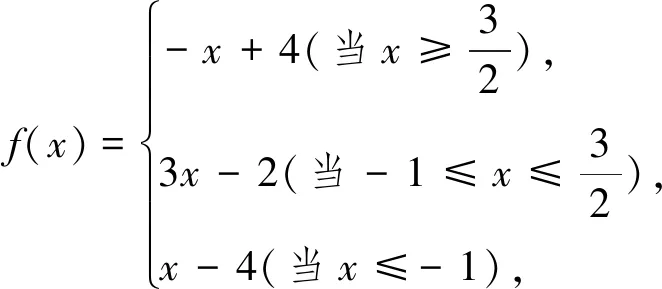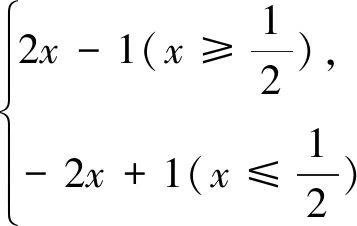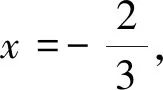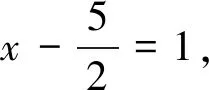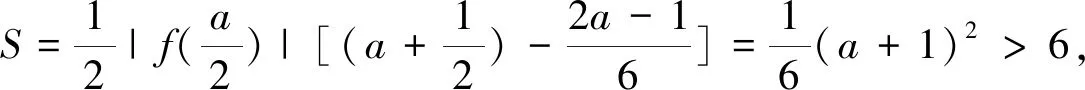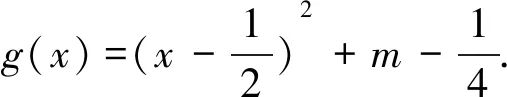基于直观想象下的不等式选做题解法探究 *
2019-10-14广东省封开县江口中学526500黎伟初
广东省封开县江口中学 (526500) 黎伟初
直观想象是指借助几何直观和空间想象感知事物的形态和变化,利用图形理解和解决数学问题的过程.探究图形解决不等式选做题,以培养学生的创新思维.高考题中的不等式选做题,通常是以与两个绝对值之和(差)或一个绝对值等有关联来命制,常见的题型有:①求不等式解集;②依恒成立、能成立(有解)、无解等条件,求出参数的取值范围;③涉及到不等式证明等.含一个绝对值或两个绝对值之和(差)的不等式的解法有多种,本文着重研究:通过构造函数图象的手段来处理(来自教材的构造函数法).含两个绝对值之和(差)或一个绝对值的函数,形如f(x)=|ax+b|±|cx+d|与f(x)=|ax+b|的函数图象是有规律的,总结得到十种图式,分别为:①∨形图;②平底桶形;③斜底桶形(两种);④左右游泳形(两种);⑤开口向上鸟形(两种);⑥开口向下鸟形(两种).熟悉这十种图式,铭记于心,作图时就能驾轻就熟,有章可循!
一、含一个绝对值的情形

图1
形如f(x)=|ax+b|(其中a>0)的函数,其图象为图1:
图式:∨形图;左右两条射线交于x轴上同一个点
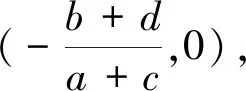

二、含两个绝对值之和(差)的情形
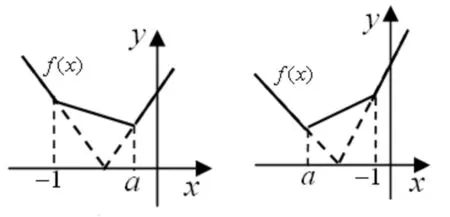
形如f(x)=|ax+b|±|cx+d|(其中a>0,c>0)的函数,其图象共有九种图式:

图2
1.可化为形如f(x)=|ax+b|+|cx+d|(其中a>0,c>0)的函数,当a=c且b≠d时,其图象为图2:


图3
2.可化为形如f(x)=|ax+b|+|cx+d|(其中a>0,c>0)的函数,当a≠c时,其图象为图3:

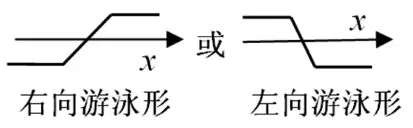
图4
3.可化为形如f(x)=
|ax+b|-|cx+d|(其中a>0,c>0)的函数,当a=c且b≠d,其图象为图4:

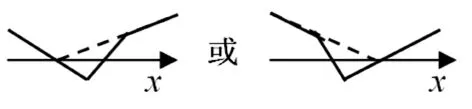
图5
4.可化为形如
f
(
x
)=|
ax
+
b
|-|
cx
+
d
|(其中
a
>0,
c
>0)的函数,当
a
>
c
时,其图象为图5:


图6
5.可化为形如
f
(
x
)=|
ax
+
b
|-|
cx
+
d
|(其中
a
>0,
c
>0)的函数,当
a
<
c
时,其图象为图6:

三、图象法解题的操作流程
第一步:根据个人认知需要处理不等式两边,并确定是否需要合理地移项.可能的话可把含绝对值的项归在左边,其它的项归在右边;也可以把含自变量的项通通归在左边,常数项归右边.
第二步:两边构造函数,并作出两边函数图象.题目两边的不等关系转化为两个函数图象的高低关系去审视,依据求解目标解决相关问题.
四、图象直观性解题的实例观赏
例1 (2013年全国卷Ⅰ)已知f(x)=|2x-
1|+|2x+a|,g(x)=x+3.①当a=-2时,求不等式f(x)


图7
解:①当a=-2时,f(x)=|2x-1|+|2x-2|,即f(x)=
如图7,令4x-3=x+3,得x=2;令-4x+3=x+3,得x=0,结合图象得f(x) 图8 简评:第②问若用纯代数推理会有难度;若借助“平底桶形”图便能直观地分辨f(x)与g(x)的单调性,以及大小与高低的关系,快速破解题目所蕴含的意蕴,达到釜底抽薪,化难为易之功效,彰显了以图助数的魅力所在. 图9 ②分三类讨论: (ⅰ)当a=-1时,f(x)=3|x+1|≥0,f(x)最小值为0,不合题意. (ⅱ)当a>-1时, 图10 图11 如图10,f(x)最小值在x=a处取得,所以 f(x)min=f(a)=a+1=5,即a=4,又因为a>-1,所以a=4吻合; (ⅲ)当a<-1时, 如图11,f(x)最小值在x=a处取得,所以 f(x)min=f(a)=-a-1=5,即a=-6,又因为a<-1,所以a=-6吻合;综合(ⅰ)(ⅱ)(ⅲ)得a=4或-6. 简评:①作出f(x)“斜底桶形”图后,解集不空的充要条件是直线y=m在函数f(x)图象最低点的上方,图象简单明了,思维简洁;②分类作出f(x)“斜底桶形”图后,单调性尽收眼底,f(x)最小值均在x=a处取得. 例3 (2016年全国卷Ⅰ)已知函数f(x)=|x+1|-|2x-3|,①画出f(x)的图象;②求不等式|f(x)|>1的解集. 解:①零点分段得 图12 图13 ②由|f(x)|>1得f(x)>1或f(x)<-1,(ⅰ)当f(x)>1时,结合图13知,令-x+4=1,得x=3;令3x-2=1,得x=1,依图象高低得f(x)>1的解集是{x|1 简评:此高考题考查了画“开口向下小鸟形”图象的能力,解绝对值|f(x)|>1不等式要分两类处理,依据图形很快锁定直线y=±1与y=f(x)图象交点的大概位置,从而为下一步代数精确求解埋下伏笔. 图14 例4 设函数f(x)=|x+3|,g(x)=|2x-1|,①解不等式f(x) 解:①分别作出f(x)和g(x)图象,而g(x)= 图15 要使h(x)>r(x)恒成立,从图15审视,就是h(x)图象永远在r(x)直线上方.(ⅰ)当a≥0时,临界线是r(x)=ax+4与y=4x+5平行,此时满足0≤a≤4;(ⅱ)当a<0时,临界线是r(x)=ax+4过顶点A(-3,7),此时应满足h(-3)>r(-3),得7>-3a+4,即a>-1,又a<0,所以-1 简评:第①问可以借助两个∨形图,形象地求出交点横坐标,进一步利用图象高低关系确定解集范围;满足第②问条件的是直线系,关键是精准确定两边的临界线,再依直线系的旋转走向确定斜率a的取值范围. 图16 解:①分段得f(x)= ②零点分段得 图17 简评:此题考查了“开口向上小鸟形”图象,第②问作出f(x)图象后方能准确判断所围成的三角形,以及底和高等边长怎样求解.缺少图解,难找思维切入点. 例6 (2017年全国卷Ⅰ)已知函数f(x)= -x2+ax+4,g(x)=|x+1|+|x-1|,(1)当a=1时,求不等式f(x)≥g(x)的解集;(2)若不等式f(x)≥g(x)的解集包含区间[-1,1],求a的取值范围. 解:(1)依题知f(x)=-x2+x+4,即f(x)= 图18 图19 简评:此题考查了“平底桶形”与“上凸的抛物线”模型.在第(2)问中,不等式f(x)≥g(x)的解集包含区间[-1,1],在区间[-1,1]上截图,解析为在区间[-1,1]内,f(x)局部图象上的点不能低于g(x)局部图象(即桶底水平段)上点,又因为抛物线段是上凸的,所以只需满足f(1)≥2且f(-1)≥2就足够了. 例7 (2017年全国卷Ⅲ)已知函数f(x)=|x+1|-|x-2|,(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范围. 图20 解:(1)依题意两边构造函数y=1和f(x)= 图21 简评:此题考查了“右向游泳形”图象,处理第(2)问时,首先要弄清楚抛物线与线段EF刚接触时,是相切接触,还是非相切接触,因为它决定着求m临界值的方案. 感悟:解“与含两个绝对值之和(差)或一个绝对值”相关联的不等式问题,可以用直观图解法(是教材构造法的延展),整体挖掘两边不等关系的几何意义,以图导思、以图助思、以图促思,从而转化为代数的不等关系并求解.图解法的好处是显而易见的,就是缩短思维的长度和降低思维的难度,整体把握结果的可能性,使问题暴露在阳光之下,能居高临下地透过题目迷人的包装表象,窥探到问题的本质,直击目标,让人有一种拨云见日的快感. 上面节选的例题全面涵盖了含两绝对值之和(差)或一个绝对值的函数的十种函数图式,熟悉这十种函数的图式,能提高作图速度与准确性.图解法具有很浓的程序化解题步骤,操作性强,可概括为几步:整理后左右两边分别构造函数(具备了的函数可免这一步)→化为分段函数→正确作图→依两个图象间的高低信息解决相关问题.其中作图显得尤为重要,是最关键的一步,只有熟悉这十种图式才能达到有章可循的境界,提高算理能力.