不依赖GPS的磁信标导航定位系统

孙之光，刘剑威

(江苏自动化研究所，江苏连云港 222061)

随着科学技术的不断进步，国内外定位导航技术[1]快速发展，广泛应用于海、陆、空等多个领域[2]。现在有各种各样的导航技术，如天文导航系统[3]，惯性导航系统(INS)[4]，全球定位系统(GPS)[5]， ZigBee技术[6]等等。但是这些系统都有各自的优缺点。我们都知道，天文导航系统的特点是误差不会随时间累积，但它会受到大气环境的影响。INS是一种自主导航的方法。然而，它的位置误差随着时间的推移而累积。GPS可以实现全天候、全球和高精度的连续导航和定位，但GPS接收机在GPS信号弱的偏远地区无法定位。对于ZigBee而言，随着ieee802.15.4商业标准的逐步完善，低功耗、短延时、大网络容量等诸多优势已经显现[7]，但它只能专用于专用网络，不适用于应用场景的高传输速率。

除上述外，在许多情况下，传统的导航方法无法工作，如地球物理勘探、水下通信、隐藏式生物应用探测、救援应用导航定位、室内自助机器人导航等。因此，本文提出了一种不依赖GPS的磁信标导航定位技术。此外，EKF[8]数据融合的使用，使得方法具有独立性强、成本低、隐蔽性好等优点。

1 磁信标定位原理

所提出的磁信标导航方法依赖于水平方向上的磁矩，因为水平方向产生的磁场受导电性土壤影响较小。相反，垂直方向上的磁矩明显减弱是由于导电土壤的作用。

在磁性方面，19世纪早期提出的比奥-萨瓦特定律，可用来描述电流源和磁场之间的关系

(1)

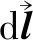
M=A·N·I

(2)

磁矩是由右手定则在电流绕组方向上确定的方向，与线圈轴方向一致，是线圈方向的大小矢量。线圈产生的磁场可以表示为偶极子场，其距离大于线圈的最大大小，但小于励磁电流的电磁波长。磁通密度可以表示为

(3)

因此，磁场强度H可由式(3)计算：

H=r-5[3(M·r)r-Mr2]

(4)

这里，根据磁感应强度和式(3)磁场强度的关系，可以简化和省略系数(μ0/4π)，从式(4)可以看出，磁场强度H的大小是磁矩M和r-3的线性函数。

我们已经知道，信标磁场可能受到土壤成分的影响，含水层具有较高的电导率，可以使磁场变形。磁标模型受水平磁矩的影响，而水平磁矩受垂直磁矩的影响。因此，对于磁标模型的应用，建议使用具有水平磁矩的信标，否则导电土将会增大磁场强度，从而导致更大的误差。

接下来，介绍了利用磁信标的两种不同的目标定位方法，这两种方法采用用于低频磁场的双轴传感器[9]。

1.1 方法1——使用几个集中的信标导航和定位

我们假设一个导航目标物体在二维平面内移动，所以我们可以用两个坐标来描述它在x-y平面上的位置，因此，可以通过(3)计算磁场强度

(5)

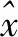
(6)

从式(4)和式(5)可以计算出磁场强度H1与磁矩M1之间的关系如

(7)

我们用a1来定义xy坐标轴两个分量的比例

(8)

化简式(8)，得到方程

2x2-3a1xy-y2=0

(9)

计算式(9)，求出方程的解

(10)

因此，我们/定义，以反映/、/坐标之间的比例因子

(11)

对于位于二维坐标下的磁传感器，从式(7)第一个信标测量磁场强度为H1，第二个信标的磁场H2(接收器的微小距离可忽略)，H2可以表示为

(12)

(13)

将x的表达式(10)代入式(13)，

(14)

上面的公式表示为y

(15)

图1 在笛卡尔坐标系中的磁信标

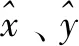
1.2 方法2——使用一对间隔的信标导航和定位

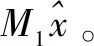
x=k1y

(16)

类似于式(16)我们可以为信标3编写相应的关系

x=k3(y+R)

(17)

类似于式(9)，我们可以写出

(18)

因此，因子k3可以表示为

(19)

从(16)和(17)，消除x得到y

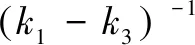
(20)

对于式(11)和式(19)，上面的上标对应于x和y有相同的符号的情况，而下标代表有x、y相反符号的情况。因此，在选择k1和k3值的时候，我们需要注意考虑具体的情况。k1、k3在这样的条件下，我们可以使用(17)和(20)来寻找特定的x和y值，从而达到使用磁信标定位的目的。

1.3 扩展卡尔曼滤波器在目标跟踪中的应用

上述两种导航算法针对某一特定位置，从而忽略了相应历史因素的位置。这远远不能用于磁信标导航。因此，对于这个非线性系统滤波问题，我们考虑扩展卡尔曼滤波(EKF)递归方程的应用来跟踪和定位：

(21)

P(k+1|k)=Φ(k+1|k)P(k|k)ΦT(k+1|k)+

Q(k+1)

(22)

K(k+1)=P(k+1|k)HT(k+1)

(23)

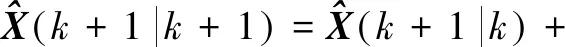
(24)

P(k+1|k)=[I-K(k+1)H(k+1)]P(k+1|k)

(25)

在上述方程中，滤波器初始值X(0)和滤波器误差方差矩阵的初始值P(0)分别为:

X(0)=Ε[X(0)]，P(0)=var [X(0)]

其中，状态转移矩阵Φ(k+1)和观测矩阵H(k+1)可以用雅可比矩阵f和h代替，

(26)

(27)

假设目标是以速度v匀速运动的，目标在时间k的位置是s(k)。然后，在采样时间T后，目标位置为

s(k)=s(k-1)+vT

(28)

(29)

然后系统的状态方程是

C=ΦX(k)+ΓU(k)

(30)

式中，

(31)

假设k时刻，观测目标与观测时间点之间的距离为Z(k)，观测方程为

(32)

V(k)为传感器自身的测量误差，其方差为R。

根据方程(27)，我们可以得到雅可比矩阵H，

(33)

将式(29)和式(32)代入式(33)，得到

(34)

2 磁信标导航系统

2.1 磁信标导航系统构建

磁信标定位系统包括激磁装置、功率放大器、磁信标线圈、信号接收器和定位计算机等。激磁装置产生指定频率的激磁信号，该信号经功率放大器放大后给磁信标，在磁信标周围的空间就产生了指定的磁场，多套磁信标组合同时工作就在空间中产生了叠加的磁场，在目标位置处的高精度磁信号采集处理单元的磁传感器可以测量该信号，该信号经过处理，可以计算出该位置与磁信标的空间方位关系，从而实现动态实时定位。

2.2 磁信标激磁装置设计

直接数字式频率合成器(Direct Digital Synthesis-DDS)，具有高精度、快速变换频率、输出波形失真小等特点，产生的数字波形(通常是正弦波形)，经过模拟滤波器后，得到最终的模拟信号波形。DDS基本结构框图如图2所示。

图2 DDS的基本结构框图

2.3 磁信标功率放大器设计

设计基于OPA541的功率放大器，具有40 V电源供给能力，以及持续5 A电流输出能力。内部集成电流限制电路可通过单一的外部电阻实现。通过将功率级驱动电流分流，使功率级器件不会因过载而损坏。

2.4 磁信标线圈的设计与实现

在本次设计中，我们用到的信标是100 cm×100 cm的正方形线圈，为了能够满足水下实验要求，使用的线是尼龙皮密封纯铜线，匝数是230匝，左右两个线圈的电阻分别为4.8 Ω和5 Ω。

2.5 磁通门传感器设计

磁通门电路由两部分组成，即激磁电路、信号处理电路。磁通门信号处理电路原理如图3所示，主要处理过程：选频放大、相敏检波、积分滤波和反馈环节。

图3 磁通门信号处理原理框图

通常情况下，由于受到加工及安装工艺的限制，磁强计会出现零偏误差、三轴灵敏度不一致、三轴很难完全正交等问题，引起磁强计的测量误差，因此在使用磁强计之前要对其进行标定。本文中利用labview设计程序对磁强计的磁强进行零偏标定。

2.6 软件设计

磁场测量的软件包括三个部分，分别为数据的读取、处理和显示。

数据的读取用到Socket协议，数据显示用到MFC，处理数据采用的是FFT(快速傅里叶变换)方法进行滤波选频。

将经过FFT处理的固定频率的幅值代入分离式双信标定位算法中，即可计算出测试点相对于信标的位置。整个程序的流程图以及显示界面如图4所示。

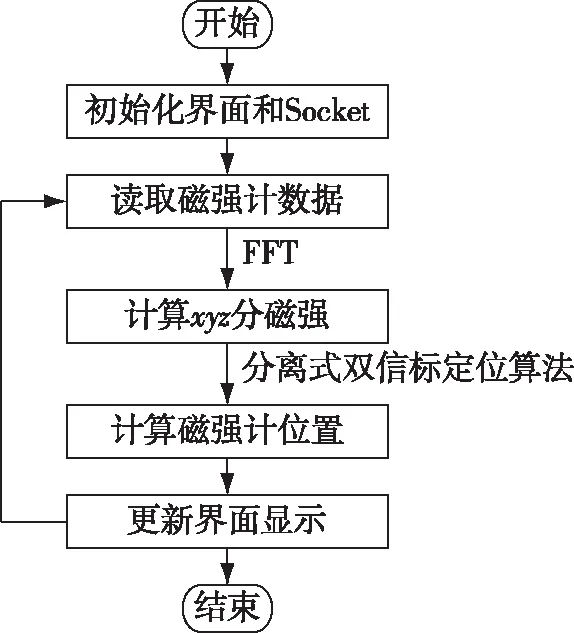
图4 数据读取、显示与处理程序

3 仿真与试验验证

3.1 仿真计算

在仿真过程中，为了证明跟踪的优点，我们选择了一个10 m×11 m的区域，分为大小1 m间隔的网格。采样周期是1 s 。目标的运行速度是恒定的7.2 m/s。接收轨迹包括24个连续步骤。每个站点都添加了0均值和1pT标准偏差(STD) 的高斯白噪声。另外，我们设置了τ为1000。

磁信标的具体设置如表1所示，

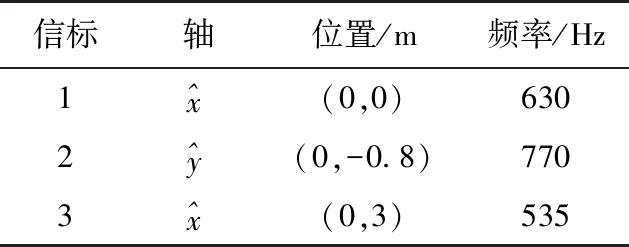
表1 模拟信标具体参数

接收器的位置通过24步改变，对应的实际轨迹和融合轨迹误差对比如图5所示。

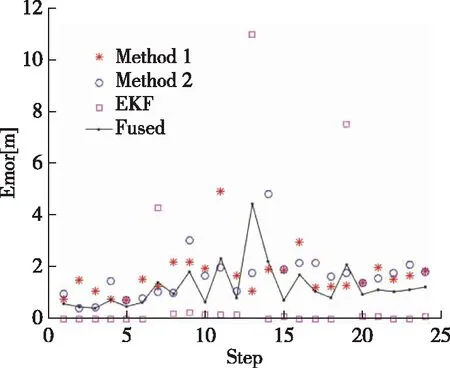
图5 仿真误差对比

利用上述仿真条件和参数设置进行仿真，融合方法所构建的连续位置的估计轨迹与实际轨迹非常接近。

3.2 实验验证

利用上文中的定位理论，设计的磁信标定位系统如图6所示。定位结果如表2所示。

从试验测量数据来看，x轴方向误差均值为-10 cm，均方差为118 cm，y轴方向误差均值为38 cm，均方差为29 cm。

图6 一对信标定位导航系统

序号实际位置/cm测量位置/cm误差/cm1(1100,-300)(995,-270)(-105,30)2(1100,-600)(1059,-526)(41,74)3(1100,-1300)(1275,-1291)(175,9)4(1500,-900)(1424,-837)(-76,63)5(1500,-1000)(1415,-986)(-85,14)

4 结束语

本文给出了一种不依赖于GPS的导航系统。介绍了两种简单实用的磁标定位方法。该方法使用磁场信标定位具有磁接收器的目标对象。通过扩展卡尔曼滤波和数据融合方法，提高了导航定位方法的精度。仿真结果表明，该方法对自主车辆导航、地下隧道映射、室内机器人定位等许多实际应用都是有效的。这使得磁标导航定位，无须依靠传统的定位条件，也能达到良好的定位效果。本文下一步需要针对钢铁等磁质被磁化而导致的测量误差进行深入的研究。