雷达/电子干扰攻防对抗信号级仿真中提高仿真速度的思考和实践

邱丽原,孙伟超

(海军航空大学,山东烟台 264001)

数字计算机仿真(以下简称为计算机仿真)以相似原理为基础,结合模型理论、系统技术、计算机技术、信息技术以及应用领域的相关专业技术[1],在现代武器装备的论证、设计、制造、试验、定型、训练,特别是对抗性验证、评估中得到广泛而深入的应用,取得了很好的军事效益和经济效益。

现代信息化战争的一个最显著的特点就是电子战的作用和地位日益突出,甚至可以说,电子战水平和应用能力的高低,在很大程度上决定了战斗和战役的胜负。雷达和针对雷达的电子对抗是电子战中最主要的内容和攻防矛盾之一,应用计算机仿真对雷达/电子干扰攻防对抗进行研究非常必要。

雷达/电子干扰攻防对抗计算机仿真可以粗略分为功能级仿真和信号级仿真两大类,在满足了真实性要求的前提下,信号级仿真最突出的问题就是仿真速度的问题。在本文中,我们结合多年从事雷达/电子干扰攻防对抗信号级仿真的体会,就提高雷达/电子干扰攻防对抗信号级仿真的仿真速度的问题进行一些讨论,主要包括以下内容:

1) 信号级仿真的必要性；

2) 信号级仿真的速度问题及其解决出路；

3) 从仿真软件本身找速度问题的解决出路。

1 信号级仿真的必要性

关于什么是信号级仿真,什么是功能级仿真的问题,在国内有不同的看法[1]。简而言之,我们认为,对于相参雷达,能够再现雷达内部的零中频及其以下的信号流动流程及其处理过程;对于非相参雷达,能够再现雷达内部的视频及其以下的信号流动流程及其处理过程,就是信号级仿真。而功能级仿真,通常仅涉及空间能量计算以及一些基于概率计算的随机变量门限检测,而不涉及雷达内部的信号流动流程及其处理过程。

从信号级仿真和功能级仿真的作用和实际效果看,在雷达/电子干扰攻防对抗仿真中,有以下区别。

1)客观还是主观的区别

信号级仿真要求把雷达本身真实地仿出来,把干扰机产生的干扰信号真实地仿出来,还要求把目标和环境也真实地仿出来。攻防对抗的结果,是通过运行仿真软件来产生的,是客观的。而功能级仿真在多个环节上都要有人的主观参与和决策,特别是一些关键的结论性数据,要由“专家”人为设定,因而有很强的主观性。

2)能不能实现的区别

由于在信号流动流程及其处理过程的层面对雷达、干扰信号、目标信号和环境信号进行真实的仿真,在信号级仿真中,所有的干扰都可以加入雷达中。而在功能级仿真中,一些干扰是加不到雷达中的。换句话说,一些干扰在功能级仿真中不能实现,因而是得不出结果的。特别是欺骗性干扰(一个典型的例子是距离波门拖引干扰),信噪比虽然是重要因素,但已经不是决定性因素,决定性因素是目标回波信号、干扰信号在雷达组件中的相互作用以及雷达组件对信号的处理。对欺骗性干扰进行功能级仿真既没有针对性,也没有实际意义。

另外,除个别情况外,对于雷达/电子干扰攻防对抗中至关重要的目标识别,无法进行有意义的功能级仿真。

3)误差与颠覆的区别

毋庸讳言,任何仿真都是有误差的,信号级仿真也不例外。但功能级仿真与实际情况的差别在一些场合下是颠覆性的。以反舰导弹末制导雷达为例。反舰导弹末制导雷达在受到舰载有源压制式干扰时,按照功能级仿真通常使用的信噪比准则,由于信噪比极低,在末制导雷达中已经看不到目标回波,干扰是成功的。但实际情况是,在这种情况下,末制导雷达会启动杂波源跟踪(HOJ)功能,继续在方位上跟踪水面舰艇目标,引导反舰导弹准确命中,从而使得干扰彻底失败。

综上所述,我们认为,对于雷达/电子干扰攻防对抗而言,要进行客观、全面、准确的研究,信号级仿真是非常必要的[2]。

2 信号级仿真的速度问题及其解决出路

相对于功能级仿真,信号级仿真有一些特别突出的问题,例如仿真速度问题,模型校核问题[3]等。在满足了真实性要求的前提下,信号级仿真的一个最引人关注的问题就是仿真速度的问题。信号级仿真速度慢,主要原因在两个方面：一是计算内容多而且细致导致的计算量大；二是计算频率高。以非相参雷达为例,系统采样频率需要达到20 MHz。这两个方面的因素是由于信号级仿真本身的性质决定的,是无法改变的。

信号级仿真的速度慢主要导致三个方面的问题：一是一次仿真要花费很长的时间,效率太低,同时也影响了仿真应用者对重点问题的关注;二是极大地限制了信号级仿真在系统层面、体系层面上的应用;三是不能用于任何有硬件参与的研究,包括模拟训练等。

虽然计算量大、计算频率高是信号级仿真的天然特性,但提高其仿真速度,使其达到实时或近实时(这里的近实时指的是：名义时间∶计算机时间<=1∶3)还是大有可为的。从通用的角度看问题,提高信号级仿真的速度有赖于在以下方面取得突破:

1)计算机硬件的整体速度有大幅度的提高;

2)计算机的多核并行处理能力有大幅度的提高;

3)通过辅助硬件加速使计算机系统的速度得到大幅度的提高;

4)使仿真软件本身的运行速度得到大幅度的提高。

第一个方面,计算机硬件的整体速度,至少涉及CPU、内存、主板等多个硬件(或硬件组件)的速度以及整合速度,这里主要拖后腿的是内存(也涉及主板和总线)的存取速度。除非出现系统性的技术变革,要计算机硬件的整体速度有大幅度的提高是不现实的。

第二个方面,计算机的多核并行处理能力的大幅度提高,在今天已经成为技术现实。多核并行处理能力的提高,通过多个实体仿真软件(多枚反舰导弹同时攻击水面舰艇目标情况下,每一枚反舰导弹的末制导雷达都是一个实体仿真软件)的并行运行,可以提高整个仿真系统的运行速度,但对于构成真正瓶颈的单个实体仿真软件的速度提高则没有意义。实际情况下,不大可能为了多核并行处理,把一个实体仿真软件拆分成为多个部分。这里有三个问题:

1)能不能并行的问题

并行计算是需要条件的。或者说,并不是任何实体仿真软件的任何部分都能够任意地拆分来进行并行计算的。一个实体软件的某些部分要能够并行,必须满足一定的时序、逻辑或计算关系。事实上,对于一个雷达的仿真软件实体而言,能够进行拆分进而进行并行计算的部分是非常有限的。

2)并行化改造的代价

无论是对一个已经完成的实体仿真软件进行拆分并行化改造,还是在设计、编制一个新的实体仿真软件过程中贯彻并行化,都需要在较深的技术层次上付出较大的人力和时间代价。

3)并行化执行的代价

在并行化执行一个实体仿真软件时,相应的通信/控制、数据分配、数据合并和数据(包括程序)存取/传输等,都是要付出时间代价的。特别是最后一个环节,由于涉及的是不同核之间的数据/程序的传输和存取,会付出相当大的时间代价。

当并行化执行的代价接近甚至高于并行化带来的收益的时候,并行化就失去意义了。

由于上述三个问题的存在,要利用计算机的多核并行处理能力的大幅度的提高来提高单个实体仿真软件的运行速度是没有普遍意义的。

第三个方面,通过辅助硬件加速使计算机系统的速度得到大幅度的提高。通行做法有两条途径：一条途径是采用FPGA或FPGA+DSP构建专用的辅助硬件;一条途径是采用GPU等通用辅助硬件。

采用FPGA或FPGA+DSP构建的专用辅助硬件,的确能够大幅度提高单个实体仿真软件的运行速度,除了构建专用辅助硬件需要付出的成本和人力/时间代价外,其最大缺点是灵活性差。

GPU从本质上看是一种并行多核,而且其处理单元数比CPU中的核数高好几个量级。除了上述的多核并行处理的三个问题外,GPU并行处理还有一个特殊的问题,就是其处理深度很浅,因而需要频繁地交换数据,在这个方面会付出更大的时间代价。有GPU方面的资深专家给出了一个例子[4],对于同一个问题(该问题比较复杂,具体内容在此不拟赘述),采用程序优化和GPU加速两种方法,GPU加速方法的速度仅比程序优化方法快一倍。我们认为,GPU加速的适用面受到很大的限制。

第四个方面,使仿真软件本身的运行速度得到大幅度的提高,在下面作为一个专题,进行一定程度上的展开讨论。

3 从仿真软件本身找速度问题的解决出路

从理论和实践两个方面看,从仿真软件本身找速度问题的解决出路,使仿真软件本身的运行速度得到大幅度的提高,是大有可为的。基于我们的具体实践,以下列出四条基本思路或者说是基本技术方法:

1)提高模型抽象和实现的层次和水平;

2)提高算法优化的层次和水平;

3)提高以空间换时间的水平;

4)提高数据存取的速度水平。

3.1 提高模型抽象和实现的层次和水平

提高模型抽象和实现的层次和水平,在一定意义上,对于提高仿真软件的运行速度具有根本的、普遍的意义和作用。

系统仿真以模型为基础,在本质上是模型试验,仿真运行主要就是模型的运行。模型的有效性和精度决定了仿真的有效性和精度,模型也决定了仿真软件运行的计算量。这里所说的通过提高模型抽象和实现的层次和水平来提高仿真软件的运行速度,以保证模型的有效性和精度不下降为基本前提。

本文以目标回波的仿真为例阐述模型抽象的问题。这里仅考虑回波的时间位置和标准波形(与发射基带波形相同的单位幅度的波形,这里采用简单矩形脉冲)。

很多使用Matlab/Simulink进行仿真的人,在一开始的时候会用如图1所示的模型一来实现目标回波的仿真。

图1 回波仿真的模型一

图1中的目标回波延迟时间根据目标与雷达之间的距离计算而得。

在图1的模型中,目标回波由发射脉冲经目标回波延迟时间的延迟得到,在物理概念上是完全正确和精确的。但图1的模型的实现效率是非常低的:其中的可变时间延迟器(Variable Time Delay)模块在内部通过存储器来存储一个指定时间范围内的最新输入数据。在每一个系统仿真步长(0.1 us量级)中,除了新数据输入外,存储器中的所有已有数据(数量在10 000量级,具体值与系统仿真步长和雷达的脉冲重复周期有关)都要依次向后挪移一个存储单元。由此使得仅仅是单个目标的回波的仿真就会消耗计算机的很多时间资源。

模型一效率低的主要原因是大量存储器数据的高频率的位移。分析后发现,这种导致低效率的位移实际上是不必要的。对目标回波的生成过程进一步抽象后可知,发射脉冲的波形延迟可以用其发射后时间的延迟来替代,因而可以得到实现目标回波仿真的模型二,如图2所示。

图2 回波仿真的模型二

比较图1和图2可以看到,图2中用重复序列产生器(Repeating Sequence)取代了图1中的脉冲产生器Pulse Generator,而且没有了可变时间延迟器。在图2中,不再直接产生发射脉冲(概念上,发射脉冲还是要产生的),而是代之以产生以发射脉冲为起点的时间;再没有通过发射脉冲的延迟来产生目标回波,而是直接用以发射脉冲为起点的时间与目标回波延迟时间进行比较,一旦达到目标回波延迟时间即产生目标回波。

理论分析和实际的仿真运行测试都表明,在相同输入的条件下,上述的模型一、模型二的输出完全相同。明显不同的是,模型二的仿真速度几乎是模型一的10倍。这还只是针对单目标的情况。在多目标的情况下,仿真运行测试表明,模型二的仿真速度优势更加突出:如果目标数为N,则模型二的仿真速度几乎是模型一的10×N倍。

这个例子说明,提高模型抽象和实现的层次和水平对于提高仿真软件的运行速度可以具有非常显著的作用。

3.2 提高算法优化的层次和水平

在科学技术的发展历史上,通过算法优化提高运行和处理速度的事例不胜枚举。针对离散傅里叶变换DFT进行快速计算的快速傅里叶变换FFT是最著名的一个例子。FFT的发明为DFT的广泛应用创造了良好的条件。

针对不同的具体问题,算法优化的具体方法可能千差万别,但还是有一些共同的规律可以摸索和遵循。例如,已有计算结果的重用(重复使用)、避免数据的不必要的移动等。本文以在雷达信号级仿真中经常会遇到的非相参脉冲滑窗积累(滑窗宽度设为M)的算法优化为例来进行说明。

简而言之,非相参脉冲滑窗积累就是对于雷达接收机在连续M个脉冲重复周期中的视频输出数据按距离单元相加,其基本原理如表1所示。

表1中,L表示一个脉冲重复周期中的距离单元数,当前的脉冲重复周期编号为N+M-1,要与前面的编号直到N的各个脉冲重复周期(一共是M个脉冲重复周期)中的数据按距离单元相加。

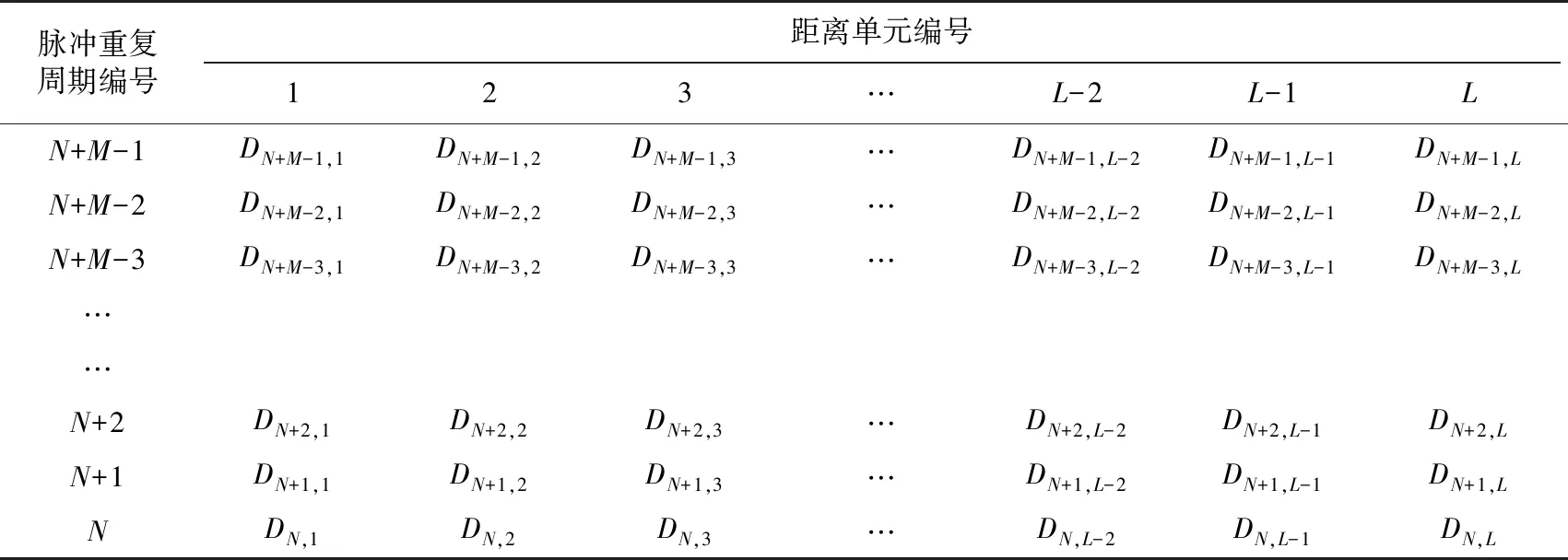
表1 非相参脉冲滑窗积累原理示意表(按距离单元进行M个脉冲重复周期的数据相加)

由表1所示的非相参脉冲滑窗积累原理可知,如果直接实施非相参脉冲滑窗积累,在每一个脉冲重复周期,对于每一个距离单元,M个数据相加,需要进行M-1次加法。

进一步分析可知,以距离单元K为例,在一个脉冲重复周期进行相加的M个数据(相加结果记做SN+M-1,K)中,前M-1个数据的相加在上一个脉冲重复周期中已经完成,仅需从上一个脉冲重复周期的积累数据(SN+M-2,K)中剔除(减去)最早的脉冲重复周期的数据DN-1,K即可得到;再加上本脉冲重复周期中的新数据DN+M-1,K即得到完整的SN+M-1,K。换句话说,对于滑窗宽度为M的非相参脉冲滑窗积累,在每一个脉冲重复周期,对于每一个距离单元,仅需进行1次加法和1次减法(以下简称为1+1算法),而无须进行M-1次加法。显然,这种1+1算法的效率明显高于要进行M-1次加法的直接算法。滑窗宽度越宽,1+1算法的效率提高越显著。

以下给出一次完成一个脉冲重复周期中所有距离单元的非相参脉冲滑窗积累的1+1算法的Matlab程序。

程序中用到以下变量:

aIQinput:存储当前PRI(PRI为脉冲重复周期)输入的正交双通道复数数据的数组(行数组,数组元素对应于距离单元,以下除I-Row外类似);

aTempAbs:存储当前PRI的要进行非相参积累的视频数据的数组;

aIntegrationData:存储当前PRI的非相参积累结果数据的数组；

aStoreCD:存储当前滑窗中输入视频数据的数组;

I-Row:aStoreCD的行指针;

Width-SW:滑窗宽度M。

除初始化部分外,1+1算法的Matlab程序中仅需要以下四条中的后三条语句:

1)aTempAbs=abs(aIQinput);

2)I-Row=mod(I-Row,Width-SW)+1;

3)aIntegrationData=aIntegrationData+aTempAbs-aStoreCD(I-Row,:);

4)aStoreCD(I-Row,:)=aTempAbs;

第1)条语句的作用是由当前PRI的正交双通道复数数据aIQinput得到要进行非相参积累的当前PRI的视频数据aTempAbs。显然,该语句不属于1+1算法。

第2)条语句的作用是行指针I-Row以滑窗宽度Width-SW取模后加1,以循环指向aStoreCD中最早的脉冲重复周期的输入视频数据,该数据在本次积累中应该剔除。

第3)条语句的作用是具体实施1+1算法,得到当前PRI的非相参积累结果数据。

第4)条语句的作用是以当前PRI的新数据更新(替换)存储aStoreCD中当前被剔除的旧数据。

在上述程序中,通过1+1算法,在最大的程度上做到了已有计算结果的重用;通过aStoreCD数组和I-Row指针的应用,避免了数据的移动。通过这样的算法优化,有效地提高了仿真软件运行的速度。

3.3 提高以空间换时间的水平

狭义地讲,以空间换时间就是以计算机的存储空间资源换取计算机的时间资源,提高计算机的运行速度。以空间换时间的最简单也是非常有效的例子之一就是通过查表法来避免复杂计算,直接得到相关数据结果。下面以FFT为例进行说明和讨论。

对于sin()等连续函数的数值计算[5],最容易想到的是采用泰勒级数。对于sin(x),有

取上式的前三项(5次多项式)来近似计算sin(x),得到

在|x|≤1的范围内,P5(x)的误差小于1/7!≈2×10-4。按照高效的多项式计算的秦九韶算法,计算一次P5(x),需要进行5次加法和5次乘法。

除了泰勒级数外,对于sin()等连续函数的数值计算,用得更多的是精度更好、计算效率更高的切比雪夫插值法。对于sin(x),其切比雪夫插值法近似为

sin(x)≈-1.2 850 635×10-3x6+0.0 121 117x5-6.0 244 134×10-3x4-0.16 137 988x3-2.357 414×10-3x2+1.0 004 218x-1.32 648×10-5

在0≤x≤π的范围内,上式的误差小于1.5×10-5。

用秦九韶算法,按上式计算一次sin(x),需要6次加法和6次乘法。以下关于计算量的计算以采用切比雪夫插值法的秦九韶算法为准。

一个复指数幂数据的计算包括二个sin()的计算(一个sin()和一个cos()),每个sin()的计算需要6次加法和6次乘法,粗略认为两次实数乘法和加法分别与一次复数乘法和加法相当,则一个复指数幂数据的计算需要6次复数乘法和6次复数加法。

众所周知,对于N点(N为2的整数次幂)FFT,其复数乘法和加法的次数都是Nlog2N。关于复指数幂数据的计算量可以有两种不同的衡量方法。

第一种方法:FFT中的复数乘法实际就是输入信号数据等与复指数幂数据的相乘。N点FFT中,Nlog2N次复数乘法要计算Nlog2N次复指数幂数据,而计算Nlog2N次复指数幂数据的计算量为6Nlog2N次复数乘法和加法,是FFT算法本身计算量的6倍。

第二种方法:N点FFT中需要用到的复指数幂数据仅为N个。这N个数据中,有的会多次用到。如果一个复指数幂数据计算后即存储保留,在需要的时候再重用,则N点FFT中,复指数幂数据的计算量为N×6次复数乘法和N×6次复数加法。换句话说,对于64点(log264=6)以下的FFT计算,复指数幂数据的计算量超过了FFT算法本身的计算量。FFT的点数越少,复指数幂数据的计算量的比重越大。

当FFT的点数N给定后,其所需要的N个复指数幂数据就是固定的了,可以在仿真程序外进行计算(线下计算),然后存入一个小数据表中。仿真软件运行过程中,在需要的时候通过查表读入复指数幂数据,相应的时间消耗可以忽略不计。上面的讨论表明,相对于线上计算,采用查表的方法获取复指数幂数据,对第一种方法,无论FFT的点数多少,计算速度可以提高6倍;对第二种方法,对于64点的FFT,计算速度可以提高1倍;对于32点的FFT,计算速度可以提高1.2倍;对于16点的FFT,计算速度可以提高1.5倍。

3.4 提高数据存取的速度水平

信号级的雷达/电子干扰攻防对抗仿真软件在目前的计算机(指PC机,以下同)上要提高运行速度,一条大有潜力的技术途径是提高数据存取的速度。

信号级的雷达/电子干扰攻防对抗仿真软件在目前的计算机上运行时,人们感觉运行缓慢,这是一种整体感觉。事实上,真正缓慢的、或者说成为仿真软件整体速度瓶颈的是计算机中的存储器(指内存,以下同)及其相关部件。因为很久以来,CPU的运行速度已经达到了存储器存取速度的100倍以上[6]。容易想到,如果能够提高存储器存取速度使其达到CPU的运行速度,仅此一条就可以大幅度提高仿真软件的运行速度,使信号级的雷达/电子干扰攻防对抗仿真软件的运行速度达到实时。但令人遗憾的是,全面、大幅度提高存储器的速度在目前以及可以预见到的将来都是做不到的,只能采取Cache等折中的办法。

Cache被称作缓冲存储器,其特点是速度快(比内存快10倍以上)但容量小。因其容量小,产生了命中率的概念。Cache的命中率定义为CPU需要的信息已经存在于Cache中的比率。显然,只有当CPU需要的信息已经存在于Cache中时,才能发挥Cache速度快的优势,真正提高仿真软件的运行速度。因此,提高Cache的命中率对于提高仿真软件的运行速度可以起到直接的、显著的作用。

Cache命中率的提高涉及多方面的因素,但数据/程序是否存入Cache在根本上遵循所谓的局部性原理[6]:在访问完一个内存区域后,程序会在不久的将来(时间局部性)访问邻近的区域(空间局部性)。

Cache的局部性原理可以在不同的层次、从不同的角度加以利用,以提高Cache的命中率。这里以Matlab中矩阵数据的存储和应用为例,来阐述和讨论一些典型问题。

众所周知,在Matlab的m语言中,矩阵数据是按列存储的。这就意味着,如果在组织矩阵数据的时候,把相关的数据组织到相同的列中去,在处理的时候也按列进行处理,将获得(相对于按行组织数据和按行处理)更快的处理速度。以下举例说明[7]。

问题:对于512×512的矩阵A,生成一个矩阵B,其元素按下式取值

对于本问题,可以用多种方法来求解。这里采用两种方法,分别对应于函数ForLoopCompare1(x)和ForLoopCompare2(x)。

方法一:

functiony=ForLoopCompare1(x)

y(512,512)=0;

tic;

fori=2∶511

forj=2∶511

fork1=-1∶1

fork2=-1∶1

y(i,j)=y(i,j)+x(i+k1,j+k2)/9;

end

end

end

end

toc

方法二:

functiony=ForLoopCompare2(x)

y(512,512)=0;

tic;

fork2=-1∶1

fork1=-1∶1

forj=2∶511

fori=2∶511

y(i,j)=y(i,j)+x(i+k1,j+k2)/9;

end

end

end

end

toc

下面,在相同的环境和相同的输入条件下比较两种方法的运行效率。

X=rand(512);

Y1=ForLoopCompare1(x);Elapsed time is 0.330648 seconds.

Y2=ForLoopCompare2(x);Elapsed time is 0.057423 seconds.

上述例子表明,对于同一个问题,Cache利用的差异可以导致接近6倍的速度差异。

在方法一的函数ForLoopCompare1(x)中,次数多的循环i、j放在外层,而且是按行的顺序从矩阵A(即x)中读取数据。按这样的方法,Cache基本不能发挥作用:对于每一个i、j和k1,k2=-1时取出的数据为x(i+k1,j-1),下一个要取出的数据为x(i+k1,j),再下一个要取出的数据是x(i+k1,j+1),各个数据在内存中的存储地址相差512×8字节(数据按double类型存储),第一个数据与第三个数据在内存中的存储地址相差8k字节,考虑到L1Cache和L2Cache的容量非常有限,这些要相继取出的数据是不可能同时被放入Cache中的。也就是说,这些数据只能从内存中读取,从而导致程序的运行速度低下。

在方法二的函数ForLoopCompare2(x)中,次数多的循环i、j放在内层,而且是按列的顺序从矩阵A(即x)中读取数据。按这样的方法,Cache的作用可以得到很好的发挥:对于每一个k2、k1和j,在i从2循环到511的过程中需要相继取出的509个数据在内存中是连续存放的;不仅如此,在k2、k1或j变化前后需要相继取出的数据在内存中也基本上是连续存放的,这就保证了Cache的极高的命中率,从而使得程序的运行速度得到很大的提高。

4 结束语

对于雷达/电子干扰攻防对抗信号级仿真,提高仿真软件的运行速度具有非常重要的意义。基于技术分析和多年的实践经验,我们认为,在当今的技术条件下,针对仿真软件本身挖掘潜力,对于提高速度仍然是大有可为的。以我们的亲身经历为例,我们研制了一个信号级的舰载多功能相控阵雷达仿真软件,最初的运行速度为1∶80,采取多种方法改进后,在原有功能不变,技术性能还有所提高的情况下,在相同的硬件环境中,使该仿真软件的运行速度提高近20倍,达到1∶4左右。所采取的方法就是上述的模型抽象、算法优化、以数据表格替换复杂计算、提高Cache命中率等。我们希望并相信,经过更加深入的艰苦努力,在国内同行的支持和共同参与下,雷达/电子干扰攻防对抗信号级仿真以及其他领域中具有计算量大和计算频率高特点的信号级仿真,在运行速度方面,能够有进一步的显著提高,从而使得信号级仿真在应用广度上得到大幅度的扩展,包括应用于系统层面、体系层面上的仿真,应用于有硬件参与的研究,如模拟训练等。