基于隐马尔可夫模型的舰船水下噪声评估方法
2019-10-12吴毅斌翟春平田作喜
吴毅斌,翟春平,张 宇,田作喜
(大连测控技术研究所,辽宁 大连 116013)
0 引 言
对舰船的水下噪声进行监测和评估,可及时发现异常状况,有针对性地指导舰船进行必要的检修和维护[1]。为方便对舰船的水下噪声进行监测和评估,通常在舰船进出港的航道上沉底布放测量传感器(水听器),将测量数据传输给岸上设备,对是否存在异常进行评估。关于异常,Hawkins 给出了本质性定义[2]:异常是在数据集中与众不同的数据,使人怀疑这些数据并非随机偏差,而是产生于完全不同的机制。判断数据是正常还是异常,属于数据分类问题。本文采用基于隐马尔可夫模型的模式识别方法,对舰船水下噪声进行评估判断。
1 隐马尔可夫模型
隐马尔可夫模型在语音识别领域有着广泛的应用,在水声领域也有相应的应用,如管景崇等在文章中验证了隐马尔可夫模型在线谱跟踪技术中的有效性和稳定性[3]。
1.1 基本特性
隐马尔可夫模型(HMM)是一种描述随机过程统计特性的概率模型,是由马尔可夫(Markov)链演变发展而来。与Markov 链不同的是,HMM 是一个双重随机过程,其中一个随机过程是具有有限状态的Markov 链,描述状态的转移;另一个随机过程描述每个状态和观察值之间的统计对应关系(隐含参数)。观察者只能看到观察值,不能直接看到状态,而是通过一个随机过程去感知状态的存在及其特性。HMM 根据观测信号的性质分为两类:连续隐马尔可夫模型和离散隐马尔可夫模型[4]。
1.2 模型描述
HMM 描述如下:
1)状态变量{q1,q2,…,qn},其中qi表示第i 个时刻的系统变量。状态变量通常是隐藏的,不可被观测的,也称为隐变量。设每个时刻有N 种状态,则取值范围为{S1,S2,…,SN};
2)观测变量{x1,x2,…,xn},其中xi表示第i 个时刻的观测值。观测值可以取连续值,也可以取离散值。每个时刻的观测值可能有M 种情况,取值范围为{O1,O2,…,OM};
3)HMM 的结构,在任意t 时刻,观测变量xt的取值仅依赖于状态变量qt,而qt仅依赖于t-1 时刻的状态qt-1(马尔可夫性),基于这种依赖关系,所有变量的联合概率如下式:
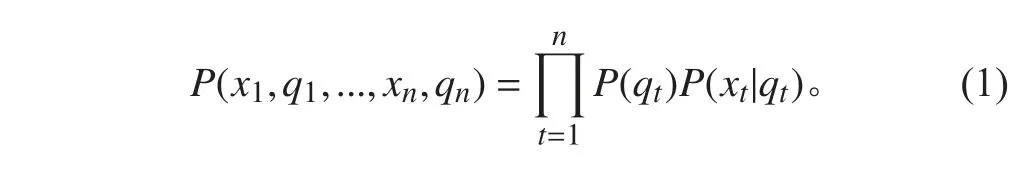
4)描述HMM 的3 组参数:
① 状态转移概率A:A={aij}N×N,其中aij=P(qi+1=Sj|qi=Si),1≤i,j≤N,即任意时刻t,若状态为Si,则下一状态为Sj的概率;
② 输出观测值概率B:B={bjk}N×M,其中bjk=P(xi=Ok|qi=Sj),1≤i≤N,1≤k≤M,即任意时刻t,若状态为Sj,则观测值为Ok的概率;
③ 初始状态概率π:π=(π1,π2,…,πi,…,πN),其中πi=P(q1=Si),1≤i≤N,即t=1 时刻,状态取值的概率分布。
因此,一个HMM 可简记为:λ=(π,A,B)。
1.3 主要应用
HMM 主要解决三类基本问题:
1)评估问题:计算给定模型λ 产生观测序列O 的概率p{O|λ};
2)解码问题:对给定模型λ 和观测序列O,求可能性最大的状态序列S;
3)学习问题:对给定观测序列O,在最大似然度下学习得到模型λ=(π,A,B):max p{O|λ}。
一般实际应用问题可以归纳为以上三类基本问题之一或者问题的组合。HMM 可实现对舰船的运行趋势进行预测,并且可以通过反映当前舰船状态信息的特征矢量代入训练好的HMM,经过模式匹配识别出舰船当前健康状态或者故障模式。
HMM 作为一种信号动态时间序列统计模型,非常适合处理连续动态信号,具有坚实的理论基础,还具有学习功能和自适应能力,能够通过训练获取知识来监测系统的状态。但是HMM 也有不足的地方:一是,HMM 为一种模式识别方法,强调的是其分类能力,但缺乏对故障本身的描述信息,对模型的学习参数不能够完全恰当的解释;二是,HMM 初始模型的选取仍是一个悬而未决的问题,仅是凭经验选取;三是,HMM 对于隐藏状态的物理意义不能给出恰如其分的解释。
2 信号特征参数提取
舰船水下噪声信号是时域信号,其数据不能直接送进HMM 进行处理,需要先对噪声数据进行分帧并提取特征参数,再进行VQ 矢量量化,得到一串观察序列后再送进HMM 进行处理。本文选取梅尔倒谱系数(Mel Frequency Cepstrum Coefficients,MFCC)作为特征参数,MFCC 是受人的听觉系统研究成果推动而导出的声学特征,在一定程度上模拟了人耳对语音的处理特点,因此表现相对比较稳健,是语音识别中常用的特征参数[5],陆振波也证明了MFCC 特征参数对于目标识别性能要好于AR 特征参数[6]。
MFCC 本质是提取功率谱中低频部分的包络特征,其提取流程如图1 所示[7]。

图1 MFCC 特征参数提取Fig. 1 MFCC feature parameter extraction
3 训练和评估
利用HMM 进行训练和评估时,必须输入一串可观测序列,以下称特征序列。需要先对舰船水下噪声信号数据进行一系列的变换,其步骤如下:
分帧:将一段时长的舰船水下噪声信号数据分成若干帧,分帧主要是为了后面构造一串特征序列,所分的帧数越多,对应的特征序列越长,原始信号如图2 所示。
提取MFCC:对每帧信号数据提取一个24 维的MFCC 特征向量,其中某一帧的MFCC 如图3 所示。
VQ 矢量量化:把一个多维特征向量看成是多维特征空间里的一个点,将特征空间分成若干块相互独立的子空间,给每块子空间定义一个字符,用这个字符来代表这个特征向量,所有帧的字符构成了一串特征序列,如下式:
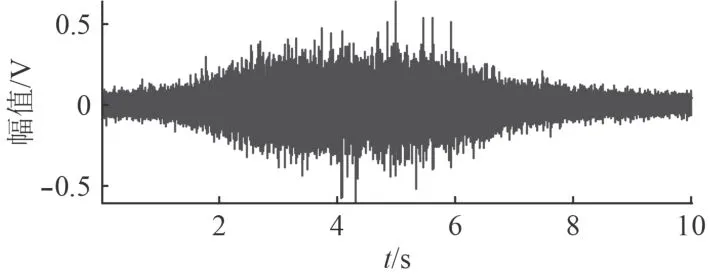
图2 原始信号Fig. 2 Original signal
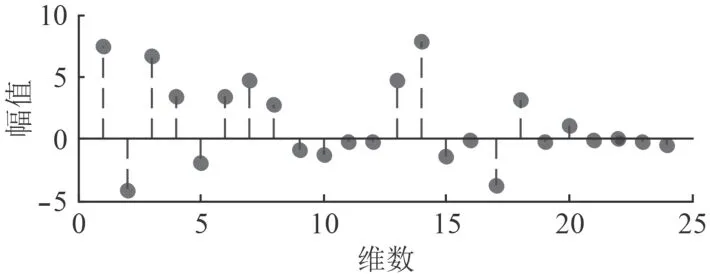
图3 某一帧的MFCCFig. 3 MFCC of a frame

训练时,将舰船正常状态数据样本对应的特征序列送进HMM 进行学习,得到正常状态对应的模型参数(A1,B1);将舰船异常状态数据样本对应的特征序列送进HMM 进行学习,得到异常状态对应的模型参数(A2,B2)。训练完毕后,将得到的正常状态和异常状态对应的模型作为评估模型,对待评估的舰船水下噪声信号数据进行评估,训练流程如图4 所示。
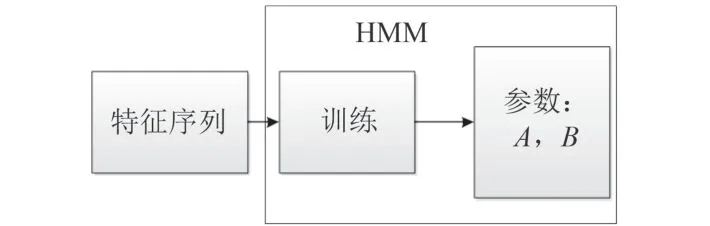
图4 HMM 训练Fig. 4 HMM training
评估时,先将待评估的数据样本变换成一串特征序列,再分别用正常状态和异常状态对应的模型来评估2 种状态发生的概率,概率明显大的,说明数据样本更符合这个模型对应的状态,该状态即为评估判断结果,评估流程如图5 所示。
4 算法实现中遇到的问题及解决方法
4.1 参数模型的初始化问题

图5 HMM 估计Fig. 5 HMM estimation
训练模型λ=(π,A,B)时,需要初始条件,包括初始隐含状态的概率矩阵π、初始隐含状态的转移概率矩阵A、输出概率矩阵B。一般取6 个隐含状态就满足分类识别需求,研究表明HMM 状态数并非越多越好,随着状态数的增加,附加熵逐渐趋于零,从而导致HMM 的信息熵逐渐趋于固有值[8]。由于训练需要多次迭代,A 和B 每次都会更新,故而A 和B 的初始条件对结果影响不太大,但合适的初始条件有利于在训练A 和B 时更快地收敛,另外A 和B 的初始条件要符合概率性质,即是概率矩阵每行元素的概率之和必须为1。
4.2 样本数量偏少问题
HMM 参数的训练取决于样本数量,样本数量越多,训练得到的结果越准确,但计算量也随之增加。由于实际应用时,有时样本获取存在困难,故而当样本数量过少时,会出现训练得出的输出概率矩阵B 的某个元素为0,这非常不利于机器运算,因为算法中会出现“0×lg(0)”的情况,由于这个值不收敛,所以机器计算某序列的概率时会返回“NaN”的结果,这不利于概率比较并输出识别判断结果。为了解决这个问题,在符合概率性质的前提下,可以赋予B 中那些为0 的元素一个极小值,例如0.000 1,这样可以避免结果出现“NaN”的情况,从而避免识别判断失败。
5 试验结果
5.1 试验方案
试验需要舰船水下噪声正常状态数据样本和异常状态数据样本,正常状态数据样本比较容易获取,而异常状态数据样本则极难获取。本试验选择舰船2 种不同工况下获取的水下噪声数据样本分别代表正常状态数据样本和异常状态数据样本,先从中选取训练样本对HMM 参数进行训练,然后再从中选取测试样本进行分类测试,以验证该算法是否适用于舰船水下噪声状况评估(分类)。针对2 种工况中的每种工况,选取101 个数据样本,其中1 个样本作为训练样本(时长10 s),另外100 个样本作为测试样本(时长2 s)。
5.2 训练
首先对训练数据样本进行预处理,包括端点自动识别、归一化和滤波等,处理后得到的仍然是10 s 的时域噪声数据。然后对数据样本进行分帧,每帧长为60 ms,帧间重叠30 ms,则10 s 的数据可拆分为332 帧数据。对每一帧数据提取MFCC 特征,得到一个24 维的特征向量,总共得到332 个24 维的特征向量。对这332 个特征向量进行矢量量化,把其看成是24 维特征空间里的332 个点,按照最邻近法对特征空间进行子空间划分,每个子空间用一个字符来表示,这样每个特征向量就用对应的字符来表示,得到332 个字符的特征序列。该序列送入HMM 进行训练,得到对应的模型参数。利用2 种工况的训练数据样本分别对HMM 进行训练,得到2 种工况对应的模型参数。
5.3 评估及结果
将测试数据样本按照与训练数据样本相同的方法进行预处理、分帧、MFCC 特征提取和矢量量化,得到一串特征序列,利用已训练好的2 种工况对应的HMM 参数来对待测试的特征序列进行最大似然评估,得到概率值,大概率对应的HMM 为最佳匹配模型,其对应的工况即为评估判断结果。利用2 种工况的测试数据样本各100 个,分别送进2 种工况对应的HMM 进行评估判断,每种工况对100 个测试样本的判断正确率均超过95%,结果如表1 和图6 所示。

表1 两种工况的识别结果Tab. 1 The recognition results under two conditions

图6 两种工况的识别结果Fig. 6 The recognition results under two conditions
6 结 语
本文将基于隐马尔可夫模型的模式识别方法应用于对舰船水下噪声进行评估判断。利用舰船在2 种不同工况下获取的水下噪声数据样本进行试验,结果表明,舰船水下噪声提取MFCC 特征后对HMM 进行训练,再利用HMM 进行评估判断效果很好。进一步增加训练样本的数量和测试样本的时间长度,可以在一定程度上提高判断的正确率,但对应的计算量也随之加大。MFCC 和HMM 相结合的分类方法,在语音识别领域有着非常广泛的应用,本文研究结果表明该方法也可以应用于舰船水下噪声状况评估。近年来发展起来的深度学习算法,在噪声处理和特征提取方面有着更优越的性能,已应用于水中目标识别、去噪和去混响等[9-11],该算法也适用于舰船水下噪声状况评估,正在进行相关研究。
