基于NSGAⅡ的交直流系统无功优化

武晓朦，王 欢

(西安石油大学电子工程学院 陕西省油气井测控技术重点实验室，陕西 西安 710065)

引 言

高压直流输电(high voltage direct current,HVDC)由于线路造价低、可快速调节电流和功率及远距离大容量输电的优势，近年来发展迅速。随着我国高压直流输电工程的不断投运，交流输电与直流输电的电网互联逐渐成为我国区域电网的主要方式。在直流输送大量电能的前提下，优化电网每个环节都能创造巨大的经济和社会效益，所以对于交直流系统无功优化的研究非常重要，交直流系统的无功优化也受到越来越广泛的关注[1]。

目前，国内外对于无功优化的研究主要是针对于交流系统单目标或多目标无功优化研究，而对于交直流系统的无功优化研究较少。现有基于交直流系统的无功优化算法大多以综合算法居多，大概分为传统算法与智能算法结合或者将两种智能算法结合的方式。文献[2]将遗传算法与内点法结合，遗传算法求解交流系统中少量的离散控制变量及直流系统控制变量，而采用内点法求解交流系统中大量的连续控制变量；文献[3]将对偶内点法和粒子群算法结合，考虑到交直流系统的变量有离散变量和连续变量共存，因此将无功优化分解为连续优化和离散优化两个部分，用内点法优化连续变量，粒子群算法优化离散变量，两种算法交替求解交直流系统无功优化问题；文献[4]结合了遗传算法与模拟退火法两种智能优化算法，在交直流系统无功优化过程中包含了遗传算法的复制、交叉、变异以及模拟退火法的状态产生函数等不同的邻域搜索结构。

随着对电力系统运行要求的提高，单目标无功优化已经不能满足电力系统的需求，以单一目标函数得出的最优解会使其他目标不能满足要求。因此综合考虑包括经济性、安全性等各类运行指标的多目标无功优化问题得到了广泛应用[5-6]。针对上述问题，本文将交直流系统总网损和节点电压偏移量作为双目标函数，求解交直流系统无功优化问题。

1 交直流系统模型

高压直流输电系统通常与交流系统互联，一起构成交直流输电系统，如图1所示。交直流输电系统以换流站相连，包含直流部分的换流变压器、整流器、逆变器和直流网络，以及交流部分的发电机、输电线路和变压器等[7]。

图1 交直流系统示意图Fig.1 Schematic diagram of AC/DC system

交直流系统的电压、电流、功率分别满足下列方程：

(1)

(2)

Ip=KαIs；

(3)

NUacIpcosφ=UdcIdc；

(4)

Pdc=NUacIpcosφ=UdcIdc；

(5)

Qdc=Pdctanφ。

(6)

式中：Udc、Idc分别为直流系统电压、电流，当为逆变器时Udc取-1；Uac为换流站连接交流母线电压；Nb为换流器桥数；Kt为换流变压器变比；θ为控制角，整流器时为触发角，逆变器时为熄弧角；Xc为换相电抗；Is为换流变压器二次侧基波电流；K为计及换相重叠现象而引入的系数，在潮流计算中一般取0.995可达到足够精度；φ为换流器功率因数角；Ip为换流变压器一次侧基波电流。

2 无功优化数学模型

2.1 目标函数

电力系统无功优化的数学表达式为：

(7)

式中，minF(u,x)为目标函数，g(u,x)为等式约束，h(u,x)为不等式约束。

本文以计及直流输电线路网损的交直流系统总网损和电压偏移量的平方和为目标函数，由于直流输电线路损耗占额定输送容量的5%～10%，故只考虑直流系统的输电线路损耗。目标函数表示为：

F=min[facloss+fdcloss,fVD]；

(8)

(9)

fdcloss=Idc2R；

(10)

(11)

2.2 约束条件

2.2.1 等式约束

等式约束即电力系统的潮流约束功率平衡方程，对比于交流系统等式约束中包括交流节点的有功、无功功率平衡方程，交直流系统的等式约束包括交直流系统节点的有功功率约束方程和无功功率约束方程两部分，表达式为

(12)

(13)

式中：N为系统总节点数；Pli，Qli分别为负荷节点的有功和无功负荷功率；PGi，QGi分别为交流系统发电机节点的有功功率和无功功率出力；Pti(dc)，Qti(dc)分别为直流节点的有功和无功输入；QCi节点无功补偿容量；Gij，Bij，θij分别为节点i，j之间的电导、电纳和电压相差角。若节点为交流节点时ζ=0，为连接整流器的节点时ζ=1，为连接逆变器的节点时ζ=-1。

2.2.2 不等式约束

不等式约束可分为状态变量约束和控制变量约束。由于设备本身硬件设施的影响，控制变量需要维持在一定范围内，就构成了控制变量约束。控制变量即可以通过设备调节的变量，交流系统控制变量包括发电机有功、无功输出功率、发电机机端电压和变压器变比等。交直流系统控制变量除了交流系统控制变量外，还包括直流系统中换流器控制电压、控制电流、控制功率和控制角。状态变量约束即在系统稳定运行时，为了维持电压的稳定性，保证电能质量，需要对状态变量进行约束。交直流系统中控制变量包含发电机节点无功出力、负荷节点电压、支路功率以及换流变压器变比。

状态变量约束：

(14)

式中：QGo，QGo.max，QGo.min分别为发电机无功出力及其上下限；Ulp，Ulp.max，Ulp.min分别为负荷节点电压及其上下限；Qzp，Qzq.max，Qzq.min分别为支路无功功率及其上下限；Kds，Kds.max，Kds.min分别为换流变压器变比及其上下限。

控制变量约束：

(15)

式中：UGi，UGi.max，UGi.min分别为发电机端电压及其上下限；Ttk，Ttk.max，Ttk.min分别为可调变压器分接头位置及其上下限；QCj，QCj.max，QCj.min分别为无功补偿点无功补偿出力及其上下限；Udl，Idm，Pdn分别为换流器控制电压、控制电流和控制功率；cosθdr为换流器控制角的余弦值；Ng，Nt，Nc，Nd分别表示发电机节点总数、变压器可调分接头数、补偿节点数和网络节点数。

3 基于NSGAⅡ的多目标无功优化

通常对于多目标求解的一般思路是：用权重法或隶属度函数法将多目标转化为单目标问题求解。文献[8]对系统网损与电压质量加权，将双目标函数转化为单目标函数，并对权重取不同值，讨论了不同权重值对于优化结果的影响。但是由于不同目标函数值的量纲不同，这样做会使得无功优化结果受权重取值或者隶属度函数影响较大[9-10]。本文采用带精英策略的快速非支配排序遗传算法(non-dominated sorting genetic algorithm-II，NSGAⅡ)求解交直流系统多目标无功优化问题，不需要事先对目标函数权重值进行调整取值，可直接求得一系列pareto最优解，以供决策者根据不同的需求进行取值。

NSGAⅡ算法是基于遗传算法的多目标优化算法，在传统遗传算法加入快速非支配排序方法，并且在遗传过程中采用精英保留策略防止优良个体的丢失，求解得到多个pareto非劣解集的优化算法。交直流系统无功优化流程图如图2所示，其主要步骤如下：

(1)求解交直流系统网络方程，得到初始解UG(0)，Tt(0)，Qc(0)，Ud(0)，Id(0)，Pd(0)，cosθd(0)。

(2)输入系统原始参数：系统基准功率、系统节点数、发电机节点数、线路数以及节点、发电机、线路的具体参数。

节点参数：节点类型电压幅值、电压角度、输出有功、输出无功、输入有功、输入无功、并联电纳等参数。

发电机参数：发电机吸收的无功功率。

线路参数：线路首末端节点号、线路阻抗、线路电抗、线路电纳。

输入GA参数：每个种群的个体参数、每次迭代过程中杂交和变异的次数、判定是否杂交及变异的参数等。

输入变量：交流部分发电机电压、变压器变比、电容器投切容量，直流系统中控制电压、控制电流、控制功率和控制角余弦上下限输入。

(3)对交流离散变量编码和直流控制变量编码产生初始种群。

(4)采用交替迭代法进行潮流计算，并根据所得结果计算目标函数值，迭代次数k=1。

(5)快速非支配排序。快速非支配排序是依据分层处理原则，使种群不断向最优解逼近的一种快速排序方法。分层处理：首先将群体中非支配解集记为第一层分配F1，将其所有个体排序并从群体中除去；其次继续从找出剩余群体中的非支配解集记为第二层分配F2，将其全部个体排序并从群体中移出；依此类推，直至种类中的所有个体都被排序。并且在种群进化过程中，为保持种群的多样性，设计个体拥挤距离，选择拥挤距离较大的个体以维持种群多样性。

(6)选择、交叉、变异，本文选择操作选用轮赛制，即随机选择两个个体，选择非支配排序低、拥挤距离较大的个体。交叉操作采用实数编码的模拟二进制交叉(simulated binary crossover，SBX)。变异算子采用正态分布变异算子。

(7)精英保留策略。精英策略即保留父代优良个体直接进入子代，以防止优良个体的丢失。

(8)收敛判据：给定迭代次数，满足迭代次数则输出结果。不满足迭代条件重复步骤(4)。

(9)输出pareto最优解集。

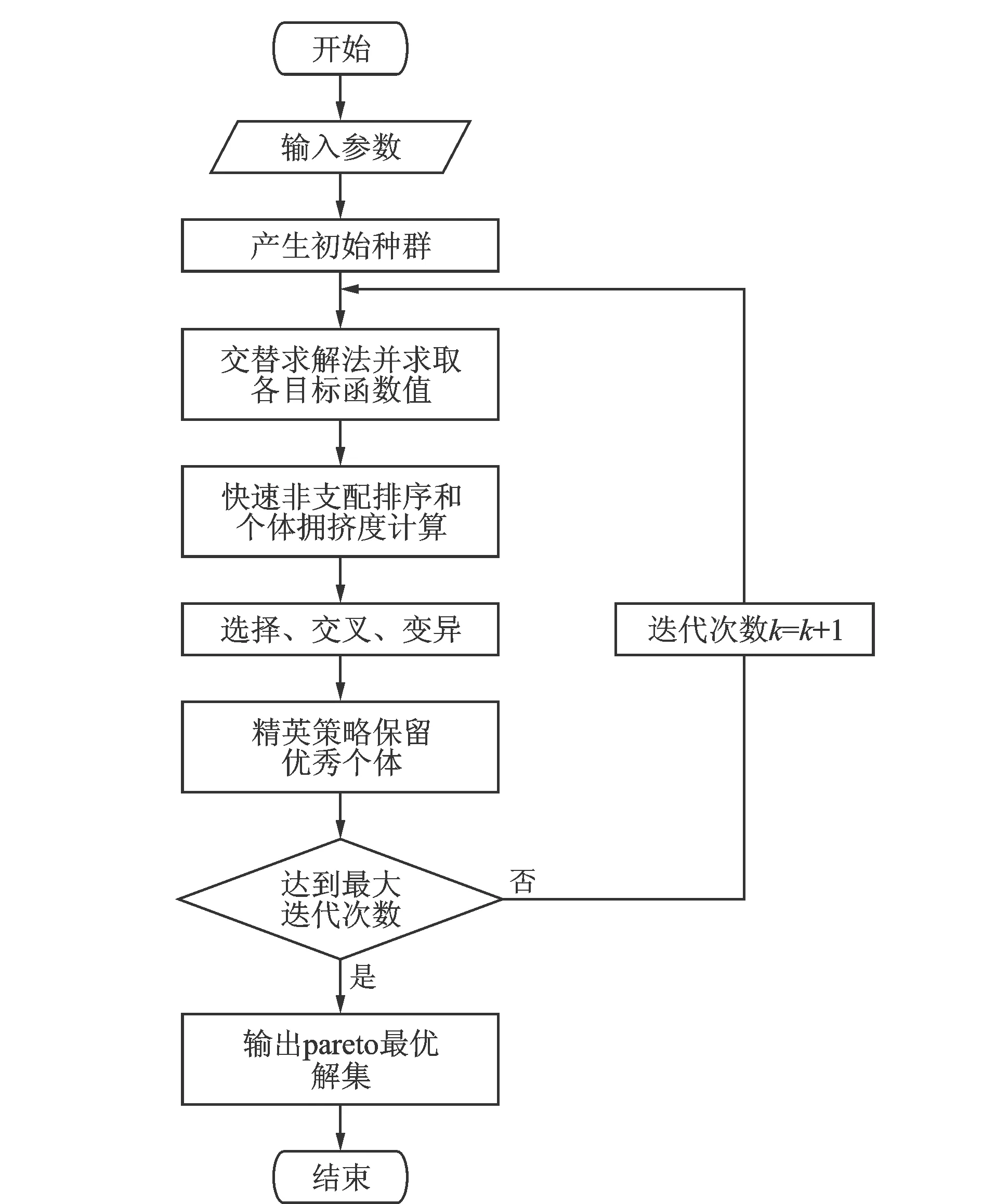
图2 基于NSGAⅡ算法的无功优化流程图Fig.2 Flow chart of reactive power optimization based on NSGAⅡ algorithm

4 算例与分析

4.1 测试系统参数

本文以文献[12]中IEEE 30节点系统为例，用计算结果验证本文算法可行性。系统数据见表1(其中，所有数据都是以100 MVA为基值功率的标幺值；发电机节点电压的上下限标幺值分别为1.1和0.9，其余节点电压的上下限标幺值分别为1.05和0.95)。

表1 直流节点的参数Tab.1 Parameters of DC Nodes

注：有功网损和电压偏移量均为标幺值。

4.2 测试结果

本文提出NSGAⅡ算法进行交直流系统无功优化，设置种群数为20，迭代次数为100，交叉率为0.9，变异率为0.1。控制方式采取整流侧定控制角，逆变侧定功率。所得pareto解集分布如图3。

图3 pareto最优解集Fig.3 Pareto optimal solution set

选取部分具有代表性的pareto最优解，见表2。

表2 部分pareto最优解Tab.2 Partial pareto optimal solutions

注：有功网损和电压偏移量均为标幺值。

由图3和表2可知，两个目标函数是相互矛盾的，当有功网损越小时，电压偏移量越大；电压偏移量越小时，有功网损越大。所以决策者根据实际需求选择最优解，若以有功网损最小为目标时，可选择编号2，若以节点电压偏移量最小为目标时，可选择编号1。

5 结 论

本文选取NSGAⅡ求解以交直流系统总网损和节点电压偏移量为目标函数的交直流系统无功优化问题。通过IEEE30节点系统算例验证了算法的有效性，优化结果表明两个目标函数不能同时达到最优，当有功网损最小时，电压偏移量最大。因此，当建立多个目标函数时，可通过NSGAⅡ求解出一系列pareto最优解集，便于决策者根据实际系统要求进行选择。