高抗挤套管磨损后的外压失效行为分析

张建兵，白 松，鞠录岩

(1.西安石油大学 机械工程学院，陕西 西安 710065； 2.陕西国防工业职业技术学院 数控工程学院，陕西 西安 710300)

引 言

随着深井、超深井钻井数量的增加，套管柱承受的载荷变得越来越复杂，油田对井筒完整性管理日益重视。当前，国内外的井筒完整性技术规范中均指出，在钻井设计、钻井过程及井下作业中应认真考虑磨损导致的套管强度降低。

套管的挤毁强度是其主要强度性能指标之一，套管的挤毁失效方式和行为受到其规格及钢级的影响，分为屈服挤毁、塑性挤毁、过渡挤毁及弹性挤毁。API标准[1]中已经明确了不同规格及钢级新套管的挤毁失效类型，但是对于磨损后的套管，由于其结构特征已经发生了变化，其失效行为与新套管不同，API未给出其挤毁强度的计算方法。

1992年，Yukihisa Kuriyama等[2]给出了Φ139.7 mmN80钢级磨损套管挤毁强度的实物实验值，认识到套管磨损后的剩余壁厚与初始壁厚的比值和剩余挤毁强度与原始挤毁强度的比值是一致的，即壁厚减小多少，挤毁强度就减少多少，指出磨损使套管挤毁强度降低的幅度小于管壁均匀减小后的理论计算值。Yukihisa Kuriyama等人的研究也是目前公开发表的仅有的磨损套管挤毁强度的较为系统的实验研究。2000年，高连新等[3]通过有限元方法研究了Φ244.48 mm×11.99 mm 110 ksi(758 kPa)钢级套管在25%和50%壁厚磨损率下的挤毁强度，认识到该套管挤毁强度与磨损量近似呈线性关系。2001年，覃成锦和高德利等[4]利用有限元方法研究了套管磨损缺陷长度对套管剩余挤毁强度的影响，以Φ127.0 mm×12.7 mm 110 ksi(758 kPa)钢级套管为例给出了计算数据。2007年，窦益华等[5]以磨损套管最薄处内壁环向应力达到管材屈服极限为判断条件,得到了磨损套管的剩余挤毁强度。2009年，王同涛和闫相祯等[6]以几种不同壁厚的Φ177.8 mm N80钢级套管为研究对象，建立了磨损套管的三维有限元模型,计算了不同磨损形态、磨损长度及深度对磨损后套管剩余强度的影响，认识到剩余挤毁强度与磨损长度成指数正比例关系，当磨损长度一定时,套管剩余挤毁强度随磨损深度的增加而线性降低。2010年，廖华林等[7]采用理论分析和有限元相结合的研究方法,给出了均布外载条件下磨损套管挤毁强度和抗内压强度的计算公式。2012年，梁尔国和李子丰等[8]利用有限元方法研究了Φ177.8 mm×11.51 mm 和Φ244.5 mm×11.99 mm110 ksi(758 kPa)钢级磨损套管的挤毁强度，认为磨损套管的挤毁为弹塑性挤毁方式的“三铰”失稳。2012年，Shen Zheng和Beck等[9]分析了高温井中温度对磨损套管引起的应力集中对套管挤毁强度的影响。2015年，Kumar和Samuel等[10]研究了最大磨损率达80%的N80和110 ksi(758 kPa)钢级套管的挤毁强度，指出在磨损率低于50%时，套管的挤毁强度加速下降，磨损率超过50%后下降趋势减缓。2018年，贾宗文[11]对弯曲井段磨损套管的挤毁强度进行了研究，认识到井眼弯曲会进一步降低磨损套管的挤毁强度。

总体来看，由于磨损套管挤毁失效力学行为及开展实物实验的复杂性，现有的理论研究工作还不够系统，实验研究工作仅限于20余年前N80钢级的Φ139.7 mm套管，对磨损套管挤毁失效行为变化的分析还基本未涉及。此外，我国西部深井、超深井当前广泛采用140钢级和110钢级的高挤毁强度套管，对该类套管磨损后挤毁强度的研究认识还不能有效指导当前深井、超深井井筒完整性管理。

本文对几种典型高抗挤套管磨损后的挤毁失效行为进行研究，重点探索套管磨损后其结构变化导致的管子挤毁失效行为变化，在关注外压载荷导致的套管内壁材料屈服的同时，探索磨损套管承受外压时的弹性失稳现象，并给出不同磨损率下的套管剩余挤毁强度值。

1 有限元模型

1.1 磨损套管参数及有限元基本假设

套管磨损形式考虑油田最主要的月牙形磨损，选取我国西部油田深井、超深井常用的3种典型高抗挤套管，其钢级与规格分别为：140 ksi(965 kPa)钢级Φ244.5 mm×11.99 mm套管、110 ksi(758 kPa)钢级Φ339.7 mm×12.19 mm套管、110 ksi(758 kPa)钢级Φ244.5 mm×11.99 mm套管。这3种套管在磨损前的挤毁失效形式分别为过渡挤毁、弹性挤毁和塑性挤毁，代表了3种典型的挤毁失效行为。按照套管壁磨损率分别为10%、20%、30%、40%、50%、60%、70%建立磨损套管几何模型。

计算采用Abaqus大型有限元分析软件，对有限元计算模型做出如下假设:

(1)磨损区贯通整段套管长度；

(2)套管受载后无相对运动；

(3)由于所分析的套管为高抗挤套管，忽略残余应力、轴向应力、椭圆度和壁厚不均度对套管强度的影响。

1.2 有限元基本方程

根据假设条件，采用二维平面应变计算模型，对磨损套管同时考虑弹性变形和塑性变形，在弹性区采用Hook定律，在塑性区采用Von Mises屈服准则以及Prandtl-Reuss塑性流动增量理论。考虑由于大位移对单元形状及有限元结果的影响，相对于变形的几何位置列出平衡方程，应力-应变曲线采用真实应力-对数应变曲线。分析过程中考虑材料非线性和几何非线性。

在Updata Lagrangian方法中，虚功方程表示为：

(1)

式中：Sij为对称二阶Piola-Kirchoff应力张量；Eij为Green-Lagrangian应变张量；bi0、ti0为体积力、面力；ηi为虚位移。

将应力与共轭应变带入上述虚功方程，即可得到单元的平衡方程式：

{K1+K2}δ=F-R。

(2)

式中：K1,K2分别为材料刚度矩阵、几何刚度矩阵；F,R分别为内力、外力。

在磨损套管强度非线性分析中，K1和K2已经不是常数矩阵，在它的各个元素中还包含节点的位移分量，所以由各个单元的平衡方程式集成的整个结构的有限元方程是一个非线性代数方程组，用牛顿-拉斐逊方程求解。分析的问题属于大应变问题，求解时增量平衡方程式采用Updata Lagrange 公式。

1.3 材料参数

对110 ksi(758 kPa)和140 ksi(965 kPa)两种钢级材料的最小屈服强度分别取758 MPa和965 MPa，泊松比取0.3，杨氏模量取2.1×105MPa，所分析的问题属于非线性弹塑性问题，对材料采用线性等向强化模型。

1.4 模型网格划分

采用中性轴法划分网格，单元类型为CPS4R，该单元类型采用沙漏控制，收敛性好，缩减积分计算使计算的速度更快。

1.5 边界条件

如图1所示，在y=0边界上施加y向固定约束。为避免节点位移发生漂移，将物理坐标y值最大的节点施加x向固定约束，磨损最深处在x=0的正方向。

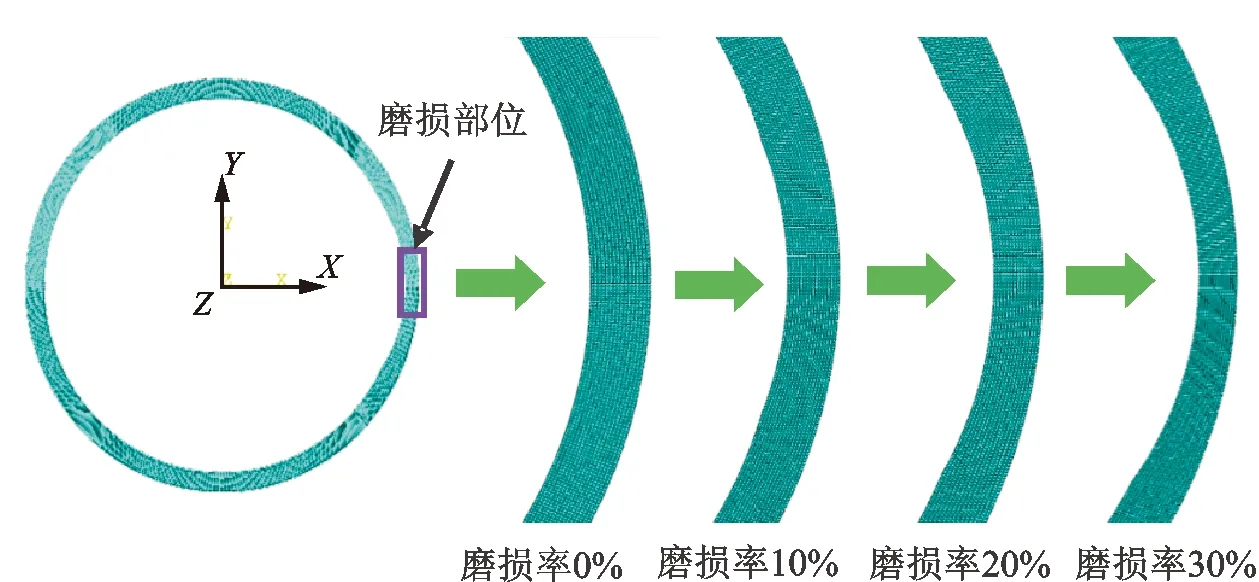
图1 磨损套管模型Fig.1 Worn casing model

1.6 磨损套管挤毁失效判据

套管的挤毁失效方式受其规格及钢级直接影响。套管管壁出现月牙形磨损沟槽后，套管原有的结构特征已经被改变，此时，无法保证其失效行为与新套管相同，不宜再按照新套管的失效形式采用单一挤毁失效判据。这里对每种套管在不同磨损率下同时采用塑性及弹性挤毁失效判据进行判断，以先发生的失效作为套管的挤毁失效形式，对应的外压载荷作为套管的挤毁强度值。

(1)塑性挤毁失效准则

改变套管外压载荷p，当套管上最大Von Mises等效应力达到材料的屈服强度时，套管进入塑性变形阶段，此时得到的外压载荷p即为套管的挤毁强度。当外载p持续增加时，使套管材料达到抗拉伸极限时，套管整体出现塑性变形的比重更大，套管发生挤毁。

(2)弹性失稳挤毁失效准则

套管在外压作用下，材料弹性变形阶段外壁应变与外压力呈线性关系，各点的应变直线上升，外压力继续增大，在磨损部位产生应力集中，当外载超过某一临界值时，变形明显增加，套管因结构失稳而失效，设定此载荷为套管弹性失稳挤毁强度。选用载荷-位移法作为判断套管失效的依据，具体做法是：对每一载荷步的位移进行对比分析，当后一载荷产生的位移与前一载荷产生的位移之比大于20时,即认为套管发生弹性失稳失效。也就是说，此时施加一微小载荷，套管就产生一个位移突变，表示套管结构已经发生突然失稳。

2 塑性挤毁失效套管磨损后的强度

110 ksi(758 kPa)钢级的Φ244.5 mm×11.99 mm新套管的挤毁类型为塑性挤毁，即当套管承受外压时，管壁中的应力随着载荷的增加而逐渐增加，其最大应力点出现在内管壁上，随着载荷增加，内管壁会逐渐屈服。

套管磨损后，同时采用塑性挤毁判据和弹性失稳判据分析其挤毁行为。对于弹性失稳判据，在套管同一平面的内外壁上选取6个节点作为关键分析点，如图2所示。

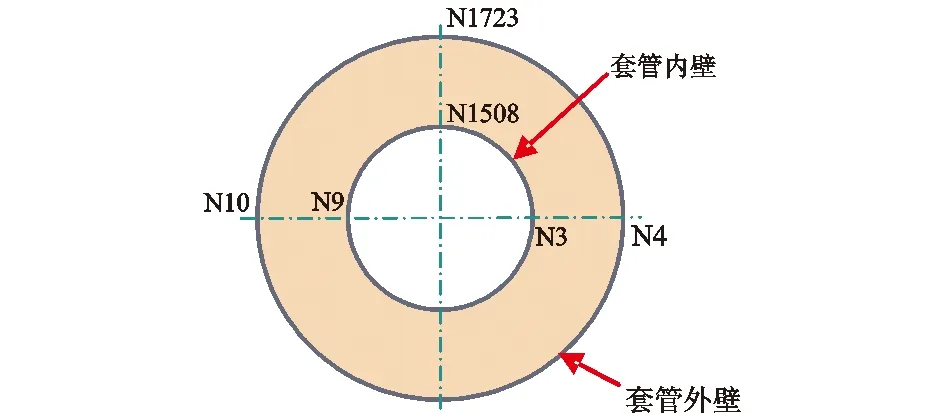
图2 套管有限元计算模型关键节点示意图Fig.2 Schematic diagram of key nodes for finite element calculation of casing

计算得到的不同磨损率下套管挤毁强度值及其变化如图3所示。由于套管是按照理想尺寸建模的高抗挤套管，所以图3中新套管的强度值高于API 5C2[12]给出的普通套管的值。

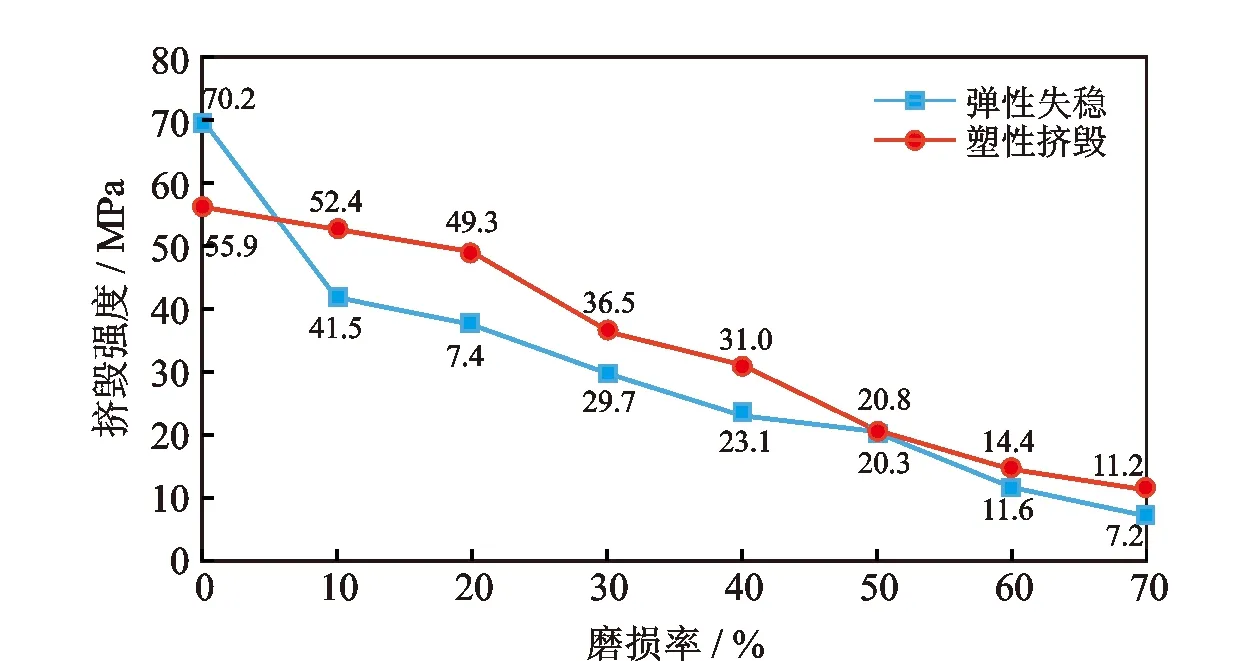
图3 Φ244.5 mm×11.99 mm 110 ksi(758 kPa)套管在不同磨损率下的挤毁强度Fig.3 Collapse strength of casing Φ244.5 mm×11.99 mm 110ksi(758 kPa) under different wear rate

由图3可见，该套管在磨损后分别依据塑性挤毁和弹性失稳计算得到的挤毁强度值不一致，按照先触发的失效判据的计算值为套管挤毁值的原则，该套管在磨损后挤毁失效类型发生了变化，而且表现出与磨损率的相关性。

当磨损率大于10%时，套管先发生弹性失稳而挤毁。此时，随着外挤载荷逐渐增大，套管壁的应力逐渐增加，靠近内壁处的应力大于其余部位，并在月牙形磨损部位出现应力集中。但尚未超过材料的屈服极限，到某一外压载荷时，套管突然出现失稳而挤毁。磨损率为30%时，套管上6个关键节点的位移随载荷增加的变化曲线如图4所示。从图4中可见，当载荷超过29.7 MPa时，6个节点的位移都发生了突变，触发了弹性失稳失效判据。此时套管的应力云图如图5所示，套管内壁应力最大值为703 MPa，尚未达到材料的屈服点。若此时按照套管塑性屈服准则继续增加载荷计算套管挤毁强度已经没有意义，且会高估套管的挤毁强度。根据套管塑性挤毁时的应力云图，对应的套管外挤载荷为36.5 MPa，比套管发生弹性失稳挤毁的外挤载荷高6.8 MPa，套管的挤毁强度被高估。

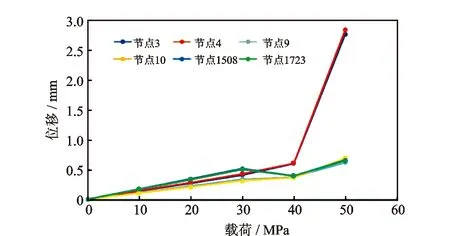
图4 磨损率为30%的110 ksi(758 kPa)钢级Φ244.5 mm×11.99 mm 套管在不同外压载荷下的关键节点位移Fig.4 Displacement of key nodes of casing Φ244.5 mm×11.99 mm 110ksi(758 kPa) with wear rate of 30% under different external pressure loads

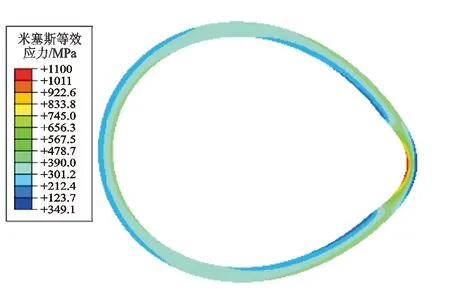
图5 磨损率为30%的110 ksi(758 kPa)钢级Φ244.5 mm×11.99 mm 套管外压失稳时的应力云图Fig.5 Stress nephogram of casing Φ244.5 mm×11.99 mm 110ksi(758 kPa) with wear rate of 30% in external pressure instability state

这些数据印证了本文对于磨损套管失效类型相比原套管发生变化的推断，也证明了本文对于套管挤毁失效判据的设定是正确的。

3 过渡挤毁失效套管磨损后的强度

Φ244.5 mm×11.99 mm140 ksi(965 kPa)钢级新套管的挤毁失效类型为过渡挤毁，按照与110 ksi(758 kPa)钢级Φ244.5 mm×11.99 mm磨损套管相同的分析方法对该套管的挤毁强度进行分析，结果如图6所示。

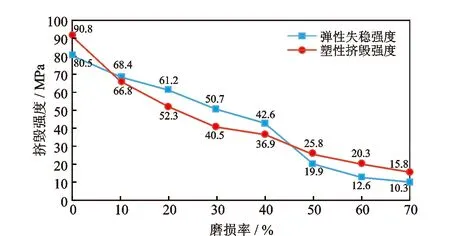
图6 Φ244.5 mm×11.99 mm140 ksi(965 kPa)套管在不同磨损率下的挤毁强度Fig.6 Collapse strength of casing Φ244.5 mm×11.99 mm 140ksi(965 kPa) under different wear rate

从图6可以看出，Φ244.5 mm×11.99 mm 140 ksi(965 kPa)钢级磨损套管的挤毁失效行为与Φ244.5 mm×11.99 mm110 ksi(758 kPa)套管不同。本来为过渡挤毁的套管在磨损后其挤毁失效行为表现出了明显的塑性或弹性失稳特征，当磨损率≤50%时，套管的挤毁失效类型为塑性挤毁，当磨损率>50%时，其挤毁失效类型转变为弹性失稳。

4 弹性挤毁套管磨损后的强度

Φ339.7 mm×12.19 mm110 ksi(758 kPa)新套管的挤毁失效类型为弹性失稳，对该套管磨损后的挤毁强度进行了分析，不同磨损率下套管的挤毁强度如图7所示。

图7 Φ339.7 mm×12.19 mm110 ksi(758 kPa)套管在不同磨损率下的挤毁强度Fig.7 Collapse strength of casing Φ339.7 mm×12.19 mm110ksi (758 kPa) under different wear rate

从图7可以看出，该套管磨损后的挤毁失效行为与前面分析的两种套管都不同,磨损后挤毁方式没有发生变化，依然表现为弹性失稳，有限元分析数据表明其磨损部位的应力集中显著，这说明弹性失稳的套管在管壁磨损后结构变得更加不稳定，但其强度下降幅度与Φ244.5 mm×11.99 mm110 ksi(758 kPa)套管和Φ244.5 mm×11.99 mm140 ksi(965 kPa)套管相当。

5 套管挤毁强度与磨损率的关系

图8为本文分析的3种套管的磨损率与挤毁强度下降幅度关系曲线。从图8可以看出，无论属于何种挤毁方式，3种套管的挤毁强度都随着磨损率的增加而下降，挤毁强度与磨损率近似呈线性关系。对比不同磨损率套管的挤毁强度可以发现，在磨损率低于40%时，弹性失稳的套管挤毁强度下降幅度要高于塑性挤毁和过渡挤毁的套管。对Φ244.5 mm×11.99 mm140 ksi(965 kPa)钢级套管，在磨损率低于50%时，套管挤毁强度幅度基本上随着磨损率的增加而线性增加，当磨损率高于50%时，挤毁强度出现了快速下降，这是磨损率高于50%时套管的挤毁失效类型由塑性挤毁转变为弹性失稳导致的。对Φ339.7 mm×12.19 mm 110 ksi(758 kPa)套管，在磨损率低于30%时，套管的挤毁强度下降迅速，磨损率超过40%后，挤毁强度的下降速度减慢。

图8 3种套管磨损率与挤毁强度下降幅度的关系曲线Fig.8 Relationships between collapse strength decrease and wear rate of three casings

6 结 论

(1)Φ339.7 mm×12.19 mm110 ksi(758 kPa)套管、Φ244.5 mm×11.99 mm110 ksi(758 kPa)套管、Φ244.5 mm×11.99 mm140 ksi(965 kPa)套管在磨损后的挤毁失效行为与新套管相比发生了变化，在计算磨损套管的挤毁强度时，不能再采用原始新套管的失效判据，应同时按照塑性屈服和弹性失稳条件考虑。

(2)磨损套管的挤毁失效类型与套管的磨损率密切相关。壁厚磨损率50%是磨损套管挤毁失效类型转变的分界点，套管磨损后其结构稳定性降低，更易于发生弹性失稳，在计算磨损套管的挤毁强度时应加以注意。

(3)原本为塑性挤毁的Φ244.5 mm×11.99 mm110 ksi(758 kPa)套管，在磨损后转变为以弹性失稳为主，即套管在承受足够大的外压时没有发生内壁屈服时就已经失去结构稳定性而失效。

(4)原本为过渡挤毁的Φ244.5 mm×11.99 mm140 ksi(965 kPa)套管，当磨损率≤50%时，挤毁失效类型为塑性挤毁，当磨损率>50%时，其挤毁失效类型转变为弹性失稳。

(5)原本为弹性挤毁的Φ339.7 mm×12.19 mm110 ksi(758 kPa)套管在磨损后依然为弹性挤毁，磨损加剧了其结构的不稳定，磨损后其挤毁强度下降，下降幅度与Φ244.5 mm×11.99 mm110 ksi(758 kPa)套管和Φ244.5 mm×11.99 mm140 ksi(965 kPa)套管相当。