一种改进的海量信息分类算法
2019-10-11戴立平谭正华张进修张又文
戴立平,谭正华,张进修,张又文
(湘潭大学 信息工程学院,湖南 湘潭 411105)
0 引 言
信息的分类常常表现为树状结构,在实际应用中,一般用Table表表示,而快速生成资讯的所在路径和实现某个分类的增删,是研究的关键和热点。
通常情况下,在数据库中对每一个分类新建一个数据表,增加一个分类就增加一张表。当需要将该分类的信息显示时,通过查找找到该分类的数据表,但操纵数据表比操纵数据表中的记录困难得多,因此数据表的多少直接关系到查询的效率。
Hao Chunmei等[1]提取信息属性的特征,根据特征建立优化信息分类模型,实现高效的信息分类,为快速查询搜索目标提供支持;张成刚等[2]提出利用降噪编码自适应神经网络对采集的信息进行降噪处理并利用分类规则对海量信息进行智能分类,但该方法计算过程较为复杂,且分类耗时较长;曾劲松等[3]提出基于冲突博弈算法的海量信息智能分类,通过提取信息特征,确定信息分类策略。
以上方法难以很好地解决信息分类查询的效率问题,因此文中提出一种海量信息分类算法,包括信息分类编码和算法API,实现了分类处理的各种应用需求,进一步提高了查询搜索效率。
1 普通的信息分类方法
在信息分类中,树形结构的每一个节点表示一个分类[4],定义一个Catalog表,分类节点中只保留一个Name信息。添加一个CatalogId自增主键作为节点编号。为了将该树形结构更为准确地描述出来,在节点中再增加一个字段,将这个字段命名为FatherID。如果节点ID2是ID1的子节点,那么说明这个分类是该分类的子节点,即ID1就是ID2的FatherID。约定0为第一层父类编码,作为一个在数据库中无任何记录的虚拟分类。
上面定义的Catalog表可以较为轻松地恢复出一棵分类树。当需要查找该父类的下级分类时,只需要使用SQL语句选择表中FatherID=FID的部分。通过调用寻找分类下子分类的GetChildren函数,然后把该子分类的CatalogId主键作为下一个分类的FatherID,通过递归调用得到该分类下的所有子分类[5]。
假设要搜索某一个大类下的所有资讯,该大类下有较多的分类层级,而且资讯靠近根分类[6]。不仅需要搜索出大分类的信息,也要将子分类的信息搜索出来。一般情况下,将递归调用GetChildren函数查找得到所有分类及其子分类,通过获得的分类ID,调用GetProduct函数查询该分类对应的产品。比如一个分类下其子分类,子子分类有20个,那么函数调用次数将达到20次,其查询效率较为低下。
2 分类编码的优化设计
2.1 文档分类存储表结构
在设计中,主要使用了两张表(见图1)。
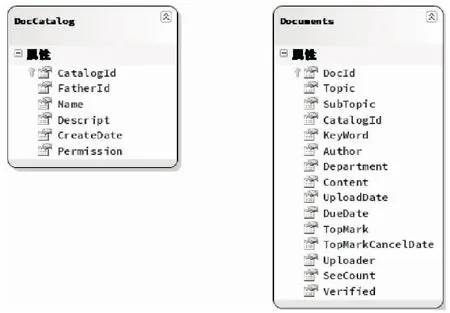
图1 数据结构表
一张为信息分类基础DocCatalog表,主要用来存储文档的分类信息,里面主要有4个关键字段。其中CatalogId为分类节点ID,FatherId为分类父节点ID,Name为分类名称;另一张表为Documents表,主要用来存储文档数据,关键字段:DocId为文档ID,CatalogId为文档所属分类ID,这个字段作为外键与DocCatalog表中的主键CatalogId具有约束关系[7]。
2.2 信息分类编码结构
将DocCatalog表中的主键CatalogId定义为bigint数据类型[8],大小为8个字节,存储64位二进制。如图2所示,将64长度从右到左分割成9段,每一段为7位,最左边剩余的一位废弃不用,可以获得ABC至I个完整的二进制段,规定当7位编码全为0时不表示任何分类编码。A段位第一层分类编码,每一层分类的编码最小值是从0000001开始表示的。全零的段值不表示分类编码。当创建第一层的第一个分类时,就用二进制0000001表示,如果该层级需要创建第二个分类,分类编码就为0000010,本层级的最后一个分类用编码1111111表示。

图2 信息分类编码
设计的分类编码结构,对于每一个层级,可以有27=128个编码,除去全为0的编码,每层级可以表示127个分类。对于64位编码,一共有1279个分类。这对于企业信息分类已经足够使用[9]。
当A段分类下无子分类的时候,那么其他段位值全为0。当A段一层分类有子分类时,则第二层的子分类编码从0000001开始。从A至I段的编码总是从0000001开始到1111111结束。如图3所示,这是一个多层分类实例。
假如给定一个分类,其十进制的编码值为4210818,将其转换成二进制编码:1000000100000010000010,按从右到左7位为一段,不足7位补0,依次为:0000010 0000001 0000001 0000001,一共分割成了4段,该分类为第四层子分类。可以得到其上父节点的编码为0000001 0000001 0000001,十进制编码值为16 513;第二层级的编码为0000001 0000001,十进制编码值是129;第一层级的分类编码为0000001,十进制编码值是1。对于分类的分类层级和其所有的分类路径,只需要给定该分类的编码值,就能完整地分析出来[10]。
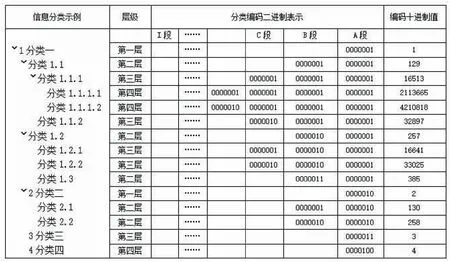
图3 分类编码二进制位
3 算法实现
基于此分类编码,设计了一套使用简单、效率高效的算法。该算法基于微软LINQ技术进行实现[11]。在信息分类的程序集中定义一个CatalogTreeBase信息分类基础类,另外还定义了几个关键基础信息。
(1)MaxLevels,这是信息分类的总级数,由前面分类级数可知,其值为9,是一个常量。
(2)LevelLengh,这是分类编码的二进制长度,也是一个常量,其值为7。
(3)分类K码,这是算法中的关键信息,其值的定义为2LevelLengh。这是一个永恒不变的常量,由于上述LevelLength值为7,所以K值为128。
(4)LevelGrade分类编码层,在计算机中,移位操作是非常便捷高效的。通过对编码值的右移操作,将编码值进行分割,那么LevelGrade值就是其分割后的段数。
(5)父类截取码,在程序中用LevelK表示。这是一个变量,用于将分类编码与父类截取码进行运算后取得上一级的父类编码,算法定义为KLevelGrade。按照定义,对于第一层的LeveK值即为K码,第二层为K2,依次类推,可以看出当父节点相同时,其他兄弟分类具有相同的Level值。
在实际应用中,如果给出一个分类编码的Id[12],对于其父类的编码值只需要用分类Id的编码对上层的LevelK进行取模运算:FatherId=Id%GetFather-LevelK(Id)。当输入分类编码值Id,即可求出上一级的LevelK值。在项目的实际应用中,为了能够便于随时进行调用,定义:public static ulong GetFatherId(ulong Id)。这是一个计算父节点编码的函数。而对于海量信息分类的解决方案,传统方法是通过对数据库进行迭代查询操作,改进的分类算法只需要进行取模运算,即能快速地得到分类的父分类编码[13]。
对于获取某一分类下的直接下一级子分类,或者根据指定的分类编码获取下级的所有分类,在信息方案中,普通方法是采用迭代循环的方式,调用查找子类的方法,来找到所有的子分类。对于优化的分类编码,所有子分类编码中就包括了父节点的编码。在运算的时候,如果子分类的编码中能够解析出父类编码,那么该子类就能够被视为找到。LINQ的子类查询语句如下:
Public IQueryable
{
longlevelK=GetLevelK(id);
var query=from u dbContext.Catalog where u.CatalogId % levelK==id select u;
return query.AsQueryable
}
在上述语句中,对于父分类编码的获得,在查询时只需要分类编码对父分类levelK进行取模操作,u.catalogId%levelK==id。在图3中,对于3层级分类1.2.1,其分类编码值为16 641,父类的levelK为K2=16 384,对其取模得到16 641%16 384=257,而二层级分类1.2的编码值就是257,可以判定为该分类是分类1.2的子分类,同理可判定1.2.2也是分类1.2的子分类。如果需要查找一个指定分类的下层级子分类,使用LINQ查询时,增加一个判定条件,下层级的比父分类层级大1,其代码如下[14]:
Public IQueryable
{
int levelGrade=GetLevelGrade(id)+long levelK=GetLeveelK(id);
var query=from u dbContext.Catalog where u.CatalogId % levelK select u;
return query.AsQueryable
}
由于LINQ语句不能直接去调用外部函数GetLevelGrade(),这里使用的是伪代码,用来判定父分类比子分类的层级高1级。
在实际项目中,经常需要恢复出目录树。采用递归的方式,调用前面定义的GetChildrenCatalog()函数,就能较为简便轻松地实现完整的信息分类树。
4 算法测试
为了测试改进的海量信息分类查询方法和普通迭代信息分类方法的效率差异,将在不同测试条件下进行算法的性能测试,其测试环境相同。测试主要采用的实例为生成分类树。
测试一:查找的分类指定,其Id为1,分类层级为3,每层级有8个子分类。
测试二:查找的分类指定,其Id为1,分类层级为4,每层级有8个子分类。
测试三:查找的分类指定,Id也为1,分类层级为4,每层级有20个子分类。
图4和图5为测试用时结果比对,可以得出以下几点结论:
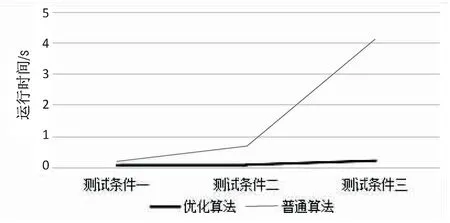
图4 运行耗时结果比对
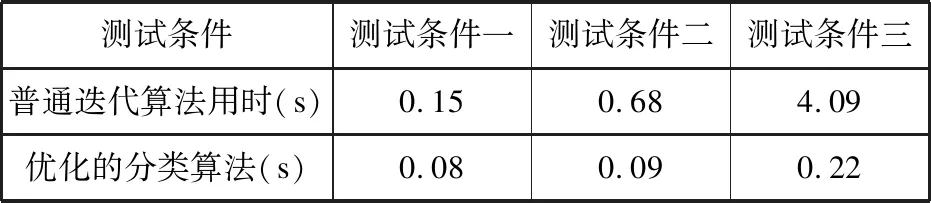
测试条件测试条件一测试条件二测试条件三普通迭代算法用时(s)0.150.684.09优化的分类算法(s)0.080.090.22
图5 测试用时
(1)当分类的层级较少且分类数目不多时,改进的海量信息分类算法和普通的迭代算法在耗时时间上差异较小,但改进的分类算法性能上较优。
(2)在分类层级增加,而且分类总数也增加的情况下,改进的分类算法要比普通的迭代算法少一个数量级的时间。
(3)当分类层级和分类的总数大量增加时,改进的分类算法在耗时上差异较小,在增长速率上更加优于普通的迭代算法。
5 结束语
提出了一种查询、检索海量信息的分类算法,其特点如下:优化编码设计,编码值包含了信息分类的层次结构,能提供最大9层级约8.59×1018个分类,保证了信息分类结构的完整。通过基于微软的LINQ技术设计了一套简单、高效的算法,借助计算机的高速运算能力,能快速解析出信息分类的结构层次与分类编码。优化的算法为海量信息分类提供了参考,有利于提高信息数据检索的效率。
