例谈Simulink在物理教学中的应用
2019-10-10闫小军陈夏玲
闫小军 陈夏玲


摘 要 通过对弹簧振子等运动规律的仿真研究,详细介绍Simulink仿真工具建立模型和仿真的方法,充分体现了Simulink
仿真工具在物理教学中的优越性,利用它能够有效突破物理的教学难点,提高课堂教学效率。
关键词 Simulink;物理;MATLAB
中图分类号:G633.7 文献标识码:B
文章编号:1671-489X(2019)03-0048-04
1 前言
Simulink是矩阵实验室MATLAB最重要的组件之一,是一种可视化建模和仿真工具,提供了一个动态系统建模、仿真和综合分析的集成环境。它采用模块组合的方法,使用户快速、准确地创建动态系统的计算机模型,使得建模仿真如同搭建积木一样简单,省去许多重复的代码编写工作。
在物理教学过程中常会遇到一些复杂的物理规律和运动过程,这些运动规律的推导与计算往往比较烦琐、抽象,计算的结果也难以直观理解。可以通过Simulink仿真功能,将复杂、抽象的物理过程直观形象地展现给学生,从而帮助学生深入理解,达到高效课堂的目的。本文通过实例,呈现Simulink仿真工具在物理教学中的应用,希望能够起到抛砖引玉的作用。
2 弹簧振子运动过程仿真
如图1所示,弹簧振子的质量为m,弹簧劲度系数为k,振子还受到与速度大小成正比、方向相反的空气阻力,阻尼系数为b。根据牛顿第二定律,振子运动的微分方程为:
mx″+bx′+kx=0
变形整理为:
启动Simulink工具 打开MATLAB软件,在MATLAB运行环境中点击Start→Simulink→Library Browser。
Simulink模型窗口的建立 选中Simulink Library Browser菜单中的File→New→Model菜单项后,即打开一个新的空白模型窗口。
Simulink模型的建立 在模块库浏览器Simulink Li-brary Browser中找到所需模块,用鼠标左键点取求和模块(Add)、增益模块(Gain)、积分模块(Integrator)、信号通路模块(Mux)、示波器模块(Scope),并将模块拖到模型窗口中,用鼠标左键在模块间建立连接线,即可完成模块的建立。在信号通路模块的属性窗口中设置输入个数为7,允许示波器同时接收7路信号,图2为其中的一路信号,再复制6组分别接入信号通路模块其他输入端口。图2为位移曲线仿真模型,图3为速度曲线仿真模型,其中求和模块(Add)输出量为加速度x″,第一个积分模块输出量为速度x′,第二个积分模块输出量为位移x。
设置模块属性和仿真参数 在所建立的模型窗口中,选中相应的模块,双击模块,打开该模块的参数设置对话框进行相应设置。第一个积分模块设置初速度为0,第二个积分模块设置初位移为4,取质量m=2 kg,劲度系数k=1 N/m,
阻尼系数b分别为0、0.4、1、2、2.4、3、4,则第一个增益模块位移系数k/m设置为-0.5,第二个增益模块速度系数b/m分别设置为0、-0.2、-0.5、-1、-1.2、-1.5,-2。
模型的运行仿真 点击工具栏中的Start Simulink按钮运行,双击Scope模块,观察仿真结果。图4为弹簧振子运动的位移曲线,图5为弹簧振子运动的速度曲线。
仿真结果分析 从位移曲线可以直观地看出:阻尼振动的振幅随时间呈指数递减,阻尼系数越大,振动衰减越快,且周期越长,频率越小。从速度曲线可以直观地看出:阻尼振动存在一个临界阻尼系数,当阻尼系数大于或等于临界阻尼系数时,速度大小会逐渐减小为零;当阻尼系数小于临界阻尼系数时,物体速度也会作周期性变化;在不计阻尼的情况下,即b=0时,物体作简谐振动。
3 等量同种电荷连线的中垂线上电场强度的变化规律仿真
电场强度的数学表达式 如图6所示,设电荷的半径为r,Oxy平面上,在点(-a,0)和(a,0)处分别有一正电荷q,则在两个电荷连线的中垂线上场点P(0,y)处的电场强度E为:
Simulink模型的建立及模块参数的设置 建立的Simu-
link模型如图7所示,取k=9×109,q=1.6×10-19 C,a=5.6×
10-15 m,双击自定义模块Fcn,输入场强E与位置关系y的表达式:
2*(9e+9)*(1.6e-19)*u/sqrt((u*u+(5.6e-15)^2)^3)
模型的运行仿真 从图8中可以直观地看出,在两个电荷连线中点处,即y=0时,电场强度为零,在中垂线上电场强度先增大后减小,存在一个最大值。利用MATLAB的放大功能,对图8进行放大得到图9,可以直观地看到当y=3.96×10-15 m时有最大值,Emax=3.535×1019 N/C。
4 带电粒子在两个等量同种电荷连线的中垂线上运动规律的仿真
带电粒子运动的微分方程 如图6所示,将电量为-q0,质量为m的带电粒子,在两电荷连线的中垂线上某一点(0,y)自由释放,由牛顿第二定律得:
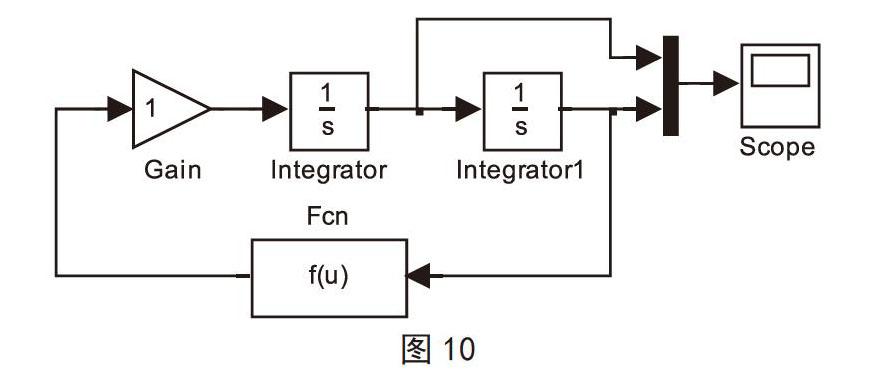
Simulink模型的建立及模块参数的设置 建立的Simu-link模型如图10所示,取k=1,q=1,q0=1,a=1,双击自定义模块Fcn,输入化简后的表达式-2u/sqrt((u^2+1)^3),
第一积分模块初速度设置为0,第二积分模块初位移取不同值进行仿真。
模型的运行仿真 从图11和图12中可以看出,带电粒子的运动规律与释放粒子的初始位置有关。图11是带电粒子从小于电场强度最大值的位置由静止释放的运动图像,粒子先做加速度逐渐减小的加速直线运动,到达平衡位置时加速度为零,速度最大;然后做加速度增大的减速直线运动,直到速度减小为零,完成半个周期的运动。图12是帶电粒子从大于电场强度最大值的位置由静止释放的运动图像,运动规律相对复杂,带电粒子先做加速度逐渐增大的加速直线运动,加速度达到最大,再做加速度逐渐减小的加速直线运动,到达平衡位置时加速度减为零,速度达到最大;然后再做加速度逐渐增大的减速直线运动,加速度达到最大,再做加速度减小的减速直线运动,最后速度减为零,完成半个周期的运动。
5 结语
通过MATLAB/Simulink工具仿真,研究了弹簧振子的运动规律、等量同种电荷中垂线上电场强度的变化以及带电粒子的运动规律,不难看出MATLAB/Simulink仿真工具在物理教学中的优越性,其避免了大量繁杂的数学推导和重复的计算机程序编写,极大地提高了教师的备课效率,且仿真结果能真实地反映物理规律的本质,有效突破了物理教学的难点,提高了课堂效率。■
参考文献
[1]刘浩,韩晶.Matlab R2014a完全自学一本通[M].北京:电子工业出版社,2015.
[2]杨永艳.SIMULINK在简谐运动图像教学中的应用[J].技术物理教学,2011,19(3):69-70.
[3]朱国强.求解物理方程:Matlab软件在物理教学中的应用之一[J].物理通报,2014(5):94-98.
[4]黎雪,罗春润,罗志荣.MATLAB在中学物理最值问题上的应用[J].广西物理,2015,36(2):35-38.
