基于函数cot(xα)变换的傅立叶级数在大坝变形数据分析中的应用
2019-10-10王江荣王庆岭
王江荣,王庆岭
(兰州石化职业技术学院信息处理与控制工程学院,甘肃 兰州 730060)
大坝在建设期和运营期都会因地质构造、周围环境、气温变化、施工技术、坝体自重及水力作用等发生变形,科学、合理地预测大坝变形对确保大坝安全具有重要意义。受监测条件的影响,大坝的变形监测数据列往往含噪声且具有波动性大、规律性和平稳性较差的特点,针对这类变形监测数据列建模,已有研究分别采用了经验模态分解技术[1]和B样条函数[2],这两种建模方法均取得了理想的预测效果,但也存在建模过程复杂等问题。本文在已有研究成果的基础上,提出了一种基于函数cot(x2)变换的傅立叶级数建模方法,利用该建模方法得到的大坝变形预测模型具有很强的数据适应能力和外推能力,只需少量级数项就能达到理想的预测效果,对于其中的模型系数及相关参数可采用遗传算法估算。实证分析表明利用该建模方法所建立的大坝变形预测模型具有很高的预测精度,可应用于工程实践。
1 函数cot(x2)变换及傅立叶级数建模流程
1.1 函数cot(x2)变换
1.2 傅里叶级数
若函数f(t)在闭区间[-l,l]上连续或仅有有限个第一类间断点,则函数f(t)可利用傅立叶级数来表示[5],即:
(1)



1.3 基于函数cot(x2)变换的傅立叶级数建模流程
本文提出的基于函数cot(x2)变换的傅立叶级数建模流程,详见图1。

图1 基于函数cot(x2)变换的傅立叶级数建模流程
2 工程实例应用与分析
某大坝变形监测数据[7](观测时间间隔相同)见表 1,本文利用前32期的大坝变形监测数据建模,利用后4期即第33、34、35、36期的大坝变形监测数据对模型进行检验。

表1 某大坝变形监测数据
某大坝前32期的切向位移原始监测数据点分布,见图2。

图2 某大坝前32期的切向位移原始监测数据点分布
由图2可见,因受工程地质构造、土壤物理性质、大气温度、水文、建筑物承受荷载、建筑物内部结构、所用材料及施工质量等随机性因素的影响[8-10],该大坝变形原始监测数据列的波动性较大,呈现部落或族状,光滑度及规律性均较差,因大坝变形是一个渐变的过程,所以描述这类数据点的函数通常是连续的或存在第一类间断点,故可利用傅立叶级数来逼近这类数据点。需要指出的是,数据的光滑度越高,利用傅立叶级数逼近的效果就越好,故将原始监测数据列作函数cot(x2)变换,以提高数据列的光滑度,具体过程如下:
(1) 对大坝变形原始监测数据列进行标准化处理:对该大坝前32期切向位移原始监测数据做如下标准化处理:
(2)



(3)
式中:t为监测次数(次),且t=1,2,…,32,以下相同。
本文采用遗传算法对模型系数及相关参数进行估算。定义目标函数(适应度函数)如下:
(4)
设n=3,打开Matlab遗传算法工具箱GAOT界面GUI[11],在Fitness function中输入@finess(目标函数的Matlab程序名,程序在此略),在Number of Variables中输入8,在下边界lower中输入-2*ones(1,8),在上边界Upper中输入2*ones(1,8),执行Start命令,经79次迭代(迭代过程见图3),输出的目标函数最优值为0.000 598 781,输出的模型系数及相关参数值如下:

图3 适应度函数变化曲线

从傅立叶级数提取的模型为
S3(t)=0.698 8-0.225 2cos0.073 7t-0.445 2sin0.073 7t-0.208 5cos0.147 4t+0.264 9sin0.147 4t+0.133 4cos0.221 1t+0.012 1sin0.221 1t
(5)

从模型式(3)的决定系数、残差分析来看,当n=1,2时,模型的拟合效果不及n=3的情形;当n>3时,模型的拟合效果未得到显著改善。依据模型结构力求简单、运算量尽可能小、精确度尽可能高的原则,选择n=3的模型为大坝变形最终的预测模型。需要指出的是,利用模型式(5)计算出的拟合预测值还需要按下式进行数据还原:
(6)

该大坝前32期变形监测的原始监测数据与模型拟合曲线,见图4。
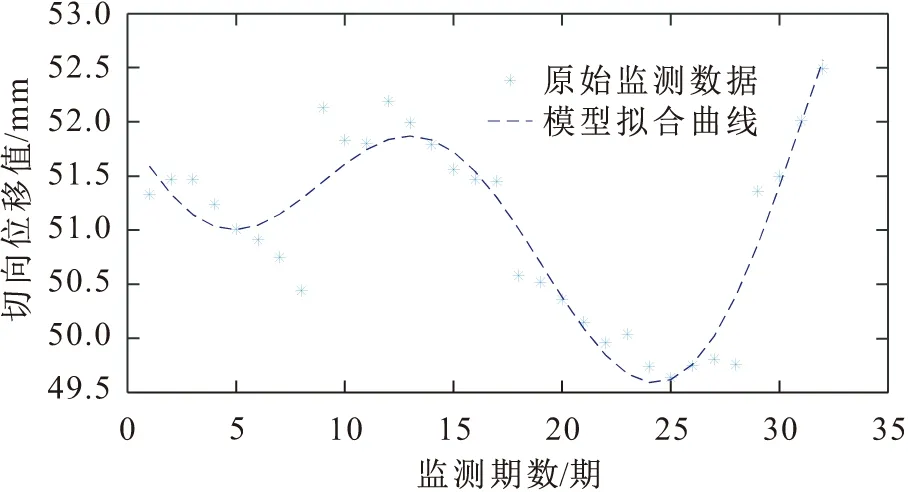
图4 某大坝前32期变形监测的原始数据与模型拟合曲线
作为对比,本文给出了未经光滑处理的该大坝前32期变形监测原始数据的傅立叶级数模型:
y=51.15+0.467 9cos0.178 2t+0.578 4sin0.178 2t+0.487 8cos0.356 4t-0.755 7sin0.356 4t+0.182 7cos0.534 6t-0.231 8sin0.534 6t
(7)

本文利用模型式(5)、(6)以及模型式(7)对该大坝后4次变形进行预测,并将其预测结果与文献[2]的预测结果进行了对比,详见表2和表3。

表3 大坝变形预测模型的精度比较
注:绝对误差=|预测值-实际值|;相对误差=|(预测值-实际值)÷实际值|×%。
由表3可知,本文建立的基于函数cot(x2)变换的傅立叶级数(Fourier)大坝变形预测模型(简称cot(x2)-Fourier模型)的预测精度(最大绝对误差不超过0.087 4,平均相对误差仅为0.099 5%)明显高于另两种预测模型。究其原因分析认为:大坝变形的原始监测数据呈现离散断裂状、波动性大、规律性差等特点,对这类数据列不适合采用参数回归模型(需要事先设定)来表征,而适合采用非参数回归模型(基函数的代数和)来逼近实际变形曲线(尽管未知),而傅立叶级数能任意逼近在区间[-l,l]上的连续函数(或仅有第一类间断点的函数),故本文选用傅立叶级数建模;另外,数据的光滑程度直接关系着傅立叶级数模型的逼近效果,所以在建模前应对建模数据进行平滑处理,本文通过函数cot(x2)变换提高了大坝变形原始监测数据的光滑度,从而提高了预测模型的预测精度,实例应用也证明了这一点。
3 结 论
受监测条件、地形地貌、地质构造、周围环境和气候环境等因素的影响,大坝变形的原始监测数据往往呈现离散断裂状、非光滑性、规律性差等特点,对这类数据列如果采用事先设定的变形曲线模型进行拟合预测,常常会发生因设定不当而出现较大偏差的现象,而傅立叶级数能够逼近任意连续函数(或仅有限个第一类间断点),利用傅立叶级数建模可以有效地避免这种现象的发生。大坝变形或其他建筑物变形均为时间的未知连续函数(可能存在第一类间断点),非常适合利用傅立叶级数逼近该变形函数,但因数据的光滑度对傅立叶级数逼近效果有较大的影响,所以在建模前应对大坝变形的原始监测数据进行平滑处理。函数cot(xα)变换是一种被理论证明能提高数据光滑度的方法,基于函数cot(xα)变换的傅立叶级数模型法具很强的数据表达能力,对建筑物后期变形的预测具有较高的精度,而且利用傅立叶级数建模只需少量级数项就能取得理想的预测效果,这种优点有利于工程实践。
