基于激光三角测量的视觉测量方法研究

李叶萌，詹金辉，席国庆，胡随芯

(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070；2.武汉理工大学 汽车零部件技术湖北省协同创新中心，湖北 武汉 430070；3.湖南江南汽车制造有限公司 湖北分公司，湖北 襄阳 441000;4.湖北三环锻造有限公司，湖北 谷城 441700)

零件的尺寸检测是企业产品质量监督与控制的重要环节。随着企业对生产成本和生产效率的要求不断提高，传统的尺寸检测方法已经无法满足企业的需求。随着数字图像处理技术的出现和发展，视觉测量技术成为工业界零件尺寸检测的重要手段之一。视觉测量相对传统的量检具测量，具有测量效率高、成本低、适应范围广等特点，更适合大尺寸和外形复杂物体的检测[1]，在三维重建和逆向工程等方面的优势更为突出。

采用激光辅助的激光三角测量法可以利用激光的变化来确定被测物的空间位置[2]。激光平面测量模型主要分为相机标定模型和激光平面标定模型两个部分。国内外的研究主要集中在激光平面标定模型的部分。刘凤梅等[3]提出基于齿形靶标的激光平面标定模型，这种标定模型采用的靶标比较特殊，标定过程较为复杂。Wei等[4]提出利用双交叉比不变性来估计光平面参数的模型，俞乾等[5]提出二维靶标多位姿标定法，两者采用普通的二维靶标，但只求解了激光平面的表达式，未给出相机相对激光平面的位置关系，使得其依赖世界坐标系的位置。笔者对激光三角平面测量模型进行改进，进一步推出相机与激光平面的位置关系，以解决世界坐标系难以获得或容易改变的问题。

1 激光三角平面测量模型

激光三角平面测量模型是对点激光三角测量法的拓展。传统点激光三角测量法采用点激光器和线阵CCD(charge coupled device)相机，激光器照射到被测物表面并发生反射，在相机光敏面上成像[6]。点激光三角测量原理如图1所示，当物体高度变化为Δh时，线阵CCD光敏面上也产生相应Δx变化，从而获得被测物体某一点相对于基准平面的高度。

图1 点激光三角测量原理图

点激光三角测量法虽然结构简单，但受到激光器的限制，只能获得单一的尺寸，且测量效率较低。因此，笔者建立了一种激光三角平面测量模型，测量原理与点激光三角测量法相似，采用线激光器和面阵CCD相机，其结构原理如图2所示。激光器投射出一个激光平面，激光平面与被测物体相交产生随被测物体表面形状变化的激光线条，即被测物体的截面轮廓线。使物体沿激光平面法线在被测物体所在平面投影的方向移动，从而获得多条物体轮廓线，通过拼接得到物体表面几何特征。

图2 激光三角平面测量原理图

传统激光三角平面模型只给出了相机坐标系与基准面世界坐标系的转换关系，在实际测量中世界坐标系有时难以获得。一旦世界坐标系位置发生变化，则需重新标定位置关系。激光三角平面测量模型中，激光平面与相机相对位置固定，当建立相机坐标系与激光平面坐标系的位置关系时，在测量范围内被测物体摆放的基准面高度以及放置姿态将不会影响测量结果。图3为相机与激光平面的标定模型。图3中(u，v)为像素坐标系，(x，y)为图像坐标，(Xc，Yc，Zc)为相机坐标系，(Xw1，Yw1，Zw1)为平面P1坐标系，(Xw2，Yw2，Zw2)为平面P2坐标系，(Xl，Yl，Zl)为激光平面坐标系。P1、P2平面平行且高度差为h，为了保证测量精度，通常该高度差应大于被测物的高度。

图3 相机与激光平面的标定模型

根据相机针孔成像原理建立的相机的成像模型，像素坐标系(u，v)与平面P1坐标系(Xw1，Yw1，Zw1)以及平面P2坐标系(Xw2，Yw2，Zw2)的转换关系[7]为：

(1)

(2)

式中：dx、dy分别为x、y方向上单个像素的长度；u0、v0为图像坐标的原点；s为比例系数；f为相机焦距；R1为3×3旋转矩阵；T1为3×1平移向量；M为相机的内部参数；M1、M2为标定板在平面P1、P2时的相机外部参数。

由式(1)和式(2)可以得到平面P2坐标系与平面P1坐标系的转换关系为：

(3)

激光平面在平面P1和P2内分别投影有一条激光线，利用相机记录两条激光线的图像。通过式(1)和式(2)坐标转换关系对激光线图像进行处理，得到其在相应平面坐标系下可表示为：

[A1B10D1][Xw1Yw1Zw11]T=0

(4)

[A2B20D2][Xw2Yw2Zw21]T=0

(5)

将式(3)代入式(5)得:

[A1B1hD′2][Xw1Yw1Zw11]T=0

(6)

式中：A1、B1、D1、A2、B2、D2和D′2为空间直线常系数。

两条激光线相互平行且式(4)和式(6)统一在平面P1的坐标系下，激光平面在平面P1坐标系下的方程可以表示为：

AXw1+BYw1+CZw1+D=0

(7)

式中：A、B、C和D为空间平面系数。

通过式(1)和式(7)即可获得物体在平面P1坐标系下的三维坐标。取激光平面内一点(xl，yl，zl)为原点建立激光平面坐标系，设Ml-1为平面P1坐标系与激光平面坐标系转换矩阵，由式(1)和式(7)可推得平面P1坐标系与激光平面坐标系关系为：

(8)

设Ml为相机相对于激光平面的外部参数矩阵，最终得到激光平面坐标系与图像坐标系的转换关系为：

(9)

上述数学模型忽略了相机镜头带来的图像畸变的影响，实际应用中会引入畸变系数对图像进行畸变矫正。相机非线性畸变可以分为径向畸变、切向畸变和薄棱镜畸变，其中径向畸变对图像的影响最大[8]。为了更准确补偿图像畸变，选取了3个径向畸变系数(k1、k2、k3)和2个切向畸变系数(p1、p2)。

2 测量系统标定

标定是对已建立相机模型中未知参数的求解过程，利用已知特征点建立图像坐标系和世界坐标系位置关系。相机的标定参数包括内部参数和外部参数两个部分。内部参数是相机固有参数，包括焦距、像素长度、图像尺寸和图像原点和畸变系数等，这些参数不随相机的位置变化。外部参数则是确定相机坐标系与世界坐标系位置关系，可以用旋转矩阵和平移向量来表示。根据建立的模型搭建实验平台，相机型号为piA2400-17gm-Basler pilot，线激光器为HA345050L-AL，波长450 nm，相机光轴与线激光器投射平面呈25°。采用张正友标定法，用相机拍摄多个方位的平面靶标，求解相机的参数。采用2D平面靶标对相机进行标定，标定板如图4所示。标定板由7×7个实心圆阵列组成，圆的直径为10 mm，相邻两个圆的圆心距为20 mm，外框黑线的尺寸为160×160 mm，标定板尺寸精度为0.1 mm。

图4 2D标定板

利用Halcon软件的图像采集助手，在相机的视野范围内移动标定板并拍摄一定数量标定板图像，导入标定程序对相机的内部参数进行标定，图5为标定板在不同位置采集的图形。通过6次标定对结果取平均值，获得相机的内部参数如表1所示。

图5 标定板采集图像

内部参数标定值内部参数标定值焦距f/mm11.14k1/px/m21.57×103单个像素长度dx/μm6.25k2/px/m4-7.44×106单个像素长度dy/μm6.25k3/px/m6-1.39×1011图像原点u0/px1 274.61p1/px/m20.046 9图像原点v0/px1 014.65p2/px/m4-0.007 1标定误差/μm0.243

相机的外部参数需要分两步来标定，首先拍摄标定板在P1平面上的图像和此时的激光线条图(图6)，之后保持标定板位姿不动，将工作台面提高一定距离，拍摄标定板在P2平面上的图像和此时激光线条图(图7)。通过自定义算子compute_light_pose，计算P1、P2平面内相机外部参数，并对激光平面进行拟合。

图6 P1平面标定板及激光线条图像

图7 P2平面标定板及激光线条图像

实际光平面拟合是通过3点确定平面来完成的。在P1平面激光线条上选取两个点，P2平面激光线选取一个点，通过3点确定激光平面的法向量，以3点确定圆心为激光平面坐标系的原点，从而建立激光平面坐标系。为了更准确地标定，通过多次选点来进行拟合，以激光线条上点的平均距离残差来评价拟合效果，当平均残差值小于7×10-5时，认为激光平面的拟合符合测量要求。最终标定得相机相对平面P1外部参数M1和相机相对激光平面法外部参数Ml为：

3 几何测量及误差分析

选取尺寸已知的样块，测试测量系统在P1平面坐标系下xyz3个方向上的误差分布。将样块依次放置在移动平台上，以5 mm/s的速度沿x方向匀速移动，相机以17帧/s的速度对被测物上的激光线条进行拍摄。激光线条投射在被测物体表面，由于物体表面的反射作用，加上环境光照的影响，图像会产生噪声。在对图像进行滤波处理后，图像分为高亮度激光线条和黑色背景两个部分。设定一定灰度阈值，提取出主要的激光线条部分。拟合激光线条的外包围轮廓线，计算轮廓线在每个像素列方向中点作为激光线条的中心线[9]。将中心线离散成点，并转换到世界坐标系下，获得单张图像激光线条的点云数据[10]。将激光线条沿x方向等距拼接在一起，最终获得样块的部分表面三维点云数据。利用Geomagic Studio对点云进行修补、平面拟合以及尺寸测量，获得各方向误差变化如图8～图10所示。

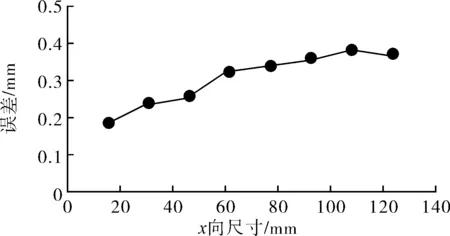
图8 x方向误差

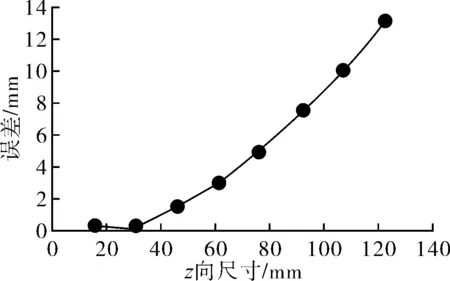
图9 z方向误差

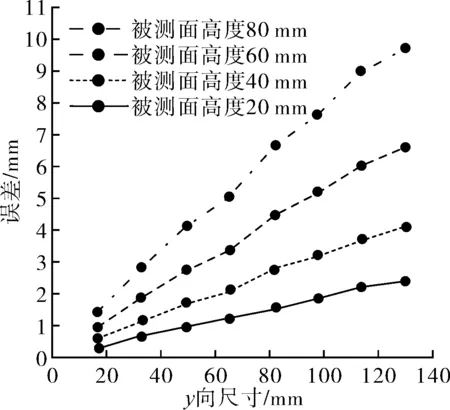
图10 y方向误差变化

激光线条拼接时的距离是平台移动速度与相机帧率的比值，由于此为理论计算得出的，因此在样块移动方向上(x方向)测量误差随尺寸变换很小。而在样块的yz两个方向上，系统的测量误差都与测量的尺寸相关。在z方向上，随着样块z向尺寸的增加，测量误差加速上升，误差增长近似为2次曲线。而在y方向上，误差与样块尺寸基本呈线性增长关系，与此同时，随着样块被测面所处高度的增加，误差值也随之提高了。

从图8～图10中可知，测量系统在一定测量范围内，测量误差较小。设定测量系统的工作精度为0.5 mm，则通过相机与工作平面的相关参数，可以得到该测量系统的工作高度范围为380～440 mm。

4 结论

(1)针对传统激光三角平面测量法在实际应用中世界坐标系难以确定的问题，建立了以激光平面为测量面的数学模型，推导了相机与激光平面坐标的转换关系，提高了测量系统的灵活性。

(2)通过实验得到系统的测量误差，获得了其在不同方向上的分布规律，最终确定测量系统的精度以及工作范围。