基于综合指标的机床滚珠丝杠进给系统动态性能优化

2019-10-10朱其新

农业机械学报 2019年9期

杨勇孙群朱其新陈盛

(1.苏州科技大学机械工程学院, 苏州 215009； 2.苏州科技大学苏州市精密与高效加工技术重点实验室, 苏州 215009；3.上海电机学院机械工程学院, 上海 201306； 4.南京邮电大学自动化学院，南京 210023)

0 引言

机床滚珠丝杠进给驱动系统[1]作为一个典型的机电耦合系统，其伺服控制输出的力直接作用于机械传动环节，而机械传动环节的位移、速度、加速度一方面会影响机械系统的运动特性，另一方面其作为反馈信息反馈至伺服控制会影响伺服控制及整个滚珠丝杠进给驱动系统的运动响应性能[2-3]，受进给驱动系统机械结构振动的影响，需降低位置环增益以确保整个进给系统的稳定性。为分析整体滚珠丝杠进给驱动系统的运动响应特性[4-5]，需要对该系统集成建模，以往研究学者在集成建模时多采用在不同仿真环境下分别对机械和控制子系统建模，通过软件接口的信息交互实现机械传动与伺服控制耦合集成模型，但受限于软件接口的兼容性、扩展性，集成模型精度和效率会受到影响[6-7]。

在对滚珠丝杠进给驱动系统运动响应特性进行评价时，可以选用超调量、调节时间、上升时间、稳态误差等响应特征[8-10]，但这些响应特征仅能表征某项品质指标，且因其数量级差异较大难以采用多目标优化方法实现运行响应性能的综合评价[7]。

为此，众多研究中引入系统理想输出和实际输出之间的误差函数评价系统的运动响应性能，如平方误差积分函数ISE、时间乘平方误差积分函数ITSE等。相较于前述响应特性评价指标，该误差函数在一定程度上实现了对系统综合响应性能的表征，但不同的误差积分准则函数同样侧重于不同的运动响应性能表征，如时间乘绝对误差积分准则函数ITAE虽然能确保系统瞬态响应振荡较小，但很难保证幅值稳定裕度；而平方误差积分准备函数ISE具有较快的响应速度但是振荡性较大，稳定性较差。可以看出，这些误差函数仍相对侧重于运动响应的某些特征指标，仍然无法根据优化需求综合评价系统运动响应性能，且当选取某一误差积分函数作为优化目标函数时，无法根据优化需求对系统性能及伺服参数进行实时调节。

本文建立滚珠丝杠进给系统理论动力学模型并对其响应传函特性进行分析，并构建基于数字化模块仿真的滚珠丝杠进给驱动系统集成模型，通过状态空间表示法在同一仿真环境下建立并集成机械结构与伺服控制子模块模型。提出基于扩缩式伺服控制优化模型的滚珠丝杠进给驱动动态性能优化方法，建立滚珠丝杠进给系统可扩缩式伺服控制优化模型，构建面向综合指标评价的可扩缩式动态性能指标评价函数，根据动态性能优化要求实时建立动态性能综合评价指标函数，通过运动路径规划定义，借助遗传优化算法，实现面向可扩缩式综合指标评价的滚珠丝杠进给驱动系统动态性能优化。

1 滚珠丝杠进给系统理论动力学建模与分析

滚珠丝杠进给系统示意图见图1a，其包含电机、联轴器、丝杠、螺母、导轨、工作台等，联轴器将电机的往复旋转运动传递至丝杠，丝杠螺母副将丝杠的往复旋转运动转换为螺母的往复直线运动，螺母与工作台之间的固定联接使螺母带动工作台沿着导轨往复运行。

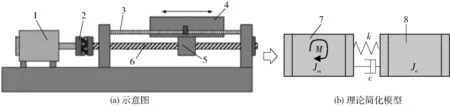
图1 滚珠丝杠进给系统理论动力学简化模型Fig.1 Simplified modeling of theoretical dynamics for ball screw feeding system1、7.电机 2.联轴器 3.导轨 4.工作台 5.螺母 6.丝杠 8.等效负载

滚珠丝杠进给系统动力学理论简化模型如图1b所示，其将电机作为动力件，其转动惯量为Jm，由电机带动的联轴器、丝杠、螺母、工作台作为负载，设其等效负载转动惯量为Je，电机输出力矩为M，电机和等效负载之间存在等效刚度k和等效阻尼系数c。以联轴器作为等效构件，选取联轴器角速度ωc为等效构件角速度ωe，根据等效前后能量守恒定理可得

(1)

式中Jc、Js——联轴器和丝杠的转动惯量

mn、mt——螺母和工作台质量

ωs——丝杠角速度

vn、vt——螺母和工作台的移动速度

根据式(1)可得

(2)

根据各运动变量之间的关系，拉氏变换为

(3)

式中φm、φe——电机与等效负载的角位移

ωm——电机角速度

αm、αe——电机与等效负载的角加速度

对电机与等效负载分别进行受力分析，可建立其动力学基本方程并进行拉氏变换得到

(4)

将式(3)代入式(4)可得

(5)

基于自动控制原理，可分别得到式(3)、(4)的信号流图，并最终综合为整体信号流图如图2所示，可以看出其物理变量之间存在相互耦合关系。基于梅森增益公式，求解M(s)与φm(s)之间的传递函数为

(6)

其中Δ=1-∑La+∑LbLc-∑LdLeLf+…

式中 ∑La——所有单独回路增益之和

∑LbLc——两两不接触回路增益乘积之和

∑LdLeLf——每3个互不接触回路增益乘积之和

pk——第k条前向通路总增益

Δk——流图余因子式，其等于去掉与第k条前向通路接触的回路后的流图特征式

分析可得

(7)

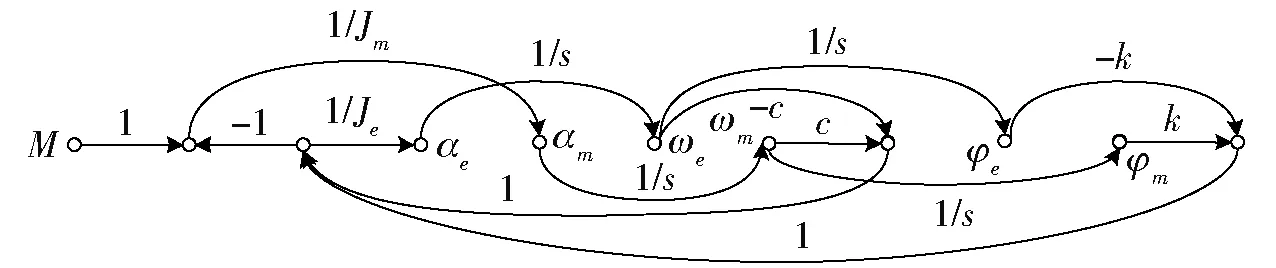
图2 滚珠丝杠进给系统理论动力学模型信号传递流程图Fig.2 Signal transfer flow chart of theoretical dynamic model of ball screw feed system

将式(7)代入式(6)最终化简可得

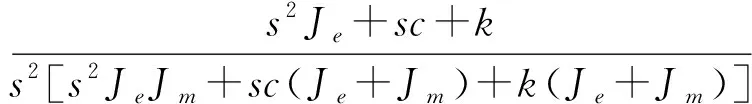
(8)

从式(8)可以看出，其分子是典型二阶系统传递函数的标准形式，依据二阶系统无阻尼自然频率ωn以及阻尼比ζ公式可知

(9)

(10)

将式(8)分子分母同除以Je，并将式(9)、(10)代入式(8)可得

(11)

在上述基础上进一步求解φm(s)和φe(s)之间的传递函数P2。令M等于0并且去掉其关联部分，将φm(s)作为输入，对图2进行简化可得φm(s)和φe(s)之间的传递函数框图如图3所示，同样采用梅森增益公式求解其传递函数可得

(12)

将式(9)、(10)代入式(12)，最终可得

(13)

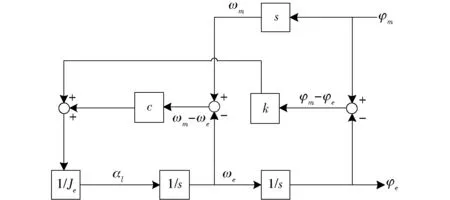
图3 电机转角到等效负载转角的传递函数框图Fig.3 Transfer function diagram of motor rotation angle to equivalent load rotation angle

由式(12)可以看出，其分母为典型的二阶传递环节，而其分子为典型的一阶延迟传递环节，其综合作用的结果是幅值响应曲线在系统固有振动频率处下降。因此可知，其系统固有频率对伺服控制回路中的实际位置及位置环增益参数产生重要的影响，只有在低于该振动频率的控制带宽内，控制信号才能无衰减无延迟传递。

此外，可以看出，力矩与电机输出转角之间的传递函数P1、电机转角与负载转角之间的传递函数P2的零极点发生颠倒，传递函数P2的极点即为传递函数P1的零点，因此根据其零极点对应关系，在通过频响函数P1测试确定系统固有频率时，亦可以通过频响函数P2的零极点测试确定系统固有频率。

2 基于数字化模块仿真的滚珠丝杠进给驱动系统集成建模

根据数字化模块仿真方法，将滚珠丝杠进给驱动系统分为伺服控制子模块和机械传动子模块，进一步通过状态空间表示法[11-12]在同一仿真环境下建立并集成机械结构与伺服控制子模块模型，整体流程示意图见图4。

图4 基于数字化模块仿真的整体滚珠丝杠进给驱动系统建模示意图Fig.4 Modeling schematic of whole ball screw feed drive system based on digital module simulation

状态空间表示法是通过含状态变量的微分方程组建立系统内部状态变量与外部输入变量和输出变量间的关系。通过系统的动力学微分方程或系统的传递函数/传递函数框图均可建立基于状态空间表示法的系统模型。通常采用传递函数/传递函数框图对伺服控制系统进行建模，而常采用动力学微分方程对机械系统进行结构动力学建模。故状态空间表示法可很方便实现同一仿真环境下的机械传动与伺服控制的数字化模块建模集成。

实际机床滚珠丝杠伺服驱动系统常采用经典级联式控制，作者在文献[13]中已建立了基于传递函数框图的滚珠丝杠进给系统级联伺服控制模型，见图4中基于传递函数框图的伺服驱动模型。经计算，滚珠丝杠进给驱动位置环传递函数G(s)可以简化为

(14)

式中φi(s)——滚珠丝杠进给系统伺服控制的理想输入位置

φo(s)——滚珠丝杠进给系统伺服控制的实际输出位置

b0、b1、…、bn——滚珠丝杠伺服控制传递函数的分子系数

a0、a1、…、an——滚珠丝杠伺服控制传递函数的分母系数

采用长除法，将式(14)转换为

(15)

其中

设E为单位矩阵，将上述各式写作矩阵形式为

(16)

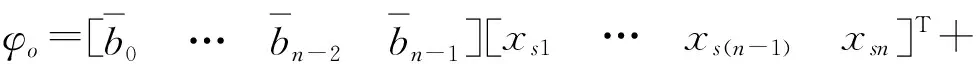
(17)

令

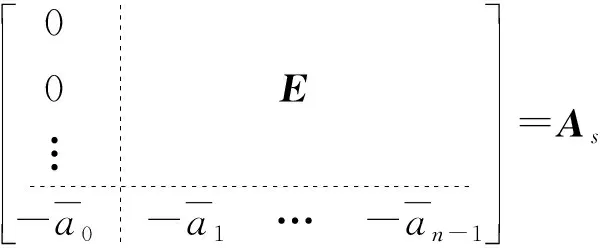
代入式(16)、(17)可得滚珠丝杠伺服控制状态空间表达式为

(18)

滚珠丝杠机械传动环节的输入输出量分别为电机扭矩与机械结构位移矢量，基于有限元的滚珠丝杠机械结构模型(图4)的结构动力学方程为

(19)

式中Mj、Cj、Kj——滚珠丝杠机械结构的质量、阻尼、刚度矩阵

xj——滚珠丝杠机械结构位移矢量

Q——电机输出扭矩，其为滚珠丝杠机械传动环节的输入力

根据状态空间表示法，可得滚珠丝杠机械传动环节状态空间表达[13]为

(20)

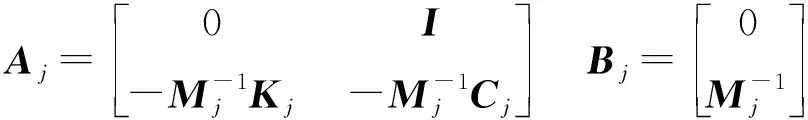
需要注意的是：在构建上述滚珠丝杠伺服控制状态空间表达时，将滚珠丝杠机械传动环节简化为等效转动惯量J的刚体来表达输入Q与输出xj之间的关系，而实际基于该滚珠丝杠机械传动环节状态空间表达的输入Q与输出xj间关系，同样可得到如式(16)、(17)的基于状态空间表示法的滚珠丝杠进给驱动整体标准式。

滚珠丝杠机械传动环节结构部件的建模方法及具体参数见图4，此外在实际建模过程中滚珠丝杠伺服控制系统的相关参数为位置环增益Kv=25 s-1，速度环增益Kp=27.3 N·m·s/rad，速度环积分时间Tn=60 ms，电流环增益Ki=12.157 V/A，电流环积分时间Ti=2 ms，电感系数La=3.1 mH，电阻系数Ra=0.075 Ω，反电势系数Ke=1.67 V·s/rad，扭矩系数KT=2.72 N·m/A。

3 基于扩缩式伺服控制优化模型的滚珠丝杠进给驱动动态性能优化

提出基于扩缩式伺服控制优化模型的滚珠丝杠进给驱动动态性能优化方法，建立滚珠丝杠进给系统可扩缩式伺服控制优化模型，构建面向综合指标评价的可扩缩式动态性能指标评价函数，根据动态性能优化要求实时建立动态性能综合评价指标函数，通过运动路径规划定义，借助遗传优化算法，实现面向可扩缩式综合指标评价的滚珠丝杠进给驱动系统动态性能优化。

3.1 扩缩式伺服控制优化模型构建

3.1.1路径运动规划数学建模

为保证数控机床伺服运动的可靠性，避免起停运动的冲击、失步、超程等，在同样的起点终点位置(直线)间，数控系统可以采用不同加减速控制算法实现不同的路径运动规划，传统数控系统中常用的加减速算法有直线型加减速和指数型加减速。这两种方式在启动和结束时均存在加速度突变，容易产生冲击，因此不适用于高速高精度数控系统。通常高速高精度数控系统加减速路径规划可以分为两类：插补前加减速控制和插补后加减速控制。实际加工过程中常采用指数型控制算法作为插补前控制，而采用钟型加减速控制算法(加减速算法在加减速阶段不存在加速度突变的现象)或者多次项加减速算法(加加速度无突变现象)作为插补后控制[14-15]。

为了降低其伺服跟随延迟应尽量使各轴位置环增益相同，在保持系统稳定的前提下位置环增益尽量取大值，同时可以选择较好的加减速控制方式降低加减速延迟轨迹误差。根据现代机床的高速高精度特点，并且考虑到实际加工，选取插补后多项式加减速控制算法作为扩缩式伺服控制优化模型的路径运动规划以降低加减速延迟轨迹误差，此时伺服跟随误差对加工误差的影响性更为突出，其可通过选择合适的控制参数来降低误差。

通过函数叠加法，建立该伺服控制优化模型的多项式加减速控制算法的加加速度的数学式

(21)

(22)

式中jmax——最大加加速度设定值

hi——heaviside分段函数

将式(21)中的加加速度路径规划定义式进行拉氏变换，可得

(23)

式中L——拉氏变换计算

加加速度j、加速度a、速度v、位移q之间的关系为

(24)

式中L-1——拉氏逆变换计算

对式(24)进行拉氏变换与拉氏逆变换，最终可得该伺服控制优化模型的路径运动规划加加速度、加速度、速度、位移曲线如图5所示。

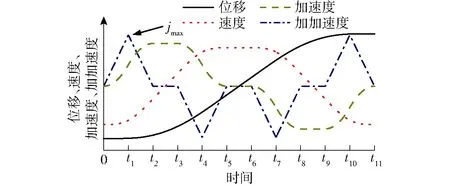
图5 滚珠丝杠进给系统伺服控制优化模型的路径规划曲线Fig.5 Path planning curves of servo control optimization model for ball screw feed system

在实际路径规划定义时，文献[16]采用C++语言S函数方法实现路径规划定义，而本文采用Matlab中的sim函数定义滚珠丝杠进给系统伺服控制优化模型路径规划。

3.1.2优化变量选取

通常伺服控制系统采用级联控制对位置环、速度环以及电流环的增益及积分时间进行优化，但是由于电流环控制参数可以通过电机生产商取得，并且不需要通过复杂的伺服仿真模型便可以进行调整，因此，本文选取速度环增益、积分时间、位置环增益3个参数进作为优化变量。

3.1.3评价函数

根据动态性能优化要求实时建立滚珠丝杠进给系统动态性能综合评价指标函数，将上述动态响应误差函数等定义为系统性能指标(System performance index, SPI)，基于二次型评价指标原理，构建滚珠丝杠进给系统响应特性的的扩缩式目标评价函数(Scalable objective evaluation function, SOEF)数学表达式为

(25)

式中n——系统性能评价指标数量

wi——单个性能指标在整体评价函数中所占的权重

从式(25)可以看出，如果权重系数wi置为0，则对应的性能指标不会对整体评价函数产生任何影响，而如果该权重系数增加，则其对整体评价函数的贡献增大，反之亦然。因此，可以通过该权重函数的选择实现滚珠丝杠进给系统动态性能评价指标的可扩缩性及系统动态性能评价指标配重调整。

从式(25)可以看出，指标评价函数具有确定的函数形式，具有可扩缩性。根据动态性能优化需求，可方便地对动态性能指标评价函数进行调整，动态性能优化需求不同时，无需重新构造指标评价函数，无需重新设置动态性能不同评价指标之间权重函数，指标评价函数构造可更加快速与便于调整。

滚珠丝杠进给系统性能指标SPI可以选用对响应特征值综合处理的理想输出和实际输出之间的标准误差积分函数如ISE、ITSE等，亦可以根据需求自定义滚珠丝杠进给系统性能指标SPI，如本文后续优化时则采用式(26)所示的自定义SPI函数反映滚珠丝杠进给系统动态响应的超调与暂态震荡。

(26)

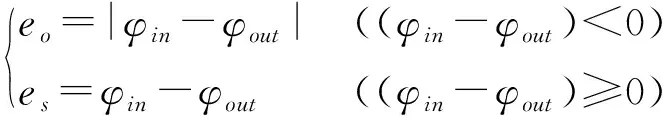
式中fo、fs——以时间为变量的超调与暂态震荡的加权系数

3.1.4优化算法确定

在前述路径运动规划数学建模、面向综合指标评价的可扩缩式动态性能指标评价函数构建、优化变量选取等的基础上，进一步选择滚珠丝杠进给驱动动态性能优化过程中的智能优化算法。基于遗传优化算法的自适应全局优化搜索特点，选取遗传优化算法进行面向综合指标评价的滚珠丝杠进给驱动动态性能优化。

3.2 结果与分析

采用西门子840D型数控系统[17-18]机床，通过西门子840D系统内置的面板控制单元PCU50，以及相应的集成于操作界面软件HMI Advanced上的测试工具Start-up tool(IBN-Tool)[17-20]，可以实现机床滚珠丝杠进给驱动系统动态性能频率响应测试，其频响测试信号来源于机床滚珠丝杠进给驱动系统内置的电机编码器、霍尔电流传感器等内置传感器。

基于该机床滚珠丝杠进给驱动系统内置传感器型号，借助面板控制单元PCU50和频响测试工具Start-up tool(IBN-Tool)，得到的滚珠丝杠进给驱动系统电机转角与负载转角间频响P1、电机转角与负载转角之间的传递函数P2如图6所示。滚珠丝杠进给系统仿真计算频率、P1频响(零极点)、P2频响(零极点)的对应关系见表1。

图6 P1(电机转角与负载转角间频响)与P2(电机转速与力矩间频响)的零极点对应关系Fig.6 Aero-pole correspondence relationship between P1 (frequency response between motor rotation angle and load rotation angle) and P2(frequency response between motor speed and torque)

综合图6与表1可以看出，力矩与电机输出转角之间频响函数P2、电机转角与负载转角之间频响函数P1的零极点发生颠倒，这与前述滚珠丝杠进给系统理论动力学建模分析结论相符；力矩与电机输出转角之间频响P2的零点(29.61、78.13、117.20 Hz)即为电机转角与负载转角之间频响P1的极点(29.05、70.07、116.10 Hz)；电机转角与负载转角之间频响P1的零点即为力矩与电机输出转角之间频响P2的极点，且P2极点(45.44、85.94、130.90 Hz)、P1零点(45.20、86.40、149.20 Hz)与滚珠丝杠进给驱动系统仿真计算频率(47.96、90.74、142.16 Hz)误差较小。由图6可知，在第1个极点位置即一阶固有频率处，幅值响应计算值(35.16 dB)与测试值(32.83 dB)相差较小，从图6也可以看出，滚珠丝杠进给系统仿真计算曲线与实测曲线吻合度较好。综上分析，说明所构建的滚珠丝杠进给系统理论动力学建模与分析结论的正确性，验证了基于数字化模块仿真的滚珠丝杠进给驱动系统集成模型的正确性。

在此基础上，根据前述基于扩缩式伺服控制优化模型的滚珠丝杠进给驱动动态性能优化方法，借助前述滚珠丝杠进给系统可扩缩式伺服控制优化模型，采用不同的优化情形实例，根据动态性能优化要求实时建立动态性能可扩缩式综合评价指标函数，实现面向可扩缩式综合指标评价的滚珠丝杠进给驱动系统动态性能优化。

优化情形1：当选取滚珠丝杠进给系统理想输出和实际输出间平方误差积分为滚珠丝杠进给系统性能指标SPI1时，即SPI1=ISE，根据可扩缩式目标评价函数得到的滚珠丝杠进给系统动态响应SOEF数学式为SOEF=SPI1。此时更强调滚珠丝杠进给系统的快速响应特性而对系统振荡关注较少，优化后得到的动态响应曲线见图7中优化曲线1，可以看出相比于优化前阶跃响应曲线(上升时间与调节时间均为0.152 s)，该曲线响应速度较快(上升时间0.034 s)，调节时间相对较短(0.084 s)，但有略微超调且动态响应的稳定性较差。这些与ISE误差积分函数动态响应评价特性优化需求相吻合。

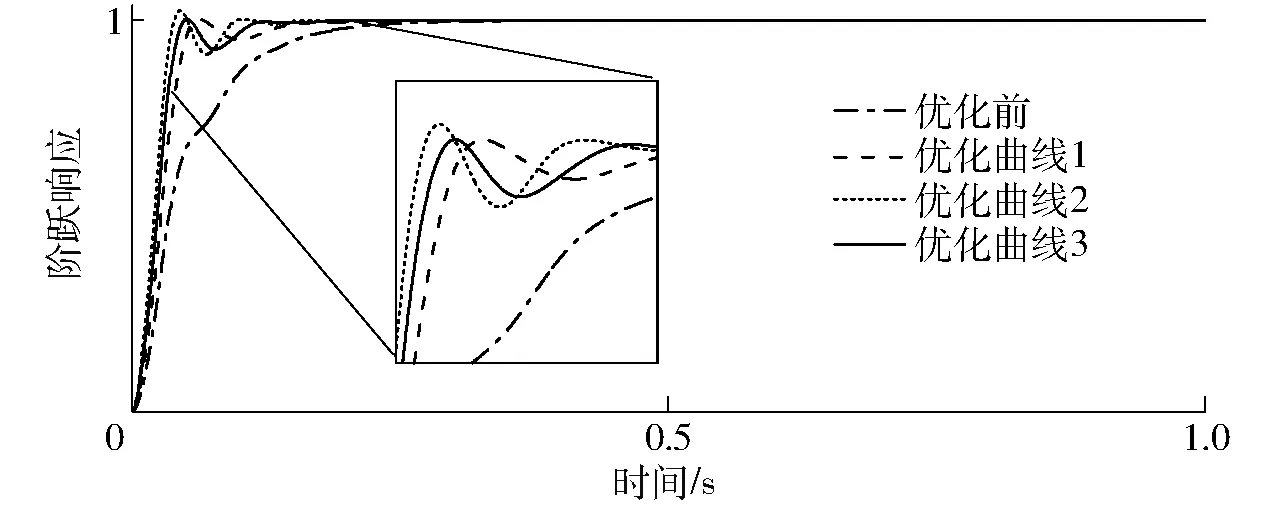
图7 不同优化情形下的滚珠丝杠进给驱动系统动态响应优化结果Fig.7 Dynamic response optimization results of ball screw feed drive system under different optimization conditions

优化情形2：在前述基础上，基于面向综合指标评价的可扩缩式动态性能指标评价函数，若更加注重滚珠丝杠进给系统的稳定性需求，即系统在高速运行时动态响应稳定，进一步选取滚珠丝杠进给系统理想输出和实际输出间时间乘绝对误差积分ITAE为滚珠丝杠进给系统性能指标SPI2，且指定SPI2具有相对较大的权重系数，即w1=1，w2=2，且f1=1，f2=2，根据可扩缩式目标评价函数最终得到的滚珠丝杠进给系统动态响应SOEF数学式为SOEF=(f1(SPI1)f2(SPI2)2)1/3。优化后得到的动态响应曲线见图7中优化曲线2，分析可得，相比于前一动态响应评价特性优化需求，该动态响应稳定性很好，虽响应速度(上升时间0.050 s)略微降低，但无超调现象出现，且调节时间(与上升时间相同均为0.050 s)很短，与其预设的动态性能优化需求一致。

综上可以看出，通过该基于扩缩式伺服控制优化模型的滚珠丝杠进给驱动动态性能优化方法，根据动态性能优化要求采用不同的优化情形实例建立动态性能可扩缩式综合评价指标函数，得到的面向综合指标评价的滚珠丝杠进给驱动系统动态性能优化结果，与预设的动态性能优化需求一致，也说明该基于扩缩式伺服控制优化模型的滚珠丝杠进给驱动动态性能优化方法的正确性。