双层柱状结构对声表面波芯片的声场调控仿真*

唐帅， 梁辰， 许丽萍, 温廷敦 ， 韩建宁

(1.中北大学 理学院，山西 太原 030051;2.中北大学 信息与通信工程学院，山西 太原 030051)

微流控芯片是一门研究微液体操纵的系统科学[1].随着科学快速发展，在材料及信息领域的分析方法也变得日新月异，传统的微流操控已经无法满足这些要求.作为其中一项重要的微流控应用技术，声学手段受到了越来越多的关注，与其他技术比较而言，基于声波的微流控操纵具有非入侵而且易于实现等优点[2-3].

最近，基于表面声波(surface acoustic wave)的微流控芯片因为设计灵活，易于大规模批量生产，并且工作频率和强度皆适宜于操控细胞，已经被证明适合于各种生物医学方面的应用[4-6].此外，在生物化学方面，诸如聚合酶链反应、细胞种植以及整形外科等，都需要该种SAW驱动液滴的平移原理来实现，因为该技术可以确保细胞的完整性.然而，目前使用较多的SAW芯片基底都相对单一，严重降低了SAW微流控的效率[9-10].此外，现有大多数研究没有有效地利用传输层的物理场，还是单一的声波传输介质，无法有效改变传输层的声场分布.

本文提出的一种基于双层柱状结构的SAW微流控芯片，将声学超材料与SAW芯片有机结合在一起，实现一系列对声场的有效调控，做到对微粒操控的“按需定制”，使其能够完美地应用于微流控操作.

1 模型设计

传统的声表面波芯片模型如图1(a)所示，由压电晶体基片、吸声材料和一对平行的叉指换能器(IDT)组成.在具体应用中，由于驻波的产生与作用，两个对称IDT之间的表面波传播区域是细胞操纵技术的研究关键.如图1(b)所示，在表面波微流控装置中，叉指换能器通过将输入电信号转变为声波信号在基底进行传播，从而为操纵液滴提供声能，而微液滴正是放置于这两个对称IDT之间，通过声波对微液滴内部的颗粒进行作用，从而达到对颗粒的分选和富集.本文所提出的双层柱状声学微结构正是加工在两个对称IDT之间.

(a)传统的声表面波器件模型示意图 (b)声表面波微流控装置

如图2所示，在对称IDT之间的矩形区域放置一双层柱状声学微结构，该双层微结构内层为铜，外层为橡胶，SAW芯片的基底材料为铌酸锂.其中最内侧圆柱半径为376.5 μm，中间圆柱半径为434.4 μm，最外侧圆柱半径为463.4 μm.

在这项模拟实验中，使用COMSOL Multiphysics软件有限元法进行数值模拟，通过改变频率，得到了不同频率下的声场局域效应.图中所展示材料的参数如下：黄铜的密度 ρb= 8 400 g/m3，声速Cb= 4 400 m/s；橡胶的密度ρr=1 100 g/m3,声速Cr= 900 m/s；铌酸锂的密度ρw= 4 650 g/m3，声速Cw= 3 681 m/s.

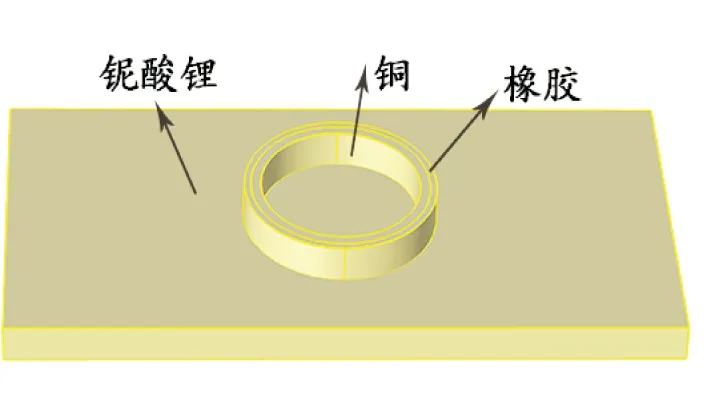
图2 双层柱状声学微结构模型

2 模型的结果和讨论

两侧激励源发出频率为11.453 MHz的入射声波时，如图3 (a)所示，入射波源在铌酸锂基底上进行传播，其表面声场并未发生聚焦现象.图3(b)为存在声学微结构时，同样入射频率为11.453 MHz的声波，在双层柱状结构的本征振动下，入射声源的波形在模型内部重建为一系列同心圆，并最终形成一个圆形焦点，即产生单焦点中心聚焦现象.从图3(c)和3(d)可以看出，仅在声学微结构内部产生很强的单焦点聚焦现象，而在该结构外围的芯片表面上则无较强的声场分布，即声波能量大部分都被声学微结构所吸收.

(a)声源在自由平面传播声场效果图; (b)声波通过声学微结构后声场传播效果图；(c)Y-Z视图；(d)X-Y视图

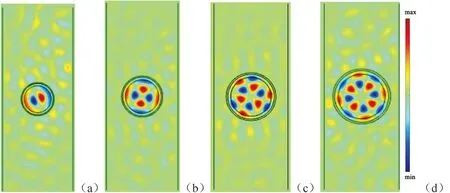
随着入射声波频率的增加，在特定频率下，又会出现类似的中心聚焦现象.当频率为16.050 MHz时，声波仍会集中在模型的中心(图4(a))，但与图3(b)不同的是，由于频率的增加导致波长的减小，因此这个聚焦现象的中心焦点尺寸也相应减小，且聚焦中心外围出现环形波带，随着频率继续增大为20.953 MHz时，聚焦中心外围波带数继续增加，中心焦点尺寸继续减小(图4(b)).

(a)16.050 MHz (b) 20.953 MHz

由于频率的持续增加会导致波长的减小，当波长与所操控微粒尺寸相当时，基于粒子间的异质性，以及双层柱状声学微结构的单点聚焦效果，便能够对微粒进行有效的操控，通过声波辐射力将其从微流体中分离出来.

除了产生中心聚焦现象，该模型在特定频率下也能产生多极点的局域声场.入射不同频率的声波会出现偶极子、四极子、六极子和八极子的情况.在9.091 MHz的激励声波下，如图5(a)所示,会出现2个正负声压交替分布的局域聚焦点，升高频率至11.07 MHz时，如图5(b)所见，会出现4个正负声压交替分布的局域聚焦点，且其中心对称分布，继续升高频率至13 MHz和14.87 MHz时，见图5 (c)和5(d),又会产生六极子和八极子的声场局域现象.

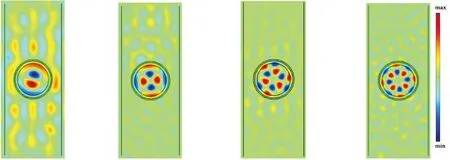
(a)9.091 MHz偶极 (b)11.07 MHz四极 (c)13 MHz 六极 (d)14.87 MHz 八极

随着声波频率的不断变化，以单点聚焦和六极子声场局域现象为例进行分析，当声学微结构存在时，如图6(a)和6(b)的相位变化示意图，在柱状模型的共振作用下，声波的传输路径产生了改变，在圆心处产生汇聚点.由于不同的入射频率会产生不同的波长和相位，当相位受到环状模型的调控时，便会在特定频率下产生一系列多极子的声场局域现象.

(a)单点聚焦现象的声压相位分布 (b)六极子声场局域现象的声压相位分布

当入射声波的频率变化时,发现无论单点聚焦效果还是多极声场局域现象都会随着频率的变大而增加外围的环状波带数，可见这种声场局域现象具有类周期性(如图7).

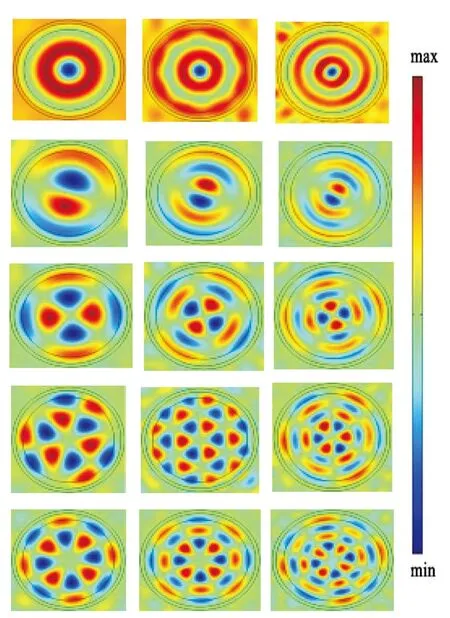
图7 类周期性声场局域效果

声表面波器件往往具有一个最佳工作频率(中心频率)，而声场局域现象的产生对频率又具有一定的依赖性，即在某些特定频率下，可以有效产生声场局域现象，而在另一些特定频率下，又无法有效产生声场局域现象，因此，本文将探究声学模型参数对于产生声场局域现象所需频率的影响，确保在器件的中心频率可以有效实现所需要的声场局域现象.

以13 MHz的表面波器件中心频率为例，当固定入射声波频率为13 MHz时，通过改变空心柱状结构的尺寸，即可使得在该频率下分别实现偶极、四极、六极以及八极等声场局域现象(如图8(a)-(d)).

为了探究声学模型尺寸与实现声场局域现象所需频率间的对应关系，本文将空心圆柱的半径等比例变化，在每个不同尺寸的模型基础上对频率进行改变，如图9所示，可以发现该模型内部所产生的偶极、四极、六极、八极、十极以及十二极等声场局域效应对应的频率随着空心圆柱半径尺寸的增加而减小，即空心圆柱尺寸的变化与产生局域现象所需频率的变化是呈负相关的.不同声学模型在实现同一种声场局域现象时所需要达到的声波频率会随着模型尺寸的增大而减小. 因此，本文提出的此种空心柱状声学微结构可以对SAW芯片进行“按需定制”，根据每个声表面波器件的中心频率来设计实现满足不同需求的SAW微流控芯片.

圆柱由内而外三层半径分为(a)263.20 μm、303.69 μm和323.94 μm;(b)321.13 μm、370.38 μm和395.08 μm;(c)376.50 μm、434.42 μm和463.38 μm;(d)431.20 μm、497.54 μm和530.71 μm

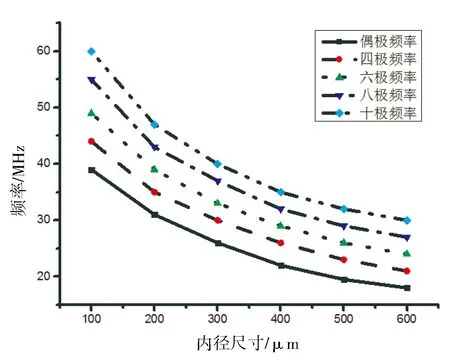
图9 模型尺寸与不同声场局域效果所需频率的关系

总之，由于声场局域效应各个极点的产生都是呈对称分布的，因此这种“声悬浮”效应能够有效禁锢和操纵微粒.如图10模拟了粒子在单焦点、偶极子和四极子声场作用下随时间变化的分布情况.在0 s时刻，粒子均匀分布在圆柱内部，此时内部无任何声场.声波射入模型后，随着时间递增到0.000 15 s和0.000 3 s时刻，可以明显看到由于内部声场的变化，粒子会向能量较高的区域聚集，一定时刻后形成一种动态平衡，使其稳定“禁锢”在强压的正负交界面，达到对微粒的有效操纵.

图10 不同声场局域下的粒子分布图

3 模型理论推导

采用声散射理论进行计算[11-15]，设入射波函数为pin=p0ei(k0rcosφ-wt),其中w为圆频率，k0为波束，i为虚数单位，p0为初始相位.环境声压可以被写为柱面Bessel函数和第一类Hanke函数的形式，入射声压在柱坐标下可以写为：

(1)

模型外、空心圆柱外层、中间层和最内层的声压p0、p1、p2和p3可以分别写为：

(2)

(3)

(4)

其中A和B分别是Bessel和Hankel函数的展开系数，k是波数.另一方面，由于压力值和声速的上升，每个区域的边界都是连续的，因此，边界条件可以表示为：

p0|r=R3=p1|r=R3；vr0|r=R3=vr1|r=R3

(6)

p1|r=R2=p2|r=R2；vr1|r=R2=vr2|r=R2

(7)

p2|r=R1=p3|r=R1；vr2|r=R1=vr3|r=R1

(8)

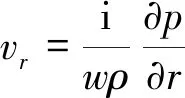
(9)

根据上述矩阵的0阶、1阶、2阶、3阶柱贝塞尔函数和第一类汉克尔函数，分别进行计算，即可得到相对应的单极、偶极、四极、六极和八极现象.

4 结 论

开展了基于双层空心柱状声学微结构的设计，并将该种声学微结构加载在SAW芯片表面，通过微结构间的声波来回作用，不需要特别大的激励信号便可以在芯片表面产生强度很高的声场能量分布.同时，由于基于此种声学微结构的SAW芯片具有很强的调控性，因此可以做到根据实际微粒的尺寸、液体的浓度以及表面波器件的中心频率进行“按需定制”，并为探索和开发性价比更高的声波微流控芯片提供了方向.