基于ARIMA与灰色马尔科夫模型的三亚市交通客流量预测研究*

刘 夏，李苑辉，欧志鹏，陈 磊，陈明锐

(1.三亚航空旅游职业学院,海南 三亚 572000；2.海南大学 计算机与网络空间安全学院,海口 570228)

0 引 言

预测交通客流量的方法较多，国内学者在时间序列方面：孙泗龙(2014)[1]、宋子房(2014)[2]、芮少权(2010)[3]、张嘉成(2016)[4]均构建了时间序列ARIMA模型用于客流量预测，但预测精度仍可提高。在在灰色理论方面：李克昭(2016)构建了优化后的灰色马尔科夫模型[5]，樊冬雪(2015)构建了粒子群无偏灰色马尔科夫链模型[6]，张国帅(2011)将累积法引入到传统灰色马尔科夫模型[7]，杨军(2013)构建基于累积法的灰色马尔科夫模型[8]，朱念(2017)构建灰色马尔科夫模型进行了预测[9]，顾炯(2014)建立基于灰色预测的城市轨道交通短期客流预测模型[10]。此外，曾冬玲(2016)[11]用马尔科夫模型修正灰色模型，预测了云南旅游市场未来3年的客流。汤银英(2018)邵梦汝(2016)、王慧勇(2016)、付建飞(2014)、安然(2015)等学者也从不同的角度将灰色理论分别改进马尔科夫模型[12]、神经网络模型[13]、线性回归模型[14]并用于预测。在国外的研究方面，Liu X(2017)在使用了ARMA、灰色预测GM(1,1)以及ARMA改进回归模型对客流量进行了预测[15]。Xia L(2017)运用灰色预测方法对航线客流量的预测的精确度较高，对航空公司预估客流量和制订销售政策有直接的指导意义[16]。Nieto María Rosa构建了基于ARIMA+GARCH的模型用于客流预测[17]。IslamB将改进的反向传播神经网络与混沌搜索遗传算法和模拟退火算法相结合用于电力预测。

1 数据来源与研究方法描述

1.1 数据来源

选取了三亚市旅游政务网公布的2012—2017每年1月—12月的三亚市旅游统计月度数据，在经过清洗后，选取了来自机场和火车站的客流数据总量作为研究对象。

1.2 研究方法介绍

1.2.1 ARIMA

Box与Jenkins在20世纪70年代首先提出了ARIMA模型。ARIMA模型在时间序列预测方面适用十分广泛，它的全称是自回归积分滑动平均模型[1]。ARIMA(p，d，q)称为差分自回归移动平均模型，AR代表的是自回归，p则为自回归项；MA用于代表移动平均，当中的q则用于表示移动平均的具体项数，字母d则代表时间的序列，即表示移动平均，q代表的是MA移动平均的项数，d表示时间的序列，用于表示在平稳状态下需要进行差分分析的次数。ARIMA模型作为一种回归分析模型，具体是针对非平稳时间序列进行转化，使其变成平稳时间序列，在此基础上分析因变量、随机误差项对应的滞后值以及随现值等。基于原序列的平稳性与回归包括因素角度，能够将ARIMA模型划分成多个过程。

1.2.2 灰色马尔科夫介绍

依据过去的已有探究能够知道，对于灰色预测来讲，遇到那些具备一定规律，同时变化率相对较小的数据序列，其预测的精准度相对较高，然而当遇到那些变化没有规律的数据序列时，很难将其预测的精准度控制在相对较小的范围里。对于马尔科夫链而言，其预测的对象是随机变化的，是一个呈动态变化的系统，对于数据的未来变化趋势是依据当下呈现状态的转移概率来进行推测的，侧面体现了预测结果受每个影响因素所影响的程度，所以，对于那些原始数据起伏变化的系统开展预测，马尔科夫链是最适合的。要想对灰色预测模型具有的缺陷加以弥补，就要把马尔科夫链和其加以整合，充分发挥两者的优势，预测的精准度才能得以大幅提升。灰色马尔科夫模型可以划分成灰色转移状态与灰色转移概率两类模型，所采用的是前者，即灰色转移状态马尔科夫模型，常规而言，它有3个步骤：

第1步，预测状态的划分。

第2步，状态转移概率矩阵的创建，如式(1)与式(2)所示：

(1)

(2)

在式(2)当中：Pij对应的是一步转移概率，其范围在状态i至状态j之间，Mij对应的是一步转移次数，其范围也是在状态i至状态j之间，Mi对应的是状态数量，该数量归属于状态i。

(3)

2 基于ARIMA模型的交通量基础上的拟合

针对以上论述的月旅客数量，运用传统的时间序列模型ARIMA对其加以预测与拟合。

用传统的时间序列ARIMA模型，对上述的每月旅客数进行拟合和预测。要在ARIMA模型创建之前，先做出航线的时序图，得到的结果如图1所示。

图1 每月客流量时序图

根据图1能够获取月旅客量，显示出其季节因素极为显著，每一年旅客数量较少的月份是7、8、9三个月，旅客数量较多的月份在1、2、3三个月。旅客数量的季节调整可运用X-12季节调整法来得以开展，所得到的每月季节指数具体可见表1：

表1 每月季节指数列表

接着对调整后的月旅客数量进行单位根检验，检验的结果如表2所示。

表2 调整之后的旅客数量单位根检验列表

根据表2可得调整后的每月旅客数是一阶单整序列，所以，创建的模型要是ARIMA(p,1,q)模型。

2.1 模型的识别方法

针对NUM具体情况，将其ACF与PACF图画出，识别p和q，得到的结果如图2所示。

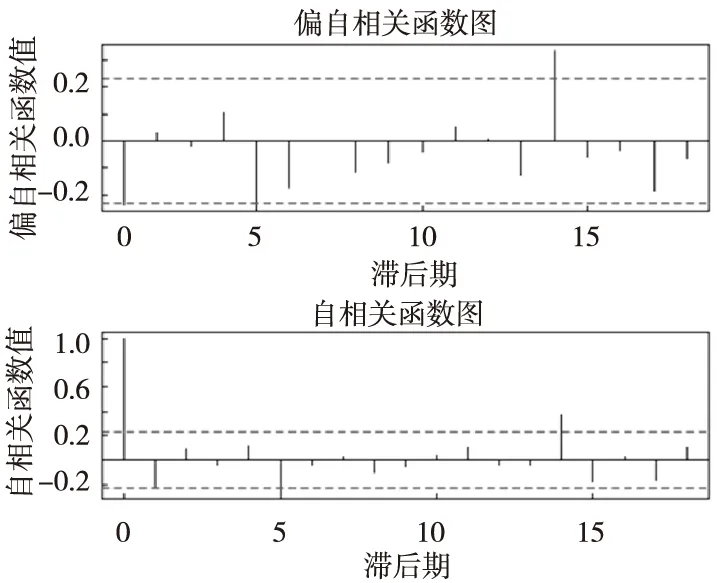
图2 D(passenger_num)的ACF和PACF图

根据图2的ACF和PACF可以得出，D(passenger_num)所对应的PACF图显示出的现象是1期“截尾”，相对于ACF图而言，其显示出的现象则是“拖尾”，结合AIC值最小原则。最后对交通旅客数初步建立ARIMA(1,1,0)。基于多次调试，最后得出和表3显示出的ARIMA(1,1,0)模型的结果。

表3 ARIMA的结果

从表2、表3所提供的数据可知，在0.05的显著水平情况下，模型总似然比检验和ARIMA(1,1,0)的各项系数都是显著的，因此可获得方程：

D(passenger_num)t=189.381 4-

0.919 1D(passenger_num)t-1

(4)

2.2 模型检验

针对以上论述模型的残差加以检验的基础上，将残差的ACF与PACF图画出，对其模型进行观察，看旅客数序列的有效信息有没有全部提取，图3显示的就是所获取的结果：

图3 残差对应的ACF与PACF图

残差序列的ACF和PACF通过图3可知大体都在两个标准差之后，显示出以上所述的模型对序列的全部信息都进行了有效提取。在此基础上，月旅客数可运用所创建的ARIMA(1,1,0)模型加以预测。

2.3 模型的预测

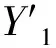
(5)

其中YF1表示每月旅客数的预测序列，Sj表示每月的季节指数。计算预测的平均绝对百分误差。

(6)

按照以上创建的ARIMA(1,1,0)来针对每月交通旅客量进行预测，其MAPE=4.42%。

3 基于灰色马尔科夫模型拟合分析

依照图1可以看出2012—2017年交通旅客量具有明显的季节趋势，采用2012—2017年的每个月拥有的旅客数量作为原始数据，在此基础上创建出灰色马尔科夫预测模型，分组展开预测，这样季节效应对预测所产生的影响就可得以有效规避。

3.1 模型建立

先进行灰色预测，以2012—2017-01的旅客数作为例子建立具体的灰色马尔科夫预测模型。

表4 灰色预测值

第三，对灰色预测的残差进行状态划分，对预测误差进行划分3个不同的状态空间E1，E2，E3，具体划分如下所示：

E1=(36.44,-13.69)，E2=(-13.69,9.07)，E3=(9.07,31.82)

根据上述的划分，可以得出在2012—2017-01月E1状态有1次，E2状态有3次，E3状态有1次。

最后，将预测值计算出来，按照状态的划分，将预测值状态所属残差的组中值取出，然后和以上灰色预测的值进行相加，精准度更高的灰色马尔科夫预测模型的预测值就能够获取。以2012-02的预测值计算为例：

Y=138.448 4+(36.44-13.69)/2=149.82

3.2 模型预测

以此类推可以得到灰色马尔科夫预测模型对2012—2017每年1月—12月的预测值,见表5。

表5 预测值列

根据表5可得，选用灰色马尔科夫模型对2012-01—2017-01预测MAPE=3.70%，灰色预测模型的预测MAPE=8.13%，可知就两者的预测精准度而言，灰色预测模型与灰色马尔科夫模型相比明显落后。因此，应用灰色马尔科夫预测模型针对2012—2017-02-12的交通旅客量进行预测，计算出的MAPE=3.78%。

4 两种模型对比与趋势外预测

4.1 模型对比

比较ARIMA模型与灰色马尔科夫模型对2012-01—2017-12的交通旅客量进行预测，得到的预测时序如图4：

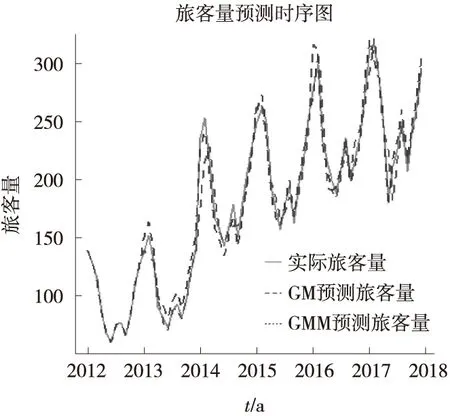
图4 两个模型预测值

并且计算两个模型的预测精度得到的值如表6所示：

表6 两个模型预测精度比较

4.2 趋势外预测

通过上述两种模型的预测精度比较，选用预测精度较好的灰色马尔科夫的模型对2018-01—12月的交通旅客量进行预测。

首先计算2012—2017年每年1月的状态转移概率矩阵：

可以得到2012年1月交通旅客量所处的是E2状态，则初始向量：

得到2018-01的转移概率为

计算得到2018-01的交通旅客量处在E1和E2的状态的概率各为1/2。通过计算可以得到2018-01的交通旅客量为373.260 7万人。根据同样的计算方式得到2018-02-12的交通旅客量如表7。

表7 2018年旅客数的预测

5 结束语

通过使用不同的模型进行建模及分析，在针对不同模型对应的预测精度进行对比之后，最后选择的是灰色马尔科夫预测模型，主要是因为模型的样本预测精准度相对较高，能够对未来一年交通旅客量比较精准加以预测。根据预测情况，可以看出在每年2月作为三亚旅游的旺季，其交通旅客量可能突破400万次，这对当地交通、旅游等部门提前进行工作部署具有重要的意义。灰色马尔科夫模型的方法和结果简单易懂，可以推广到其他相关领域客流量的预测。

从“吃住行游购娱”的旅游六要素来看，交通是决定着一个城市旅游质量的重要因素。与此同时，交通不仅服务于游客，也服务于市民，关乎每一个人的居住舒适度。对于一个常住人口61万的小城，在旅游旺季单月接待超过400万次的游客，对任何一座城市都是一个不小的挑战。因此，三亚应积极在建设外连交通的同时，逐步完善好自己的交通“内动脉”，利用水资源和桥梁建设等手段完成城市交通一体化建设。积极利用数据手段进行实时观测，提前把握客流量的趋势，向交通组织部门和运力部门提前提供科学的数据，充分做到提前部署、提前把控，全面提高交通管理能力。