随机δ冲击下多相关退化的竞争失效可靠性评估*
2019-10-09刘汉葱陶小寒
刘汉葱, 刘 赪**,张 诚,陶小寒
(1.西南交通大学 数学学院统计系,成都611756;2.中铁二局 电务公司,成都 611756)
0 引 言
现代技术的飞速发展使得可靠性理论变得越来越成熟。在20世纪30年代,可靠性的概念最早产生于航空航天领域[1]。1957年发表了《军用电子设备可靠性》的研究报告,该报告为美国军方可靠性的研究指明了方向,成为可靠性领域的重要文件。与此同时,这一报告的发表也标志着可靠性成为一门独立的学科,是可靠性发展的转折点。从20世纪50年代开始,可靠性理论以惊人的速度发展,直至今天,研究者对它各方面的应用积累了丰富的经验。可靠性理论不再单纯地应用到军事方面,它已经从军事方面扩展到了社会经济的各个方面,对经济的发展发挥了一定的作用。随着可靠性理论的日趋成熟,越来越多的数学工具可以解决可靠性问题。
目前,对可靠性的评价指标最常用的是可靠度。除此以外,分布函数、概率密度函数、失效率函数都可作为可靠度的评价指标,且这4者之间相关,后面的内容当中将会有介绍[2]。可靠性评估的方法有退化轨迹法、退化量分布法。退化轨迹法实质上是直接对试验数据进行线性或者非线性的拟合。根据这种方法进行研究的有:Wilson[3]利用该模型分析了一组疲劳裂缝数据的可靠性建模问题;Chen等[4]假设寿命服从特定的分布,根据性能退化数据拟合退化轨迹,得到满足该分布特征的退化轨迹回归系数;Bae等[5]完成了等离子显示器亮度退化数据的可靠性建模。退化轨迹法是一种经验方法,虽然可以快速得到产品性能的退化轨迹,但其操作简单,使得该方法精度较差。同时,因为回归模型法对退化测量误差假设服从的是正态分布,故这种方法难以描述动态的退化过程。退化量分布法指选取合适的分布函数拟合同一测量时间的退化数据,并估计其中的参数,然后用回归分析法拟合与时间相关的参数变化特征。根据这种方法进行研究的有:陈昌等[6]通过最小二乘向量机对某轴承的各性能进行了预测分析;Sun等[7]研究了性能退化服从高斯泊松分布时,预测其寿命。
现从竞争失效的角度出发,针对伴随δ冲击和内部退化的系统,进行可靠性评估。通过Copula相关内容,刻画各退化路径之间的相关性。为了计算上的方便,假设性能退化过程均为线性退化过程,冲击过程为极值冲击模型,且各参数均服从正态分布。最后结合算例分析,证明了模型的可行性和有效性,有很好的工程应用价值。
1 可靠性评价指标及其相互转化关系
可靠度函数:产品的可靠度指产品在规定的时间t内和规定的条件下,完成规定功能的概率,通常用R(t)来表示。

1-F(t),t≥0
失效率函数:产品的失效率函数是指已经工作了t时间没有失效的条件下,在接下来单位时间内失效的概率,记为r(t),则r(t)的定义为
分布函数、概率密度函数、可靠度函数、失效率函数相互唯一确定,其转化关系如下:
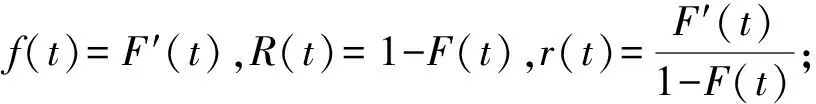

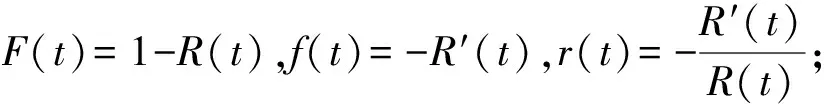

2 伴随δ冲击竞争失效理论及Copula理论
2.1 δ冲击下竞争失效理论
假定系统只存在性能退化失效,但外界存在多个随机冲击,总退化量由两部分构成:系统的连续性能退化导致的退化量(简称内部退化)和每次外界冲击导致系统性能的退化量的突然增加。
为了模型建立的合理性,进行如下假设:
① 系统存在k种性能退化模式,且内部退化过程为线性退化过程;
② 外界存在m种冲击,其到达率为λm的齐次泊松过程;
③ 同一冲击对不同的性能退化造成不同的影响。
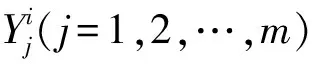
因此系统第l(l=1,2,…,k)种退化模式的总性能退化量为
图1为外界冲击两次间隔时间给定为δ时,竞争失效的图解。
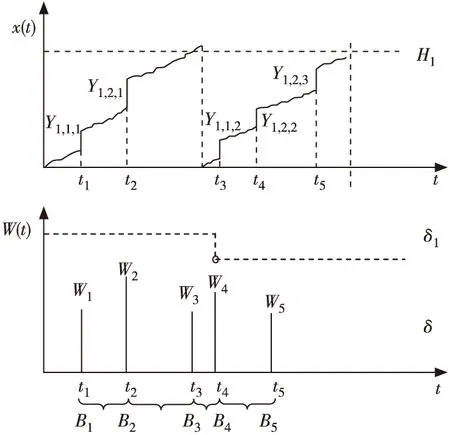
图1 竞争失效图解
2.2 Copula相关理论
定义1[8]n维Copula是一个函数C:[0,1]n→[0,1],且满足:
(1)对于向量u=(u1,u2,…,un),只要u中存在任何分量ui=0,i=1,2,…,n,则
Cn(u)=0
当ui,i≠k,i=1,2,…,n=1,对任意0≤uk≤1,则
Cn(u)=Cn(1,…,1,uk,1,…,1)=uk
(2)对于In中任意由a→b(a的每个分量ai不大于b的对应分量bi)构成的n维盒子,盒子的Copula测度VCn(a,b)≥0,VCn(a,b)实则是从a到b关于Cn的n阶差分。
定理1[8](n维Sklar定理)H(x1,x2,…,xn)是n维随机变量(X1,X2,…,Xn)的联合分布函数,其边际分布分别是F(x1),F(x2),…,F(xn),那么存在唯一的n维Copula函数C(u1,u2,…,un),使得对任意的(x1,x2,…,xn)∈Rn,有:
H(x1,x2,…,xn)=Cθ(F1(x1),F2(x2),…,Fn(xn))
其中:θ是相关程度参数,Cθ解析形式因相关结构各异。
3 基于随机冲击的系统可靠性建模
3.1 相关性失效下伴随单随机冲击、多退化模式下的可靠度模型
假设系统存在k种性能退化模式,伴随一种随机冲击,并且各性能退化之间相互影响,则系统第l(l=1,2,…,k)种性能退化模式的总性能退化量为
当各性能退化模式失效相关时,XS1(t)、XS2(t)、…、XSk(t)不再独立,因此评估任意t时刻的可靠度函数涉及各性能退化模式在t时刻的联合密度函数f(x1,x2,…,xn;t)。由n维Sklar定理,XS1(t)、XS2(t)、…、XSk(t)的联合密度函数为
当然,XS1(t)、XS2(t)、…、XSk(t)的时变相关结构C(u1,u2,…,un;θt)可以通过样本数据统计拟合得到。
因此系统的可靠度函数为
RS(t)=P(XS(t) S1(t) Hk|N(t)=i)P(N(t)=i)= 假设系统存在k种性能退化模式,伴随m种随机冲击,并且各性能退化之间相互影响,则根据上述小结的思想,系统的可靠度函数为 RS(t)=P(XS(t) i1,…,Nm(t)=im)P(N1(t)=i1)…P(Nm(t)=im)= 假设系统有一种冲击两种退化路径,其中冲击均为δ冲击。当外界冲击为δ冲击时,用Bi表示第i(i=1,2,…)次冲击到达时间ti和第i+1次冲击到达时间ti+1之间的间隔,即可得Bi=ti+1-ti,由模型假设可知,Bi为相互独立的随机变量,且服从参数为λ的指数分布。当性能退化量小于L时,其失效阈值为δ1;性能退化量大于L小于H时,其失效阈值为δ2。则在不同失效阈值条件下,系统不发生突发失效的概率为 P(Bi>δk)=exp(-λδk),i=1,2,…;k=1,2 则在t时间内系统的可靠度为 由于R(t|N(t)=i)的计算过于复杂,以下分8种情况进行讨论: (1)系统在(0,t]时间内没有发生外界冲击,可靠度为 R1(t)=R(t|N(t)=0)P(N(t)=0)=P(X1(t)< H1,X2(t) f1(x1)f2(x2)dx1dx2e-λt (2)系统在(0,t]时间内,发生外界冲击等于1次,且两种性能退化量均小于Lp(p=1,2),因系统不可能发生突发失效,则系统可靠度为 L2|N(t)=1)P(N(t)=1)= f1(x1)f2(x2)dx1dx2e-λtλt (3)系统在(0,t]时间内,发生外界冲击等于1次,且第一种性能退化量大于L1小于H1;第二种性能退化量小于L2,因系统不可能发生突发失效,则系统可靠度为 X2(t)+S2(t) P(N(t)=1)= f1(x1)f2(x2)dx1dx2e-λtλt (4)系统在(0,t]时间内,第一种性能退化小于L1,第二种性能退化量大于L2小于H2,与第三种情况类似,则系统可靠度为 X1(t)+S1(t) f1(x1)f2(x2)dx1dx2e-λtλt X2(t)+S2(t) exp(-iλδ1)P(N(t)=i)= P(N(u)=k,N(t-u)=j)=P(N(u)=k)P(N(t-u)= S1(t) exp(-kλδ1)exp(-jλδ2)P(N(t)=i)= f1(x1)f2(x2)dx1dx2duexp(-kλδ1)exp(-jλδ2) (7)系统在(0,t]时间内,发生外界冲击大于等于1次,且第一种性能退化量小于L1,第二种性能退化量大于L1小于H1,则系统可靠度的计算类似于6),可靠度为 S2(t) exp(-kλδ1)exp(-jλδ2)P(N(t)=i)= f1(x1)f2(x2)dx1dx2du (8)系统在(0,t]时间内,发生外界冲击大于等于1次,且两种性能退化量均大于Hq(q=1,2),则系统的可靠度函数为 H2|N(t)=i)Rs(t|N(t)=i)P(N(t)=i) P(N(u1)=k1,N(t-u1)=j1)= P(N(u1)=k1)P(N(t-u1)=j1)= P(N(u2)=k2,N(t-u2)=j2)= P(N(u2)=k2)P(N(t-u2)=j2)= 令FX1(k1,L1,t)表示在外界冲击次数为N(t)=k1且第一种退化性能退化量小于L1的分布函数;FX2(k2,L2,t)表示在外界冲击次数为N(t)=k2且第一种退化性能退化量小于L2的分布函数,则 FX1(k1,L1,t)=P(X1(t)+S1(t) FX2(k2,L2,t)=P(X2(t)+S2(t) 故其密度函数为 由此可得 f1(x1)f2(x2)du1du2dx1dx2 系统在运行到时刻t时,其状态是上述8种状态之一,且它们为互斥事件,因此系统在时刻t时的可靠度为上述8种之和,由此可得: R(t)=R1(t)+R2(t)+R3(t)+R4(t)+R5(t)+ R6(t)+R7(t)+R8(t) (1) 基于微电子机械系统疲劳机制,这些研究中强调的微电子机械系统器件是Sandia开发的微型发动机,其正交静电线性制动器连接到轮毂上的齿轮。齿轮主要失效机理是接触区域的磨损,还使用滑动梁上试验结构来测量不同表面涂层和环境的摩擦系数和磨损形态。其参数如表1所示 表1 系统可靠度参数值 将表1中的值代入式(1),得到了微电子的可靠性曲线(图1)。 图2 微电子产品的可靠度函数 从上述的可靠度曲线可得到如下的结论:第Ⅰ条曲线表示第一种退化路径下的可靠度退化曲线;第Ⅱ条曲线表示第二种退化路径下的可靠度曲线;第Ⅲ条曲线表示当两者退化相关时,系统的可靠度曲线。可以发现,当两者相关时,系统的可靠度有所下降,反映了有冲击情形下,两种退化相互影响。当要求某一产品或者系统的可靠度达到某一固定值时,从可靠度曲线就可以得到产品退出市场的时间,或者系统需要维修的时间。这对于产品或者系统的后期维修有着重要的意义。 对系统经历性能退化和外界冲击过程造成的退化,建立了竞争失效可靠性模型。通过案例分析,验证了模型的合理性和有效性。 在线性退化轨迹下,给出了一般情形下系统可靠性表达的解析式;通过时变Copula选择方法,得到了相关性退化、δ冲击下系统可靠度的表达式,并具体给出了两种退化路径,一种δ冲击下的可靠度函数表达式;在给定参数下,得到了微电子机械产品的可靠度曲线。 但只考虑了退化过程为线性退化,冲击为δ冲击下系统的可靠度函数。在后续的研究中可以考虑多冲击,其他形式退化过程下,系统竞争失效的可靠性建模。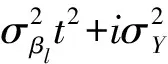
3.2 相关性失效下伴随多随机冲击、多退化模式下的可靠度模型
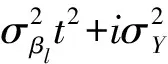
4 基于δ冲击下的系统可靠性建模
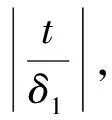
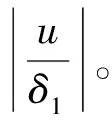

5 案例分析


6 总 结
